Binomial Identities Expansion of a n x a

Binomial Identities

Expansion of (a + n x) • (a + x) = a + x = 1 C 0 a + 1 C 1 x • (a + x) = aa + ax + xa + xx = x 2 + 2 ax + a 2 = 2 + C ax + C a 2 C x 2 0 2 1 2 2 • The 4 red terms are the “formal” expansion of (a+x)2 • The 3 blue terms are the “simplified” expansion of (a+x)2 • (a + x)(a + x) = aaa + aax + axa + axx + xaa + xax + xxa + xxx = x 3 + 3 a 2 x + 3 ax 2 + a 3 = 3 + C a 2 x + C ax 2 + C a 3 C x 3 0 3 1 3 2 3 3

Generalizing. . . • In (a + x)4, how many terms does the: • formal expansion have? • simplified expansion have? • In (a + x)n, how many terms does the: • formal expansion have? • simplified expansion have?

The Coefficient on k n-k ax • The coefficient on akxn-k is the number of terms in the formal expansion that have exactly k as (and hence exactly n-k xs). • It is equal to the number of ways of choosing an a from exactly k of the n binomial factors: n. Ck.

Binomial Theorem • (1 + x)n = n. C 0 x 0 + n. C 1 x 1 + n. C 2 x 2 +. . . n. Cnxn • In addition to the combinatorial argument that the coefficient of xi is n. Ci, we can prove this theorem by induction on n.

Binomial Identities • n. Ck = n!/[k!(n-k)!] = n. Cn-k The number of ways to pick k objects from n = the ways to pick not pick k (i. e. , to pick n-k). • Pascal’s identity: n. Ck = n-1 Ck + n-1 Ck-1 • The number of ways to pick k objects from n can be partitioned into 2 parts: • Those that exclude a particular object i: n-1 Ck • Those that include object i: n-1 Ck-1 • Give an algebraic proof of this identity.

n. Ck k. Cm = n. Cm n-m. Ck-m • Each side of the equation counts the number of k-subsets with an m-subsubset. • The LHS counts: 1. Pick k objects from n: n. Ck 2. Pick m special objects from the k: k. Cm • The RHS counts: 1. Pick m special objects that will be part of the ksubset: n. Cm 2. Pick the k-m non-special objects: n-m. Ck-m

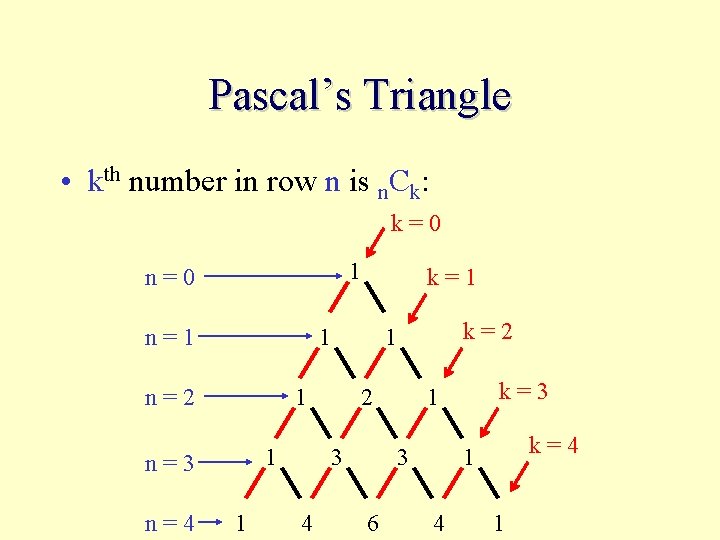
Pascal’s Triangle • kth number in row n is n. Ck: k=0 1 n=0 n=1 1 n=2 1 1 2 3 4 k=2 1 1 n=3 n=4 k=1 3 6 k=3 1 k=4 1

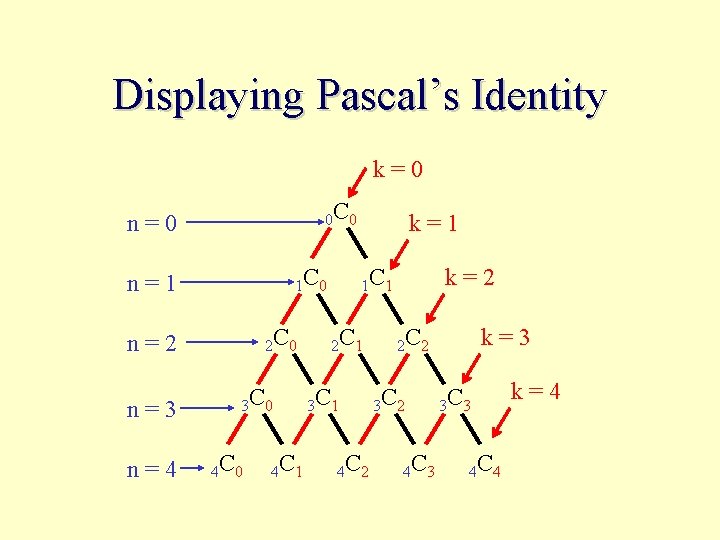
Displaying Pascal’s Identity k=0 0 C 0 n=0 1 C 0 n=1 2 C 0 n=2 n=3 n=4 3 C 0 4 C 1 k=1 1 C 1 2 C 1 3 C 1 4 C 2 k=2 2 C 2 3 C 2 4 C 3 k=3 3 C 3 4 C 4 k=4

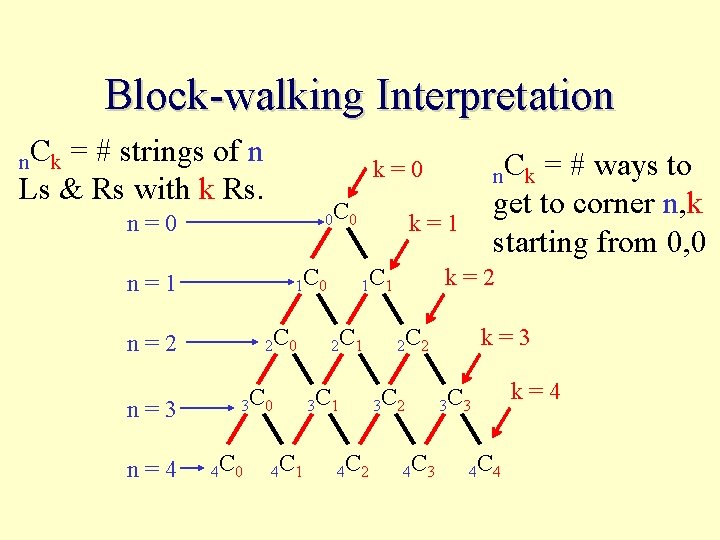
Block-walking Interpretation n. Ck = # strings of n Ls & Rs with k Rs. 0 C 0 n=0 1 C 0 n=1 2 C 0 n=2 n=3 n=4 3 C 0 4 C 0 n. Ck = # ways to get to corner n, k starting from 0, 0 k=0 4 C 1 k=1 1 C 1 2 C 1 3 C 1 4 C 2 k=2 2 C 2 3 C 2 4 C 3 k=3 3 C 3 4 C 4 k=4

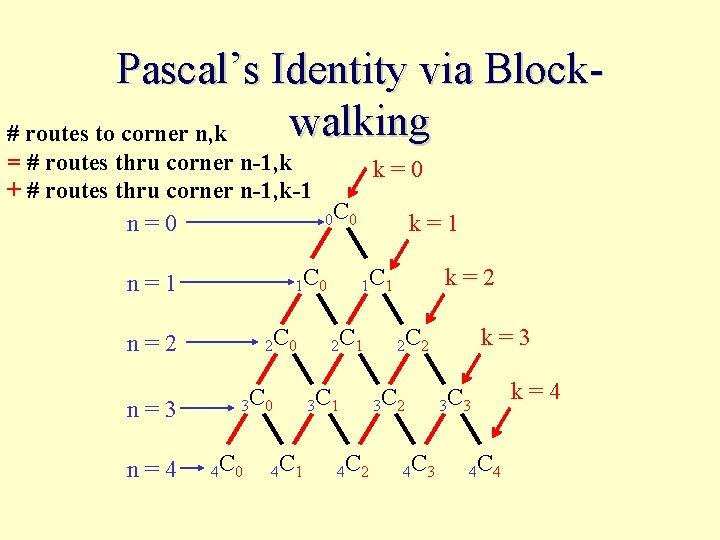
Pascal’s Identity via Blockwalking # routes to corner n, k = # routes thru corner n-1, k k=0 + # routes thru corner n-1, k-1 0 C 0 n=0 k=1 1 C 0 n=1 2 C 0 n=2 n=3 n=4 3 C 0 4 C 1 1 C 1 2 C 1 3 C 1 4 C 2 k=2 2 C 2 3 C 2 4 C 3 k=3 3 C 3 4 C 4 k=4

n. C 0 + n. C 1 + n. C 2 +. . . + n. Cn = n 2 • LHS counts # subsets of n elements using the sum rule: partitioning the subsets according to their size (k value). • RHS counts # subsets of n elements using the product rule: • Is element 1 in subset? (2 choices) • Is element 2 in subset? (2 choices) … • Is element n in subset? (2 choices)

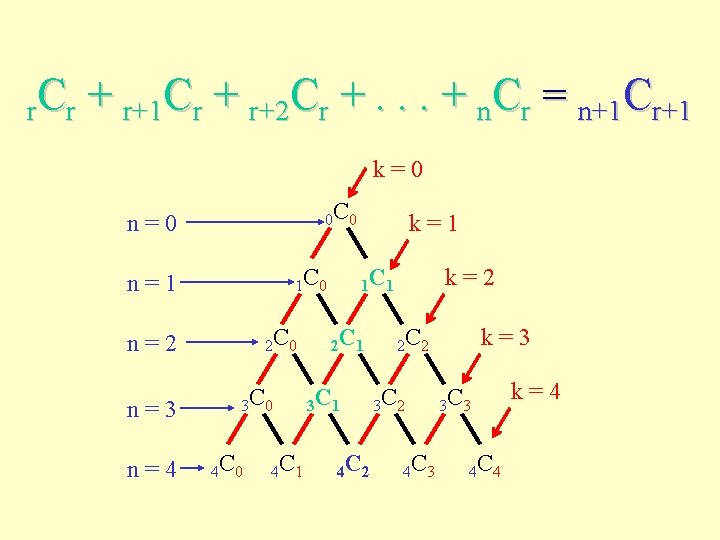
r. C r + r+1 Cr + r+2 Cr +. . . + n. Cr = n+1 Cr+1 k=0 0 C 0 n=0 1 C 0 n=1 2 C 0 n=2 n=3 n=4 3 C 0 4 C 1 k=1 1 C 1 2 C 1 3 C 1 4 C 2 k=2 2 C 2 3 C 2 4 C 3 k=3 3 C 3 4 C 4 k=4

r. C r + r+1 Cr + r+2 Cr +. . . + n. Cr = n+1 Cr+1 • RHS = routes to corner 4, 2 • LHS: Partition the routes to 4, 2 into those: • whose last right branch is at corner 1, 1: 1 C 1 • whose last right branch is at corner 2, 1: 2 C 1 • whose last right branch is at corner 3, 1: 3 C 1 • For each subset of routes, there is only 1 way to complete the route from that corner to 4, 2: RLL, RL, & R respectively. • The identity generalizes this argument.

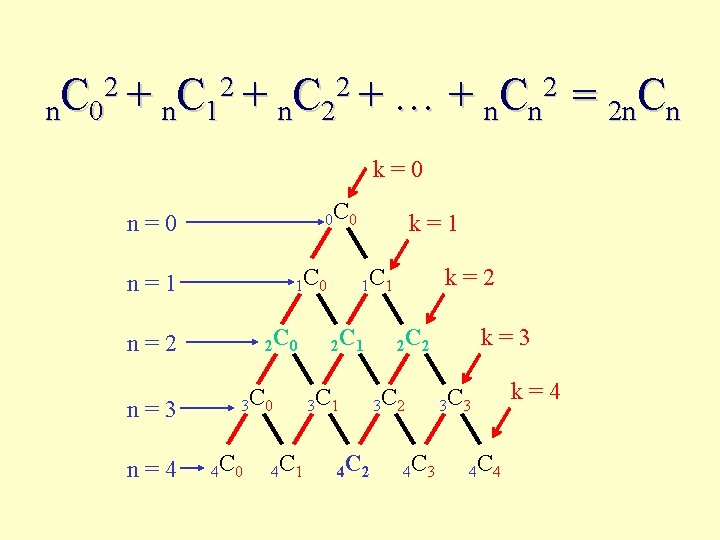
2 2 2 n. C 0 + n C 1 + n C 2 + …+ 2 n. Cn k=0 0 C 0 n=0 1 C 0 n=1 2 C 0 n=2 n=3 n=4 3 C 0 4 C 1 k=1 1 C 1 2 C 1 3 C 1 4 C 2 k=2 2 C 2 3 C 2 4 C 3 k=3 3 C 3 4 C 4 k=4 = 2 n. Cn

2 2 2 n. C 0 + n C 1 + n C 2 + …+ 2 n. Cn = 2 n. Cn • RHS = all routes to corner 4, 2 • LHS partitions routes to 4, 2 into those that: • go thru corner 2, 0: 2 C 0 2 C 2 • go thru corner 2, 1: 2 C 1 • go thru corner 2, 2: 2 C 2 2 C 0 • The identity generalizes this argument: • # routes to 2 n, n that go thru n, k = n. Ck n. Cn-k • Sum over k = 0 to n

1 2 3 + 2 3 4 + 3 4 5 +…+ (n-2) (n-1) n = ? • The general term = (k-2)(k-1)k = P(k, 3) = k!/(k-3)! = 3! k. C 3 • Sum = 3!3 C 3 + 3!4 C 3 + 3!5 C 3 +. . . + 3!n. C 3 = 3! [3 C 3 + 4 C 3 + 5 C 3 +. . . + n. C 3 ] = 3! n+1 C 4

A Strategy • When the general term of a sum is not a binomial coefficient: • break it into a sum of P(n, k) terms, if possible; • rewrite these terms using binomial coefficients

• 12 + 22 + 32 +. . . + n 2 = ? • General term: = k 2 = k(k-1) + k = P(k, 2) + k = 2! k. C 2 + k

• Sum Σk=1, n (2! k. C 2 + k ) = 2! Σk=1, n k. C 2 + Σk=1, n k = 2! n+1 C 3 + n+1 C 2

Another Strategy: Manipulate the Binomial Theorem • (1 + 1)n = 2 n = n. C 0 + n. C 1 +. . . + n. Cn • (1 - 1)n = 0 = n. C 0 - n. C 1 + n. C 2 -. . . +(-1)n n. Cn or n-1 C + C. . . = C +. . . = 2 n 0 n 2 n 1 n 3 • Differentiate the Binomial theorem, • n(1 + x)n-1 = 1 n. C 1 x 0 + 2 n. C 2 x 1 + 3 n. C 3 x 2 + … + nn. Cnxn-1 • n(1 + 1)n-1 = 1 n. C 1 + 2 n. C 2 + 3 n. C 3 + … + nn. Cn