Binomial Distribution n What the binomial distribution is

Binomial Distribution n. What the binomial distribution is n. How to recognise situations where the binomial distribution applies n. How to find probabilities for a given binomial distribution, by calculation and from tables

When to use the binomial distribution n Independent variables

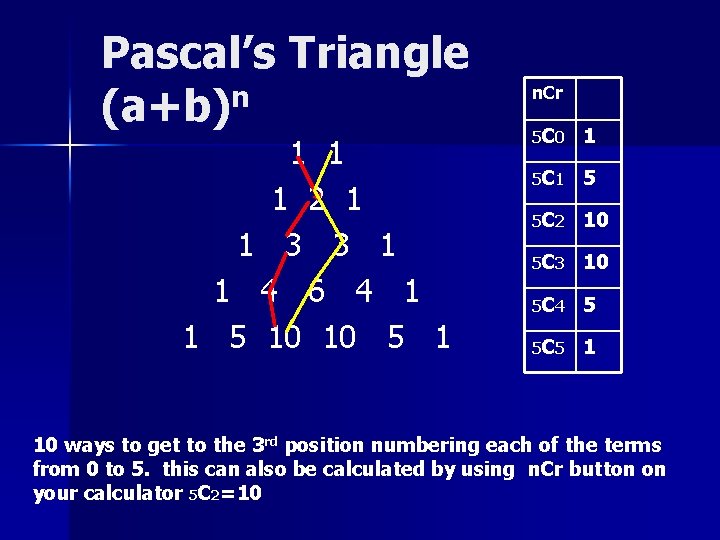
Pascal’s Triangle n (a+b) 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 n. Cr 5 C 0 1 5 C 1 5 5 C 2 10 5 C 3 10 5 C 4 5 5 C 5 1 10 ways to get to the 3 rd position numbering each of the terms from 0 to 5. this can also be calculated by using n. Cr button on your calculator 5 C 2=10

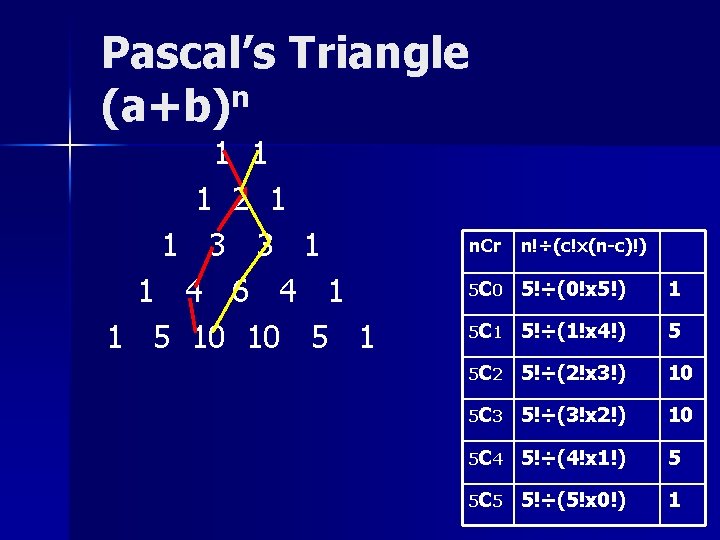
Pascal’s Triangle n (a+b) 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 n. Cr n!÷(c!x(n-c)!) 5 C 0 5!÷(0!x 5!) 1 5 C 1 5!÷(1!x 4!) 5 5 C 2 5!÷(2!x 3!) 10 5 C 3 5!÷(3!x 2!) 10 5 C 4 5!÷(4!x 1!) 5 5 C 5 5!÷(5!x 0!) 1

A coin is tossed 7 times. Find the probability of getting exactly 3 heads. We could do Pascal's triangle or we could calculate: 7 C 3 x (P(H))7 The probability of getting a head is ½

TASK n Exercise A Page 61

Unequal Probabilities A dice is rolled 5 times n What is the probability it will show 6 exactly 3 times? n P(6’)=5/6 P(6)=1/6

Task / Homework n Exercise B Page 62

The Binomial distribution is all about success and failure. When to use the Binomial Distribution – – A fixed number of trials Only two outcomes – – (true, false; heads tails; girl, boy; six, not six …. . ) Each trial is independent IF the random variable X has Binomial distribution, then we write X B(n, p)

Sometimes you have to use the Binomial Formula

Eggs are packed in boxes of 12. The probability that each egg is broken is 0. 35 Find the probability in a random box of eggs: there are 4 broken eggs

Task / homework n Exercise C Page 65

Eggs are packed in boxes of 12. The probability that each egg is broken is 0. 35 Find the probability in a random box of eggs: There are less than 3 broken eggs

USING TABLES of the Binomial distribution An easier way to add up binomial probabilities is to use the cumulative binomial tables Find the probability of getting 3 successes in 6 trials, when n=6 and p=0. 3 n=6 x 0 P=0. 3 P(X=x) 0. 1176 1 2 3 4 5 6 0. 4202 0. 7443 0. 9295 0. 9891 0. 9993 1. 000

n=6 x 0 1 2 3 4 5 6 P=0. 3 P(X=x) 0. 1176 0. 4202 0. 7443 0. 9295 0. 9891 0. 9993 1. 000 http: //assets. cambridge. org/97805216/05397/excerpt/9780521605397_excerpt. pdf The probability of getting 3 or fewer successes is found by adding: P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0. 1176 + 0. 3026 + 0. 3241 + 0. 1852 = 0. 9295 This is a cumulative probability.

Task / homework n Exercise D page 67

Mean variance and standard deviation n μ = Σx x P(X=x)=mean n This is the description of how to get the mean of a discrete and random variable defined in previous chapter. n The mean of a random variable whos distribution is B(n, p) is given as: nμ =np

Mean, n variance & standard deviation σ²=Σx² x P(X=x) - μ² n is the definition of variance, from the last chapter of a discrete random variable. n The variance of a random variable whose distribution is B(n, p) n σ²= n σ= np(1 -p)

TASK / HOMEWORK Exercise E n Mixed Questions n Test Your self n