BINMIO DE NEWTON PROFESSOR keyson Gondim Binmio de

BINÔMIO DE NEWTON PROFESSOR: keyson Gondim

Binômio de Newton Isaac Newton nasceu na pequena cidade inglesa de Lincolnshire em 4 de janeiro de 1643 e morreu em 31 de março de 1727. Ele foi um menino rebelde, mas você também seria se sua mãe o abandonasse em um colégio interno que ensinava gramática na maior parte do tempo. . . Essa não era a disciplina preferida do jovem Newton, que, como vamos ver, desenvolveu várias teorias que revolucionaram a matemática, física e astronomia. Em Cambridge, Isaac Newton foi o primeiro da classe. Formou-se em 1665 e teve que retornar a sua aldeia natal quando a universidade fechou devido ao surto de peste bubônica. Como a epidemia o impedia de sair de casa, o jovem se dedicou a rever tudo o que tinha aprendido na faculdade. A partir daí, ele não parou de pesquisar e realizar experimentos. Nessa época, Newton dava os primeiros passos rumo às descobertas mais importantes, como a decomposição da luz, o princípio da gravitação universal, desenvolvimentos matemáticos diversos e as chamadas três leis de Newton.

Binômio de Newton 3. 1 - Definição Denomina-se Binômio de Newton, a todo binômio da forma (a + b)n, sendo n um número natural, que é chamado de ordem do binômio. Expansão de alguns Binômios: (a + b)0 = 1 (a + b)1 = 1. a + 1. b (a + b)2 = 1. a 2 + 2. a. b + 1. b 2 (a + b)3 = 1. a 3 + 3. a 2. b + 3. a. b 2 + 1. b 3 (a + b)4 = 1. a 4 + 4. a 3. b + 6. a 2. b 2 + 4. a. b 3 + 1. b 4 (a + b)5 = 1. a 5 + 5. a 4. b + 10. a 3. b 2 + 10. a 2. b 3 + 5. a. b 4 + 1. b 5 (a + b)6 = 1. a 6 + 6. a 5. b + 15. a 4. b 2 + 20. a 3. b 3 + 15. a 2. b 4 + 6. a. b 5 + 1. b 6

Binômio de Newton Para expandir uma equação binomial, pode-se seguir os passos: 01. Todos os membros terão o termo a e, também, o b. (Ou seja, deve existir o termo a. b em todos os termos). 02. No primeiro termo atribui-se ao expoente de a o valor n e ao expoente de b o valor 0. A seguir diminui-se de 1 o valor do expoente de a e aumenta-se de 1 o valor do expoente de b. Continua-se até o último termo que deve ter o valor 0 no expoente de a e o valor n no expoente de b. 03. A soma dos expoentes de cada termo deve ser igual ao expoente do binômio. 04. Os valores numéricos em cada termo, são chamados de coeficientes binomiais, e são retirados do TRI NGULO DE PASCAL

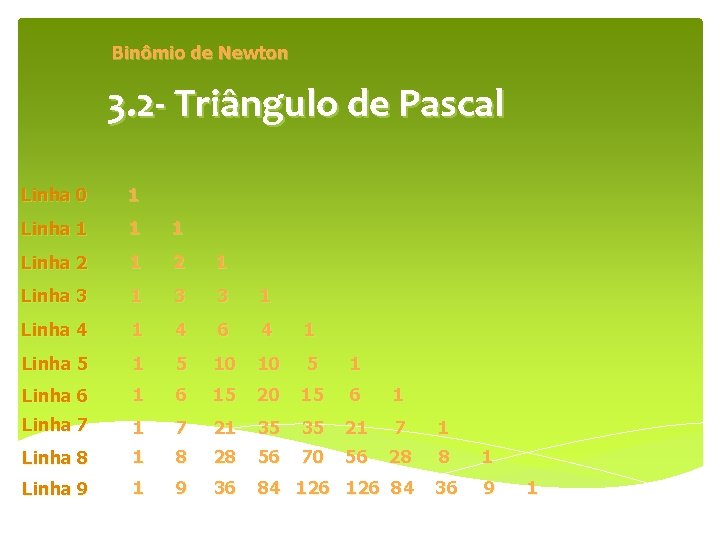
Binômio de Newton 3. 2 - Triângulo de Pascal Linha 0 1 Linha 1 1 1 Linha 2 1 Linha 3 1 3 3 1 Linha 4 1 4 6 4 1 Linha 5 10 10 5 1 Linha 6 15 20 15 6 1 Linha 7 1 7 21 35 35 21 7 1 Linha 8 1 8 28 56 70 56 28 8 1 Linha 9 1 9 36 84 126 84 36 9 1

Propriedades do triângulo de pascal P 1: Em qualquer linha, dois números binomiais equidistantes dos extremos são iguais. Esses binomiais são complementares.

Propriedades do triângulo de Pascal P 2: Teorema das linhas: A soma dos elementos da enésima linha é 2 n.

Propriedades do triângulo de Pascal P 3: Teorema das colunas: A soma dos elementos de qualquer coluna, do 1º elemento até qualquer outro é igual ao elemento situado na coluna à direita da considerada e na linha imediatamente abaixo. Se n ≥ p, , sendo n e p naturais. No caso dos exemplos, temos: i) ii)

Propriedades do triângulo de Pascal P 4: Teorema das diagonais: A soma dos elementos situados na mesma diagonal desde o elemento da 1ª coluna até o de outra qualquer é igual ao elemento imediatamente abaixo deste. Se n ≥ p, sendo n e p naturais. No caso do exemplo, temos:

Binômio de Newton 3. 3 - Exemplos Qual é o termo em x 5 no desenvolvimento de (x + 3)8 ?

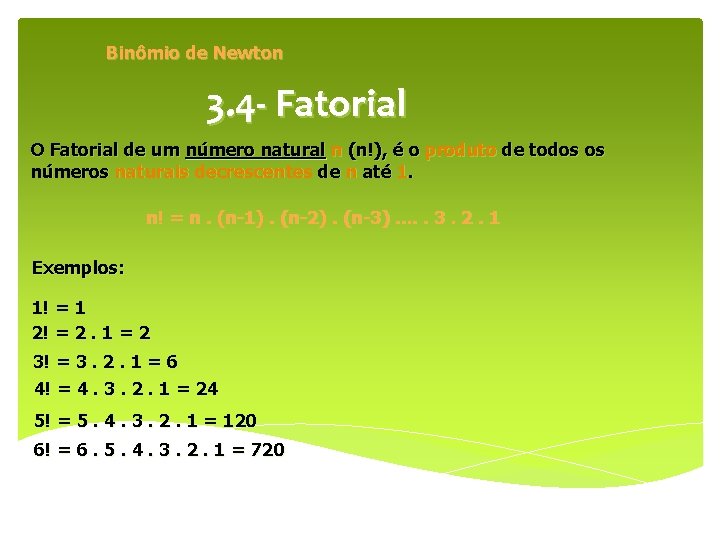
Binômio de Newton 3. 4 - Fatorial O Fatorial de um número natural n (n!), é o produto de todos os números naturais decrescentes de n até 1. n! = n. (n-1). (n-2). (n-3). . . 3. 2. 1 Exemplos: 1! = 1 2! = 2. 1 = 2 3! = 3. 2. 1 = 6 4! = 4. 3. 2. 1 = 24 5! = 5. 4. 3. 2. 1 = 120 6! = 6. 5. 4. 3. 2. 1 = 720

Binômio de Newton 3. 5 - Termo Geral do Binômio Um termo genérico do desenvolvimento de (a+b)n , sendo p um número natural, é dado por: Onde: é denominado Número Binomial

Números binomiais

Binomiais complementares:

Números binomiais igualdades

Números binomiais relação de Sti. Fel

Soma dos coeficientes de um Binômio de Newton Basta substituir qualquer variável por 1