Binary Trees CS 1316 Representing Structure and Behavior

Binary Trees CS 1316: Representing Structure and Behavior

Story l l Binary Trees Structuring Binary Trees to make them fast for searching • • l l Binary search trees How we insert() in order, how we traverse in order, how we search in order More than one way to traverse: Pre-order Treating a tree like a list

Here’s the question l l Searching a list and an array is O(n) We can arrange an array so that searching it is O(log n) • Binary search of an ordered array. l l Lists are harder to arrange to create a faster search. How about trees?

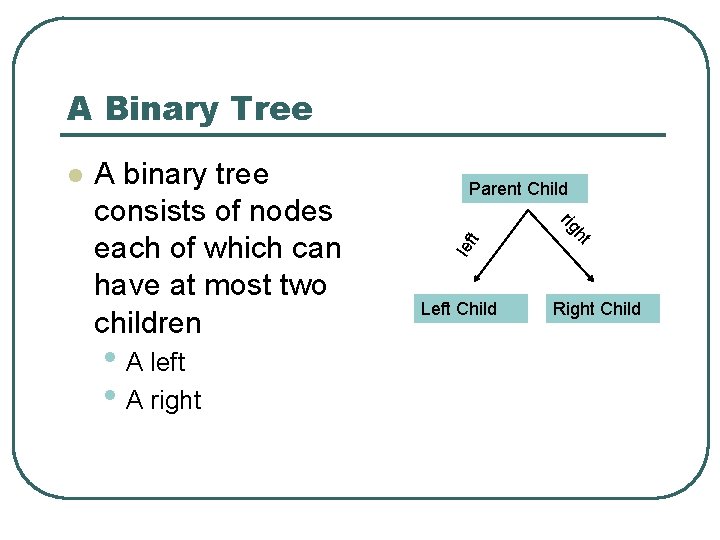
A Binary Tree t Left Child ht • A left • A right Parent Child rig A binary tree consists of nodes each of which can have at most two children lef l Right Child

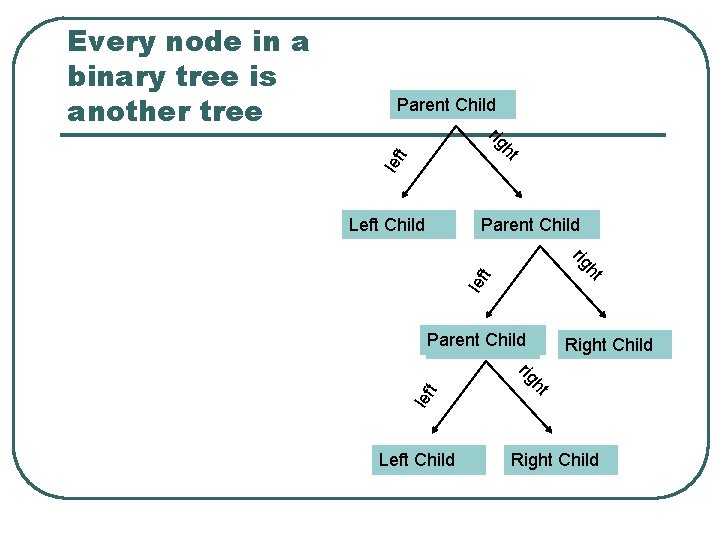
Parent Child t ht rig lef Left Child Right Child Parent Child lef t ht rig Parent Child Left Child Right Child Left Child ht t rig lef Every node in a binary tree is another tree Right Child

Computer scientists know a lot about binary trees l For example, how many levels will you have for n nodes in a binary tree? • Maximum: n • Minimum: 1+ log n

Defining a binary tree public class Tree. Node { private String data; private Tree. Node left; private Tree. Node right; public Tree. Node(String something){ data = something; left = null; right = null; } Our nodes will contain Strings as their data. Could be anything.

Accessors // Accessors public String get. Data() {return data; } public void set. Data(String something){data = something; } public Tree. Node get. Left() {return left; } public Tree. Node get. Right() {return right; } public void set. Left(Tree. Node newleft){left = newleft; } public void set. Right(Tree. Node newright){right = newright; }

Defining printing on a node (for a tree, recursively) public String to. String() {return "This: "+this. get. Data()+ " Left: "+this. get. Left() + " Right: "+this. get. Right(); }

Testing the printing > Tree. Node node 1 = new Tree. Node("george"); > node 1 This: george Left: null Right: null > Tree. Node node 1 b = new Tree. Node("alvin") > node 1. set. Left(node 1 b) > node 1 This: george Left: This: alvin Left: null Right: null

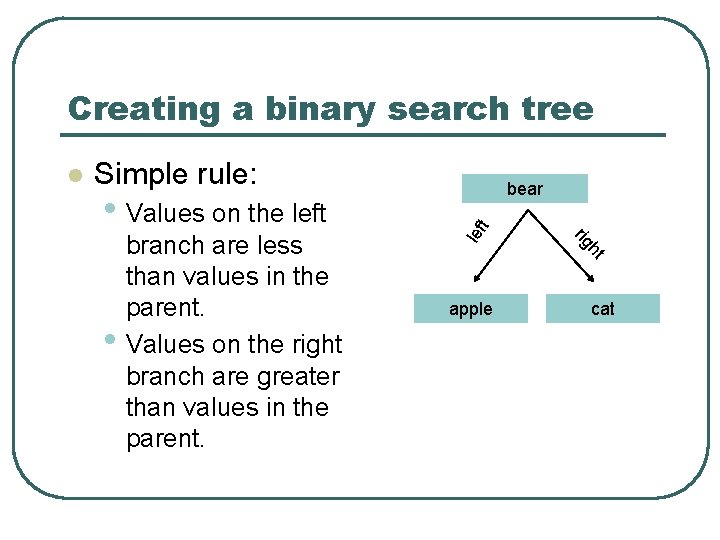
Creating a binary search tree Simple rule: ht rig • branch are less than values in the parent. Values on the right branch are greater than values in the parent. t • Values on the left bear lef l apple cat

Inserting in order in a binary tree l Is the value to insert less than the current node’s value? • • l Does the left branch have a node already? If not, put it there. If so, insert it on the left. The value to insert must be greater than or equal to the current node’s value. • • Does the right branch have a node already? If not, put it there. If so, insert it on the right.

How we compare strings > "abc". compare. To("abc") 0 > "abc". compare. To("aaa") 1 > "abc". compare. To("bbb") -1 > "bear". compare. To("bear") 0 > "bear". compare. To("beat") -2

Code // Insert in order public void insert(Tree. Node new. One){ if (this. data. compare. To(new. One. data) > 0){ if (this. get. Left() == null) {this. set. Left(new. One); } else {this. get. Left(). insert(new. One); }} else { if (this. get. Right() == null) {this. set. Right(new. One); } else {this. get. Right(). insert(new. One); } } }

Testing > Tree. Node node 1 = new Tree. Node("george"); > Tree. Node node 2 = new Tree. Node("betty"); > Tree. Node node 3 = new Tree. Node("joseph"); > Tree. Node node 4 = new Tree. Node("zach"); > node 1 This: george Left: null Right: null > node 1. insert(node 2) > node 1 This: george Left: This: betty Left: null Right: null

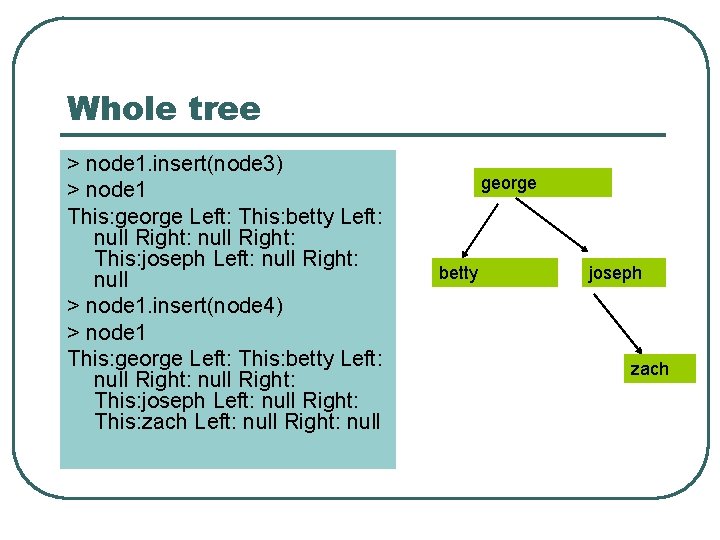
Whole tree > node 1. insert(node 3) > node 1 This: george Left: This: betty Left: null Right: This: joseph Left: null Right: null > node 1. insert(node 4) > node 1 This: george Left: This: betty Left: null Right: This: joseph Left: null Right: This: zach Left: null Right: null george betty joseph zach

How do we find things here? l Given something to find: • Is it me? If so, return me. • Is it less than me? • Is the left null? If so, give up. • If not, search the left. • Otherwise • Is the right null? If so, give up. • If not, search the right.

Code public Tree. Node find(String some. Value){ if (this. get. Data(). compare. To(some. Value) == 0) {return this; } if (this. data. compare. To(some. Value) > 0){ if (this. get. Left() == null) {return null; } else {return this. get. Left(). find(some. Value); }} else { if (this. get. Right() == null) {return null; } else {return this. get. Right(). find(some. Value); }} }

Testing > node 1. find("betty") This: betty Left: null Right: null > node 1. find("mark") null

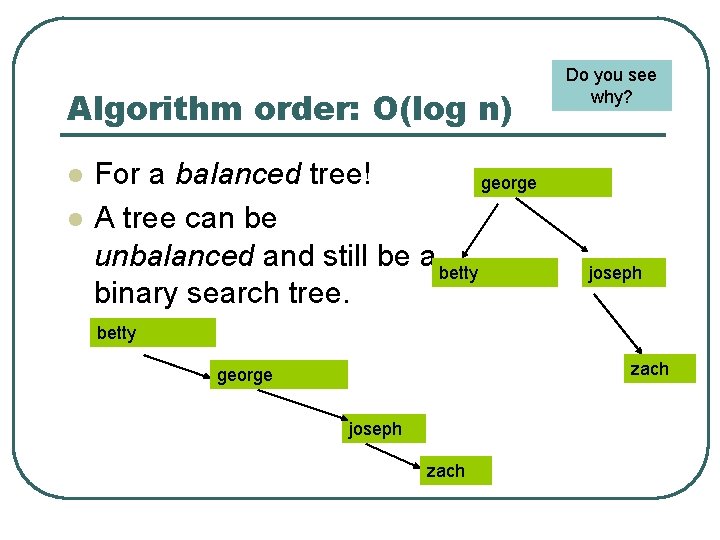
Algorithm order: O(log n) l l For a balanced tree! george A tree can be unbalanced and still be a betty binary search tree. Do you see why? joseph betty zach george joseph zach

How do we print a tree in order? l Is there a left node? l Print me Is there a right node? l • Print the left • Print the right

Code //In-Order Traversal public String traverse(){ String return. Value = ""; // Visit left if (this. get. Left() != null) {return. Value += " "+this. get. Left(). traverse(); } // Visit me return. Value += " "+this. get. Data(); // Visit right if (this. get. Right() != null) {return. Value += " "+this. get. Right(). traverse(); } return. Value; } > node 1. traverse() " betty george joseph zach"

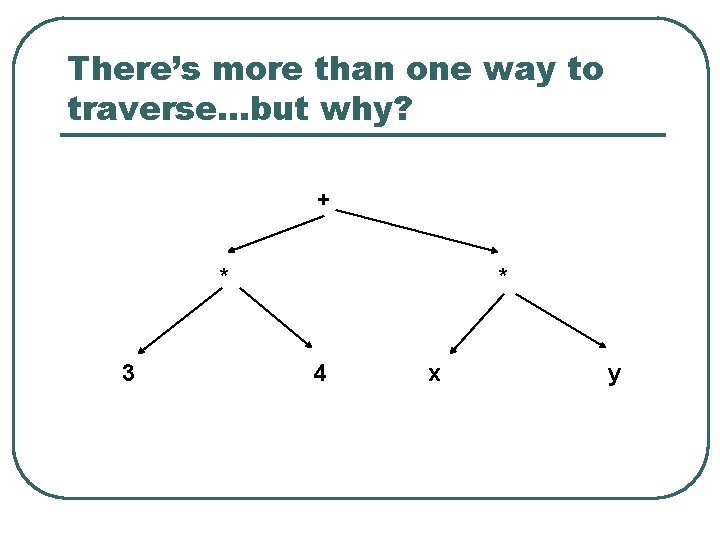
There’s more than one way to traverse…but why? + * 3 * 4 x y

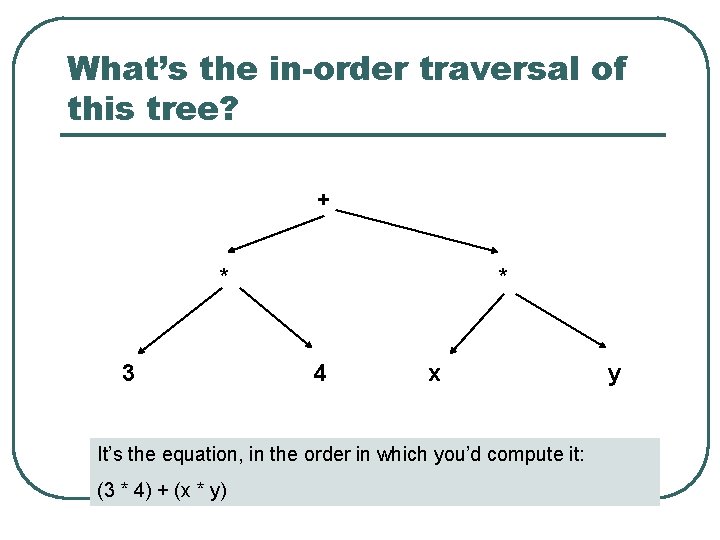
What’s the in-order traversal of this tree? + * 3 * 4 x It’s the equation, in the order in which you’d compute it: (3 * 4) + (x * y) y

Another traversal: Post-order l Is there a left node? l Is there a right node? l Print me • Print the left • Print the right

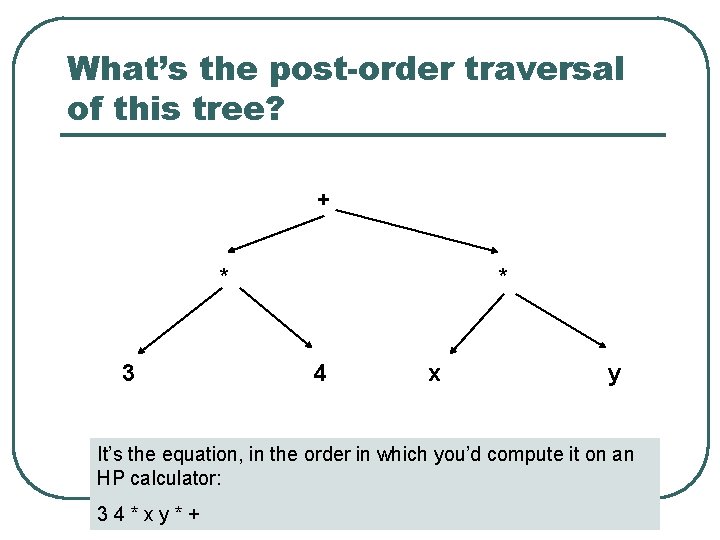
What’s the post-order traversal of this tree? + * 3 * 4 x y It’s the equation, in the order in which you’d compute it on an HP calculator: 34*xy*+

So what’s the big deal? l Binary trees are cute. • Easy to do useful things with them. • Searching quickly. • Using them to evaluate equations. • Operations are easily written small and • l recursively. We know interesting facts about them. Is that all? • Turns out that binary trees can do ANYTHING

Binary trees can represent anything! l l We can map an n-ary tree (like a scene graph) to a binary tree. We can use a binary tree to represent a list. • How about the ability to add to the first and to the last, like our lists?

add. First() and add. Last() public void add. First(Tree. Node new. One){ if (this. get. Left() == null) {this. set. Left(new. One); } else {this. get. Left(). add. First(new. One); } } public void add. Last(Tree. Node new. One){ if (this. get. Right() == null) {this. set. Right(new. One); } else {this. get. Right(). add. Last(new. One); } }

Playing it out > Tree. Node node 1 = new Tree. Node("the") > node 1. add. First(new Tree. Node("George of")) > node 1. add. Last(new Tree. Node("jungle")) > node 1. traverse() " George of the jungle"

Summary l l Binary trees seem simplified, but can actually do anything that an n-ary or even a linked list can do. Binary trees have useful applications (fast searching, equation representations). • • l A binary search tree places lesser items down the left branch and greater items down the right. As long as the tree remains balanced, O(log n) searching. Binary tree code tends to be small and recursive.