Binary Trees Binary tree structure Root Node stores

Binary Trees

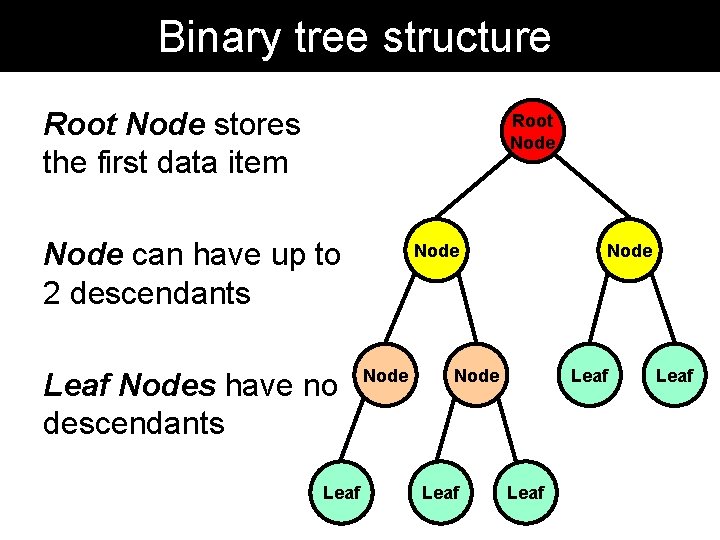
Binary tree structure Root Node stores the first data item Root Node can have up to 2 descendants Leaf Nodes have no descendants Leaf Node Leaf

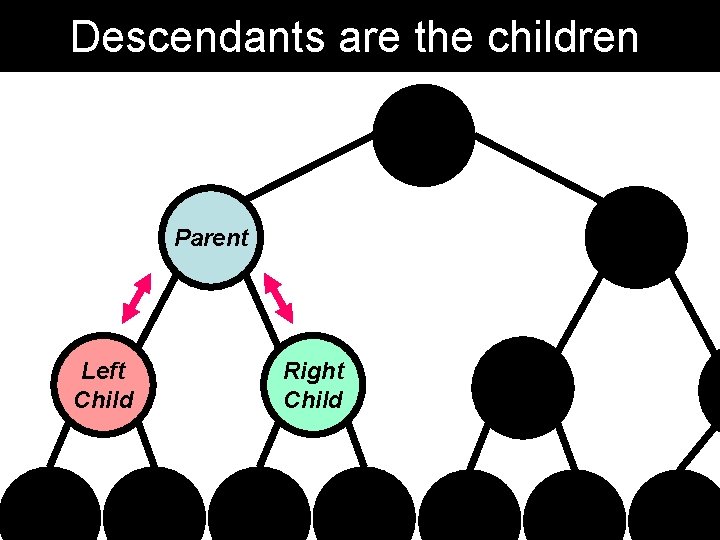
Descendants are the children Parent Left Child Right Child

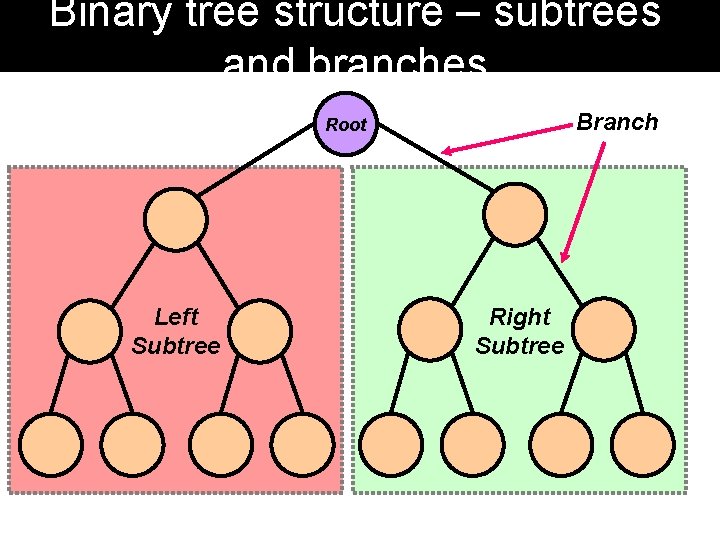
Binary tree structure – subtrees and branches Branch Root Left Subtree Right Subtree

Which way? Less than – Goes to the Left More than – Goes to the Right

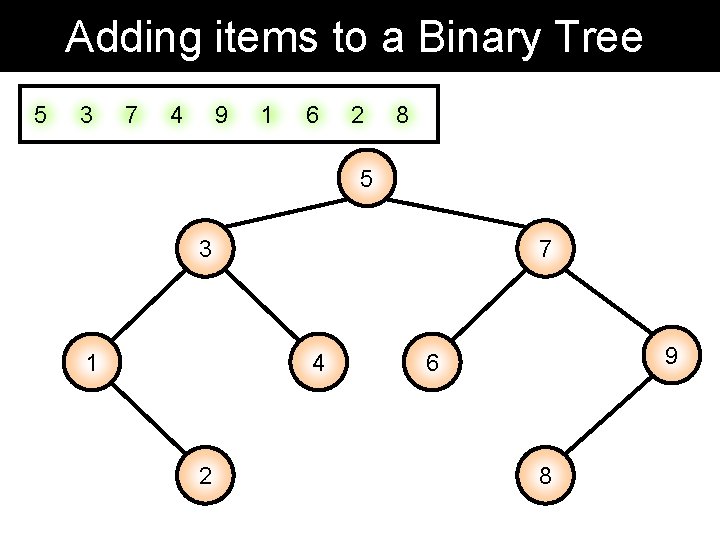
Adding items to a Binary Tree 5 3 7 4 9 1 6 2 8 5 3 1 7 4 2 9 6 8

Constructing a binary tree The following data items are to be stored in a binary tree: Daniel, Charles, Belinda, Cheryl, George and Fred. Daniel Charles Belinda Cheryl George Fred

Add a name to the binary tree To add the name Pete and Edward Daniel Charles Belinda George Cheryl Edward Fred Pete

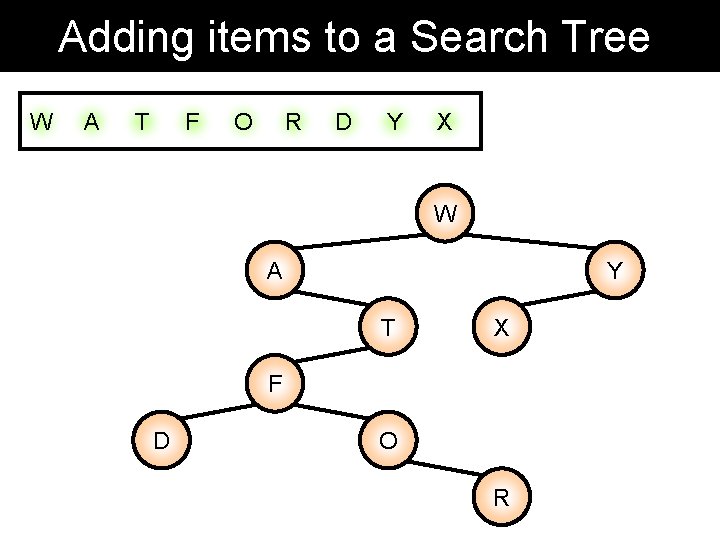
Adding items to a Search Tree W A T F O R D Y X W A Y T X F D O R

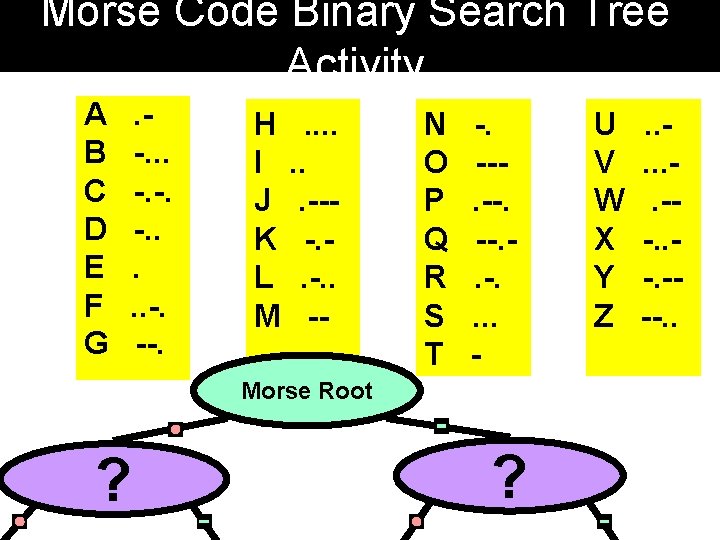
Morse Code Binary Search Tree Activity A B C D E F G . -. --. H. . I. . J. --K -. L. -. . M -- N O P Q R S T -. --. --. . . . - Morse Root ? ? U V W X Y Z . . . --. . -. ---. .

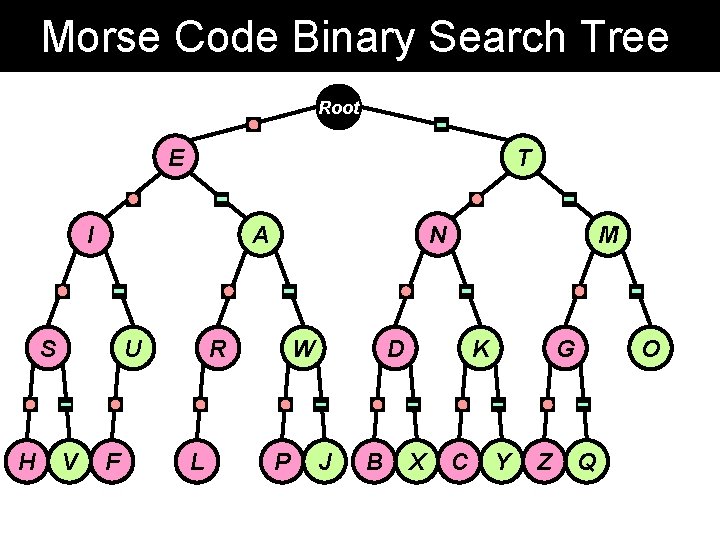
Morse Code Binary Search Tree Root E T I A S H U V F N R L W P M D J B K X C G Y Z O Q

Binary Tree Traversal Pre-Order In-Order Post-Order

What is traversal? Methods of looking at each node in a tree, in turn Recursive Pre-Order, In-Order, Post-Order Recursively Defined – Calls itself within itself Must have an End Condition

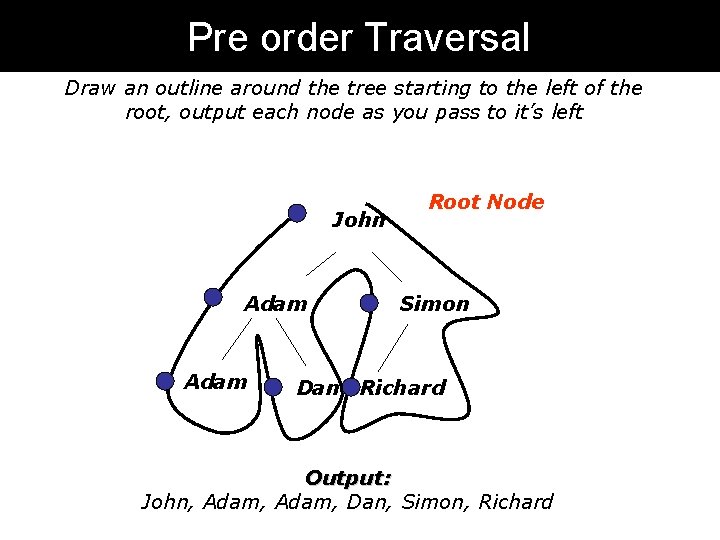
Pre order Traversal Draw an outline around the tree starting to the left of the root, output each node as you pass to it’s left John Adam Root Node Simon Dan Richard Output: John, Adam, Dan, Simon, Richard

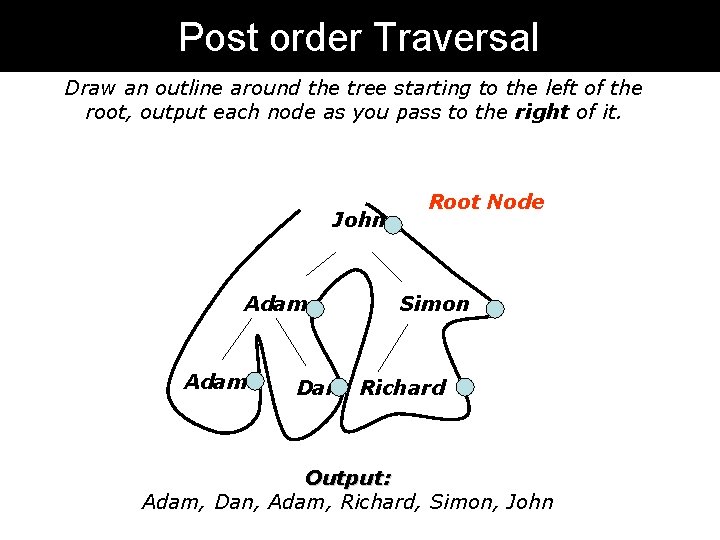
Post order Traversal Draw an outline around the tree starting to the left of the root, output each node as you pass to the right of it. John Adam Root Node Simon Dan Richard Output: Adam, Dan, Adam, Richard, Simon, John

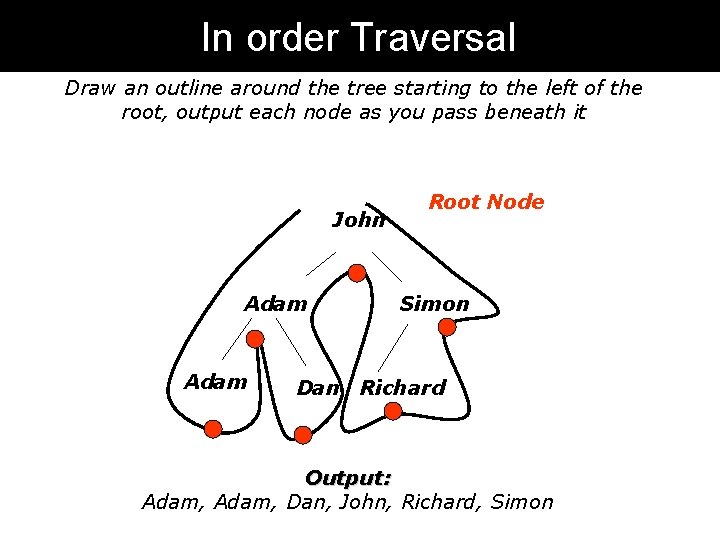
In order Traversal Draw an outline around the tree starting to the left of the root, output each node as you pass beneath it John Adam Root Node Simon Dan Richard Output: Adam, Dan, John, Richard, Simon

Golden Rules Pre – Left Post – Right In - Under

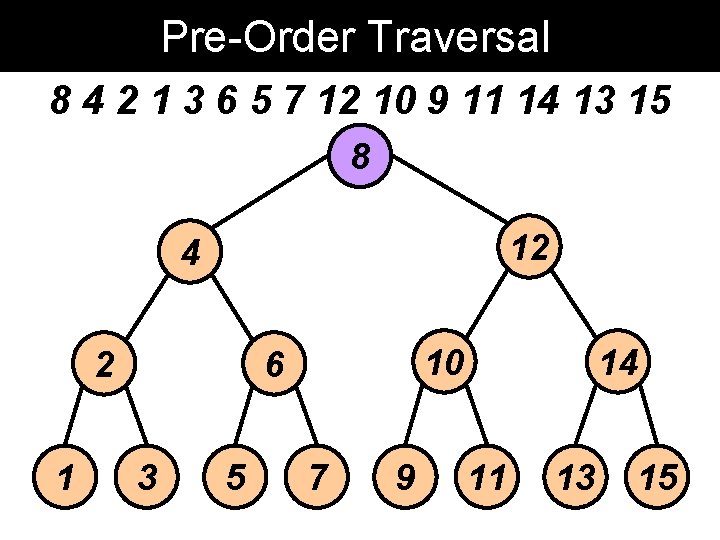
Pre-Order Traversal 8 4 2 1 3 6 5 7 12 10 9 11 14 13 15 8 12 4 2 1 10 6 3 5 7 9 14 11 13 15

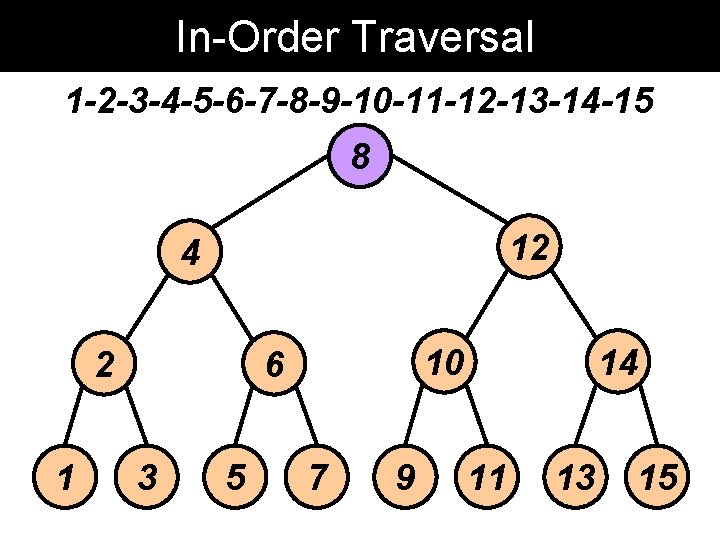
In-Order Traversal 1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 8 12 4 2 1 10 6 3 5 7 9 14 11 13 15

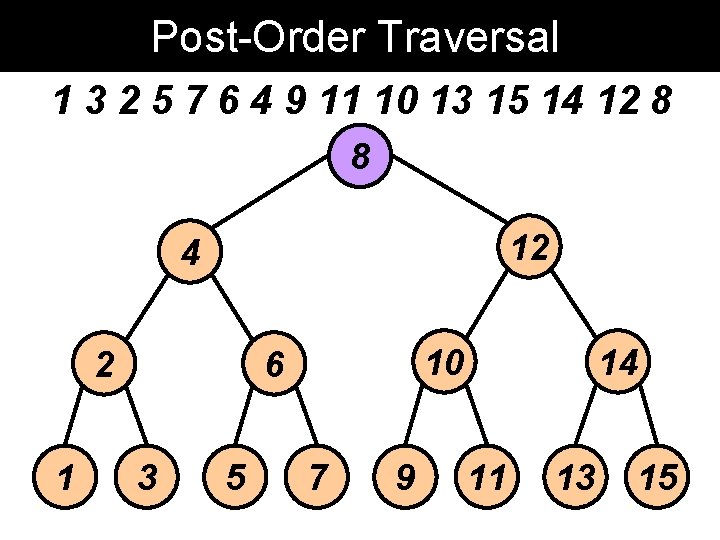
Post-Order Traversal 1 3 2 5 7 6 4 9 11 10 13 15 14 12 8 8 12 4 2 1 10 6 3 5 7 9 14 11 13 15

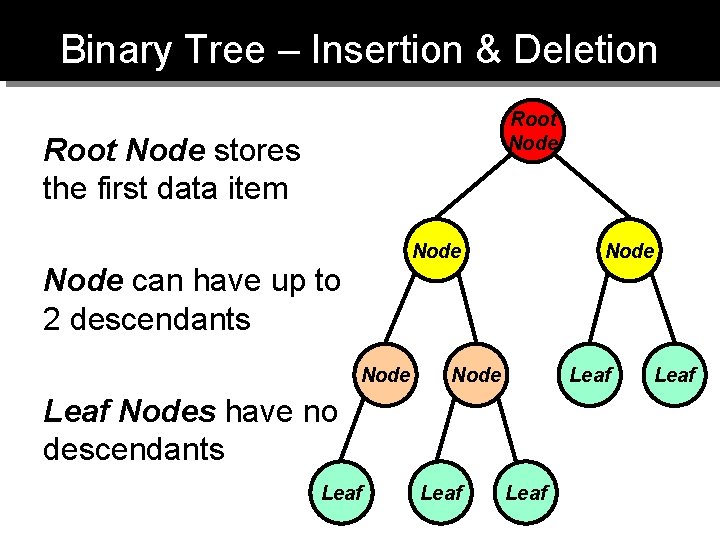
Binary Tree – Insertion & Deletion Root Node stores the first data item Node can have up to 2 descendants Node Leaf Nodes have no descendants Leaf

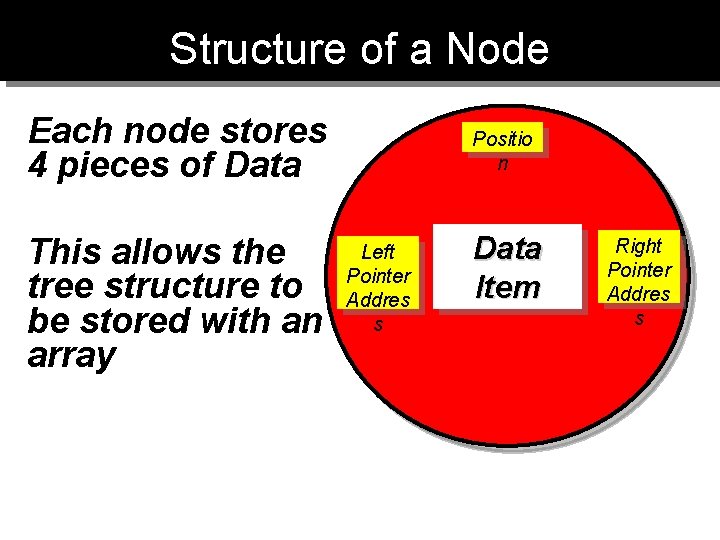
Structure of a Node Each node stores 4 pieces of Data This allows the tree structure to be stored with an array Positio n Left Pointer Addres s Data Item Right Pointer Addres s

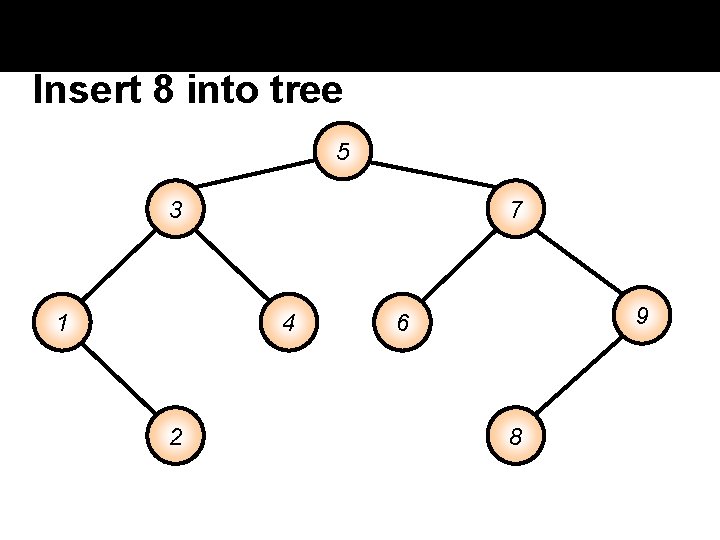
Insert 4 into tree Insert 8 into tree 5 3 1 7 4 2 9 6 8

Inserting a Node Pseudo Code Current. Node = Root Repeat If New. Node < Current. Node travel Left Else travel Right Current. Node = Node Reached Until Node = Null Create Node(New. Node)

Deleting a Node 2 Methods of removing a Node within a Tree Remove Node and all its sub Nodes Store Sub Nodes on a temp store (array) Reinsert each Node stored on temp store OR Set Data Item of deleted node to Null Leave node within structure