Binary Tree Sub Topik Penjelasan Tree Istilah pada

Binary Tree

Sub Topik • • • Penjelasan Tree Istilah pada tree Binary Tree Jenis Binary Tree ADT Binary tree

Tree (Pohon)

Real World leaves branches root

Computer Scientist’s View root leaves branches nodes

Definisi • Kumpulan node yang saling terhubung secara hirarki. • Hirarki = bertingkat. • Tiap node dapat berisi data dan link (penghubung) ke node lainnya • Tiap node memiliki satu induk, kecuali node root (akar) yang tidak memiliki induk. • Tiap node dapat memiliki anak dalam jumlah berapapun.

Linked list dan Tree • Linked list linear/serial data – Contoh : nama-nama mahasiswa dalam satu kelas. • Tree non linear/hierachically data – Contoh : tingkatan pegawai dalam perusahaan.

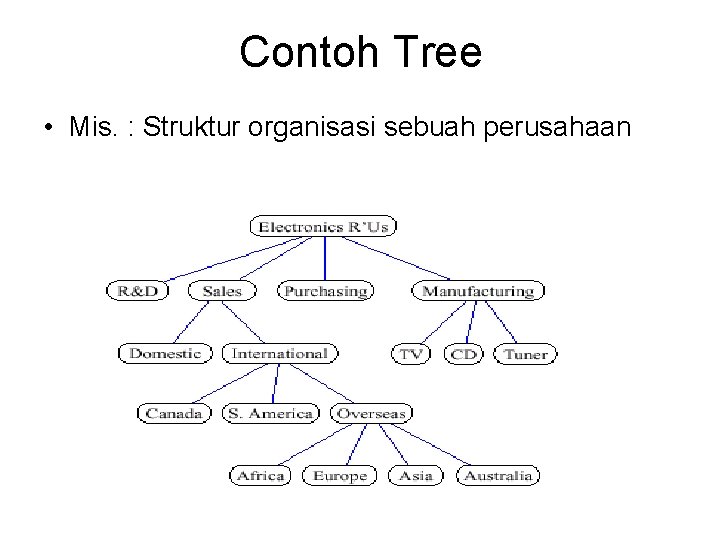
Contoh Tree • Mis. : Struktur organisasi sebuah perusahaan

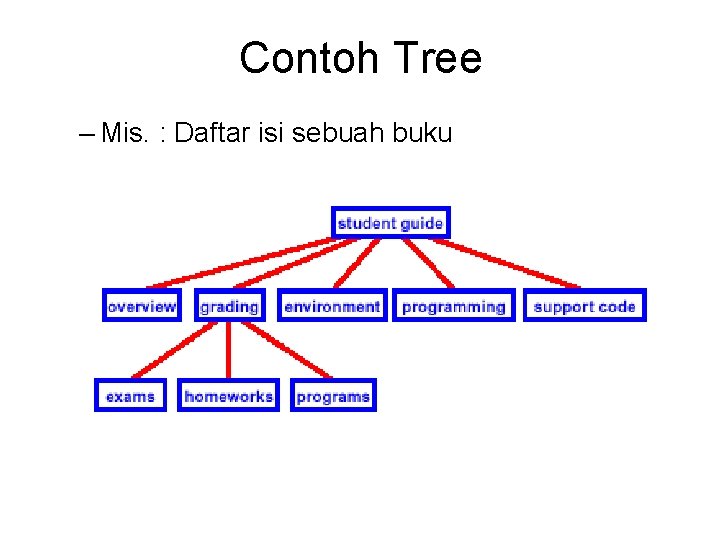
Contoh Tree – Mis. : Daftar isi sebuah buku

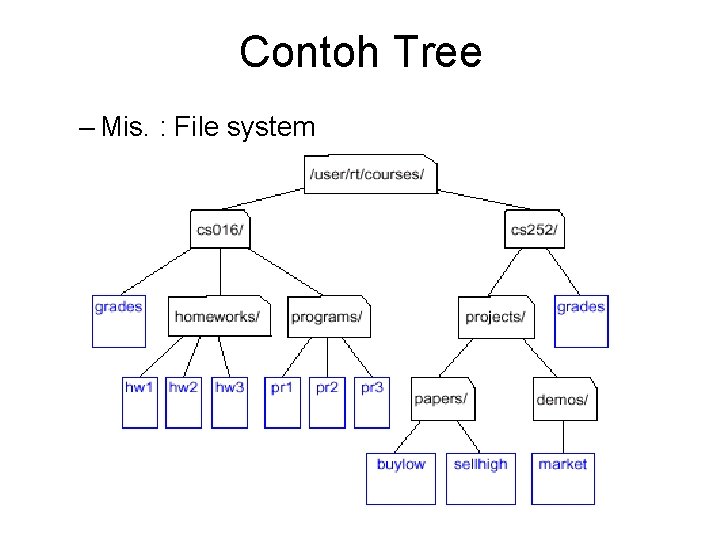
Contoh Tree – Mis. : File system

Tree (Pohon) • Root adalah node yang memiliki hirarki tertinggi. • Subtree (pohon anak) adalah beberapa node yang tersusun hirarki yang ada dibawah root.

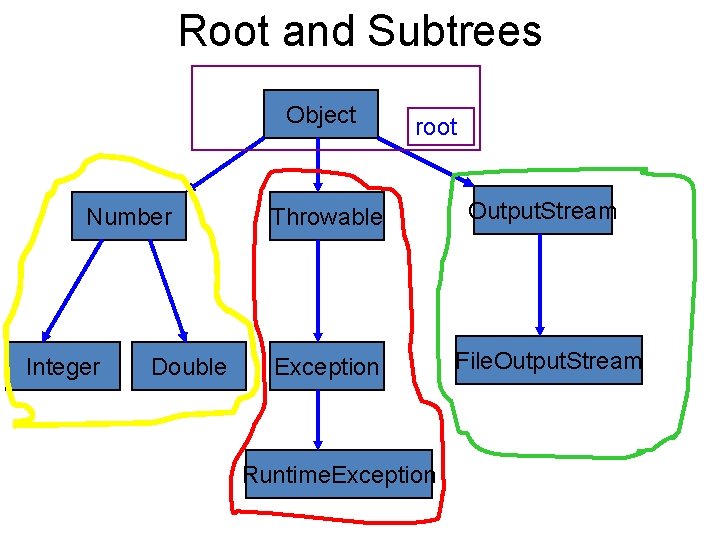
Root and Subtrees Object Number Integer Double root Throwable Output. Stream Exception File. Output. Stream Runtime. Exception

Tree (Pohon) • Level adalah posisi hirarki dari sebuah node. Untuk root bisa diberikan level 0 atau 1. • Leaf (Daun) adalah node yang tidak memiliki anak atau node yang berada pada hirarki paling bawah. • Height (tinggi)/depth adalah jumlah level dari sebuah tree.

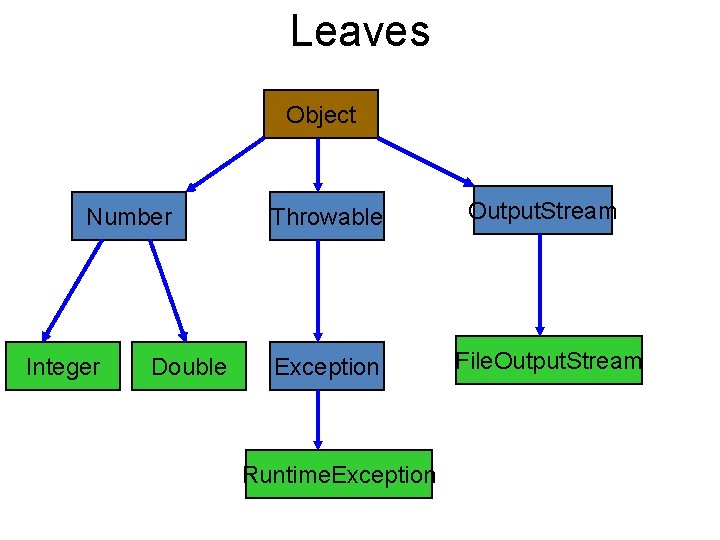
Leaves Object Number Integer Double Throwable Output. Stream Exception File. Output. Stream Runtime. Exception

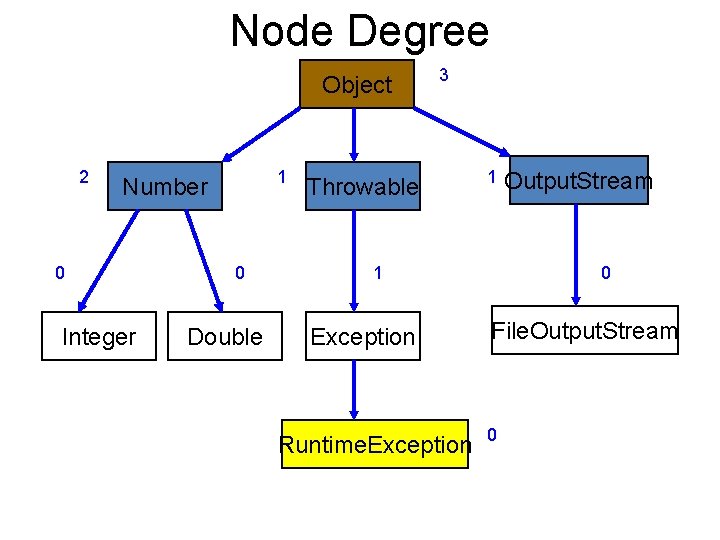
Node Degree Object 2 1 Number 0 Integer 0 Double 3 Throwable 1 1 Exception Runtime. Exception Output. Stream 0 File. Output. Stream 0

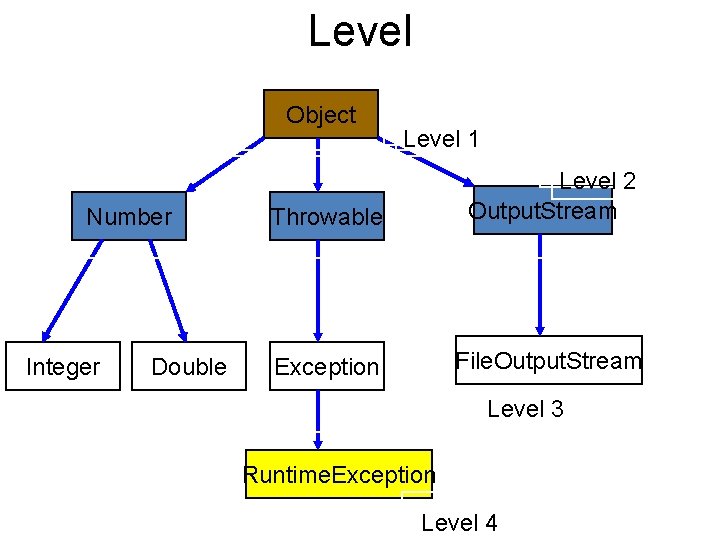
Level Object Number Integer Double Throwable Exception Level 11 Level 2 Output. Stream File. Output. Stream Level 33 Runtime. Exception Level 44

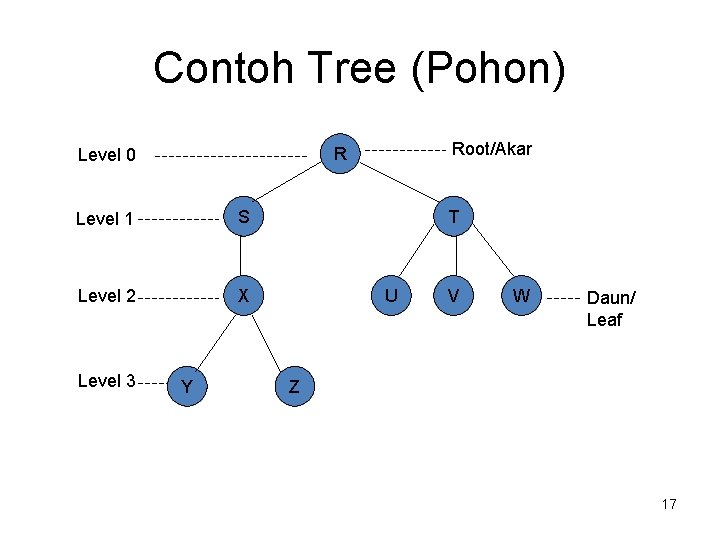
Contoh Tree (Pohon) Level 1 S Level 2 X Level 3 Root/Akar R Level 0 Y T U V W Daun/ Leaf Z 17

Istilah Tree (Pohon)

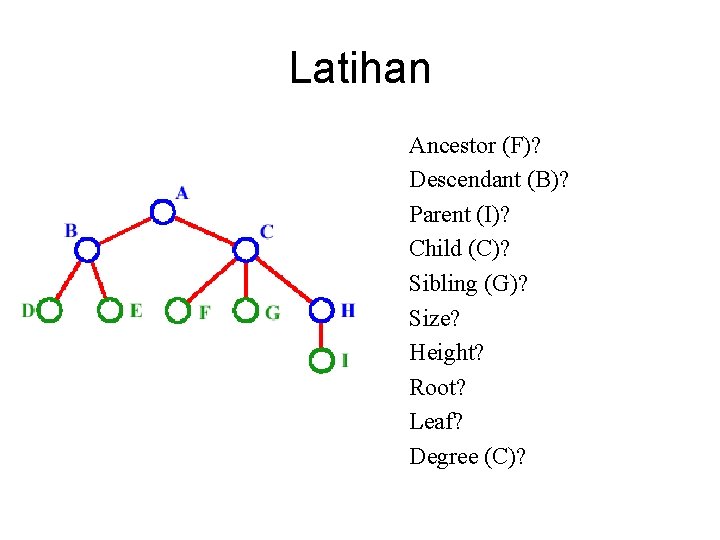
Latihan Ancestor (F)? Descendant (B)? Parent (I)? Child (C)? Sibling (G)? Size? Height? Root? Leaf? Degree (C)?

Tree (Pohon) • Dimana, Ancestor (F) = C, A Descendant (B) = D, E Parent (I) = H Child (A) = B, C Sibling (F) = G, H Size = 9 Height = 3/4 Root = A Leaf = D, E, F, G, I Degree (C) = 3

Binary Tree

Gambar Binary Trees

Binary Tree • Tiap node pada binary tree hanya boleh memiliki paling banyak dua child. • Sehingga hanya ada dua subtree pada binary tree yang disebut sebagai left dan right subtrees.

Tree dan Binary Tree • Pada binary tree nilai degree tidak lebih dari 2, sedangkan pada tree tidak terbatas. • Sub tree pada binary harus terurut (ordered), sedangkan pada tree tidak (un-ordered).

Jenis Binary Tree • Berdasarkan subtree binary tree dibedakan menjadi 4 jenis: – Full Binary Tree – Complete Binary Tree – Incomplete Binary Tree (Unbalanced Tree) – Skewed Binary Tree

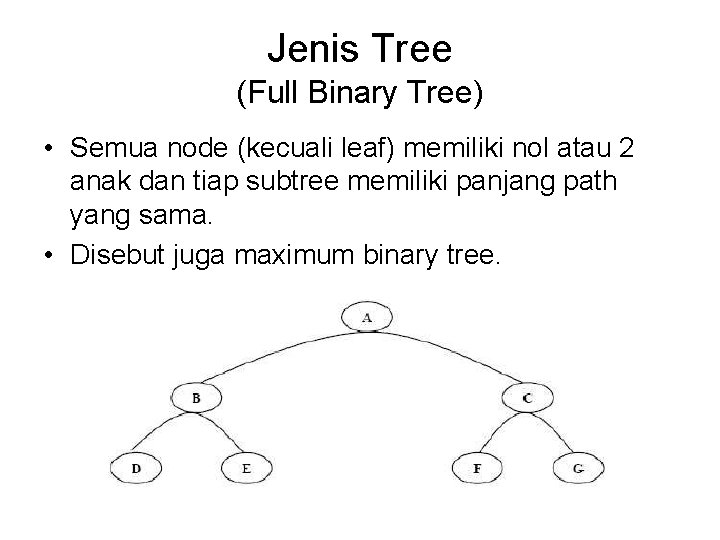
Jenis Tree (Full Binary Tree) • Semua node (kecuali leaf) memiliki nol atau 2 anak dan tiap subtree memiliki panjang path yang sama. • Disebut juga maximum binary tree.

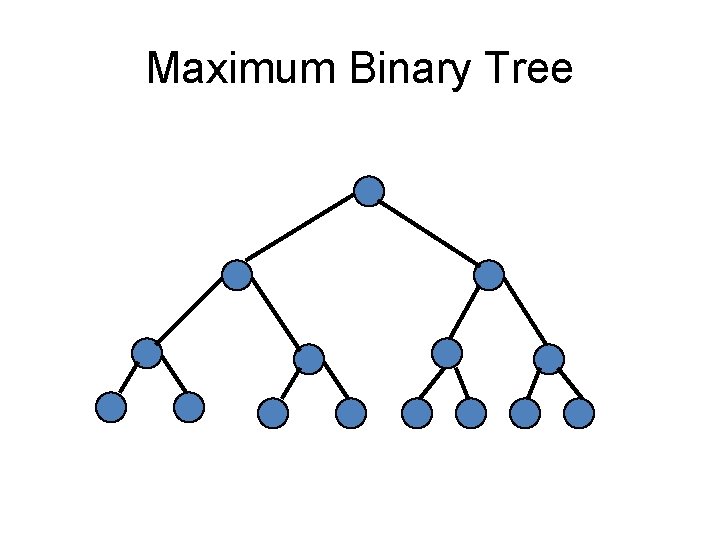
Maximum Binary Tree

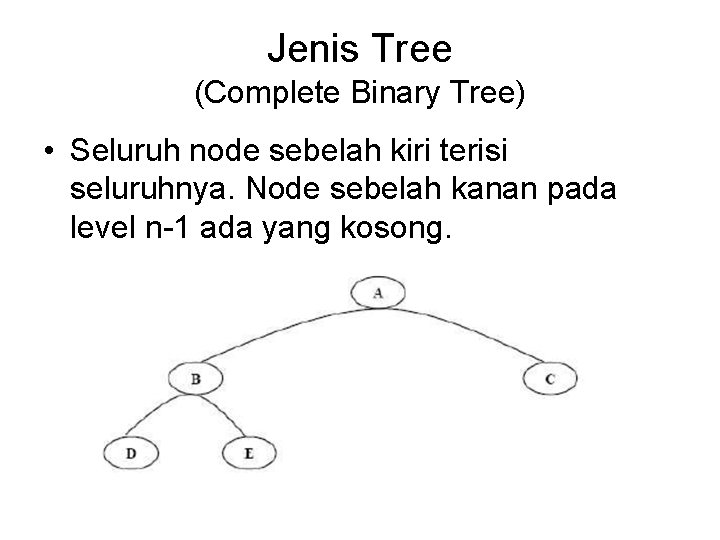
Jenis Tree (Complete Binary Tree) • Seluruh node sebelah kiri terisi seluruhnya. Node sebelah kanan pada level n-1 ada yang kosong.

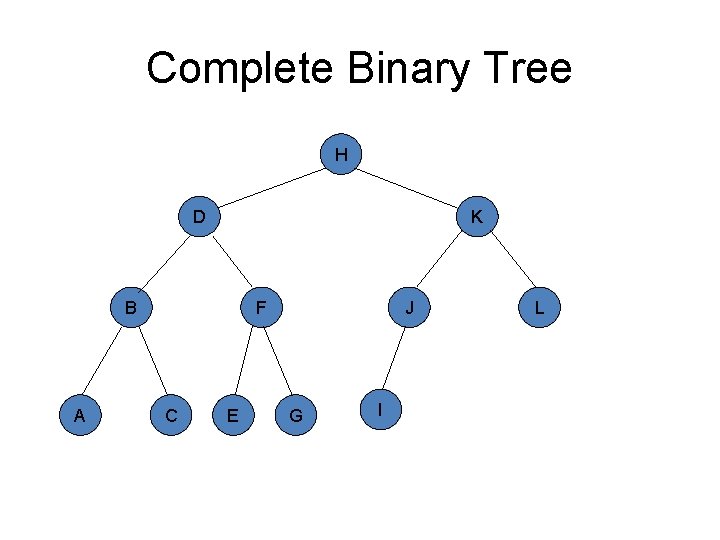
Complete Binary Tree H D K B A F C E J G I L

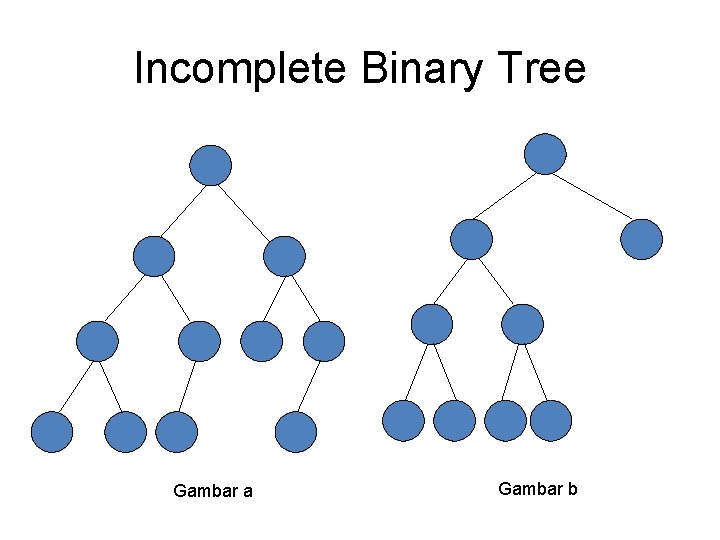
Incomplete Binary Tree Gambar a Gambar b

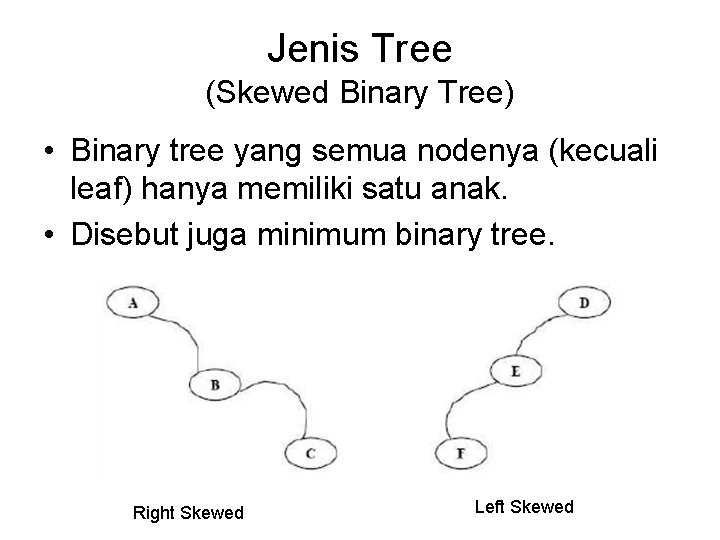
Jenis Tree (Skewed Binary Tree) • Binary tree yang semua nodenya (kecuali leaf) hanya memiliki satu anak. • Disebut juga minimum binary tree. Right Skewed Left Skewed

Binary Tree Representation

Representation • Array representation • Linked list representation

ADT Binary. Tree public interface Binary. Tree { public boolean is. Empty(); public Object root(); public void make. Tree(Object root, Object left, Object right); public Binary. Tree remove. Left. Subtree(); public Binary. Tree remove. Right. Subtree(); public void pre. Order(Method visit); public void in. Order(Method visit); public void post. Order(Method visit); public void level. Order(Method visit); }

Array Representation

Akses Elemen • Posisi node dapat ditentukan berdasarkan rumus berikut : – Anak kiri dari node i berada pada indeks : 2*i+1 – Anak kanan dari node i berada pada indeks : 2*i+2 Struktur Data - Tree 36

Penambahan array size • • 1 node (root) = 20 Root + node pada level 1 = 20 +21 Root + node pada level 1 & 2 = 20 +21+22 Root + node pada level 1, 2, 3 = 20 +21 +22 +23 • Root + node pada level 1, 2, . . n=20+21+22+. . . +2 n

Array Representation a 1 22 b 44 88 d h tree[] 99 10 10 i j 33 c 55 e 66 77 g f a b c d e f g h i j 0 0 5 5 10 10

Right-Skewed Binary Tree 11 a 33 b 77 c d tree[] a 0 0 15 15 b - - - c - - - - d 5 10 15

Linked List Representation

Class Binary. Tree. Node class Binary. Tree. Node { Object element; Binary. Tree. Node left. Child; // left subtree Binary. Tree. Node right. Child; // right subtree // constructors and any other methods come here }

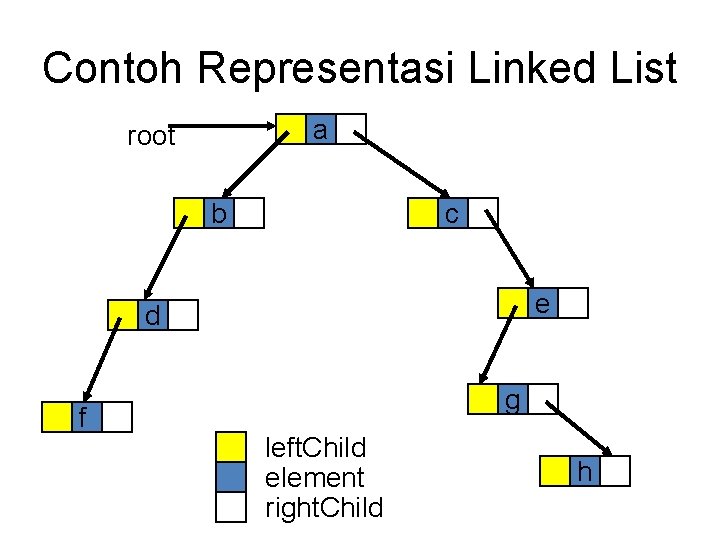
Contoh Representasi Linked List root a b c e d f g left. Child element right. Child h

Binary Tree Traversal

Definisi • Penelusuran seluruh node pada binary tree. • Metode : – Preorder – Inorder – Postorder – Level order

Preorder Traversal public static void pre. Order(Binary. Tree. Node t) { if (t != null) { visit(t); pre. Order(t. left. Child); pre. Order(t. right. Child); } }

Pre. Order Traversal • Preorder traversal 1. Cetak data pada root 2. Secara rekursif mencetak seluruh data pada subpohon kiri 3. Secara rekursif mencetak seluruh data pada subpohon kanan

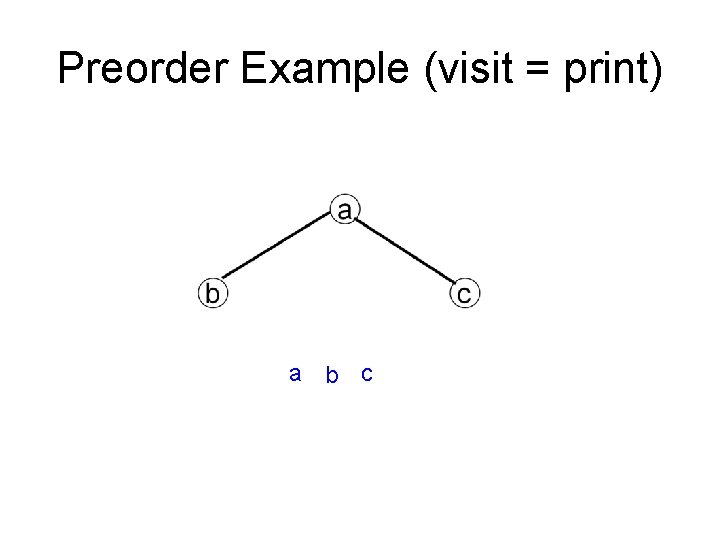
Preorder Example (visit = print) a b c

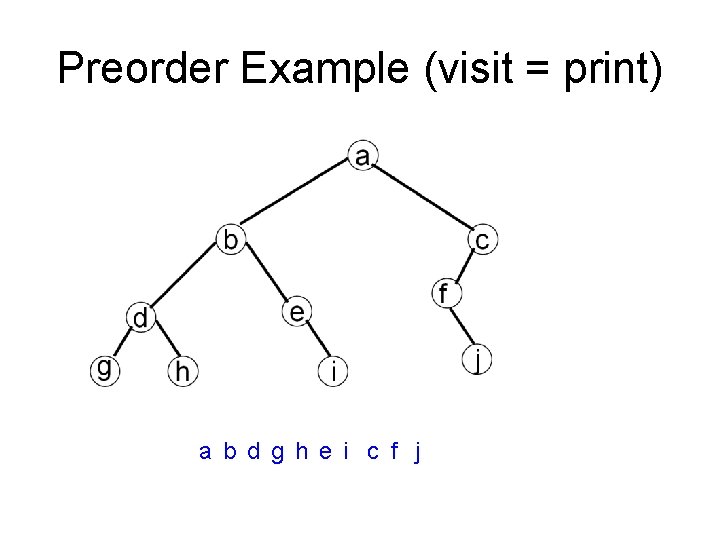
Preorder Example (visit = print) a b d g h e i c f j

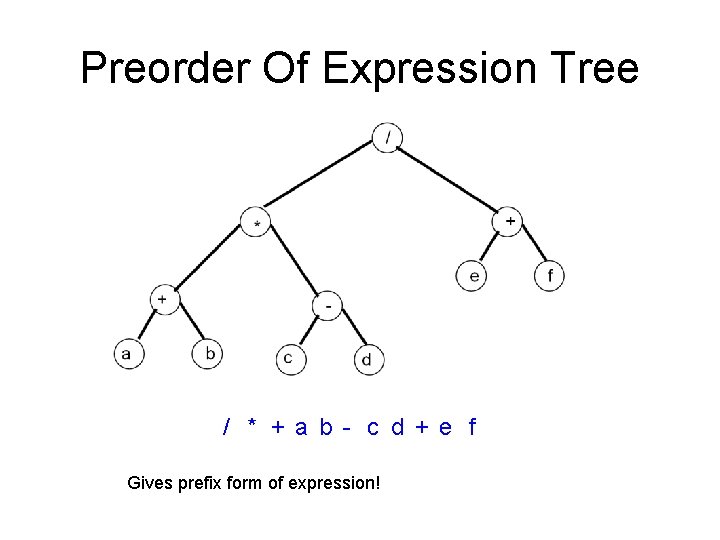
Preorder Of Expression Tree / * + a b - c d + e f Gives prefix form of expression!

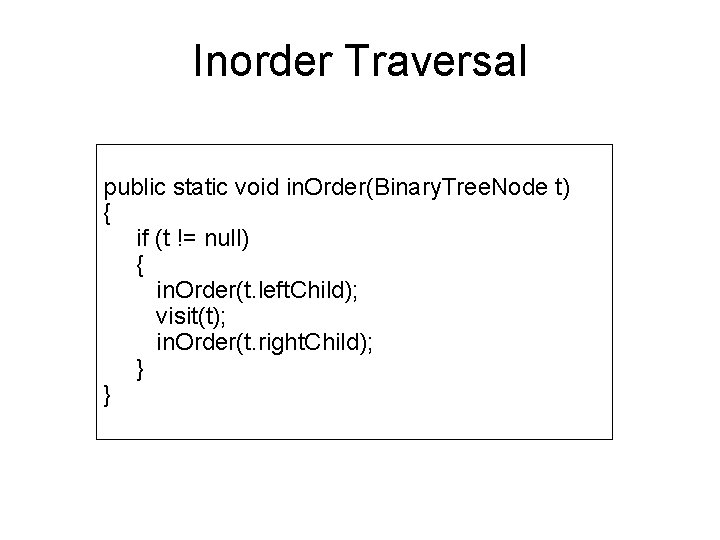
Inorder Traversal public static void in. Order(Binary. Tree. Node t) { if (t != null) { in. Order(t. left. Child); visit(t); in. Order(t. right. Child); } }

In. Order Traversal • Inorder traversal 1. Secara rekursif mencetak seluruh data pada subpohon kiri 2. Cetak data pada root 3. Secara rekursif mencetak seluruh data pada subpohon kanan

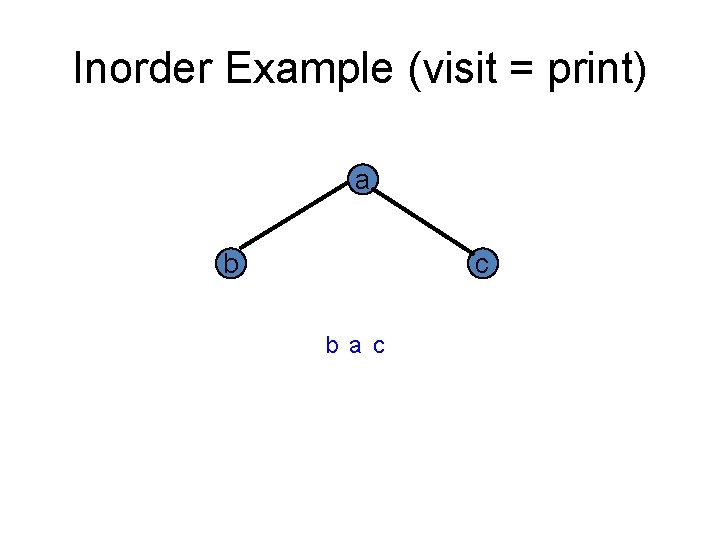
Inorder Example (visit = print) a b c b a c

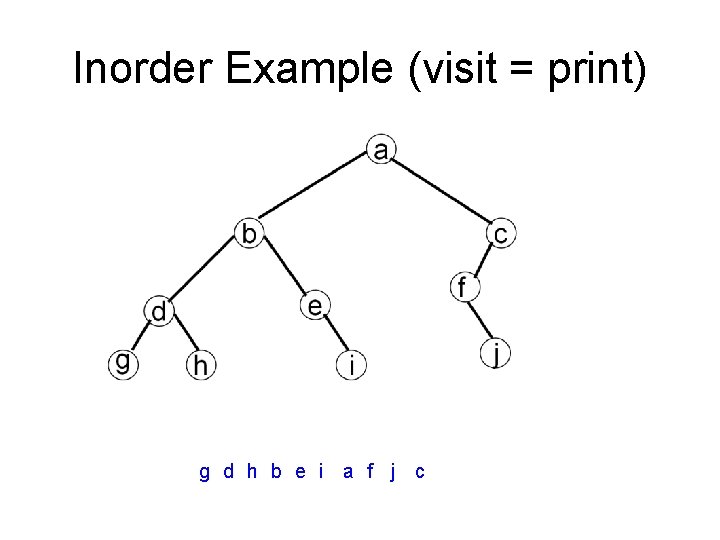
Inorder Example (visit = print) g d h b e i a f j c

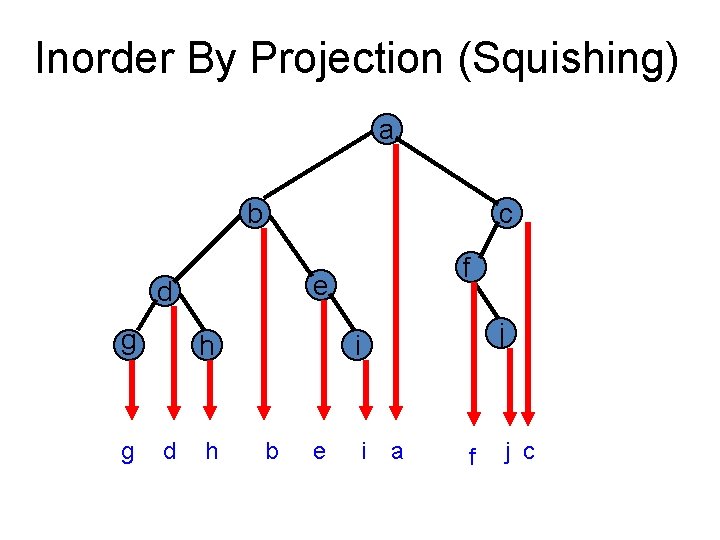
Inorder By Projection (Squishing) a b c e d g g h d f h j i b e i a f j c

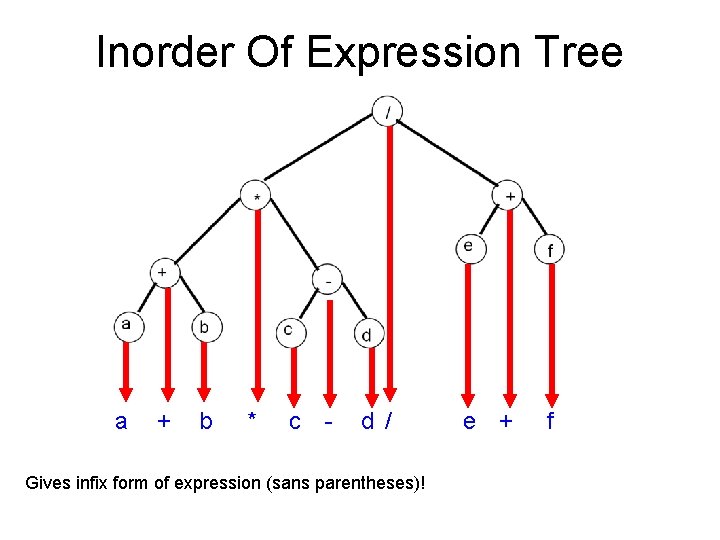
Inorder Of Expression Tree a + b * c - d / Gives infix form of expression (sans parentheses)! e + f

Postorder Traversal public static void post. Order(Binary. Tree. Node t) { if (t != null) { post. Order(t. left. Child); post. Order(t. right. Child); visit(t); } }

Postorder Traversal • Postorder traversal 1. Secara rekursif mencetak seluruh data pada subpohon kiri 2. Secara rekursif mencetak seluruh data pada subpohon kanan 3. Cetak data pada root

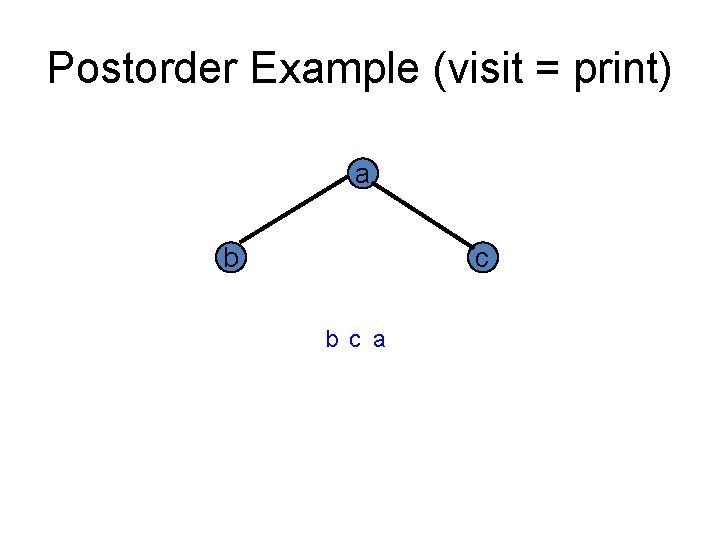
Postorder Example (visit = print) a b c a

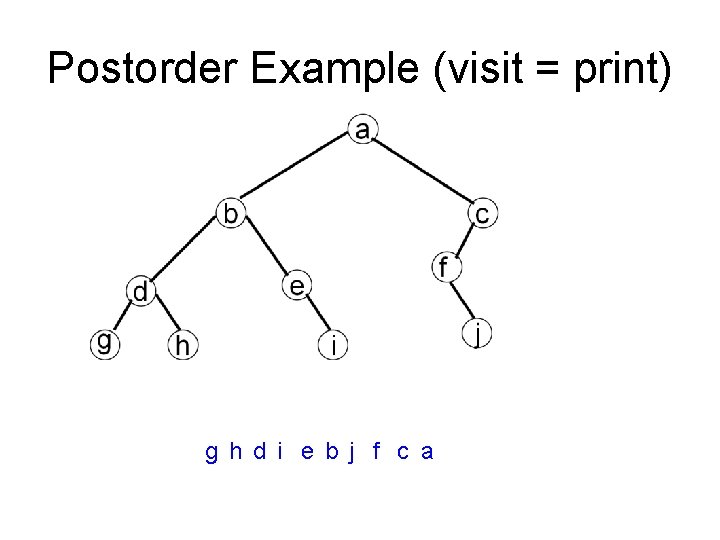
Postorder Example (visit = print) g h d i e b j f c a

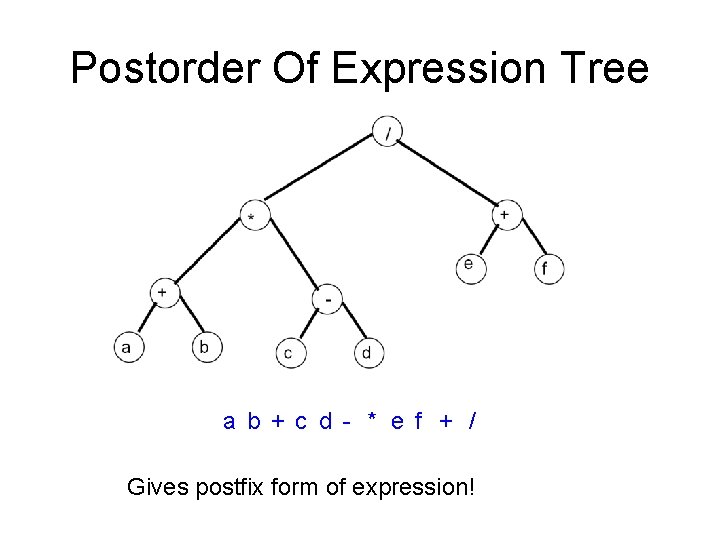
Postorder Of Expression Tree a b + c d - * e f + / Gives postfix form of expression!

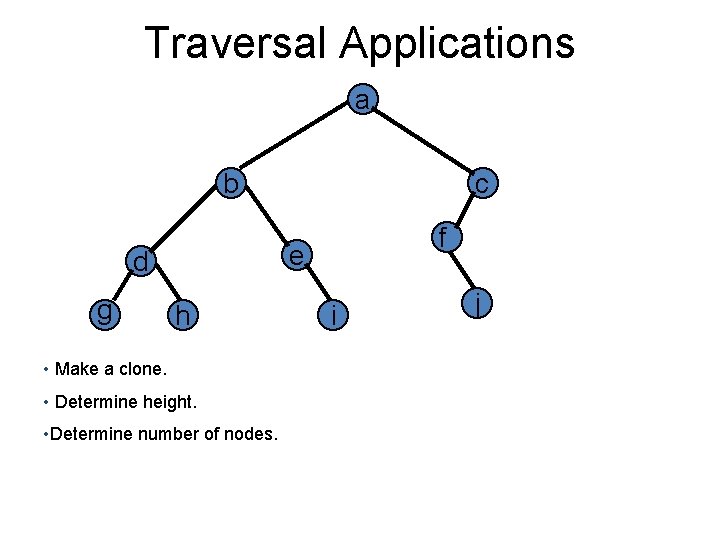
Traversal Applications a b f e d g c h • Make a clone. • Determine height. • Determine number of nodes. i j

Level Order Let t be the tree root. while (t != null) { visit t and put its children on a FIFO queue; remove a node from the FIFO queue and call it t; // remove returns null when queue is empty }

Latihan • Telusuri pohon biner berikut dengan menggunakan metode pre, in, post, dan level traversal.

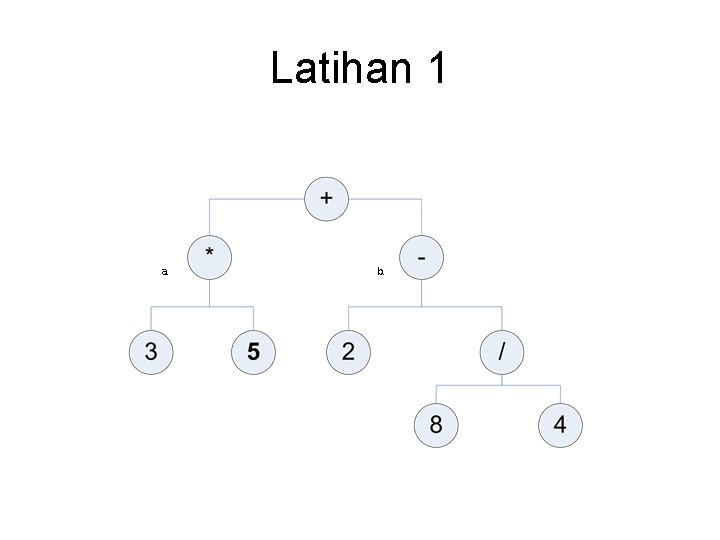
Latihan 1 a. b.

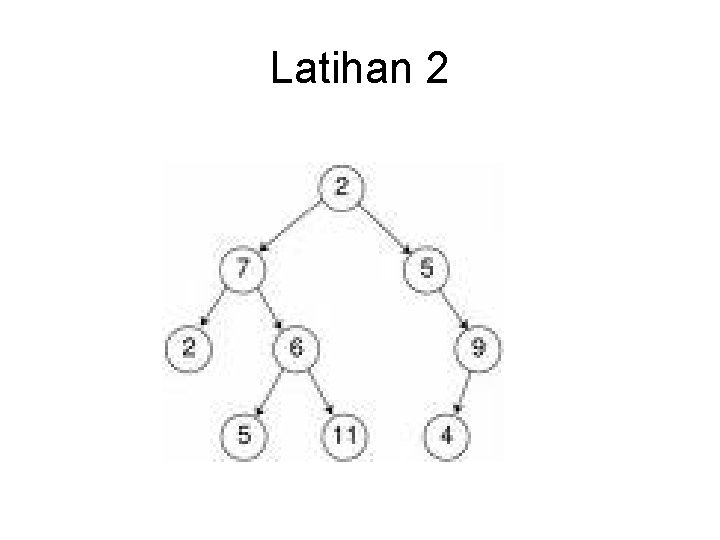
Latihan 2

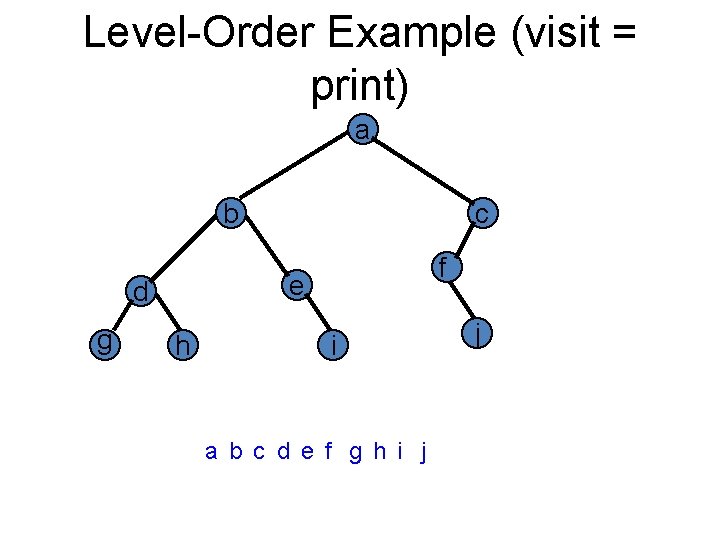
Level-Order Example (visit = print) a b f e d g c h i a b c d e f g h i j j

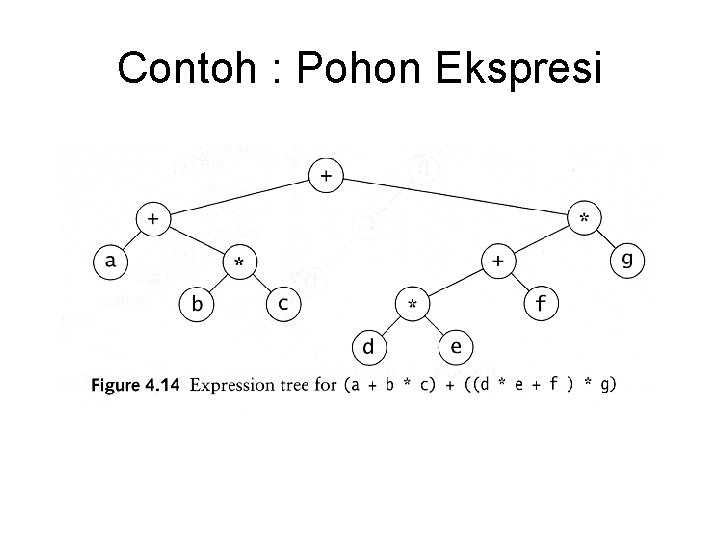
Contoh : Pohon Ekspresi

Pre. Order, Post. Order, In. Order • Pre-order : – Node, left, right – Ekspresi Prefix : ++a*bc*+*defg • Post-order : – Node, left, right – Ekspresi Postfix : abc*+de*f+g*+ • In-order : – Node, left, right – Ekspresi Infix : a+b*c+d*e+f*g

Pustaka • Sartaj Sahni , “Data Structures & Algorithms”, Presentation L 20 -24. • Mitchell Waite, “Data Structures & Algorithms in Java”, SAMS, 2001