Binary Search Trees Why this is a useful

Binary Search Trees • Why this is a useful data structure. • Terminology • Implementation Considerations

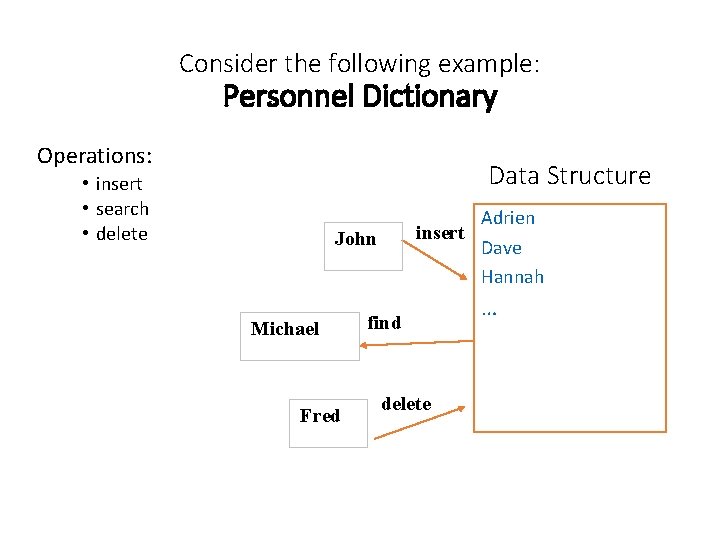
Consider the following example: Personnel Dictionary Operations: Data Structure • insert • search • delete insert John Michael Fred find delete Adrien Dave Hannah …

Personnel Dictionary Data Structure Requirements • Fast insertion runtime • Fast searching runtime • Fast deletion runtime

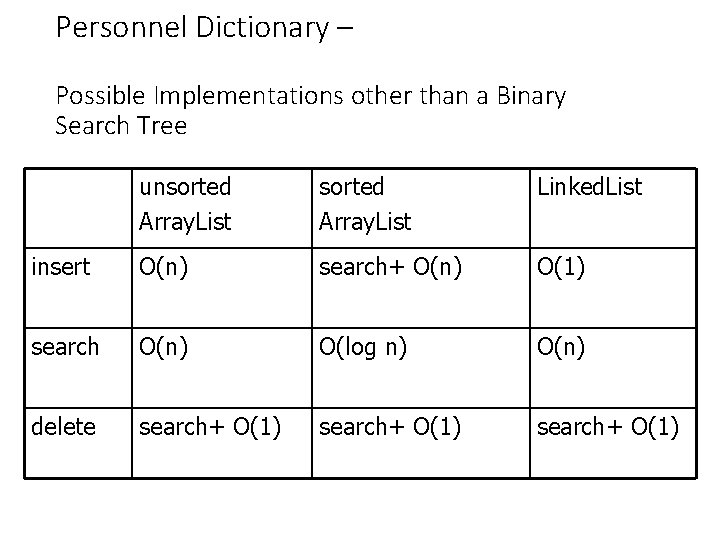
Personnel Dictionary – Possible Implementations other than a Binary Search Tree unsorted Array. List Linked. List insert O(n) search+ O(n) O(1) search O(n) O(log n) O(n) delete search+ O(1)

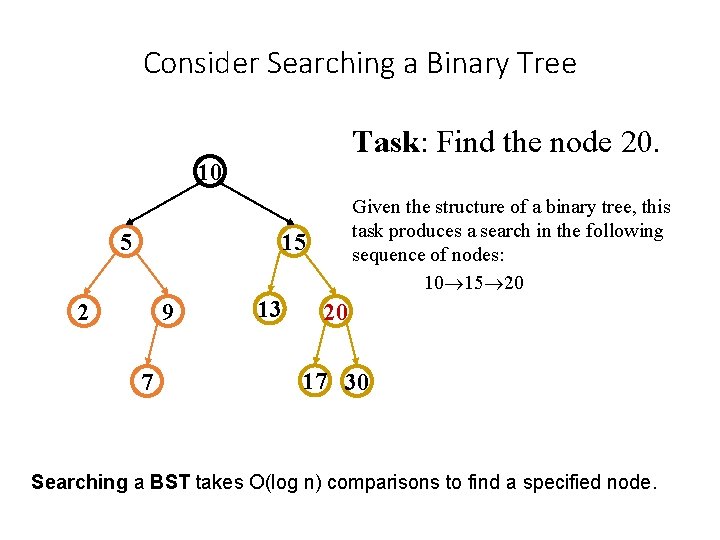
Consider Searching a Binary Tree Task: Find the node 20. 10 5 Given the structure of a binary tree, this task produces a search in the following sequence of nodes: 10 15 2 9 7 13 20 17 30 Searching a BST takes O(log n) comparisons to find a specified node.

Compare searches within data structures: BST unsorted Array. List Linked. List O(log n) O(n) Given the structure of a BST: Search: O(log n). Insertion: O(log n). Deletion: O(log n).

Why are Binary Trees useful data structures? • The time it takes to search a linked lists is often prohibitive. • The time it takes to delete an item in an array is prohibitive. • Sorting a large array is prohibitive. • A tree structure is efficient for search, insertion, and deletion. This is the only data structure for which the running time of most operations (search, insert, delete) is O(log N)?

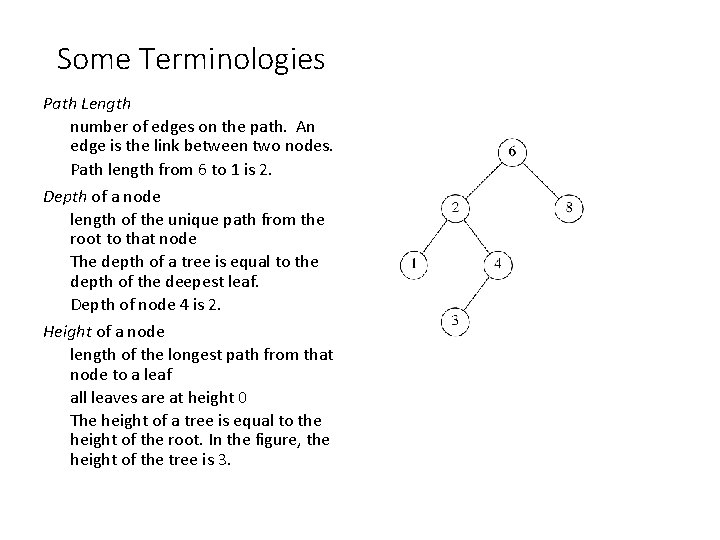
Some Terminologies Path Length number of edges on the path. An edge is the link between two nodes. Path length from 6 to 1 is 2. Depth of a node length of the unique path from the root to that node The depth of a tree is equal to the depth of the deepest leaf. Depth of node 4 is 2. Height of a node length of the longest path from that node to a leaf all leaves are at height 0 The height of a tree is equal to the height of the root. In the figure, the height of the tree is 3.

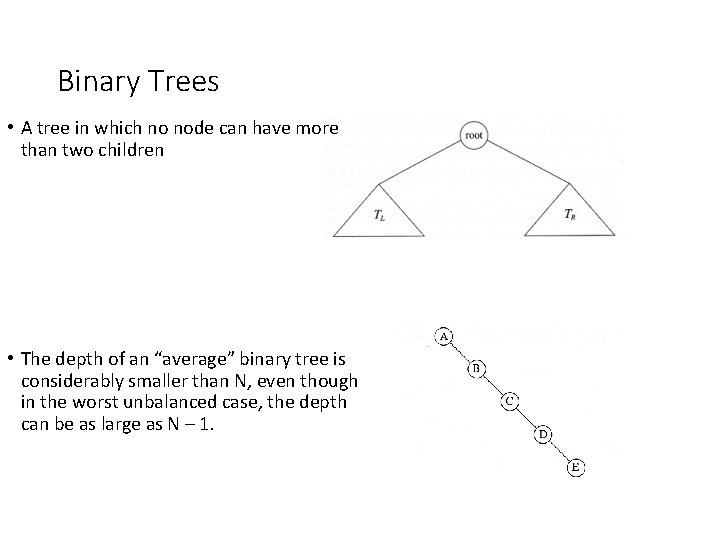
Binary Trees • A tree in which no node can have more than two children • The depth of an “average” binary tree is considerably smaller than N, even though in the worst unbalanced case, the depth can be as large as N – 1.

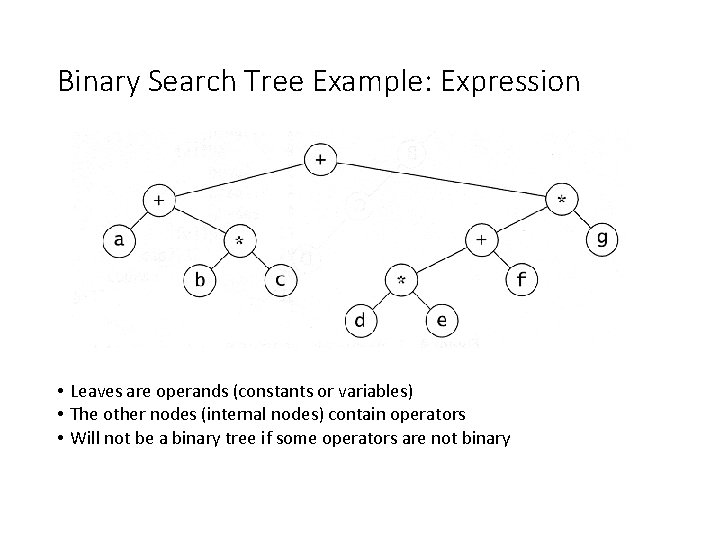
Binary Search Tree Example: Expression • Leaves are operands (constants or variables) • The other nodes (internal nodes) contain operators • Will not be a binary tree if some operators are not binary

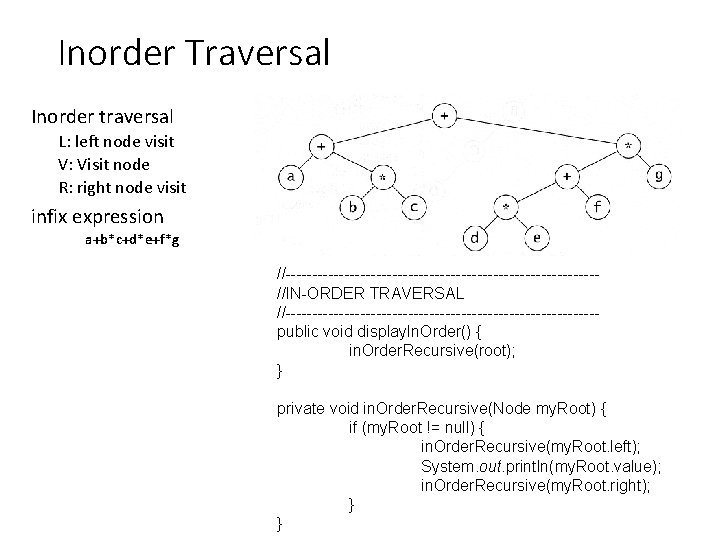
Inorder Traversal Inorder traversal L: left node visit V: Visit node R: right node visit infix expression a+b*c+d*e+f*g //-----------------------------//IN-ORDER TRAVERSAL //-----------------------------public void display. In. Order() { in. Order. Recursive(root); } private void in. Order. Recursive(Node my. Root) { if (my. Root != null) { in. Order. Recursive(my. Root. left); System. out. println(my. Root. value); in. Order. Recursive(my. Root. right); } }

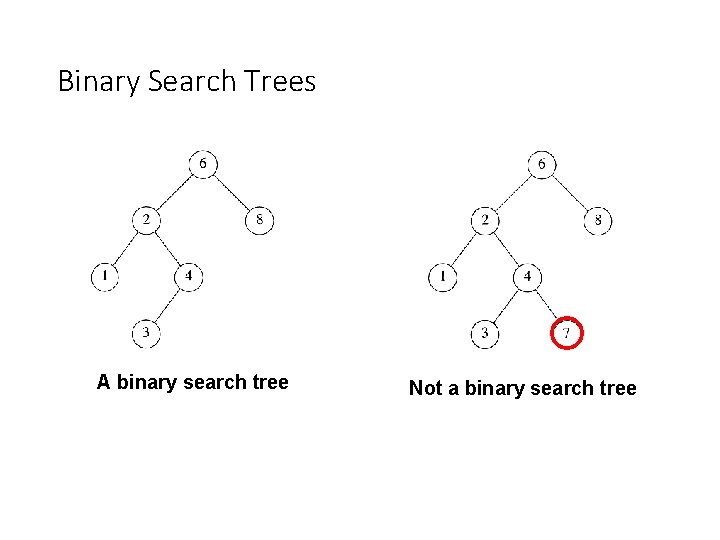
Binary Search Trees A binary search tree Not a binary search tree

Binary search trees Two binary search trees representing the same set. The first tree is balanced. • Average depth of a node is O(log N); • maximum depth of a node is O(N)

Implementation for a BST Class: l add. Node() l search. Node() l display. Tree() l delete. Node()

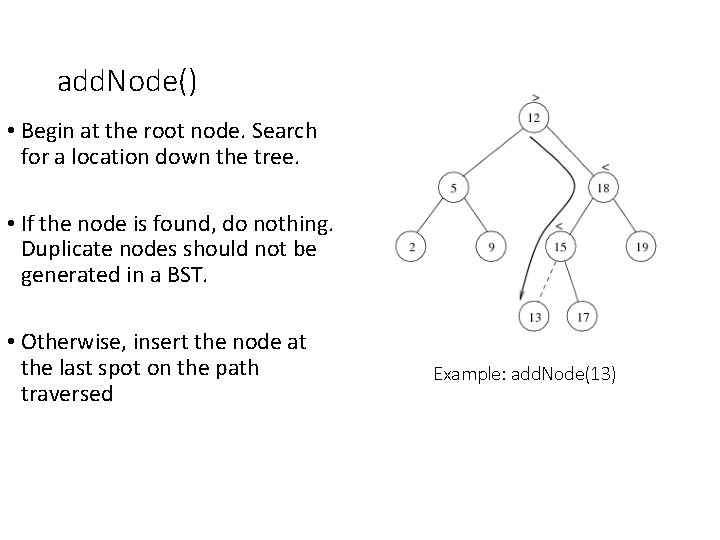
add. Node() • Begin at the root node. Search for a location down the tree. • If the node is found, do nothing. Duplicate nodes should not be generated in a BST. • Otherwise, insert the node at the last spot on the path traversed Example: add. Node(13)

search. Node() • Begin search at the root. If we find the node we are searching for, then we are done. • If we are searching for a node with a value less than the current node, then we should search in the left subtree. • If we are searching for a node with a value greater than the current node, then we should search in the right subtree.

delete. Node() Important: • When we delete a node, we need to consider how to re-assign the children of the deleted node.

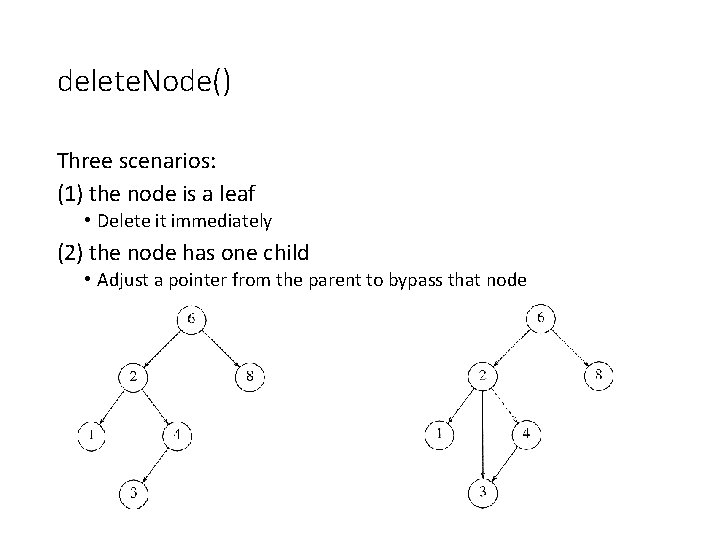
delete. Node() Three scenarios: (1) the node is a leaf • Delete it immediately (2) the node has one child • Adjust a pointer from the parent to bypass that node

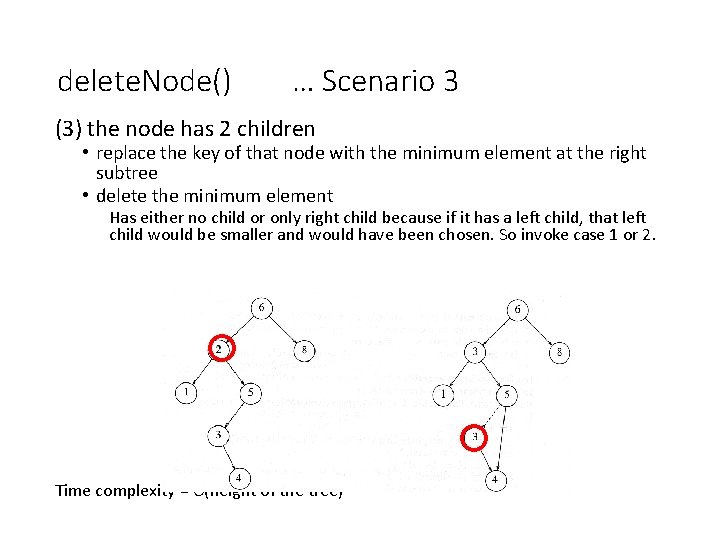
delete. Node() … Scenario 3 (3) the node has 2 children • replace the key of that node with the minimum element at the right subtree • delete the minimum element Has either no child or only right child because if it has a left child, that left child would be smaller and would have been chosen. So invoke case 1 or 2. Time complexity = O(height of the tree)

Try: find. Min() and find. Max() • Return the node containing the smallest element in the tree • Start at the root and go left as long as there is a left child. The stopping point is the smallest element • Similarly for find. Max • Time complexity = O(height of the tree)