Binary Search Trees Tree traversals BST properties Search

Binary Search Trees Tree traversals BST properties Search Insertion October 30, 2017 Hassan Khosravi / Geoffrey Tien 1

Binary tree traversal • A traversal algorithm for a binary tree visits each node in the tree – Typically, it will do something while visiting each node! • Traversal algorithms are naturally recursive • There are three traversal methods – in. Order – pre. Order – post. Order October 30, 2017 Hassan Khosravi / Geoffrey Tien 2

in. Order traversal algorithm void in. Order(BNode* nd) { if (nd != NULL) { in. Order(nd->left); visit(nd); in. Order(nd->right); } } typedef struct BNode { int data; struct BNode* left; struct BNode* right; } BNode; The visit function would do whatever the purpose of the traversal is (e. g. print the data value of the node). October 30, 2017 Hassan Khosravi / Geoffrey Tien 3

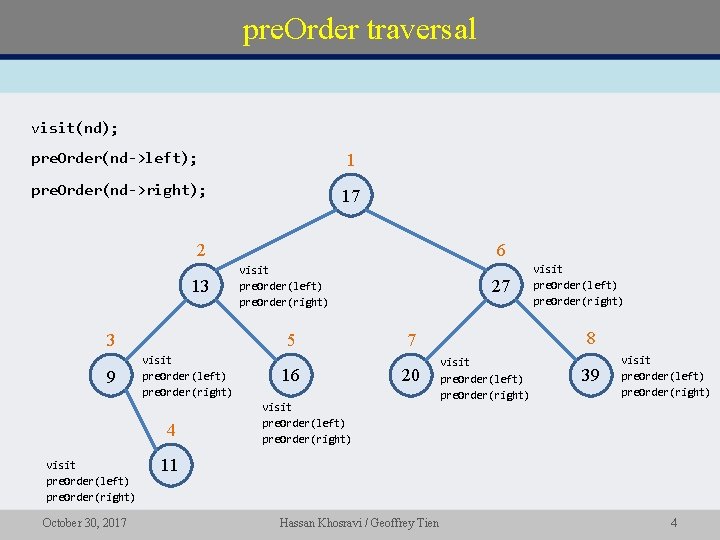
pre. Order traversal visit(nd); pre. Order(nd->left); 1 pre. Order(nd->right); 17 2 13 visit pre. Order(left) pre. Order(right) 4 visit pre. Order(left) pre. Order(right) October 30, 2017 visit pre. Order(left) pre. Order(right) 5 3 9 6 16 27 8 7 20 visit pre. Order(left) pre. Order(right) 39 visit pre. Order(left) pre. Order(right) 11 Hassan Khosravi / Geoffrey Tien 4

post. Order traversal post. Order(nd->left); post. Order(nd->right); 8 visit(nd); 17 4 13 7 post. Order(left) post. Order(right) visit 3 2 9 post. Order(left) post. Order(right) visit 1 post. Order(left) post. Order(right) visit October 30, 2017 16 27 post. Order(left) post. Order(right) visit 6 5 20 post. Order(left) post. Order(right) visit 39 post. Order(left) post. Order(right) visit 11 Hassan Khosravi / Geoffrey Tien 5

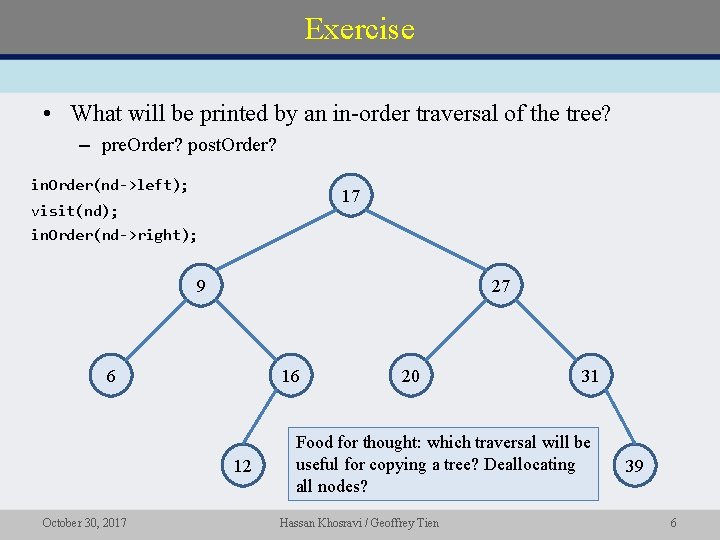
Exercise • What will be printed by an in-order traversal of the tree? – pre. Order? post. Order? in. Order(nd->left); 17 visit(nd); in. Order(nd->right); 9 27 6 16 12 October 30, 2017 20 31 Food for thought: which traversal will be useful for copying a tree? Deallocating all nodes? Hassan Khosravi / Geoffrey Tien 39 6

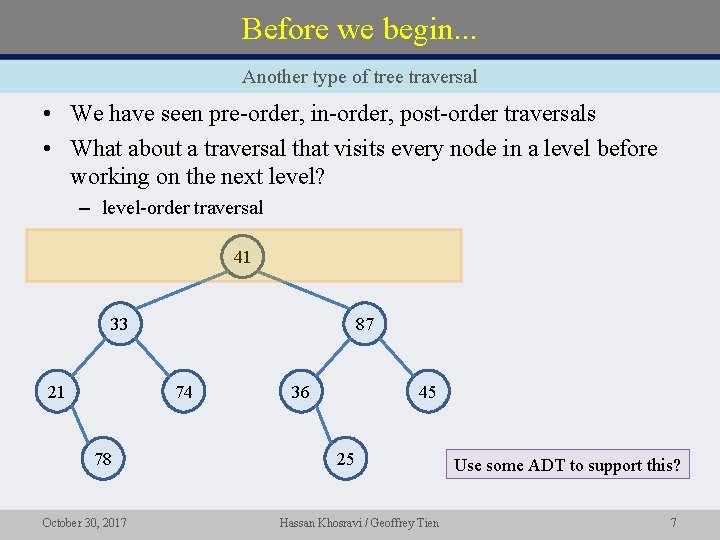
Before we begin. . . Another type of tree traversal • We have seen pre-order, in-order, post-order traversals • What about a traversal that visits every node in a level before working on the next level? – level-order traversal 41 33 21 87 74 78 October 30, 2017 36 45 25 Hassan Khosravi / Geoffrey Tien Use some ADT to support this? 7

Binary search trees A data structure for the Dictionary ADT? • A binary search tree is a binary tree with a special property – For all nodes in the tree: • All nodes in a left subtree have labels less than the label of the subtree's root • All nodes in a right subtree have labels greater than or equal to the label of the subtree's root • Binary search trees are fully ordered October 30, 2017 Hassan Khosravi / Geoffrey Tien 8

BST example 17 13 9 27 16 20 39 11 October 30, 2017 Hassan Khosravi / Geoffrey Tien 9

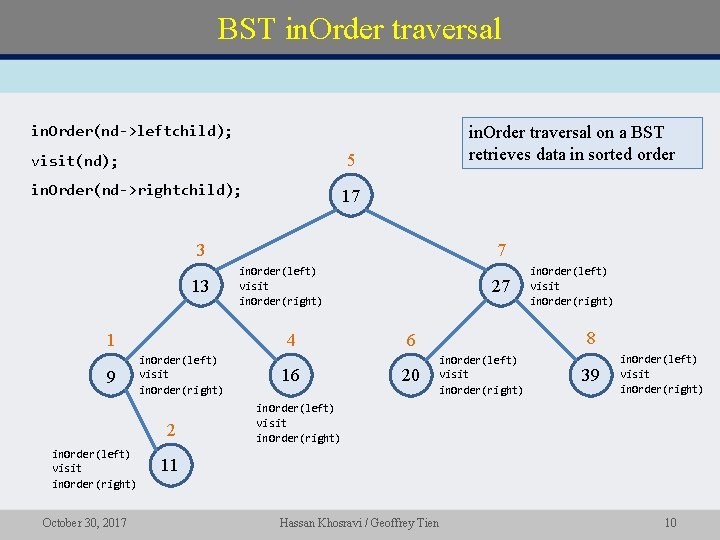
BST in. Order traversal in. Order(nd->leftchild); visit(nd); 5 in. Order(nd->rightchild); 17 in. Order traversal on a BST retrieves data in sorted order 3 13 in. Order(left) visit in. Order(right) 2 in. Order(left) visit in. Order(right) October 30, 2017 in. Order(left) visit in. Order(right) 4 1 9 7 16 27 8 6 20 in. Order(left) visit in. Order(right) 39 in. Order(left) visit in. Order(right) 11 Hassan Khosravi / Geoffrey Tien 10

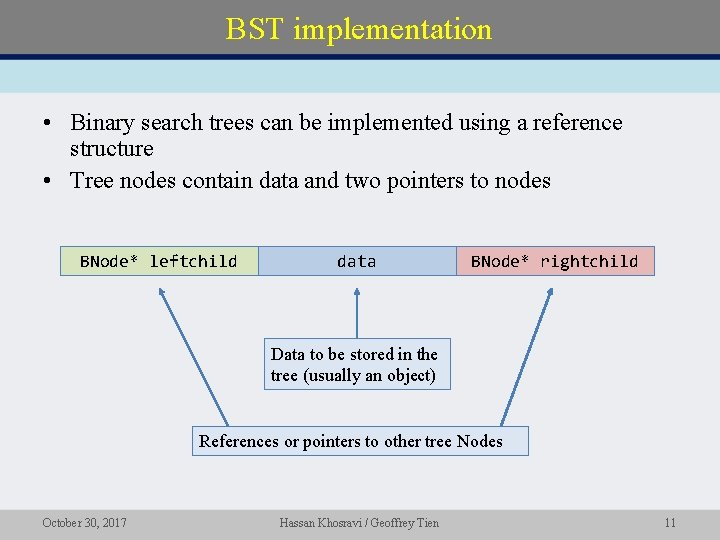
BST implementation • Binary search trees can be implemented using a reference structure • Tree nodes contain data and two pointers to nodes BNode* leftchild data BNode* rightchild Data to be stored in the tree (usually an object) References or pointers to other tree Nodes October 30, 2017 Hassan Khosravi / Geoffrey Tien 11

BST search • To find a value in a BST search from the root node: – If the target is less than the value in the node search its left subtree – If the target is greater than the value in the node search its right subtree – Otherwise return true, (or a pointer to the data, or …) • How many comparisons? – One for each node on the path – Worst case: height of the tree + 1 October 30, 2017 Hassan Khosravi / Geoffrey Tien 12

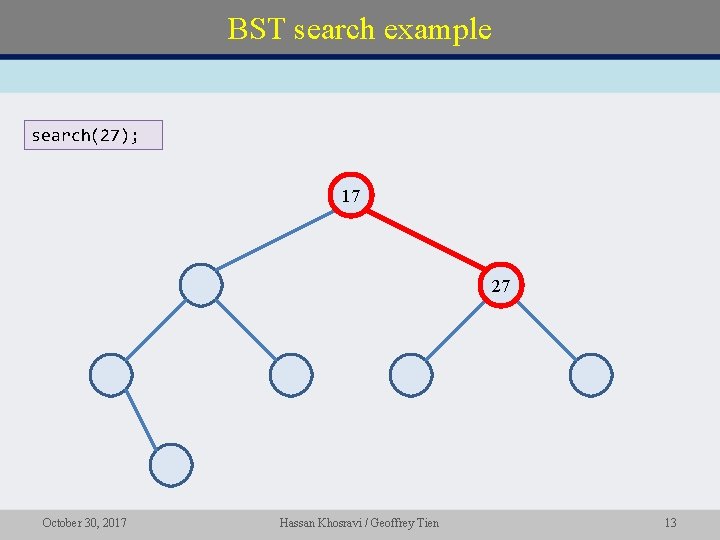
BST search example search(27); 17 27 October 30, 2017 Hassan Khosravi / Geoffrey Tien 13

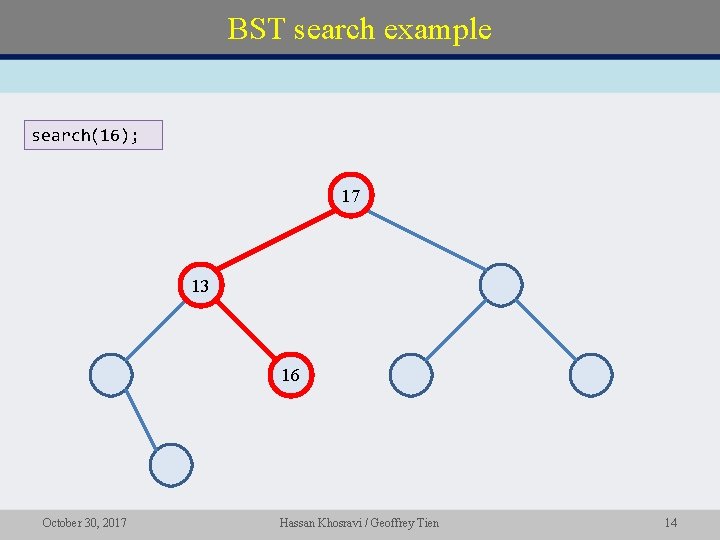
BST search example search(16); 17 13 16 October 30, 2017 Hassan Khosravi / Geoffrey Tien 14

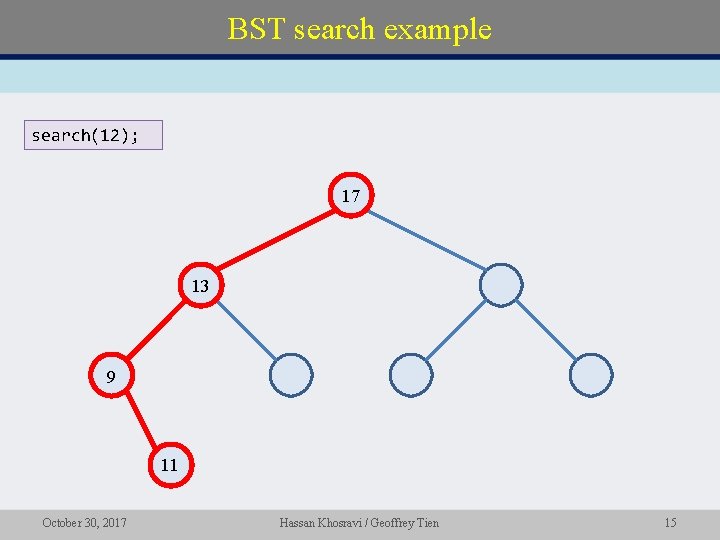
BST search example search(12); 17 13 9 11 October 30, 2017 Hassan Khosravi / Geoffrey Tien 15

Search implementation • Search can be implemented iteratively or recursively int search(BNode* nd, int key) { if (nd == NULL) return FALSE; else if (nd->data == key) return TRUE; else { if (key < nd->data) return search(nd->left, key); else return search(nd->right, key); } } October 30, 2017 Hassan Khosravi / Geoffrey Tien 16

BST insertion • The BST property must hold after insertion • Therefore the new node must be inserted in the correct position – This position is found by performing a search – If the search ends at the (null) left child of a node make its left child refer to the new node – If the search ends at the right child of a node make its right child refer to the new node • The cost is about the same as the cost for the search algorithm, O(height) October 30, 2017 Hassan Khosravi / Geoffrey Tien 17

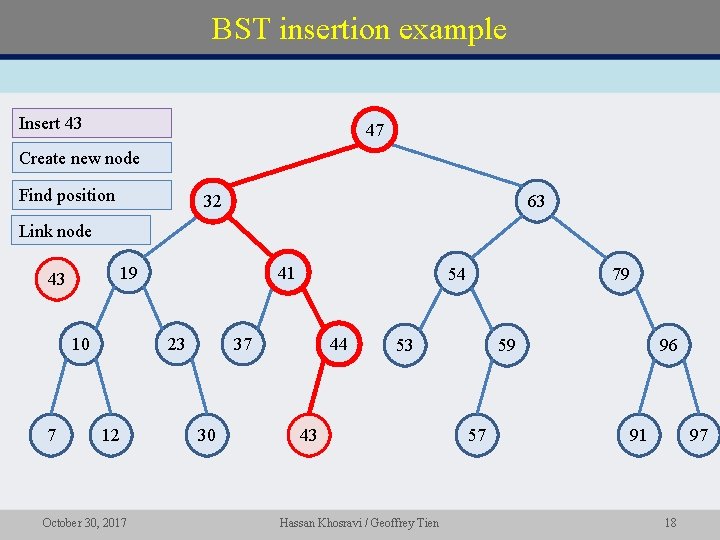
BST insertion example Insert 43 47 Create new node Find position 32 63 Link node 19 43 10 7 41 23 12 October 30, 2017 54 37 30 44 79 53 43 Hassan Khosravi / Geoffrey Tien 59 57 96 91 97 18

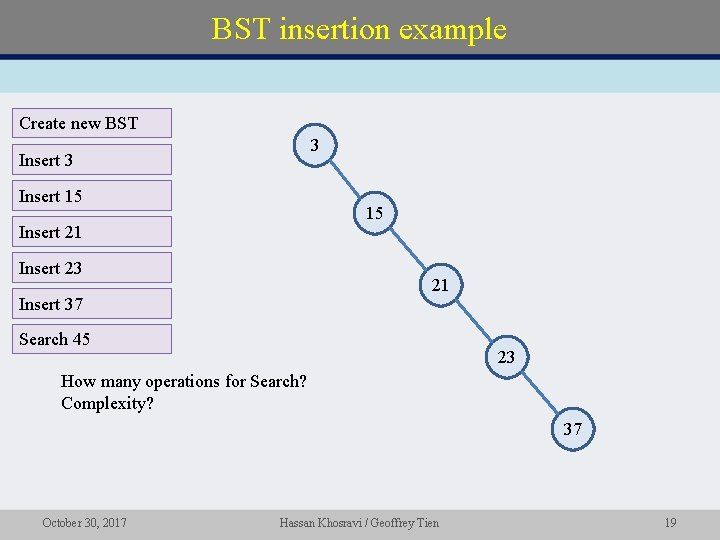
BST insertion example Create new BST 3 Insert 15 15 Insert 21 Insert 23 21 Insert 37 Search 45 23 How many operations for Search? Complexity? 37 October 30, 2017 Hassan Khosravi / Geoffrey Tien 19

Insert implementation • Insert can also be implemented iteratively or recursively BNode* insert(BNode* nd, int key) { if (nd == NULL) { BNode* newnode = (BNode*) malloc(sizeof(BNode)); newnode->data = key; newnode->left = NULL; newnode->right = NULL; return newnode; } else { if (key < nd->data) nd->left = insert(nd->left, key); else nd->right = insert(nd->right, key); return nd; } } October 30, 2017 Hassan Khosravi / Geoffrey Tien 20

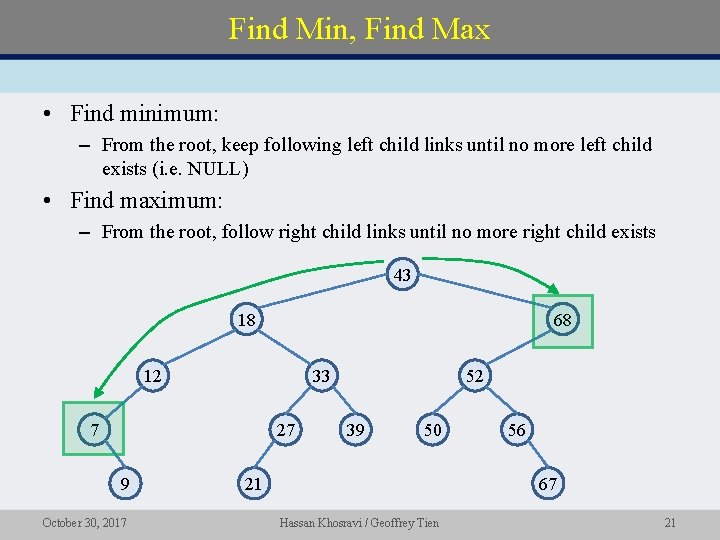
Find Min, Find Max • Find minimum: – From the root, keep following left child links until no more left child exists (i. e. NULL) • Find maximum: – From the root, follow right child links until no more right child exists 43 18 68 12 33 7 27 9 October 30, 2017 52 39 50 21 56 67 Hassan Khosravi / Geoffrey Tien 21

Exercise • Write iterative implementations for: – // returns TRUE or FALSE int search(BNode* nd, int key) – // returns the root of the subtree receiving the // inserted item BNode* insert(BNode* nd, int key) • Write iterative implementations for: – // returns the value of the minimum key int find. Min(BNode* nd) – // returns the value of the maximum key int find. Max(BNode* nd) October 30, 2017 Hassan Khosravi / Geoffrey Tien 22

Readings for this lesson • Thareja – Chapter 9. 4 – 10. 1 – 10. 2. 2, 10. 2. 4 – 10. 2. 5, 10. 2. 8 – 10. 2. 9 • Next class: – Thareja Chapter 10. 2. 3 October 30, 2017 Hassan Khosravi / Geoffrey Tien 23