Binary Search Trees Implementation and Operations BST 17

Binary Search Trees Implementation and Operations BST 17 Soft. Uni Team 9 Technical Trainers Software University http: //softuni. bg 6 19 12 25

Table of Contents 1. Binary Search Trees 2. BST Operations § Search() § Delete. Min() § Range() 2

Have a Question? sli. do #Ds. Algo 3

Binary Search Trees Two Children at Most

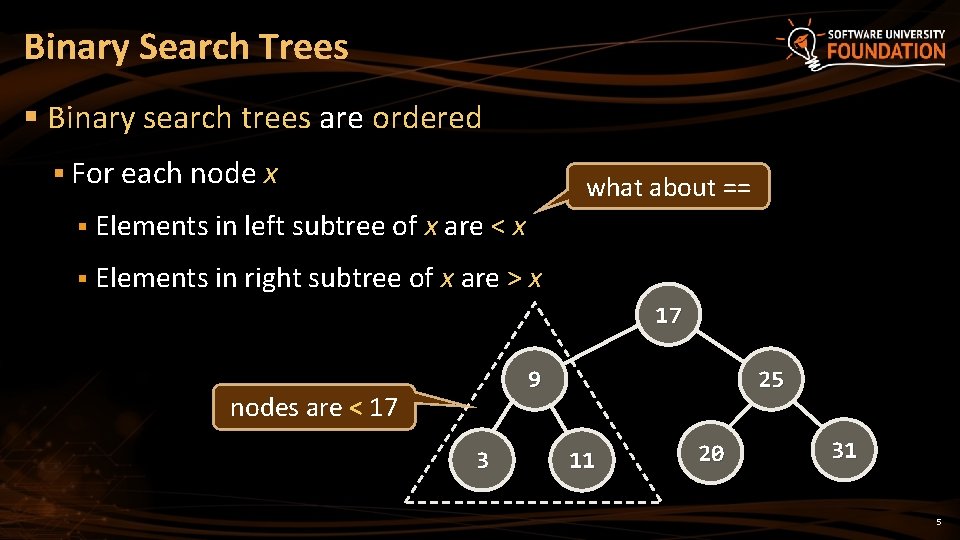
Binary Search Trees § Binary search trees are ordered § For each node x what about == § Elements in left subtree of x are < x § Elements in right subtree of x are > x 17 9 nodes are < 17 3 25 11 20 31 5

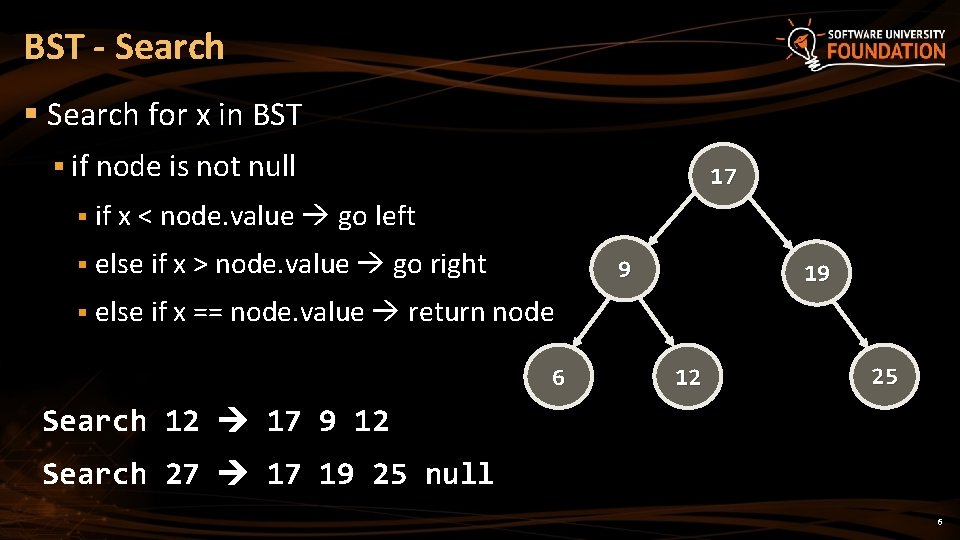
BST - Search § Search for x in BST § if node is not null 17 § if x < node. value go left § else if x > node. value go right 9 19 § else if x == node. value return node 6 12 25 Search 12 17 9 12 Search 27 17 19 25 null 6

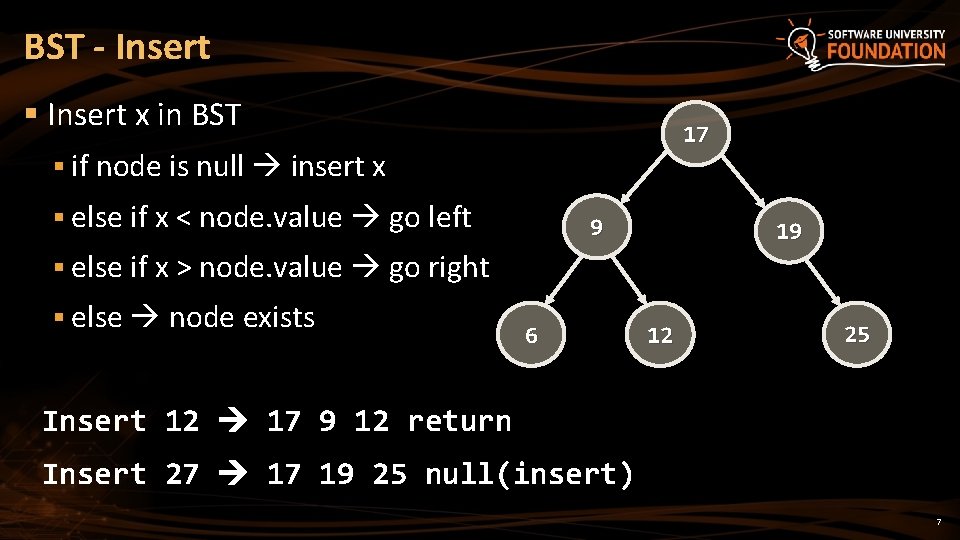
BST - Insert § Insert x in BST 17 § if node is null insert x § else if x < node. value go left 9 19 § else if x > node. value go right § else node exists 6 12 25 Insert 12 17 9 12 return Insert 27 17 19 25 null(insert) 7

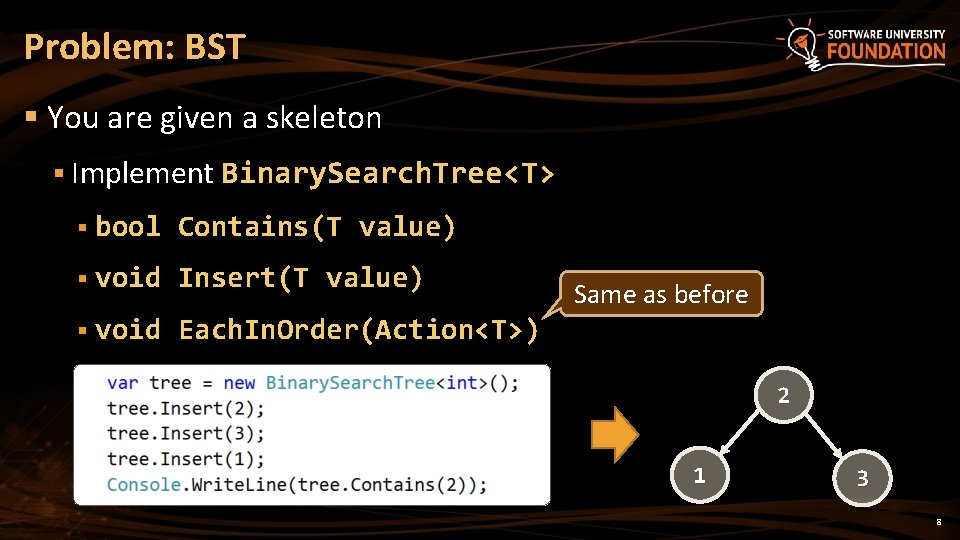
Problem: BST § You are given a skeleton § Implement Binary. Search. Tree<T> § bool Contains(T value) § void Insert(T value) § void Each. In. Order(Action<T>) Same as before 2 1 3 8

Solution: BST Node Inside BST private Node root; private class Node { public Node(T value) { this. Value = value; } } public T Value { get; set; } Node Left { get; set; } Node Right { get; set; } 9

Solution: BST Contains public bool Contains(T value) { Node current = this. root; while (current != null) { if (value. Compare. To(current. Value) < 0) current = current. Left; else if (value. Compare. To(current. Value) > 0) current = current. Right; else break; } return current != null; } 10

Solution: BST Insert public void Insert(T value) { if (this. root == null) { this. root = new Node(value); } return; Node parent = null; Node current = this. root; while(current != null) { //TODO: search for node } } //TODO: insert node 11

Problem: BST Search § Implement: § BST<T> Search(T value) § Make sure the method works for: § empty tree § tree with one element § tree with two elements - root + left/right § tree with multiple elements 12

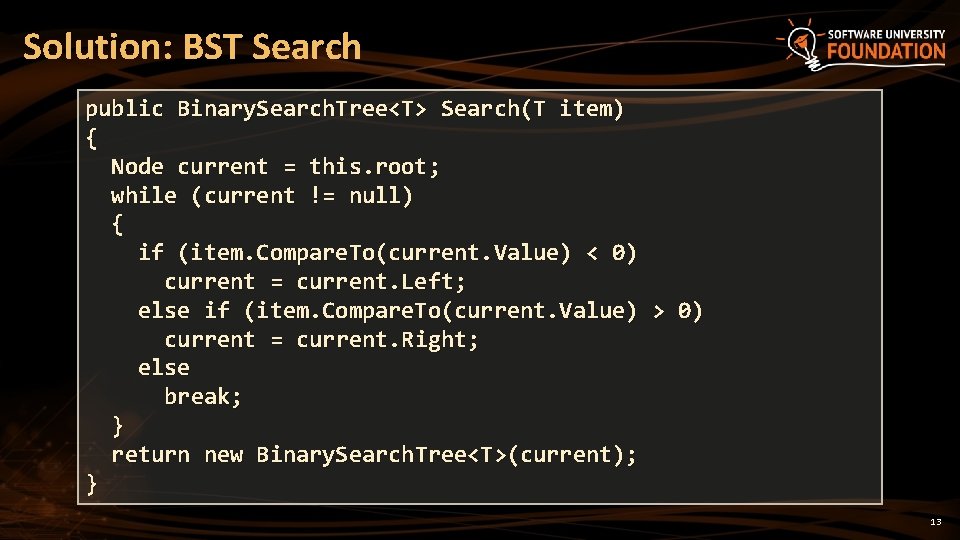
Solution: BST Search public Binary. Search. Tree<T> Search(T item) { Node current = this. root; while (current != null) { if (item. Compare. To(current. Value) < 0) current = current. Left; else if (item. Compare. To(current. Value) > 0) current = current. Right; else break; } return new Binary. Search. Tree<T>(current); } 13

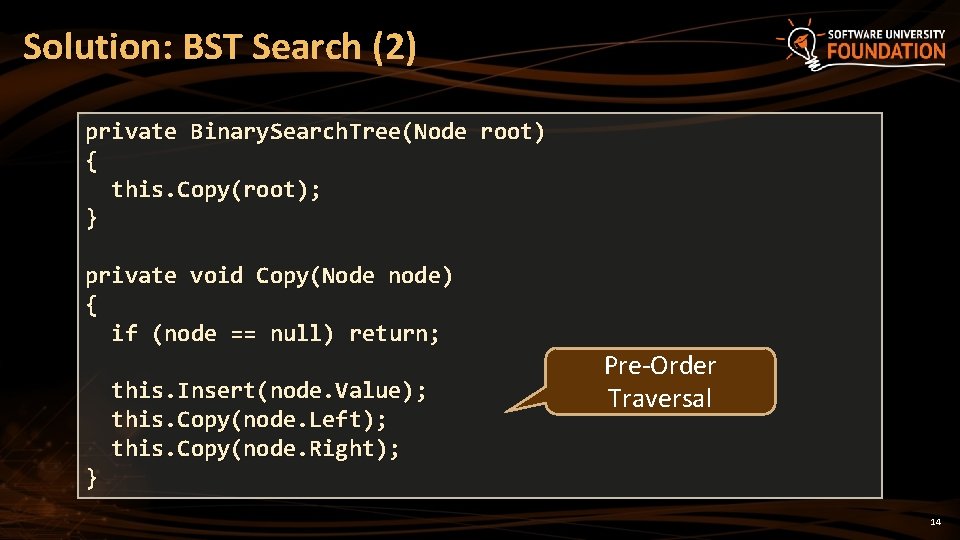
Solution: BST Search (2) private Binary. Search. Tree(Node root) { this. Copy(root); } private void Copy(Node node) { if (node == null) return; } this. Insert(node. Value); this. Copy(node. Left); this. Copy(node. Right); Pre-Order Traversal 14

Lab Exercise BST - Insert, Contains, Search

BST - Search Operation Speed - Quiz TIME’S UP! TIME: § What is the speed of the Search(T) operation on BST? § O(n) § O(log(n)) § O(1) 16

BST - Search Operation Speed - Answer § What is the speed of the Search() operation on BST? § O(n) § O(log(n)) § O(1) 17 19 25 34 17

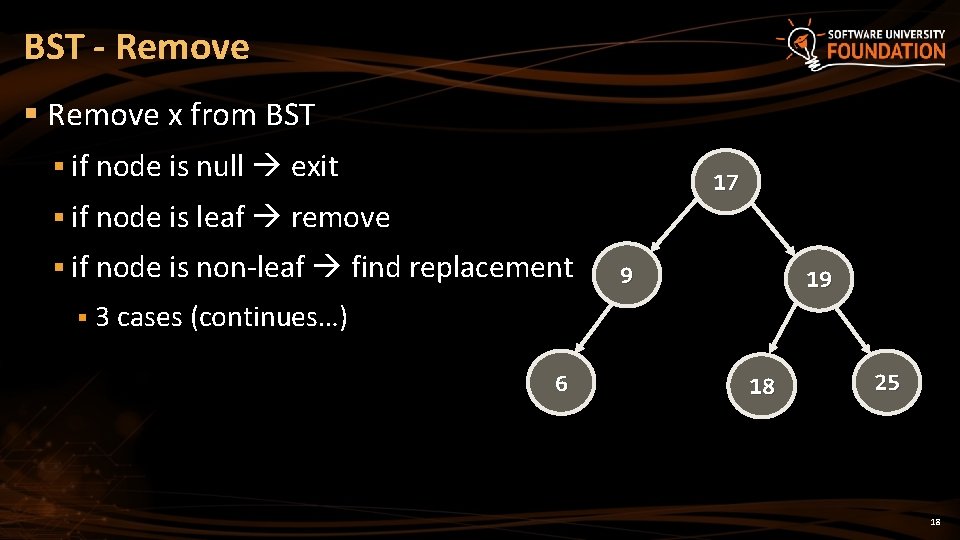
BST - Remove § Remove x from BST § if node is null exit 17 § if node is leaf remove § if node is non-leaf find replacement 9 19 § 3 cases (continues…) 6 18 25 18

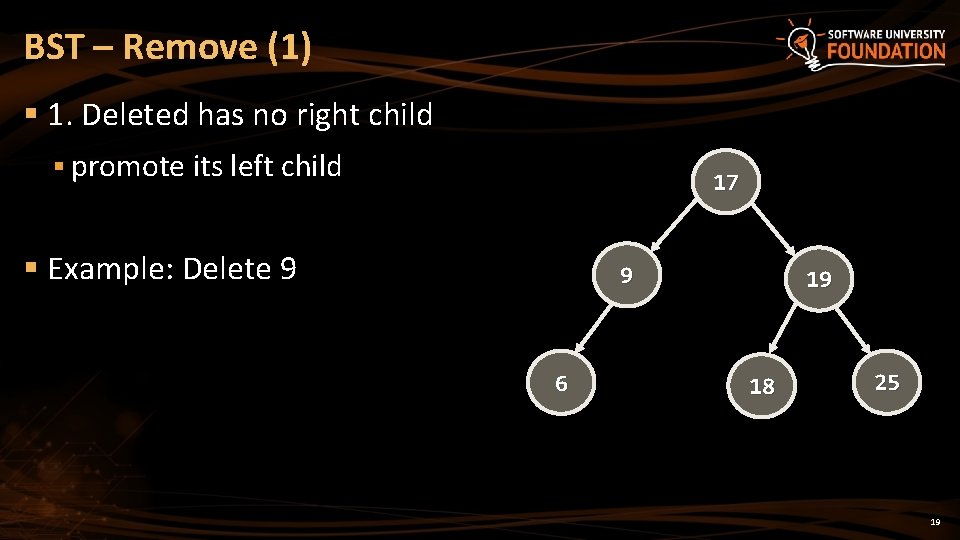
BST – Remove (1) § 1. Deleted has no right child § promote its left child 17 § Example: Delete 9 9 6 19 18 25 19

BST – Remove (2) § 2. Deleted right's child has no left child § promote right child 17 § Example: Delete 19 9 6 19 25 18 null 20

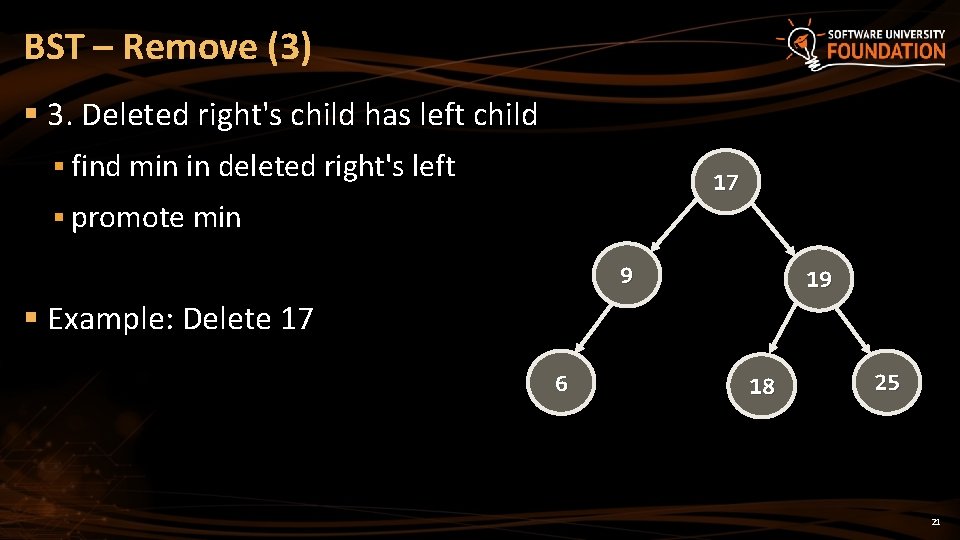
BST – Remove (3) § 3. Deleted right's child has left child § find min in deleted right's left 17 § promote min 9 19 § Example: Delete 17 6 18 25 21

Problem: BST Delete Min § Implement: § void Delete. Min() § Make sure the method works for: § empty tree § tree with one element § tree with two elements - root + left/right § tree with multiple elements 22

Solution: BST Delete Min public void Delete. Min() { if (this. root == null) { return; } Node<T> parent = null; Node<T> current = this. root; while (current. Left != null) { parent = current; current = parent. Left; } } if (parent == null) { this. root = current. Right; } else { parent. Left = current. Right; } 23

Lab Exercise BST - Delete. Min

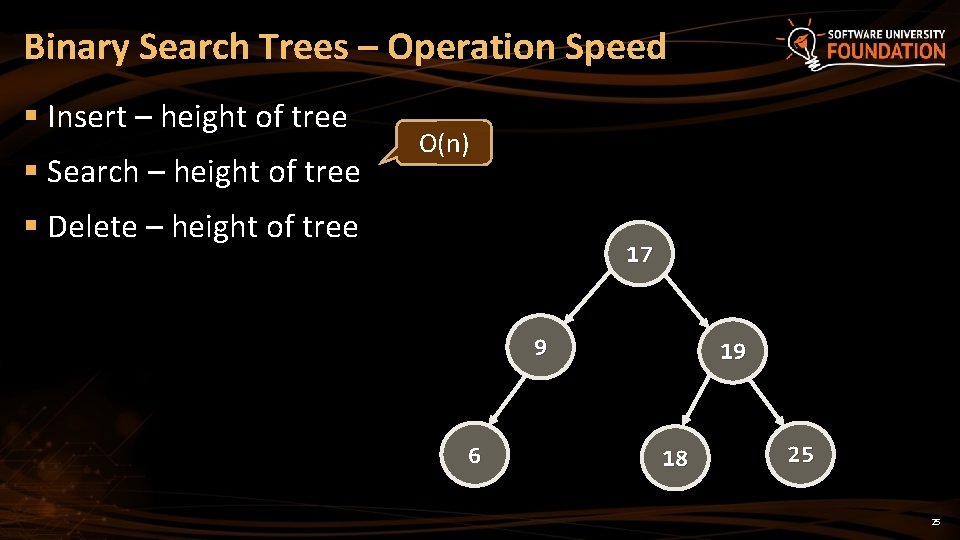
Binary Search Trees – Operation Speed § Insert – height of tree § Search – height of tree O(n) § Delete – height of tree 17 9 6 19 18 25 25

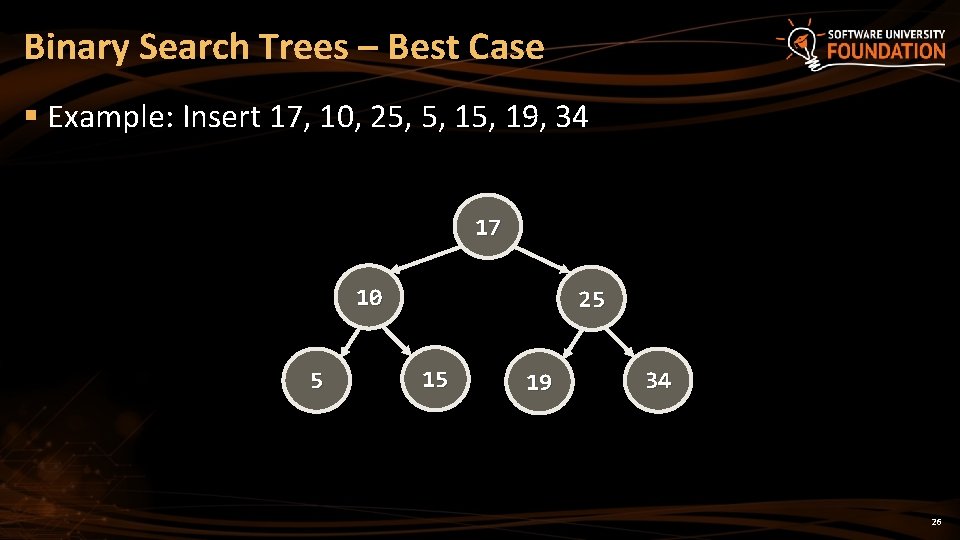
Binary Search Trees – Best Case § Example: Insert 17, 10, 25, 5, 19, 34 17 10 5 25 15 19 34 26

Binary Search Trees – Average Case § You can insert values in ever random order § Example: Insert 17, 19, 9, 6, 25, 28, 18 17 9 6 19 18 25 28 27

Binary Search Trees – Worst Case § You can insert values in ever increasing/decreasing order § Example: Insert 17, 19, 25, 34 17 Linked List 19 25 34 28

Balanced Binary Search Trees § Binary search trees can be balanced § Balanced trees have for each node § Nearly equal number of nodes in its subtrees § Balanced trees have height of ~ log(n) 29

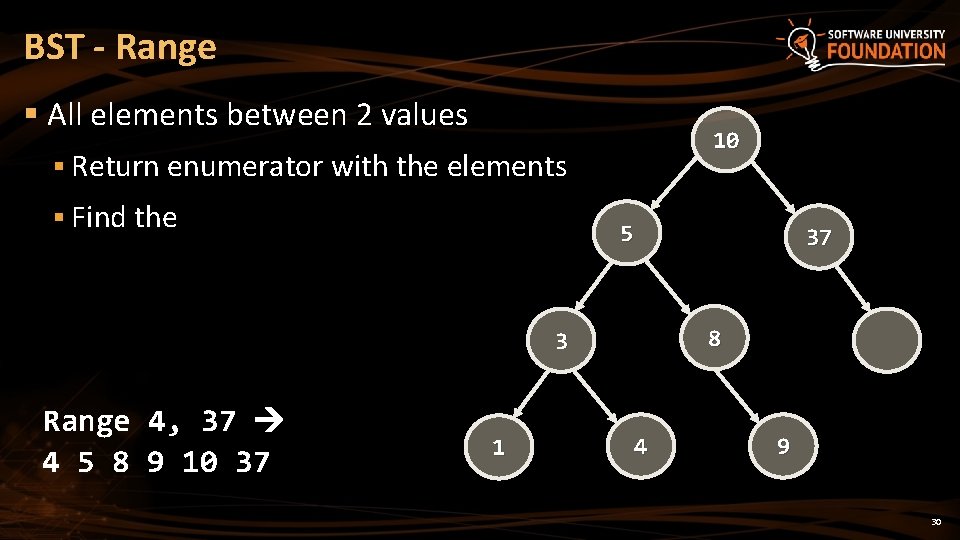
BST - Range § All elements between 2 values 10 § Return enumerator with the elements § Find the 5 8 3 Range 4, 37 4 5 8 9 10 37 1 37 4 9 30

Lab Exercise BST - Range

BST - Range Operation Speed - Quiz TIME’S UP! TIME: § What is the speed of the Range(T, T) operation on BST? § O(n) § O(log(n)) § O(1) 32

BST - Range Operation Speed - Answer § What is the speed of the Range(T, T) operation on BST? § O(n) § O(log(n)) § O(1) 33

Summary § Binary search trees are ordered binary trees § Balanced trees have roughly the same height of their left and right children 34

Binary Search Trees ? s n stio e u Q ? ? ? https: //softuni. bg/opencourses/data-structures

License § This course (slides, examples, labs, videos, homework, etc. ) is licensed under the "Creative Commons Attribution. Non. Commercial-Share. Alike 4. 0 International" license § Attribution: this work may contain portions from § "Fundamentals of Computer Programming with C#" book by Svetlin Nakov & Co. under CC-BY-SA license § "Data Structures and Algorithms" course by Telerik Academy under CC-BY-NC-SA license 36

Trainings @ Software University (Soft. Uni) § Software University – High-Quality Education, Profession and Job for Software Developers § softuni. bg § Software University Foundation § softuni. org § Software University @ Facebook § facebook. com/Software. University § Software University Forums § forum. softuni. bg