Binary Search Trees A binary tree No node

Binary Search Trees • A binary tree: – No node has more than two child nodes (called child subtrees). – Child subtrees must be differentiated, into: • Left-child subtree • Right-child subtree • A search tree: – For every node, p: • All nodes in the left subtree are < p • All nodes in the right subtree are > p

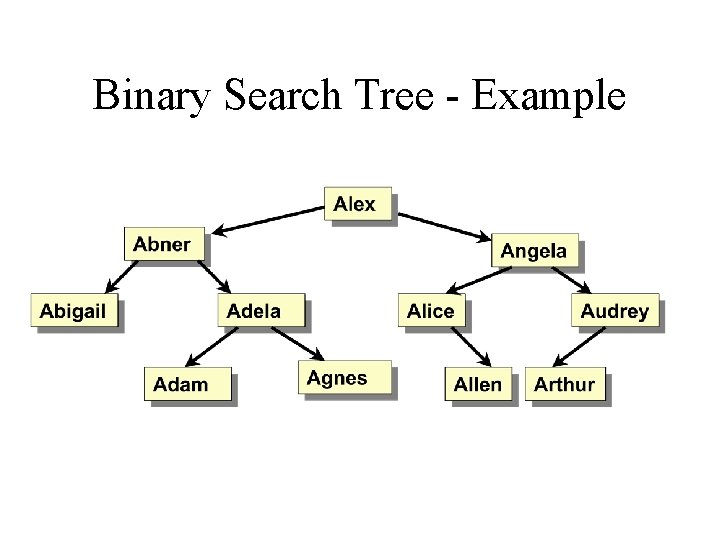
Binary Search Tree - Example

Binary Search Trees (cont) • Searching for a value is in a tree of N nodes is: – O(log N) if the tree is “balanced” – O(N) if the tree is “unbalanced”

“Unbalanced” Binary Search Trees • Below is a binary search tree that is NOT “balanced”

Properties of Binary Trees • A binary tree is a full binary tree if and only if: – Each non leaf node has exactly two child nodes – All leaf nodes have identical path length • It is called full since all possible node slots are occupied

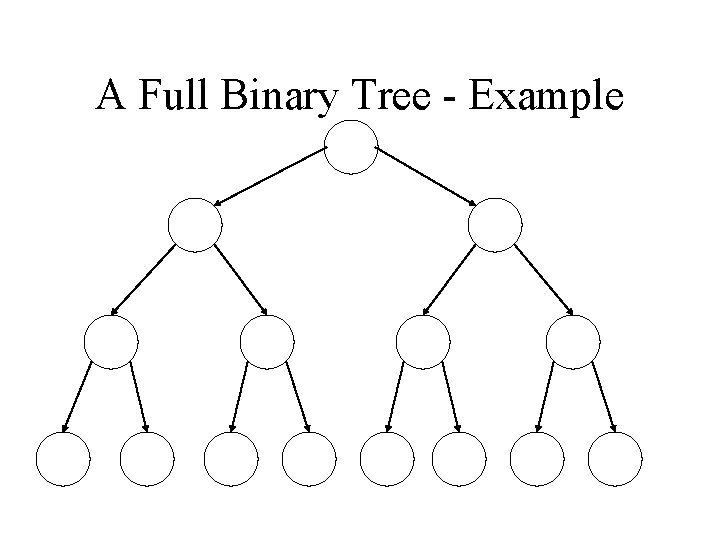
A Full Binary Tree - Example

Full Binary Trees • A Full binary tree of height h will have how many leaves? leaves • A Full binary tree of height h will have how many nodes? nodes

Complete Binary Trees • A complete binary tree (of height h) satisfies the following conditions: – Level 0 to h-1 represent a full binary tree of height h-1 – One or more nodes in level h-1 may have 0, or 1 child nodes – If j, k are nodes in level h-1, then j has more child nodes than k if and only if j is to the left of k

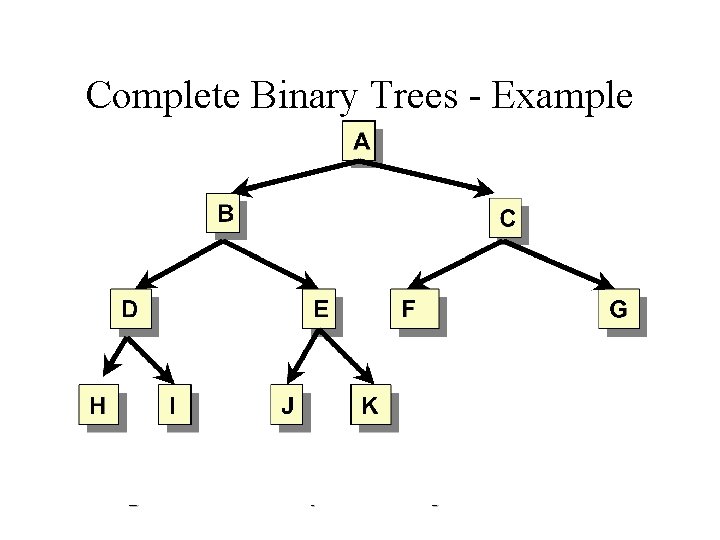
Complete Binary Trees - Example

Complete Binary Trees (cont) • Given a set of N nodes, a complete binary tree of these nodes provides the maximum number of leaves with the minimal average path length (per node) • The complete binary tree containing n nodes must have at least one path from root to leaf of length log n

Height-balanced Binary Tree • A height-balanced binary tree is a binary tree such that: – The left & right subtrees for any given node differ in height by no more than one • Note: Each complete binary tree is a heightbalanced binary tree

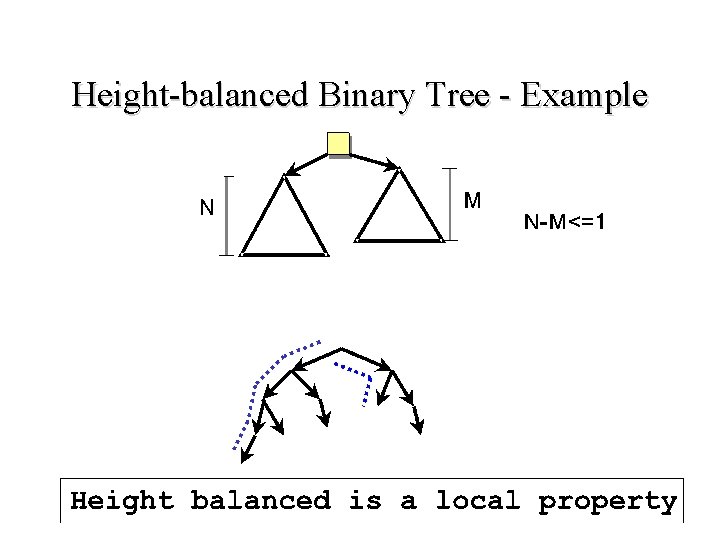
Height-balanced Binary Tree - Example

Advantages of Height-balanced Binary Trees • Height-balanced binary trees are “balanced” • Operations that run in time proportional to the height of the tree are O(log n), n the number of nodes with limited performance variance • Variance is a very important concern in real time applications, e. g. connecting calls in a telephone network