Binary Search Trees 15 Data Structures Algorithms 3

Binary Search Trees 15 Data Structures & Algorithms 3 9 20

Abstract Data Type: Dynamic Ordered Sets Stores a set S of elements, each with an associated key. Two types of operations: • queries • modifying operations return information about the order change the set Common queries Search, Minimum, Maximum, Successor, Predecessor Common modifying operations Insert, Delete

Data Structure: Binary search trees p
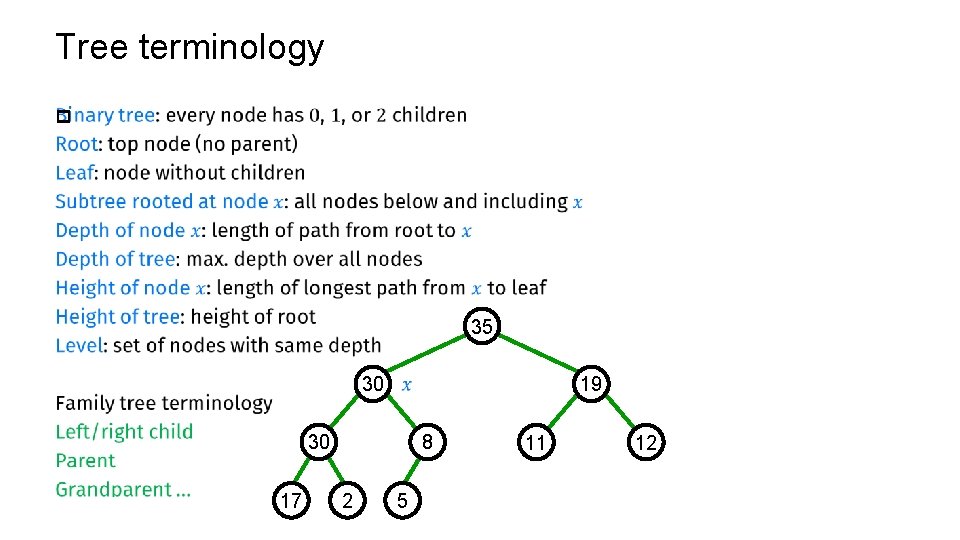
Tree terminology p 35 30 19 30 17 8 2 5 11 12
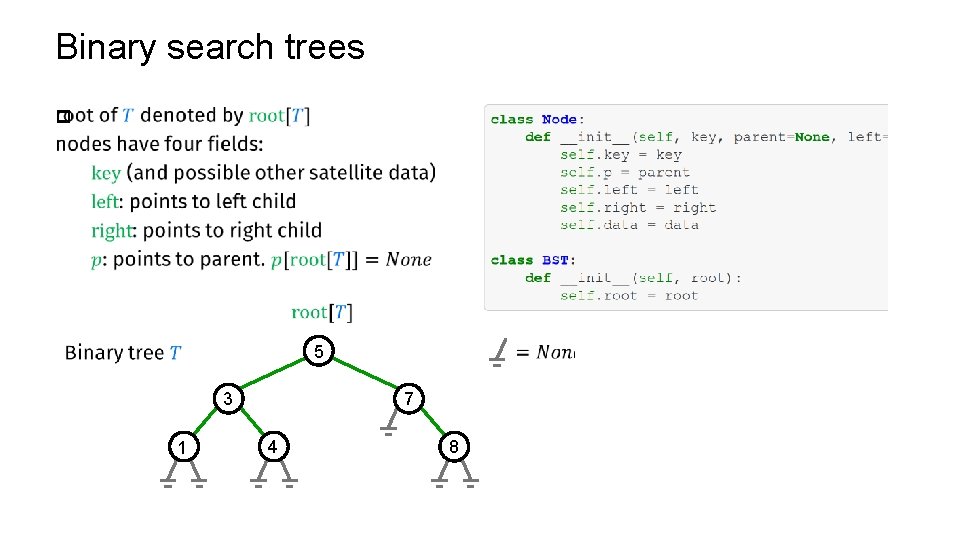
Binary search trees p 5 3 1 7 4 8

Binary search trees p 5 3 1 7 4 8
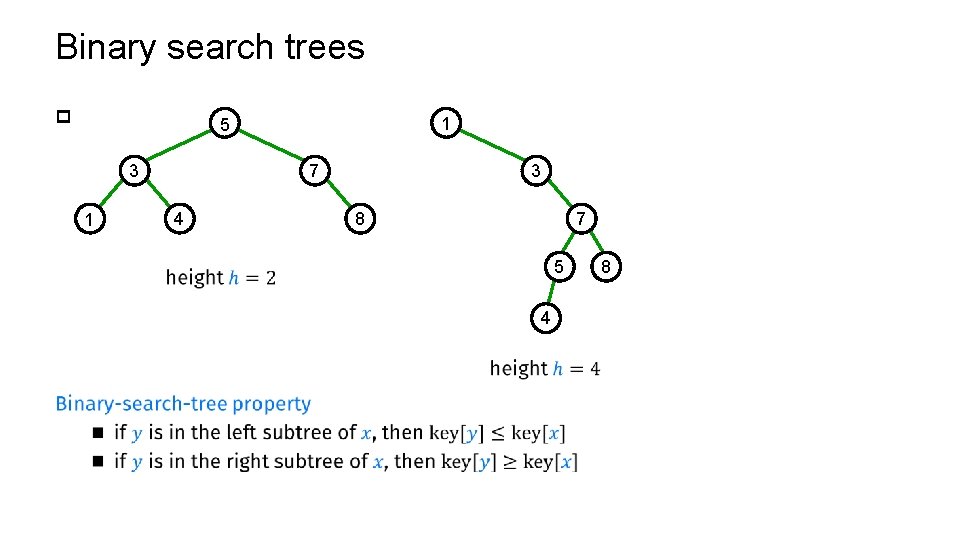
Binary search trees p 1 5 3 1 3 7 4 7 8 5 4 8
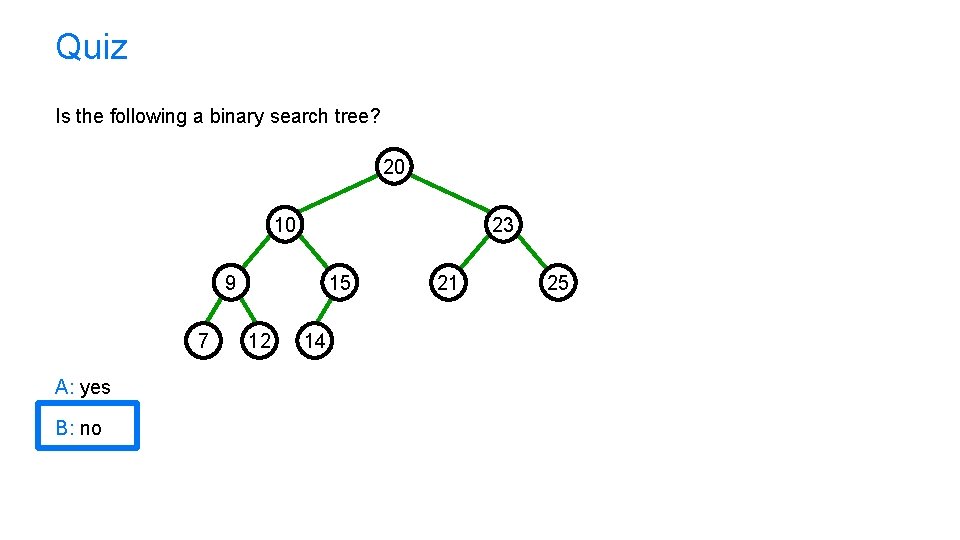
Quiz Is the following a binary search tree? 20 10 23 9 7 A: yes B: no 15 12 14 21 25
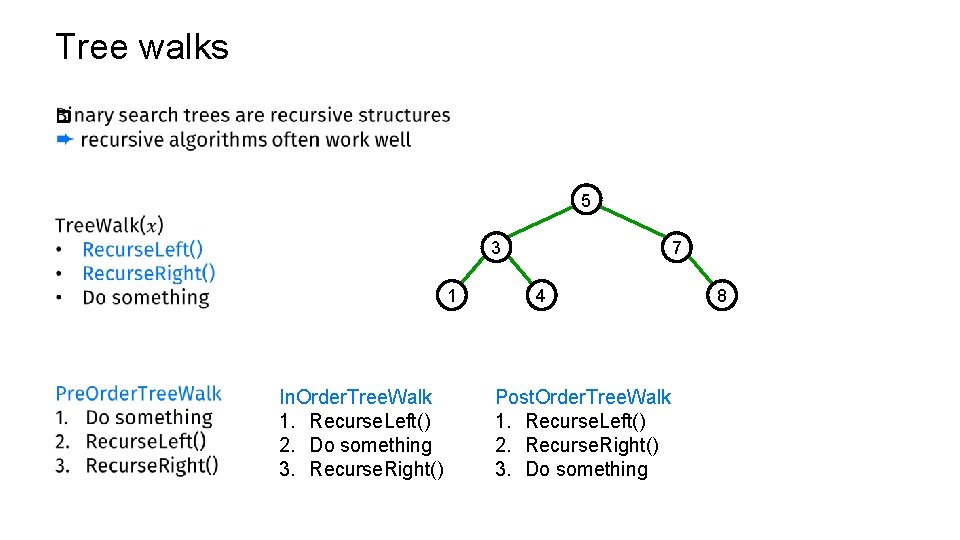
Tree walks p 5 3 1 In. Order. Tree. Walk 1. Recurse. Left() 2. Do something 3. Recurse. Right() 7 4 Post. Order. Tree. Walk 1. Recurse. Left() 2. Recurse. Right() 3. Do something 8
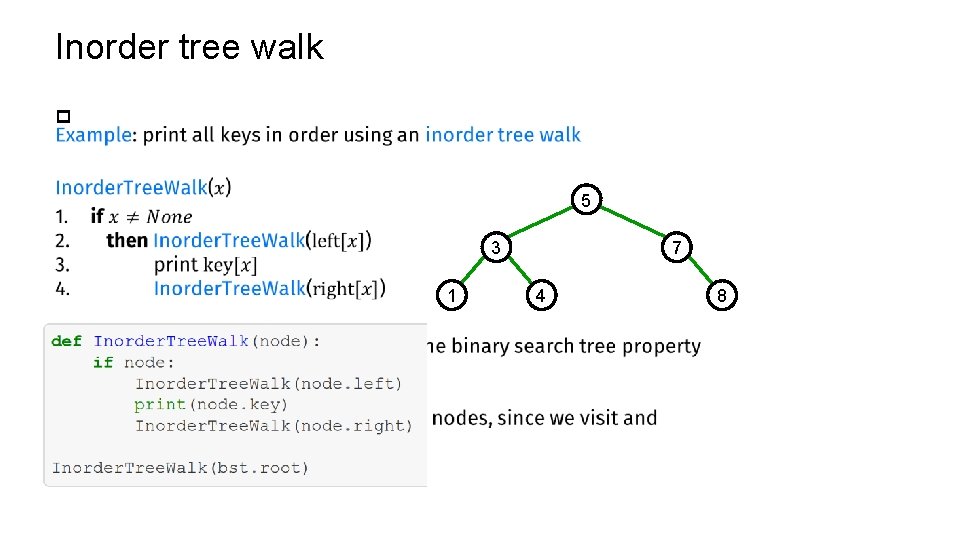
Inorder tree walk p 5 3 1 7 4 8

Inorder tree walk p

T(Inorder tree walk) = O(n) p

Quiz p

Queries
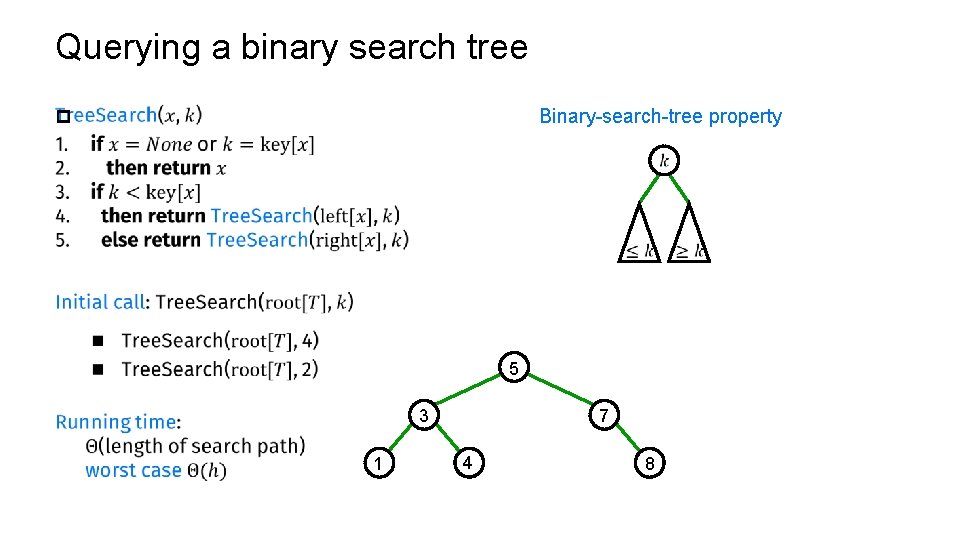
Querying a binary search tree Binary-search-tree property p 5 3 1 7 4 8
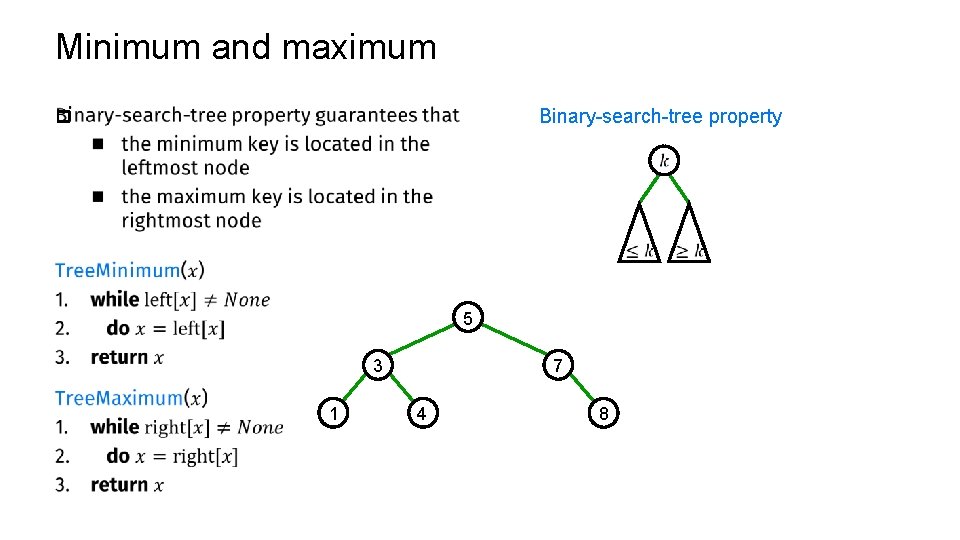
Minimum and maximum Binary-search-tree property p 5 3 1 7 4 8
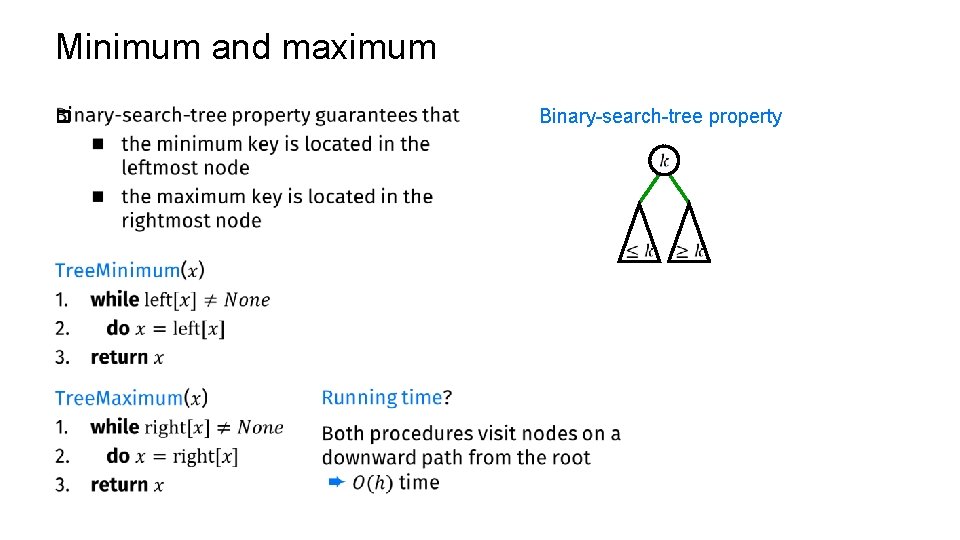
Minimum and maximum p Binary-search-tree property

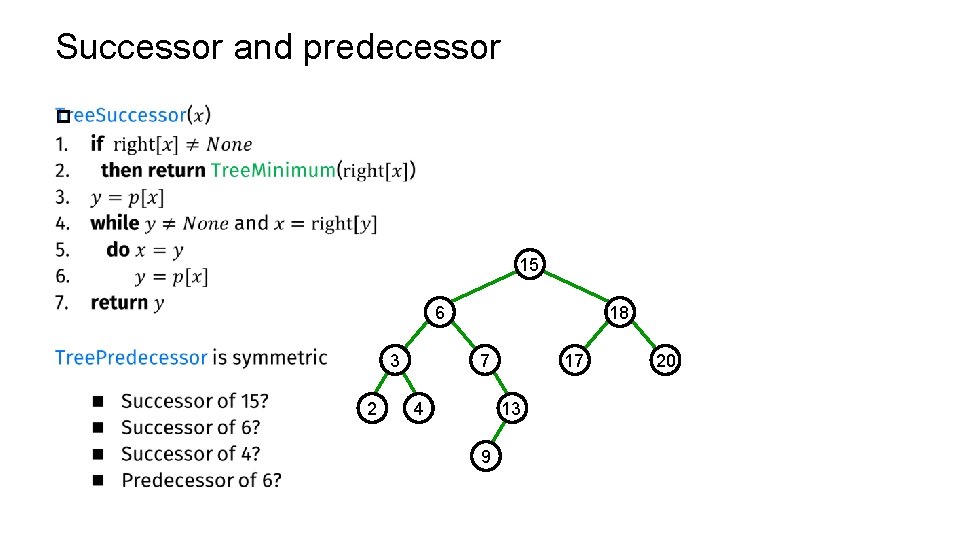
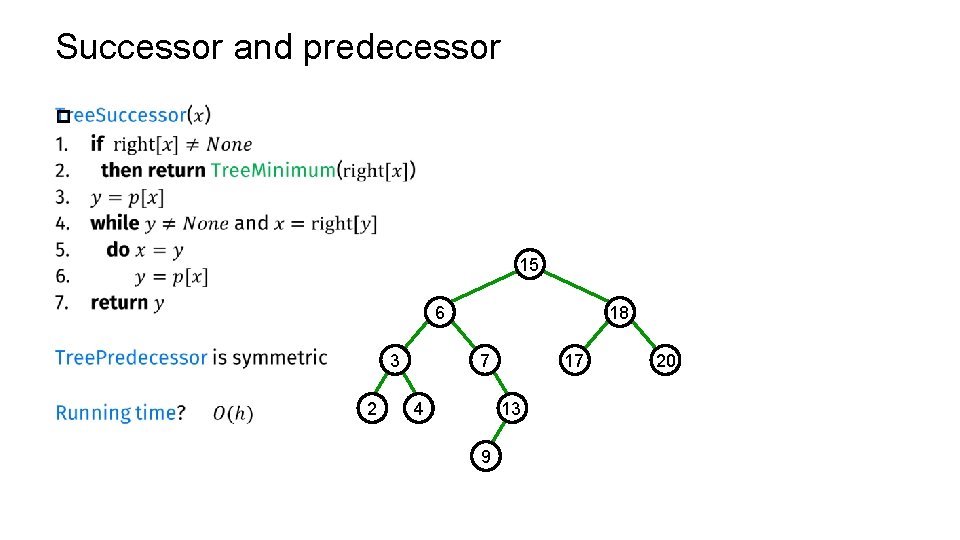
Successor and predecessor p

Successor and predecessor p
Successor and predecessor p 15 6 7 3 2 18 4 17 13 9 20
Successor and predecessor p 15 6 7 3 2 18 4 17 13 9 20
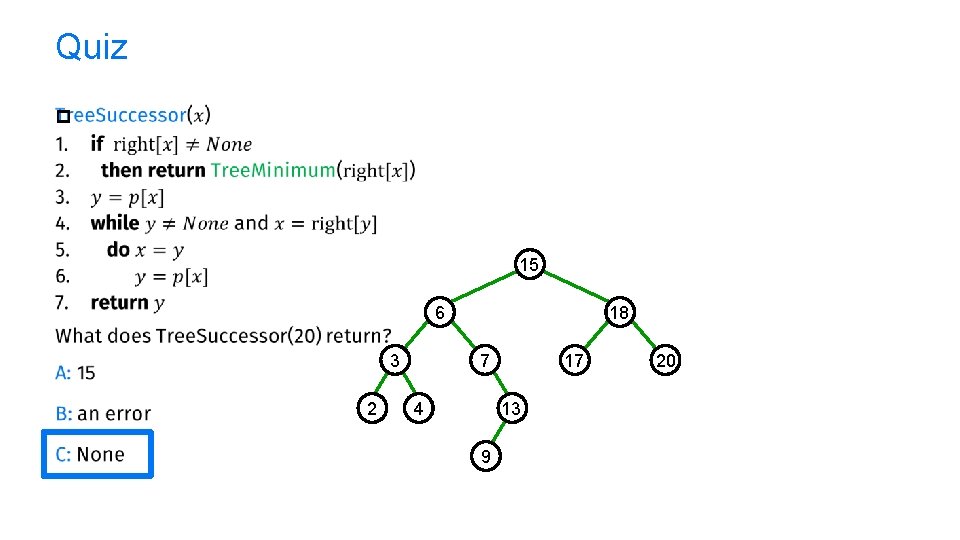
Quiz p 15 6 7 3 2 18 4 17 13 9 20

Insert and Delete
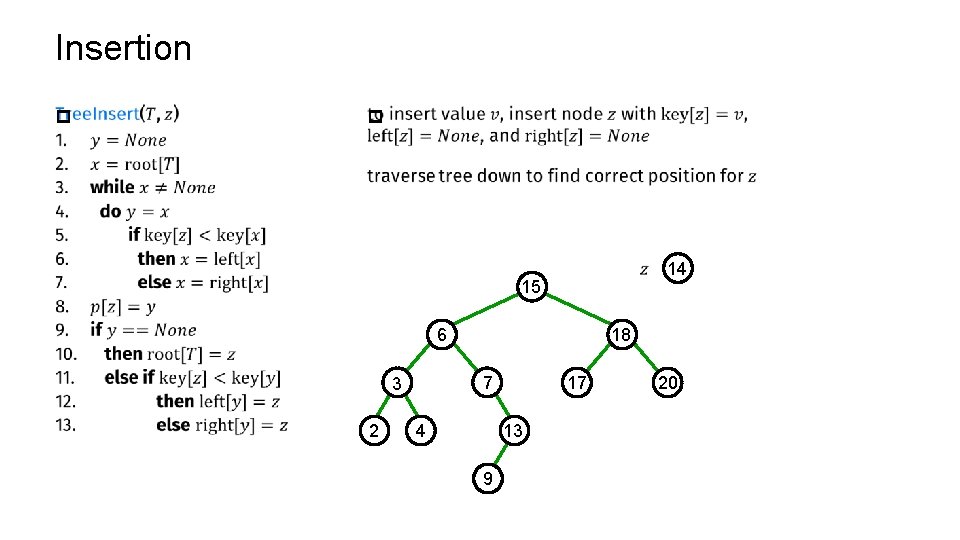
Insertion p p 14 15 6 7 3 2 18 4 17 13 9 20
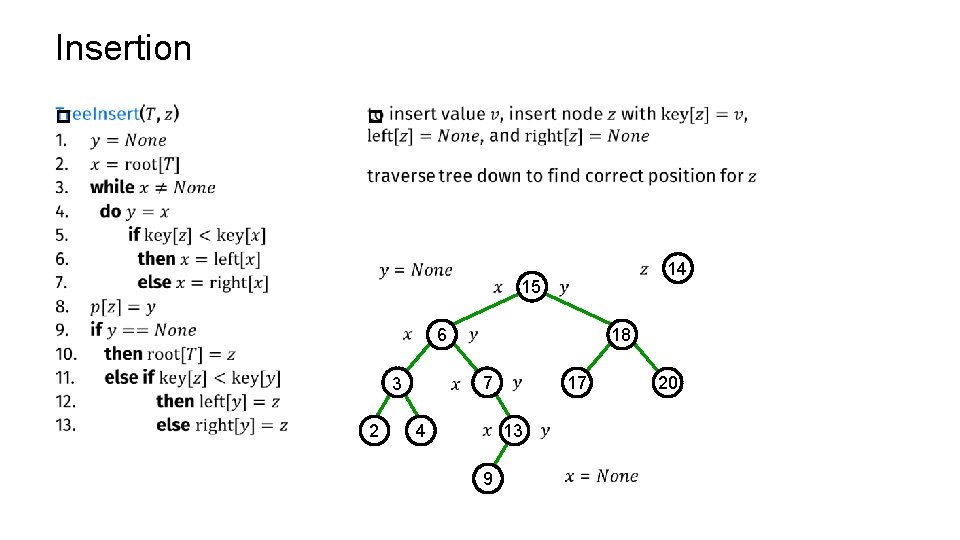
Insertion p p 14 15 6 7 3 2 18 4 17 13 9 20
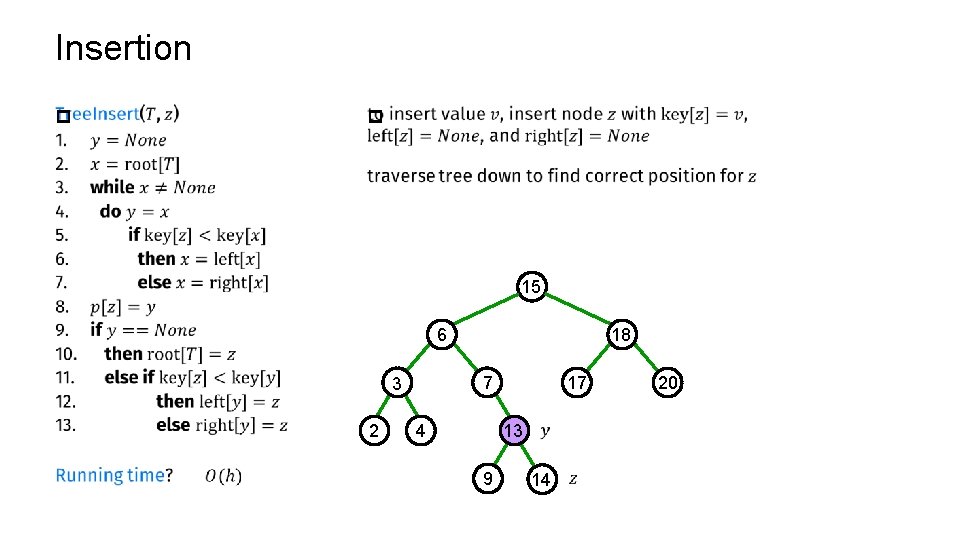
Insertion p p 15 6 7 3 2 18 4 17 13 9 14 20
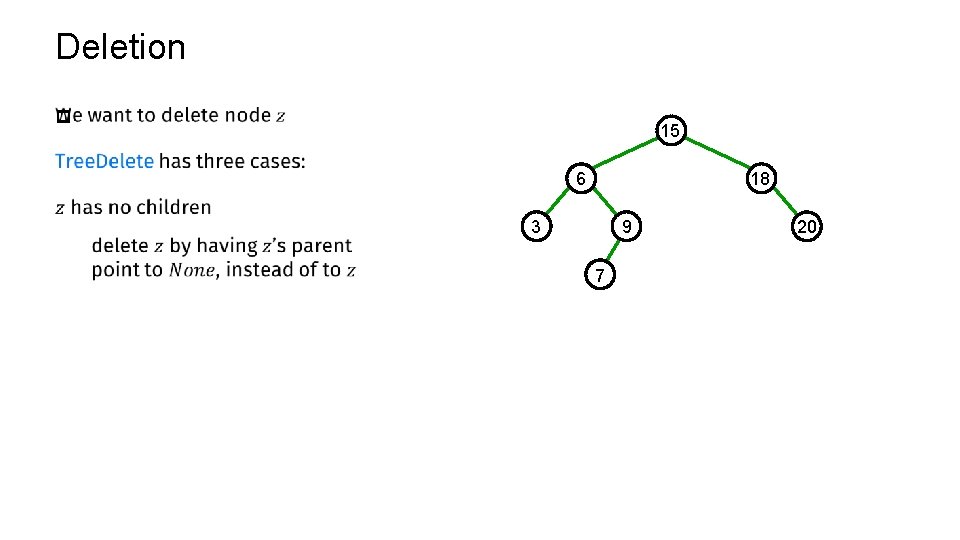
Deletion p 15 6 18 9 3 7 20
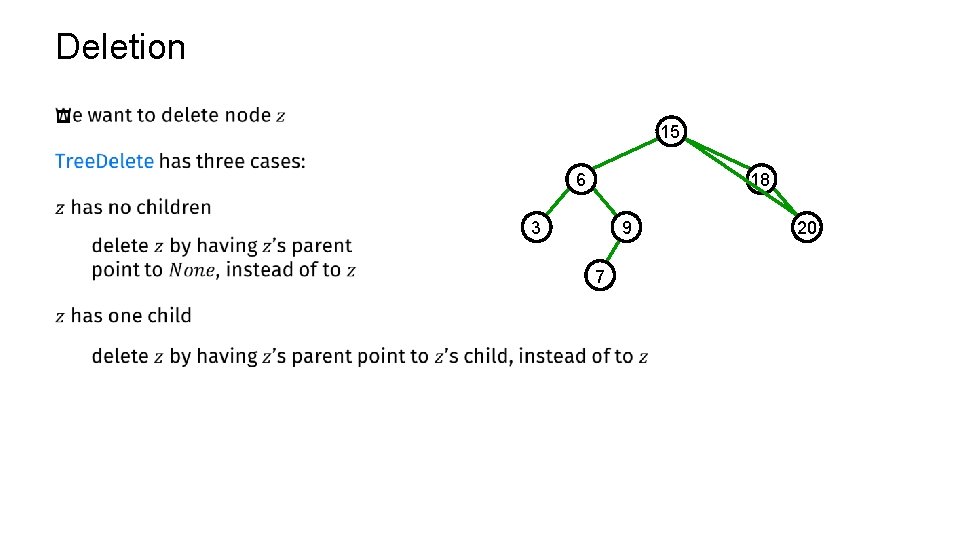
Deletion p 15 6 18 9 3 7 20
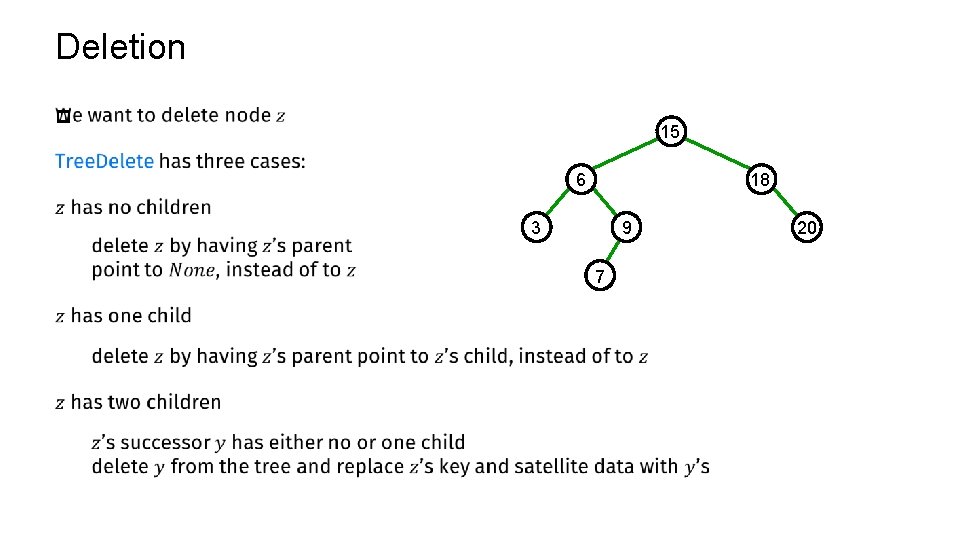
Deletion p 15 6 18 9 3 7 20
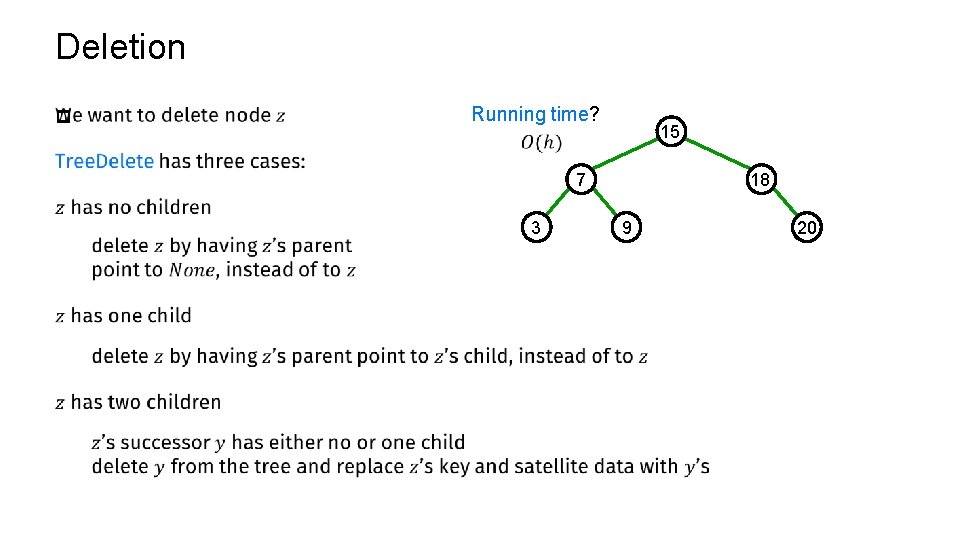
Deletion p Running time? 15 7 3 18 9 20
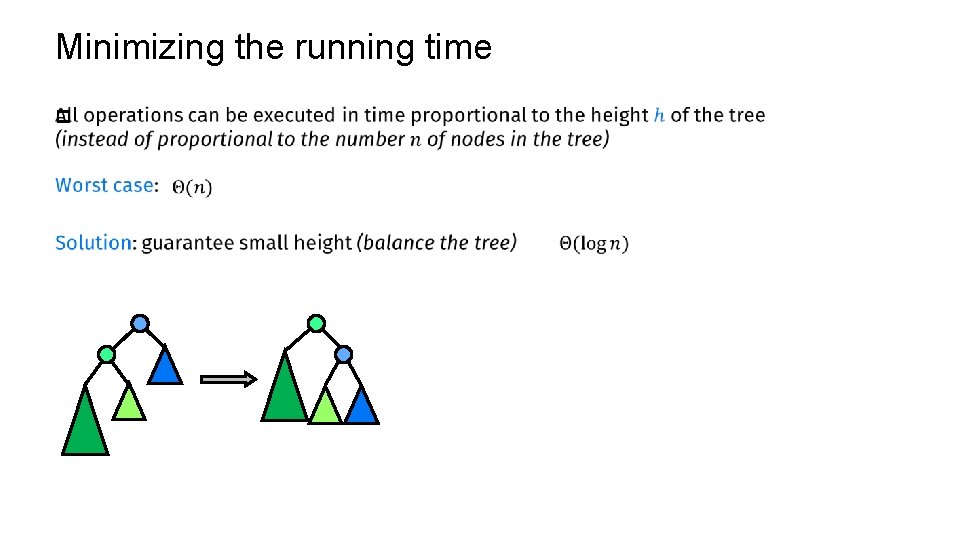
Minimizing the running time p

Balanced binary search trees p

Quiz p

Balanced Search Trees Data Structures & Algorithms

Balanced Search trees There are many methods to balance a search tree. by weight for each node the number of nodes in the left and the right subtree is approximately equal by height for each node the height of the left and the right subtree is approximately equal by degree all leaves have the same depth, but the degree of the nodes differs (hence not a binary search tree)

Weight-balanced search trees p
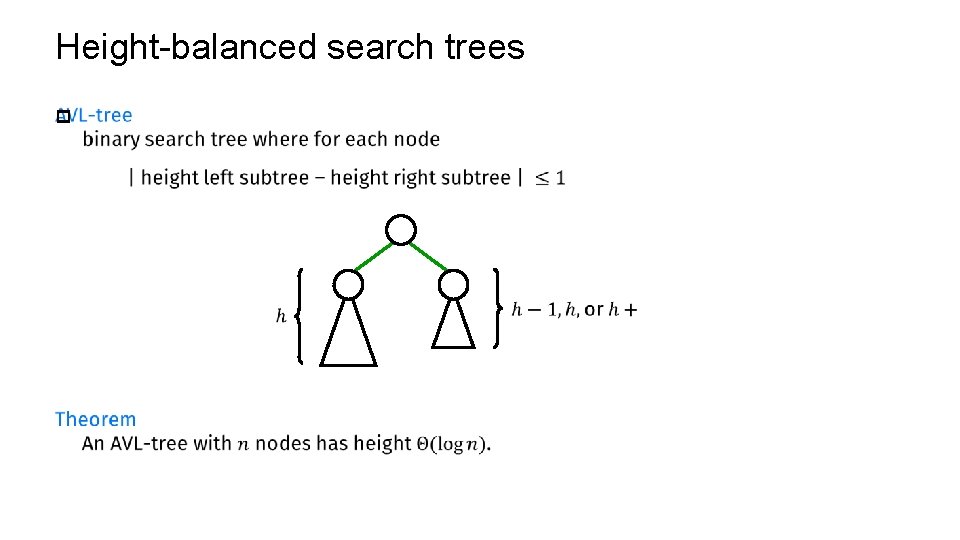
Height-balanced search trees p

Height-balanced search trees p ✔ ✔

Height-balanced search trees p
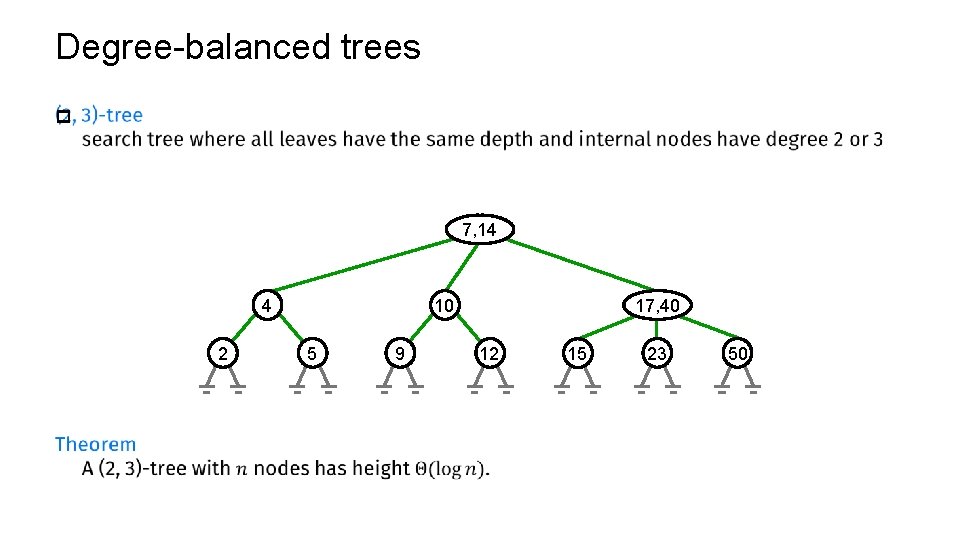
Degree-balanced trees p 7, 14 4 2 10 5 9 17, 40 12 15 23 50

Red-black Trees Data Structures & Algorithms

Data Structure: Binary search trees p
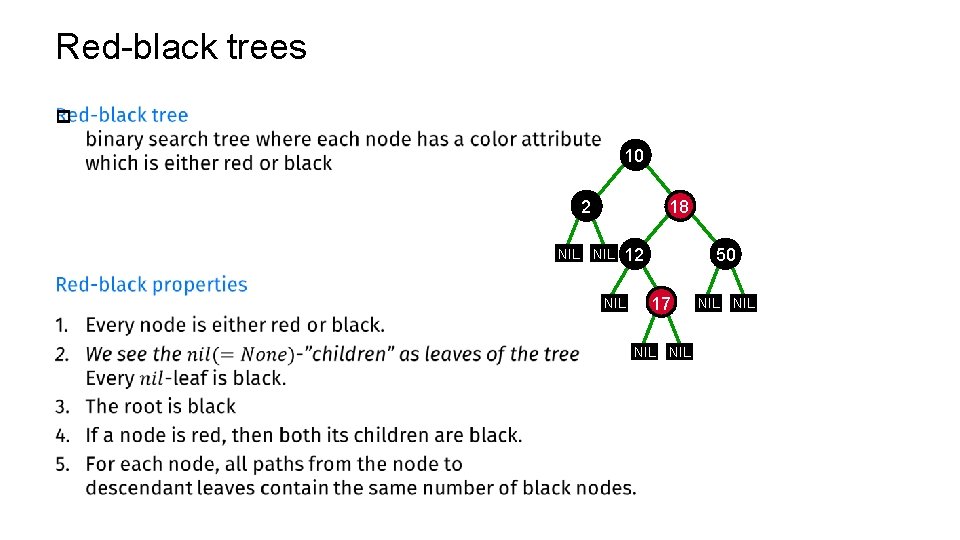
Red-black trees p 10 18 2 NIL 12 NIL 50 17 NIL NIL
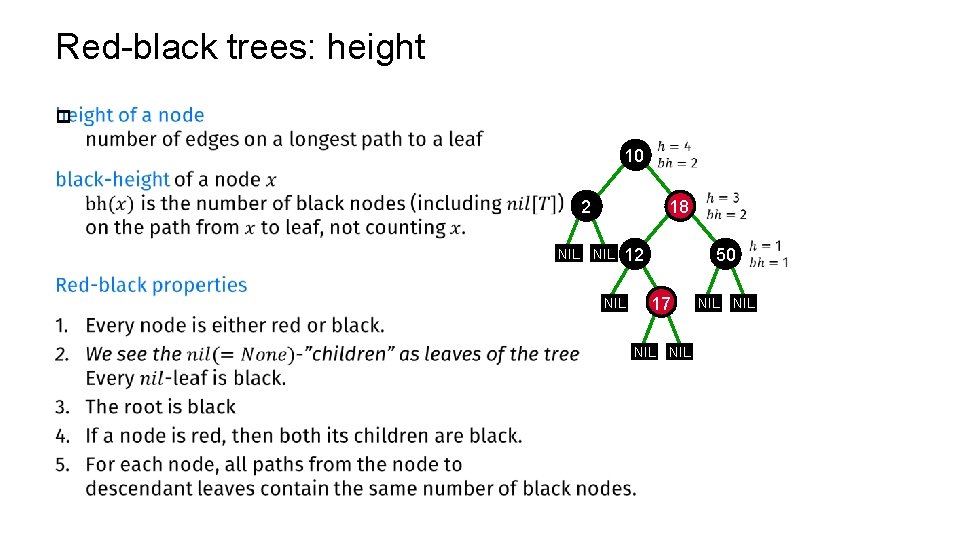
Red-black trees: height p 10 18 2 NIL NIL 12 NIL 50 17 NIL NIL
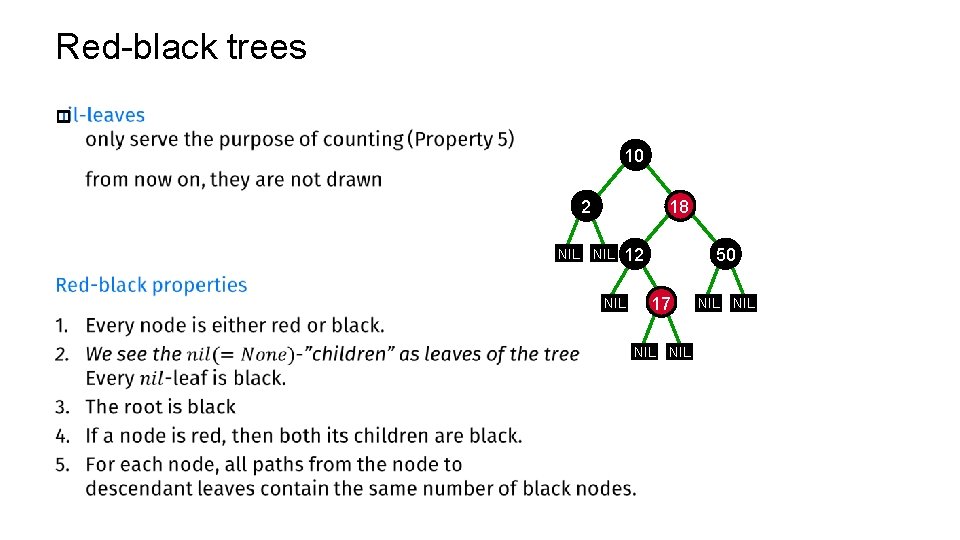
Red-black trees p 10 18 2 NIL NIL 12 NIL 50 17 NIL NIL

Red-black trees p
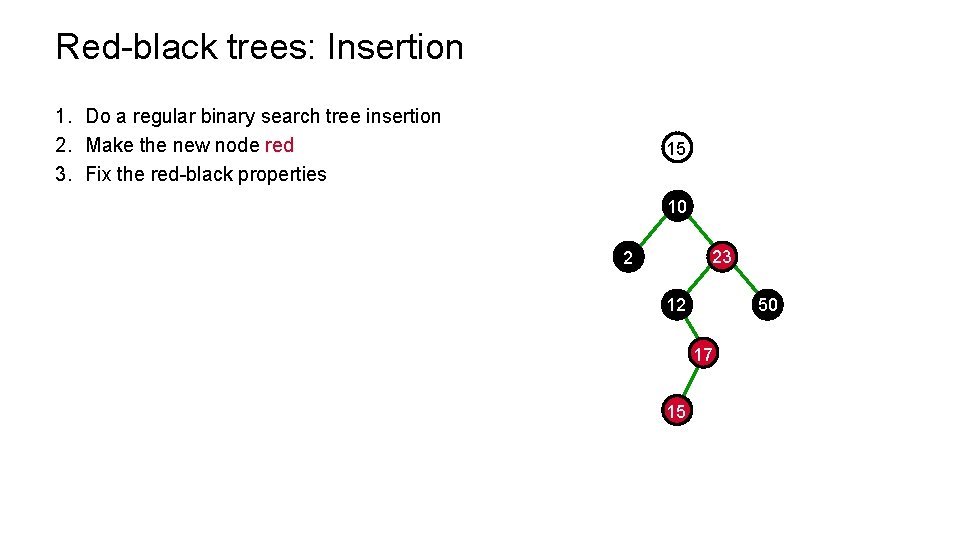
Red-black trees: Insertion 1. Do a regular binary search tree insertion 2. Make the new node red 3. Fix the red-black properties 15 10 23 2 12 50 17 15
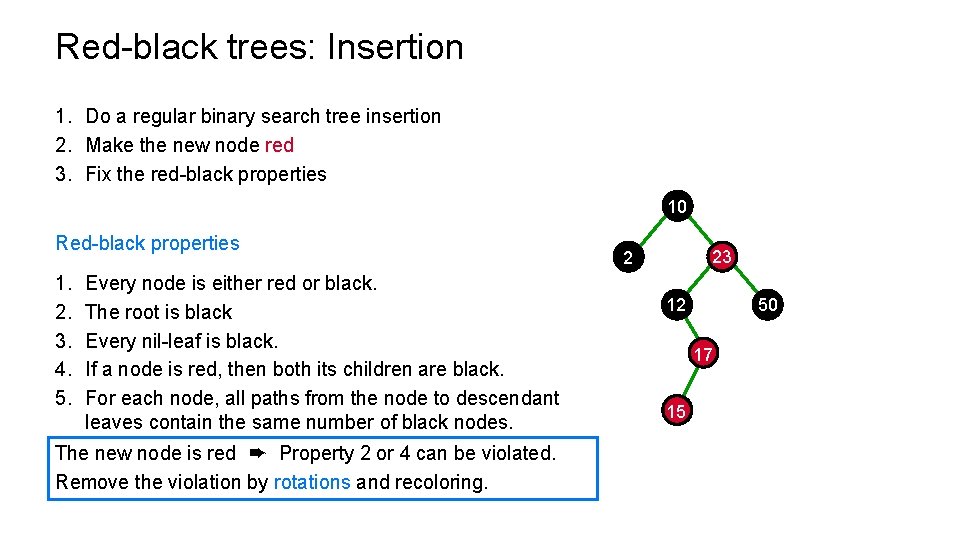
Red-black trees: Insertion 1. Do a regular binary search tree insertion 2. Make the new node red 3. Fix the red-black properties 10 Red-black properties 1. 2. 3. 4. 5. Every node is either red or black. The root is black Every nil-leaf is black. If a node is red, then both its children are black. For each node, all paths from the node to descendant leaves contain the same number of black nodes. The new node is red ➨ Property 2 or 4 can be violated. Remove the violation by rotations and recoloring. 23 2 12 50 17 15
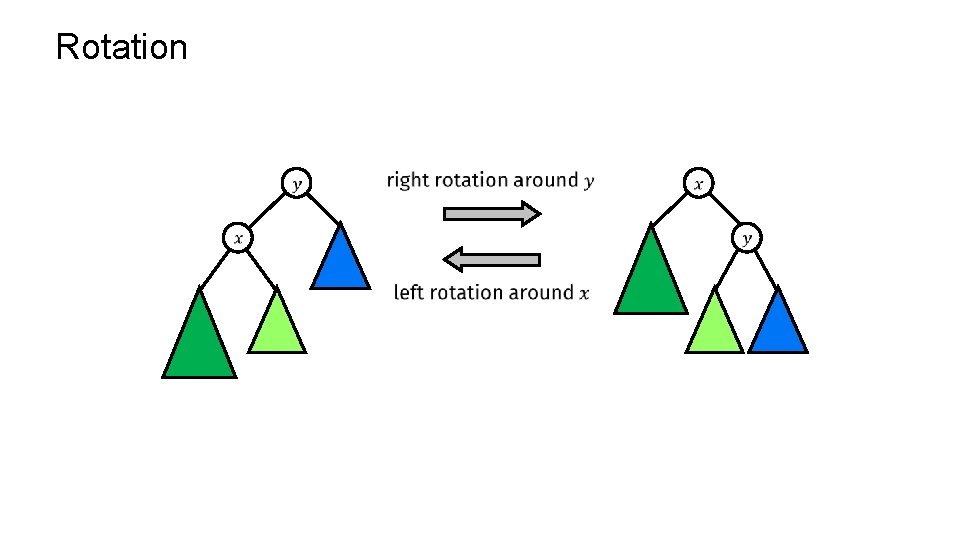
Rotation
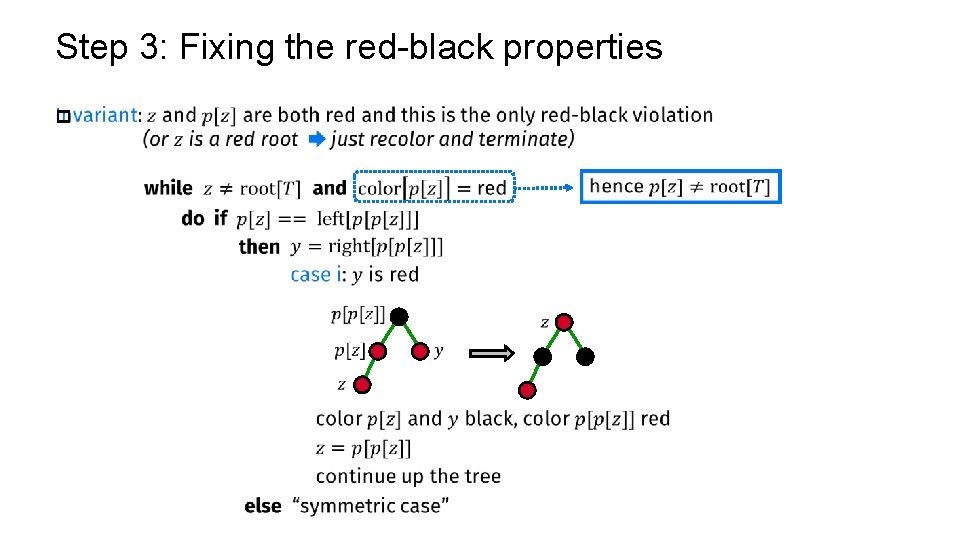
Step 3: Fixing the red-black properties p
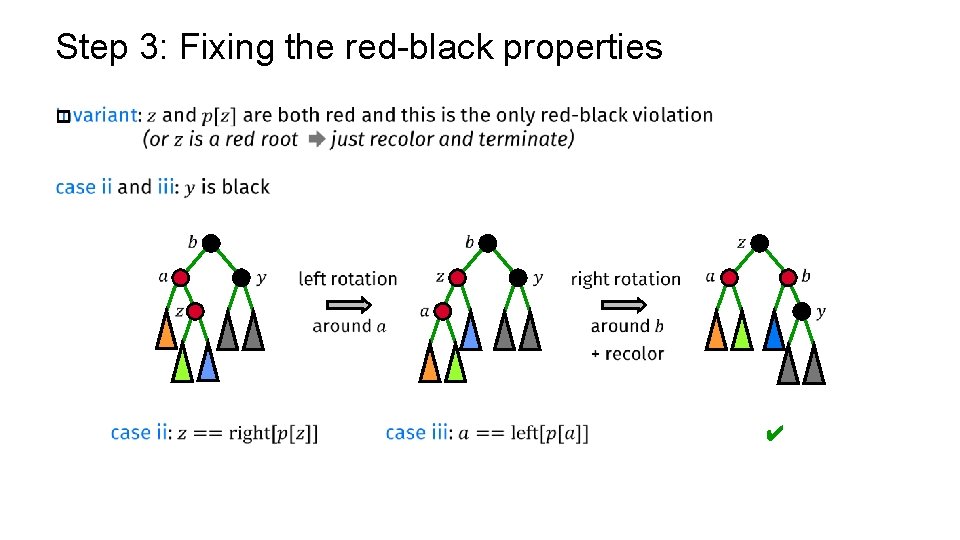
Step 3: Fixing the red-black properties p ✔
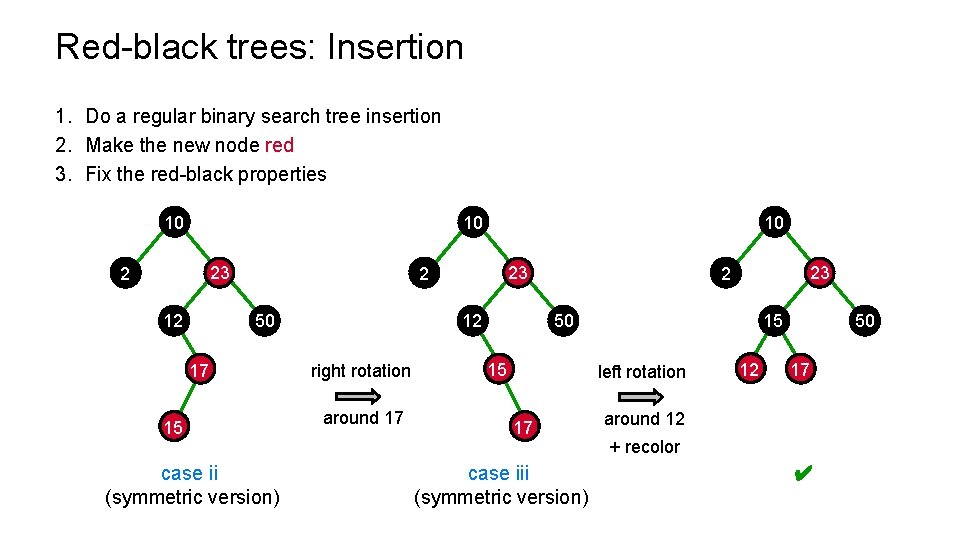
Red-black trees: Insertion 1. Do a regular binary search tree insertion 2. Make the new node red 3. Fix the red-black properties 10 10 23 2 12 10 23 2 50 17 15 case ii (symmetric version) 12 right rotation around 17 23 2 50 15 15 left rotation 17 case iii (symmetric version) 12 50 17 around 12 + recolor ✔

Red-black trees: Insertion p

Red-black trees: Deletion p

Balanced binary search trees p
- Slides: 55