Binary Search and Binary Tree Binary Search Heap

Binary Search and Binary Tree • Binary Search • Heap • Binary Tree

Search on Data • Search is one of fundamentals in computer science • It consists of methods to quickly answer the question, “is there this in the data? ” (called query) One way is to use buckets and hashes • We here approach this problem not from the way of memorizing the data but from the search method

Consult a Dictionary • We will find out the position of a word in the dictionary • How do we do this? + check all words one by one from the beginning called linear scan; O(n) time + open an arbitral page if the word is not there, check the former/latter half faster than linear scan; the candidate pages are refined

Binary Search • For conciseness, we assume that data is a collection of numbers • As preparation, sort the data Let s be the position (index) of 1 st number, and t be that of the last • For query of finding q, we first look at the center if the center is q, answer the position if not, compare q and center to refine the area to be searched t s 1 3 7 8 9 11 13 17 18 19

Refine the Search Area • The center > q q must be in the left side set t to the position just before the center • The center < q q must be in the right side set s to the position just after the center • When t < s, end • Search space is refined to half and half, iteratively t s 1 3 7 8 9 s 11 13 t 17 18 19

Computation time for Binary Search • In each iteration, the search area becomes half or less after at most log 2 n iterations, the search area will be of length one, and the search will terminate computation time is O(log 2 n), that is optimal in the sense of complexity theory • No need of large extra memory, just two variables and the input data of O(n) (called “in place”) • So, very good

Exercise • On the following number sequence, perform a binary search for queries of finding 8, 17 and 19 (trace the movements of s and t ) 1 3 7 8 9 11 13 17 18 19

Weak Points of Array Data • Array needs long time (O(n) time) to keep the increasing order for insertion and deletion at a random position • If we use a list instead of arrays, we can insert/delete in O(1) time, but needs long time (O(n) time) to find the center of the order • In general, it is not trivial to attain efficiency for both search and insertion/deletion • … however, there are some ways

Finding the minimum • We begin with, fast insertion/deletion, and fast search for minimum value, as a first step Problem: + store several (many) numeric values + insertion of new value, and deletion of a value in the data structure has to be done quickly + the minimum value among the values in the data can be found quickly • Generally, a data structure having these functions are called heap

Determine the Winner • Determine the fastest runner in a school • They can not run at once, thus each class determine its fastest; then, we can find the fastest among the class-fastest • The class-fastest is also determined by classifying the students in smaller groups • For determining the strongest football team, two teams can play at once, thus we have a knockout system

Finding the Minimum • Let’s have the same for numeric values (knockout system) • … after the determination, the minimum would be changed when we modify a value; how can we update? • ”A non-minimum value gets smaller” is easy; just compare the value and the minimum. It means that we have to keep only the minimum, for this • When the minimum value increases (or we delete it), we may have to re-compute everything?

Re-computation is NOT Whole • Where do we have to re-compute, when a minimum increases (and becomes non-minimum? ) actually, it is not all • The results above the modified value can change, and others never • In the opposite view, the result which has the modified value below has to be checked

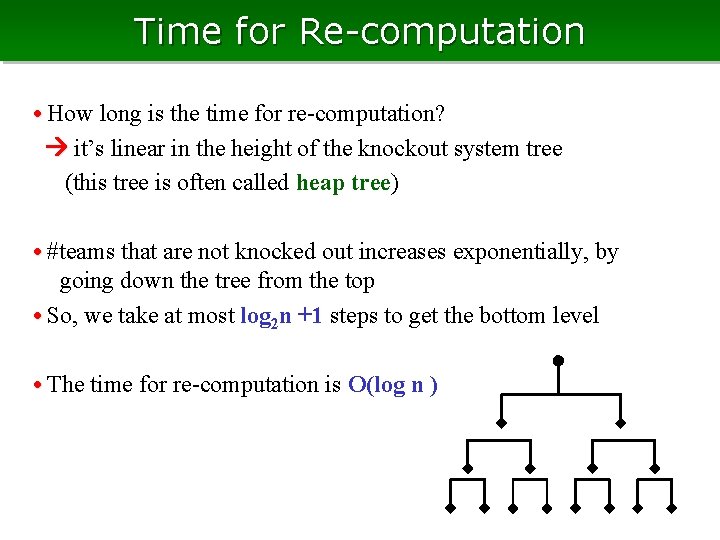
Time for Re-computation • How long is the time for re-computation? it’s linear in the height of the knockout system tree 　　(this tree is often called heap tree) • #teams that are not knocked out increases exponentially, by going down the tree from the top • So, we take at most log 2 n +1 steps to get the bottom level • The time for re-computation is O(log n )

Insertion and Deletion • We keep that the left branch is always no less than the right, everywhere in the tree • To insert a new value to the heap, we put it at the right most position of the bottom level (or, the leftmost of new level if there is no space) • To delete a value, assign the value of the rightmost of the bottom level to the position to be deleted, and reduce the size by one • Both needs O(log n) time

Realize Heap • To realize the heap, we may need something to structure shall we use cell & pointers as list? • Actually, this is a good way Representing the adjacency relation by the pointers, to up, right child, and left child • However, actually, we can do this without pointers

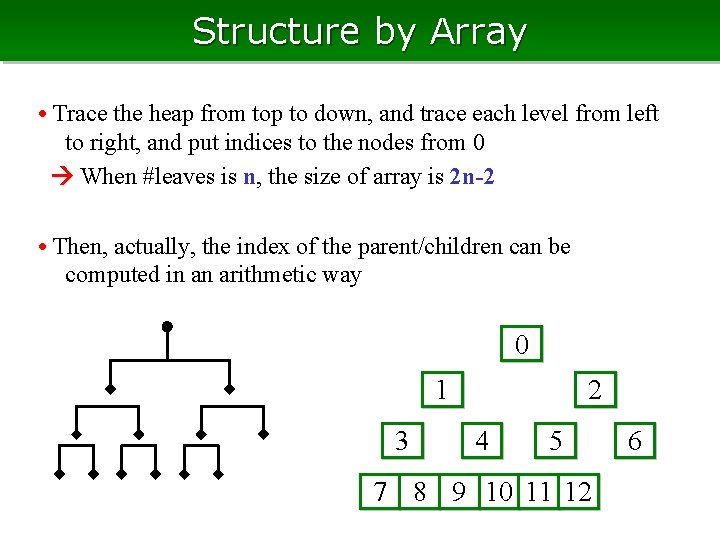
Structure by Array • Trace the heap from top to down, and trace each level from left to right, and put indices to the nodes from 0 When #leaves is n, the size of array is 2 n-2 • Then, actually, the index of the parent/children can be computed in an arithmetic way 0 2 1 3 4 5 7 8 9 10 11 12 6

The Index of Adjacent Cell • The index of the cell adjacent to cell i 　　up (parent)　　　　　 　 　(i-1)/2 (flooring) 　　left-down (left child)　 　　 i*2+1 　　right-down (righ child) 　　 i*2+2 • if i > n-1, then no child 0 2 1 3 4 5 7 8 9 10 11 12 6

Structure of Heap • Heap structure is composed of array, array size, and heap size • A subroutine changes the value of cell i to a typedef struct { void AHEAP_chg ( AHEAP *H, int i, int a ){ int *h; // array for values int j; int end; // size of array H->h[i] = a; int num; // current size of heap while ( i>0 ){ } AHEAP; j = i - 1 + (i%2)*2; // j : = sibling of i if ( H->h[j] < a ) a = H->h[j]; i = (i-1) / 2; // i : = parent of i if ( H->h[i] == a ) break; // no need to update H->h[i] = a; } }

Insert & Delete • To insert, increase num and change the value of the last cell to a void AHEAP_ins ( AHEAP *H, int a ){ H->num++; H->h[H->num*2 -3] = H->h[(H->num*2 -2)/2] AHEAP_chg ( H, H->num*2 -2, a); } void AHEAP_del ( AHEAP *H, int i ){ AHEAP_chg ( H, i, H->h[H->num*2 -2]); AHEAP_chg ( H, (H->num*2 -2)/2, H->h[H->num*2 -3]); H->num--; } 1 3 1 7 1 4 7 9 2 1 8 4 3

Find the Cell of the Minimum Value • 一start from the top cell, and （セル i ）からスタートして、最小値 を持つ子どもの方に降りていく int AHEAP_findmin ( AHEAP *H, int i ){ if ( H->num <= 0 ) return (-1); while ( i < H->num-1 ){ if ( H->h[i*2+1] == H->h[i] ) i = i*2+1; else i = i*2+2; } return ( i ); } 1 3 1 7 1 4 7 9 2 1 8 4 3

Find all ≤ Threshold • Find the left most one ≤ threshold int AHEAP_findlow_leftmost (AHEAP *H, int a , int i){ if ( H->num <= 0 ) return (-1); if ( H->h[0] > a ) return (-1); while ( i < H->num-1 ){ if ( H->h[i*2+1] <= a ) i = i*2+1; else i = i*2+2; } return ( i ); } • Find the one right to cell i ≤ threshold int AHEAP_findlow_nxt (AHEAP *H, int i){ for ( ; i>0 ; i=(i-1)/2 ){ if ( i%2 == 1 && H->h[i+1] <= a ) 1 return (AHEAP_findlow_leftmost (H, a, i+1)); } 7 return (-1); } 1 3 1 4 7 9 2 1 8 4 3

Example of Usage • Sort the numbers (in increasing order) 　+ insert all numbers to a heap 　+ extract the minimum number repeatedly • Clustering on similarity graph (gather nearest pairs, iteratively) 0 2 1 3 4 5 7 8 9 10 11 12 6

Ex. Huffman Tree • We have n words, or something, and each has frequency + insert all frequencies to a heap + extract two minimums, and merge them with the frequency of their sum (they are two children and merged one is their parent) + insert the new one to the heap • Finally, we obtain a tree structure • Assigning 0 to left, 1 to right child, each word gets a 01 code, obtained by tracing the path from the root to it • This code gives an optimal code assignment 35 15 20 11 7 A 9 B 6 C 5 D 4 E 3 F 8

Exercise: Heap • Construct a heap with the following values, and insert the values of 7, 2, and 13, iteratively 4, 6, 8, 9, 11, 15, 17

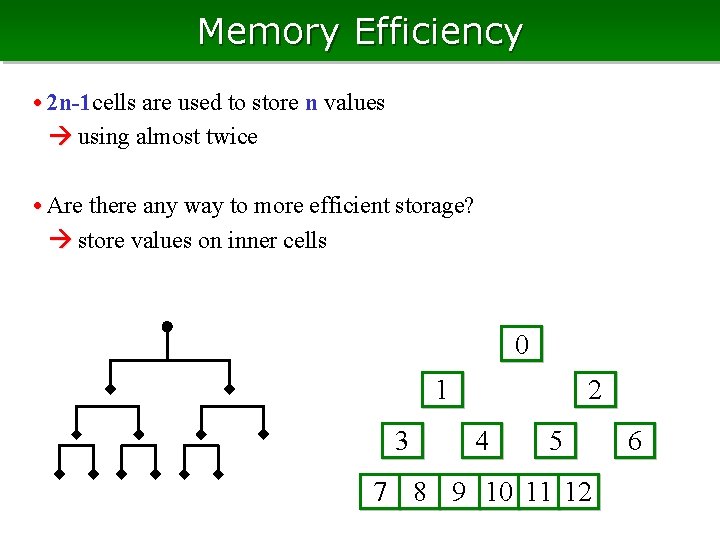
Memory Efficiency • 2 n-1 cells are used to store n values 　 using almost twice • Are there any way to more efficient storage? 　 store values on inner cells 0 2 1 3 4 5 7 8 9 10 11 12 6

Heap on Textbooks • Heap in usual texts is this type • In the “usual heap”, we keep the condition “parent has value smaller than its children” top cell always has the minimum value • We update the heap with keeping this condition, so minimum is easy to find 0 2 1 3 4 5 7 8 9 10 11 12 6

Update Heap + Modification of the value is done by swapping the parent and child in the opposite relation, and go up (down) until the condition will be satisfied + Insertion is done by appending a cell at the right end + Deletion is done by moving the right end cell to there, and decrement the size • Almost the same as the previous one 0 2 7 9 8 3 10 11 9 10 4 4 7

A Code for Value Change • Heap structure is the same • Modify the value of cell i to a void HEAP_chg ( AHEAP *H, int i, int a ){ int aa = H->h[i]; H->h[i] = a; if ( aa > a ) HEAP_chg_up ( H, i ); if ( aa < a ) HEAP_chg_down ( H, i ); } typedef struct { int *h; // array for values int end; // size of array int num; // current size of heap } HEAP;

Update Heap (upward) • Go upward with updating for decreasing the value, and go downward otherwise void HEAP_up ( AHEAP *H, int i ){ int a; while ( i>0 ){ if ( H->h[(i-1)/2]<= H->h[i] ) break; a = H->h[(i-1)/2]; H->h[(i-1)/2] = H->h[i]; H->h[i] = a; i = (i-1)/2 } } typedef struct { int *h; // array for values int end; // size of array int num; // current size of heap } HEAP; • The position of a value changes, thus is disadvantage if we want to store the position of a value

Update Heap (downward) • Increasing a value may result reversal on the parent child constraint • Then, we have to swap parent and child, but we choose the smaller one, and we go down further void HEAP_down ( AHEAP *H, int i ){ int ii, a; while ( i<H->num/2 ){ ii = i*2+1; if (i*2+1 < H->num && H->h[ii]>H->h[ii+1]) ii = ii+1; if ( H->h[ii] >= H->h[i] ) break; typedef struct { a = H->h[ii]; int *h; // array for values H->h[ii] = H->h[i]; H->h[i] = a; int end; // size of array i = ii; int num; // current size of heap } } HEAP; }

Find Values ≤ Threshold • Relatively simple by using recursion int HEAP_findlow ( AHEAP *H, int a , int i ){ if ( i>=H->num ) return; if ( H->h[i] > a ) return; printf (“%dn”, H->h[i] HEAP_findlow ( H, a, i*2+1) HEAP_findlow ( H, a, i*2+2) } 0 2 7 9 8 3 10 11 9 10 4 4 7

Exercise: Heap (2) • Construct a usual heap with the following numbers, and insert numbers 7, 2, and 13, iteratively 4, 6, 8, 9, 11, 15, 17

Column: Speed of Heap in Practice • A heap needs O(log n) time for one operation • However, in practice, it takes 4 or 5 times more compared to usual arrays, even it has 1, 000 cells (log 2 1, 000 ≒ 20 ) • Why does it happen?

Column: Speed of Heap in Practice (2) • A heap update involves operation from the root to a leaf • Once it is done, the cells accessed are stored in cache memory, and can be quickly accessed in the next time • Do this several times, then the upper part of the heap is inside the cache; only lower part needs long memory access time • The phenomenon implies that the lower part is composed of 4 or 5 levels

Here, Terminology on Trees • (In graph theory) the structure composed of vertices (or node) and edges connecting two vertices is called a graph • A graph without a ring (circle, cycle) is called a tree • A tree specified a top vertex called root is called a 根rooted tree • For a vertex x of a rooted tree 　+ vertices on the path between x and the root are ancestors of x 　+ vertices one of whose ancestors is x are descendants of x 　+ the vertex adjacent to x and is an ancestor is the parent of x 　+ the other vertices adjacent to x are children of x 　+ the tree composed of all descendants of x is the subtree rooted at x • A vertex having no child is a leaf • A vertex having some children is an inner vertex • Distance to the root is the depth of a vertex • The max. depth among all vertices is height (depth) • A tree is a binary tree if for any vertex, #children ≤ 2 • A tree is a full binary tree if #children = 0 or 2

Find any Value • Heap is simple, so is good, but we want to find any value from the data in short time • To perform binary search, tree structure like heaps is good, but insertion/deletion take long time under keeping the increasing order • To keep the ordering, we have to be able to delete/insert any position quickly 3 0 2 1 4 5 7 8 9 10 11 12 6

When Order is kept • If the value at the leaves are sorted, we can perform a binary search by going down the tree from the top • To realize this, we write to each node the maximum value among its descendants able to determine left or right, by looking at this value • This is realized with quick insertion/deletion, by allowing ill-formed tree + we attach two children to the vertex having the value just larger than the inserting value + copy the sibling vertex to the parent, and delete the both children

Skew would Grow • Search/update time is linear in the depth of the target leaf • They are fast when the tree is balanced so that the height of the tree is low, but take long time when the tree is skewed happens by many insertion at the same place • To fasten the operation, we need to derive something

Eliminate the Skew • Optimal search time is O(log n ) • So, try to bound the time by c log n for some constant c • When deep leaves exist, shallow places must be somewhere else deepen the shallow area and make deep places shallow, with keeping the ordering • This could be done by re-formulation of trees locally, by rotating the children and their parents

Balancing by Rotation • Suppose that there are consecutive two vertices such that the left is two more higher than the right • We swapping the positions of the parent and the child (rotation) • By a rotation, gap of the heights decreases by two ≥ 2

Bounding the Height • For any vertex, the heights of children do not differ two, by repeatedly applying the rotation • Can we say something about the height k? + there is at least one vertex of depth k-1 　　(in another branch, branched at the root, or the child of the root) + At least two vertices of k-2 　　(branched at the depth of 2 or 3) + At least 2 h-1 vertices of depth k-h 　　(branched at 2 h or 2 h+1) …. The number of vertices in the tree is at least 2 k/3 • If there are n leaves, ら、高さは 3 log 2 n ＝ O(log n) Such a tree of height O(log n) is called a balanced tree

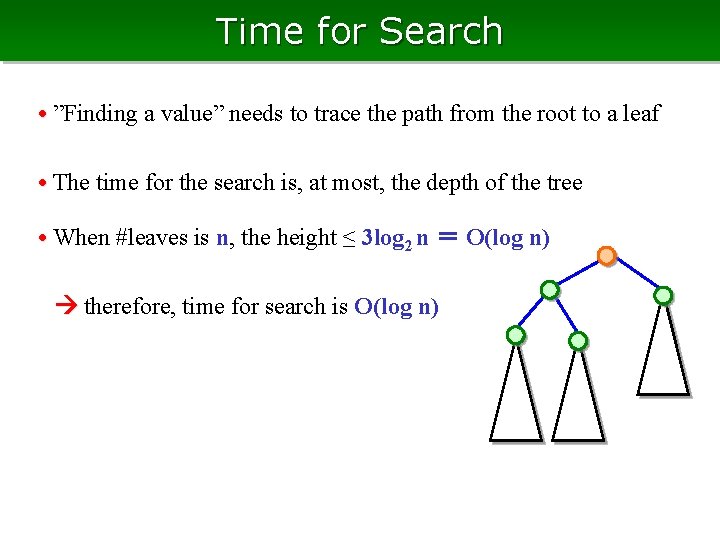
Time for Search • ”Finding a value” needs to trace the path from the root to a leaf • The time for the search is, at most, the depth of the tree • When #leaves is n, the height ≤ 3 log 2 n ＝ O(log n) 　 therefore, time for search is O(log n)

Effects by Rotation • When we rotate the tree at vertex x, are there any new vertex such that we now have to rotate the vertex? 　+ descendants of x: OK, the heights of their children do not change 　+ non-ancestor & non-descendants of x is also OK 　+ For ancestors x, the height of one child can change • … so, if we rotate at a vertex, its ancestors may have to be rotated We thus rotate from the vertex to the root, iteratively

Insertion and Deletion • We insert or delete a vertex, then its ancestors may violate the condition to be balanced • The height increase/decreases by one, thus one rotation is sufficient to each ancestor • Trace the ancestors from the vertex operated, and perform rotation if necessary (can stop if rotation is not needed at an ancestor) • The height of tree is O(log n), and a rotation can be done in a constant time, thus insertion and deletion with re-balancing can be done in O(log n) time • This rotation does not affect to any its ancestor (the number of descendants is not changed by rotation)

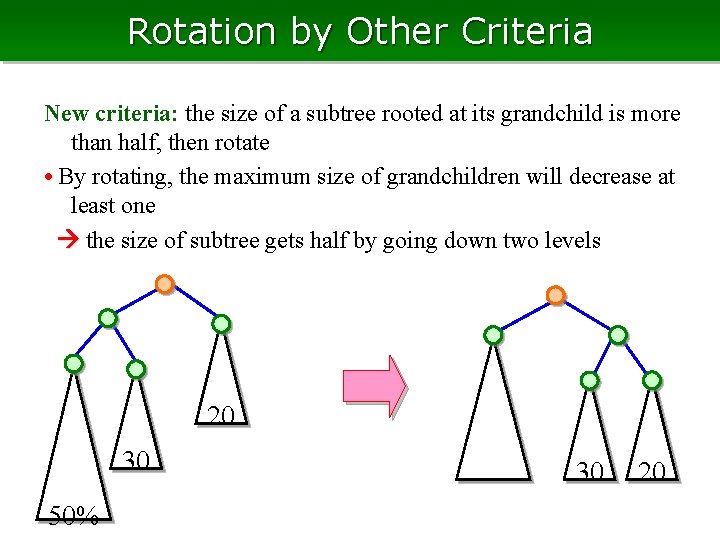
Rotation by Other Criteria New criteria: the size of a subtree rooted at its grandchild is more than half, then rotate • By rotating, the maximum size of grandchildren will decrease at least one the size of subtree gets half by going down two levels 20 30 50% 30 20

The height of Tree • Get half by two levels, thus we can go down at most 2 log 2 n levels the height is at most 4 log 2 n ＝ O(log n) if #leaves is n 20 30 50%

Insertion and Deletion • This rotation does not affect to any its ancestor (the number of descendants is not changed by rotation) • Trace the ancestors from the vertex operated, and perform rotation if necessary (not stop even if rotation is not needed at an ancestor) • The height of tree is O(log n), and a rotation can be done in a constant time, thus insertion and deletion with re-balancing can be done in O(log n) time

Structure for Binary Tree • We need pointers in this case, since the shape of binary tree is not uniform and periodical • For the rotation threshold, we keep the height and size of the subtree, rooted at each vertex • We can represent the structure by array, as list typedef struct { BTREE *p; // -> parent BTREE *l; // -> left child BTREE *r; // -> rigth child int height; // height of subtree int value; // (max) value } BTREE;

Example of Usages • Dictionary data, storage for IDs • Keyword search in a document …

Exersice: Binary Tree • Rotate the vertices of the following tree, that are necessary (examine two criteria) 　　

Many Children • Each vertex of a binary tree always has two children • Why two? + update cost is optimal + search and update will be the same costs + operation for children becomes simple • Can we get advantage by allowing more than two children? • 2 -3 tree is an example; #children is 2 or 3 + the depths of all leaves are the same + however, operations for children are not simple (choosing minimum among three, split three into two, …) • Can we increase the number more?

B-tree • A tree is a B-tree if #children of any vertex is bounded by B • There are some motivations for this • Consider HDD or tape, that take much cost to access a block, but reading a block takes not so long time compared to reading a bit the computation time depends on #blocks we accessed • Then, simple solution is to increase the maximum number of children, that fits a block

Update of B-tree • If the definition is “all vertices have exactly B children”, the memory usage is efficient however, we have to frequently update everywhere • However, the efficiency is less if many vertices have few children bound the number of children from B/2 to B if a parent and its child, or two siblings have at most B children in total, we merge them into one node • By applying rotation, the height of the tree is bounded by O(log. B/2 n) 　　

Summary Binary search: search area is refined half, at most log n times Heap: 　simulate update of knockout system Binary tree: rotate at vertices to re-balance the tree B-tree: 　minimize the blocks to be accessed