Binary Octal and Hexadecimal The number bases used

Binary, Octal and Hexadecimal The number bases used in computers Copyright 2005 Curt Hill

T-Shirt • There are 10 kinds of people: • Those that understand binary • Those who don’t Copyright 2005 Curt Hill

Binary • • • Binary is a base two number system It is widely used because of electronics A switch is a two value device Binary uses two values for each digit Thus computer memory and storage is usually in binary • Before dealing with binary we should review what we already know: decimal Copyright 2005 Curt Hill

Decimal • What are the characteristics of decimal system? • Ten occurs twice: – Number of distinct digits – The power that each place value digit is raised • So what does 8245 mean? Copyright 2005 Curt Hill

Decimal numbers 8245 Ten possible digits 0 -9 All places raised to a power of ten 0 10 5× 1 4 × 10 2 2 × 10 8 × 103 = 5 = 40 = 200 = 8000 Copyright 2005 Curt Hill

Binary is Similar • There are two possible digits 0 and 1 • All places are raised to a power of 2 • The arithmetic fact tables are much smaller • The representation of a number is much bulkier Copyright 2005 Curt Hill

Binary numbers 10110 = 2 = 4 = 0 = 16 Five or six digits of binary is just two of decimal 22 0 2 0× 1 × 21 2 1× 2 0 × 23 1 × 24 Copyright 2005 Curt Hill

Converting binary to decimal 1. Have a variable, call it T, which will contain the powers of two. Initialize it to 1. 2. Have a variable, call it D, which will contain the decimal number. Initialize it to 0. 3. Position yourself to the right-most digit of the binary number. 4. While there are still digits to the left of the current one do steps 5 - 8. 5. If the digit in the current position is 1 6. Then add the value of T to D 7. Double T. 8. Move the current position one digit to the left. Copyright 2005 Curt Hill

More Examples • What is 1010110? • Starting at the right: – 0 + 2 + 4 + 0 + 16 + 0 + 64 = 86 • What is 1110011? • Starting at the right: – 1 + 2 + 0 + 16 + 32 + 64 = 115 • What is 11101010? • Starting at the right: – 0 + 2 + 0 + 8 + 0 + 32 + 64 + 128 = 234 Copyright 2005 Curt Hill

Decimal to Binary • Somewhat uglier but still managable • The process starts with decimal number and subtracts successively smaller power of two from it • If it can be subtracted produce a 1 otherwise a zero Copyright 2005 Curt Hill

Decimal Conversion Example • • Start with 50 The largest power of 2 less than this is 32 (25) The binary number is 1 xxxxx Subtracting 50 – 32 gives 18 Now subtract 16 to get 11 xxxx and 2 No 8 s or 4 s can be subtracted giving 1100 xx Subtract 2 – 2 giving 11001 x and 0 No 1 s can be subtracted giving 110010 Copyright 2005 Curt Hill

Decimal to Binary Again 150 -128 22 -16 6 -4 2 -2 0 Starting number Any 128 s? Yes. Subtract, place a one. Any 64 s? No. Place a zero. Any 32 s? No. Place a zero. Any 16 s? Yes. Subtract, place a one. Any 8 s? No. Place a zero. Any 4 s? Yes. Subtract, place a one. Any 2 s? Any 1 s? No. Place a zero. 1 ___ 0 __ 1 __ 0 __ 128 64 32 16 8 Copyright 2005 Curt Hill 4 2 1

Decimal Conversion Algorithm 1. Have a variable, call it D, which is initialized to the value of the decimal number needing conversion. 2. Have another variable, call it T, that is initialized to the largest power of two that is smaller than D. 3. While D > 0 do steps 4 - 8. 4. If D >= T 5. Then subtract T from D 6. Write a 1 7. Else write a 0 8. Divide T by 2 Copyright 2005 Curt Hill
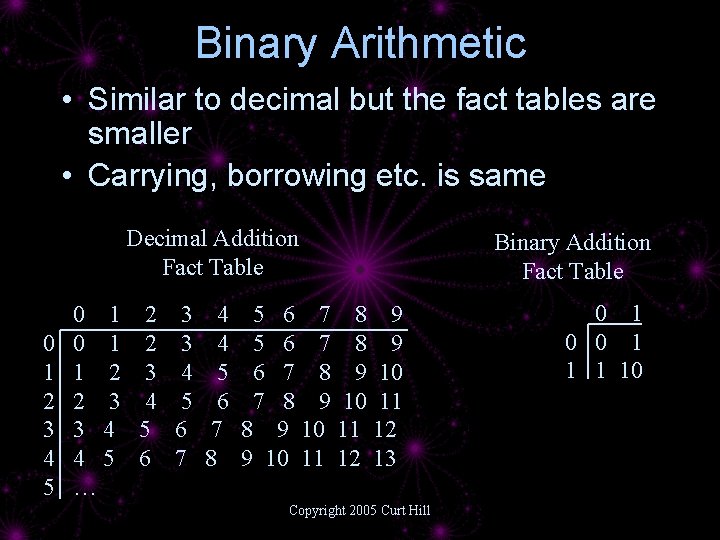
Binary Arithmetic • Similar to decimal but the fact tables are smaller • Carrying, borrowing etc. is same Decimal Addition Fact Table 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 12 13 … Copyright 2005 Curt Hill Binary Addition Fact Table 0 1 0 0 1 10

Binary Addition 1 1 1 0111011 0110010 1 1 01 If we convert to decimal does it sum the same? Copyright 2005 Curt Hill

Other bases • Binary has some problems, the largest of which is that it is very bulky • Decimal from binary is not an easy conversion – It also obscures structure • Most manufacturers use another power of two base to show things – Octal – base 8 = 23 – Hexadecimal – base 16 = 24 Copyright 2005 Curt Hill

Octal • Base 8 has 8 digits, 0 – 7 and every place is raised to a power of 8 • Conversion to and from binary is way too easy – Partition into groups of 3 bits from right to left – Convert the three bits to octal • Preferred by certain manufacturers such as DEC and Intel Copyright 2005 Curt Hill

Binary – Octal Conversion Start with binary 0110111001011101 Partition (right to left) in groups of 3 Write digits 0110111001011101 0 6 7 1 3 How easy is that? Conversion of octal to binary is the reverse Copyright 2005 Curt Hill 5

Hexadecimal • Base 16 has 16 digits, 0 – 9, A-F and every place is raised to a power of 16 – A=10, B=11, C=12, D=13, E=14, F=15 • Conversion to and from binary is also easy – Partition into groups of 4 bits – Convert the four bits to hexadecimal • Preferred by certain manufacturers such as IBM and Burroughs Copyright 2005 Curt Hill

Binary – Hexadecimal Conversion Start with binary 0110111001011101 Partition (right to left) in groups of 4 Write digits 0110111001011101 6 E 5 D How easy is that? Conversion of hexadecimal to binary is the reverse Copyright 2005 Curt Hill
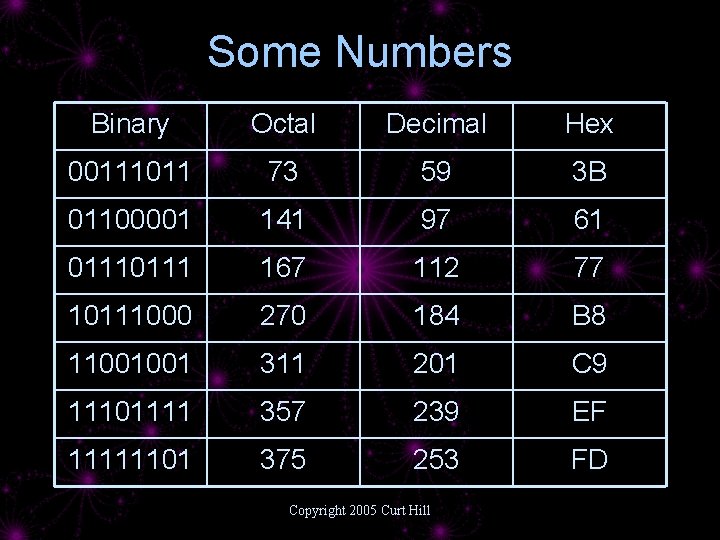
Some Numbers Binary Octal Decimal Hex 00111011 73 59 3 B 01100001 141 97 61 0111 167 112 77 10111000 270 184 B 8 11001001 311 201 C 9 11101111 357 239 EF 11111101 375 253 FD Copyright 2005 Curt Hill
- Slides: 21




































