Binary number system This material from T 529

Binary number system (This material from T 529 ICT CD-ROM) n n n The number system with base 2 (uses two values 0, 1) Our conventional number system, the denary system, uses base 10 (uses ten values 0, 1, 2, 3, . . . 9) The fact that binary digits can have only one of two states makes the binary system very suitable for use in electronic computation, data storage (electronic memory) and communications. In these fields, circuits that can exist in one of only two electrical states (represented by 0 and 1) are simple to design and can be mass produced N bits is suitable to present 2 N denary numbers from 0 to 2 N – 1 w For Example, 8 bits is suitable to present (28 = 256) numbers from 0 to 255 Continue Prepared by: Eng. Ali H. Elaywe 1

Example n Try to find the denary equivalent of 11001101? w (1 × 27) + (1 × 26) + (0 × 25) + (0 × 24) + (1 × 23) + (1 × 22) + (0 × 21) + (1 × 2 0) w = 128 + 64 + 0 + 8 + 4 + 0 +1 w = 128 + 64 + 8 + 4 + 1 w = 205 in denary n The leftmost bit is called the most-significant bit and the rightmost bit is called the least-significant bit Prepared by: Eng. Ali H. Elaywe Continue 2

230 – 128 102 – 64 1 38 – 32 1 6 – 16 1 . . . 6 – 8 0 . . . 6 – 4 0 2 – 2 1 0 – 1 1 . . . 0 Converting from denary to binary n Try to convert 230 denary number to 8 -bit binary number? 27 (128) 26 (64) 25 (32) 24 (16) 23 (8) 22 (4) 21 (2) 20 (1) The binary number can then be read off from top to bottom; it is 1110 0110 Prepared by: Eng. Ali H. Elaywe Continue 3

Hexadecimal system (this material from T 529 ICT CD-ROM) n n n The positional number system using as its base the number 16 The first ten numbers in hexadecimal are represented by the numerals 0, 1, 2, 3, …, 9 exactly as in denary numbers. The next six numbers, equivalent to the denary numbers 10– 15, are represented by A–F The hexadecimal system is often used in computer applications Prepared by: Eng. Ali H. Elaywe Continue 4

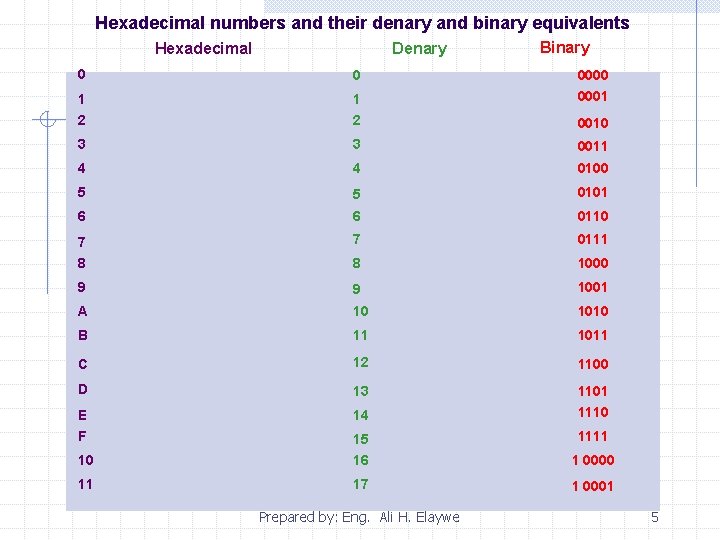
Hexadecimal numbers and their denary and binary equivalents Hexadecimal Denary Binary 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 A 10 1010 B 11 1011 C 12 1100 D 13 1101 E 14 1110 F 15 1111 10 16 1 0000 11 17 1 0001 Prepared by: Eng. Ali H. Elaywe 5

Converting from Hexadecimal to denary n Example w Find the denary equivalent of hexadecimal EB 7 ? n n = (E × 162) + ( B × 161) + (7 × 160) = (14 × 162) + (11 × 161) + (7 × 160) = (14 × 256) + (11 × 16) + (7 × 1) = 3767 Prepared by: Eng. Ali H. Elaywe Continue 6

hexadecimal and binary conversion (very easy) n n Hexadecimal notation provides a compact way of representing large binary numbers, as each group of four binary digits can be represented by a single hexadecimal number Example 1: converting from binary to hexadecimal w Try to represent the binary number 10111110 as a hexadecimal number, first group the number into 4 -bit groups as following: 1011 1110 w Now convert each 4 -bit binary number to its hexadecimal equivalent: So 1011 1110 is equivalent to BE n If the binary number is not divisible into four-digit groups (for example, if it has 7 bits), leading zeros are added to make the number of bits into a multiple of four Prepared by: Eng. Ali H. Elaywe Continue 7

n Example 2: converting from hexadecimal to binary w Try to represent the Hexadecimal number AF 7 as a binary number? n 1) Find binary representation (4 -bit) of each hexadecimal number separately: n n n A is equal to 10 = 1010 F is equal to 15 = 1111 7 is equal to 7 = 0111 2) Put these binary representation in correct order: A F 7 1010 1111 0111 So the result is: 1010111 Prepared by: Eng. Ali H. Elaywe Continue 8

Activity 1. 5 (self-assessment / revision) (a) What is meant by (i) Error detection is a process whereby pieces of binary data are checked while they are being manipulated or transmitted, in order to discover whether an error has occurred, If an error is detected, a special action usually follows: for example a request for retransmission of the binary data, or the display of an error message (ii) Error correction: If an error is detected (in erorr detection), it is corrected Error detection and correction used both for computer systems (e. g. data storage) and digital communication systems (transmission and reception of digital data) Prepared by: Eng. Ali H. Elaywe Continue 9

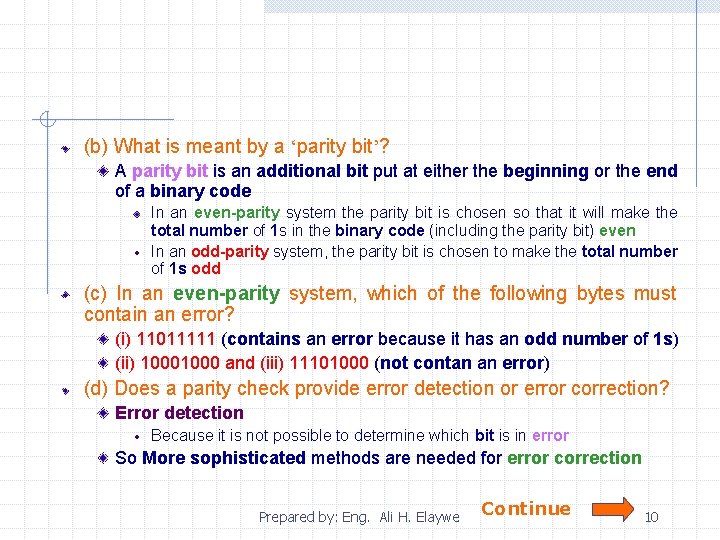
(b) What is meant by a ‘parity bit’? A parity bit is an additional bit put at either the beginning or the end of a binary code In an even-parity system the parity bit is chosen so that it will make the total number of 1 s in the binary code (including the parity bit) even In an odd-parity system, the parity bit is chosen to make the total number of 1 s odd (c) In an even-parity system, which of the following bytes must contain an error? (i) 11011111 (contains an error because it has an odd number of 1 s) (ii) 1000 and (iii) 11101000 (not contan an error) (d) Does a parity check provide error detection or error correction? Error detection Because it is not possible to determine which bit is in error So More sophisticated methods are needed for error correction Prepared by: Eng. Ali H. Elaywe Continue 10

Hamming code (this material from T 529 ICT CD-ROM) • • It is a simple technique for error correction The Hamming code uses redundant bits in such a way that when an error occurs the redundant bits indicate where it has occurred Here we are suppose that we have 4 -bit code (A, B, C, D The trick is to add three redundant bits, called X, Y and Z, to each 4 -bit pattern ABCD in such a way that if an error occurs in any one of the resulting seven bits the receiver can calculate where the error must have been. The receiver can therefore correct the error without any more help from the transmitter Prepared by: Eng. Ali H. Elaywe Continue 11

A- The Job of the sender: Suppose that the message to be sent is the number 2 (0010 in binary). Then A is 0, B is 0, C is 1 and D is 0 The four bits ABCD are taken in groups of three, BCD, ACD and ABD and an even parity check bit is calculated for each group Let X represent the parity check bit for BCD, Y the parity check bit for ACD and Z the parity check bit for ABD. The group BCD is 010 so the even parity bit X will be 1, because that makes the number of 1 s even Group ACD is 010, so Y will be 1 Group ABD is 000, so Z will be 0 So Bits X, Y and Z are now attached to the original code ABCD to form a seven-bit code word ABCDXYZ. In the example, the word is 0010110 and this is the code word transmitted Prepared by: Eng. Ali H. Elaywe Continue 12

B- The Job of the reciever When seven-bit code arrives, is to carry out even-parity checks on the groups BCDX, ACDY and ABDZ. The receiver checks whether each of the groups BCDX, ACDY and ABDZ has an even number of 1 s. If none of the groups fail this parity check, then no error has occurred in transmission and the redundant bits can be ignored If all three parity checks fail, the source of the error must be bit D, since only bit D appears in all three parity-check groups The table 2 below show the eight possible situations of the evenparity checks on BCDX, ACDY and ABDZ. If a check fails it is recorded as a 1 in the appropriate column, and if it succeeds it is recorded as a 0. Thus the first row (0, 0, 0) indicates that even parity was found on all three checks The bottom row indicates that all three even-parity checks failed Prepared by: Eng. Ali H. Elaywe Continue 13

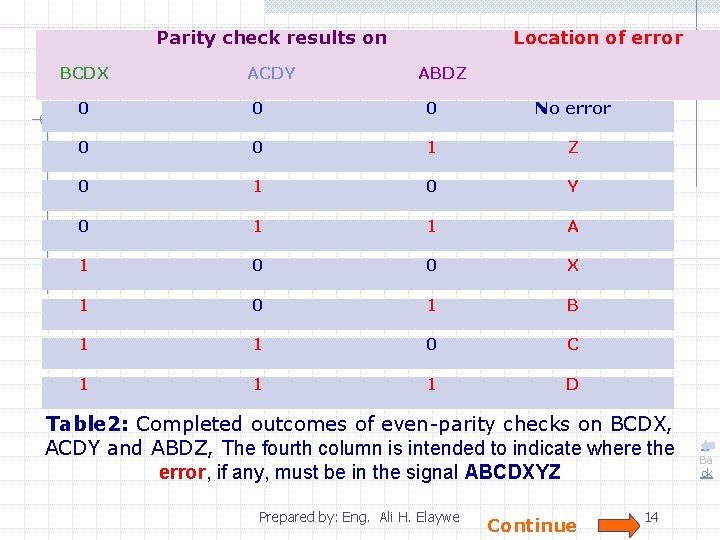
Parity check results on BCDX ACDY Location of error ABDZ 0 0 0 No error 0 0 1 Z 0 1 0 Y 0 1 1 A 1 0 0 X 1 0 1 B 1 1 0 C 1 1 1 D Table 2: Completed outcomes of even-parity checks on BCDX, ACDY and ABDZ, The fourth column is intended to indicate where the error, if any, must be in the signal ABCDXYZ Prepared by: Eng. Ali H. Elaywe Continue 14 Ba ck

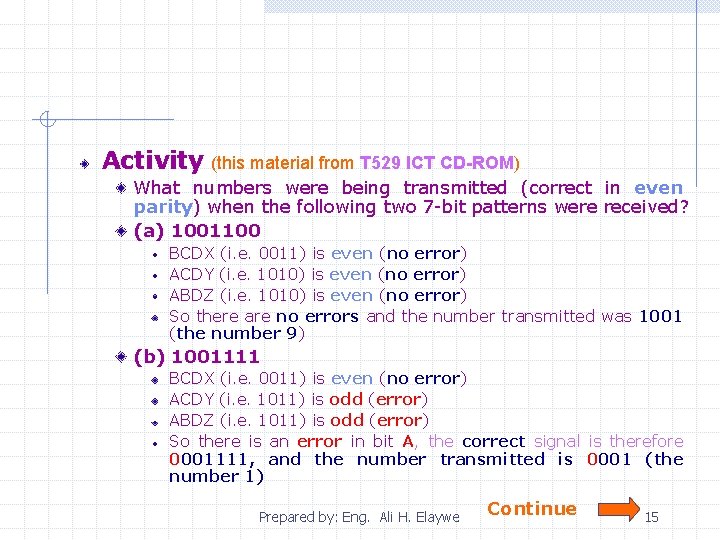
Activity (this material from T 529 ICT CD-ROM) What numbers were being transmitted (correct in even parity) when the following two 7 -bit patterns were received? (a) 1001100 BCDX (i. e. 0011) is even (no error) ACDY (i. e. 1010) is even (no error) ABDZ (i. e. 1010) is even (no error) So there are no errors and the number transmitted was 1001 (the number 9) (b) 1001111 BCDX (i. e. 0011) is even (no error) ACDY (i. e. 1011) is odd (error) ABDZ (i. e. 1011) is odd (error) So there is an error in bit A, the correct signal is therefore 0001111, and the number transmitted is 0001 (the number 1) Prepared by: Eng. Ali H. Elaywe Continue 15

Topic 6: Preparation for Next Session 1) Read Part 1 of Book T 2) Do all activities in Part 1 of Book T including links to Book C and Book D 3) Complete the Journal items related to Part 1 of Book T 4) Do activity 1. 18 (Journal) 5) Skim Part 2 of Book T Prepared by: Eng. Ali H. Elaywe 16