Binary Negatives Addition Subtraction Storing Negative Integers Another

Binary Negatives, Addition, Subtraction

Storing Negative Integers • Another method is 2 s Complement n -75 128 64 32 16 -128 1 0 1 1 8 4 2 1 0 1 n-128+32+16+4+1=-75

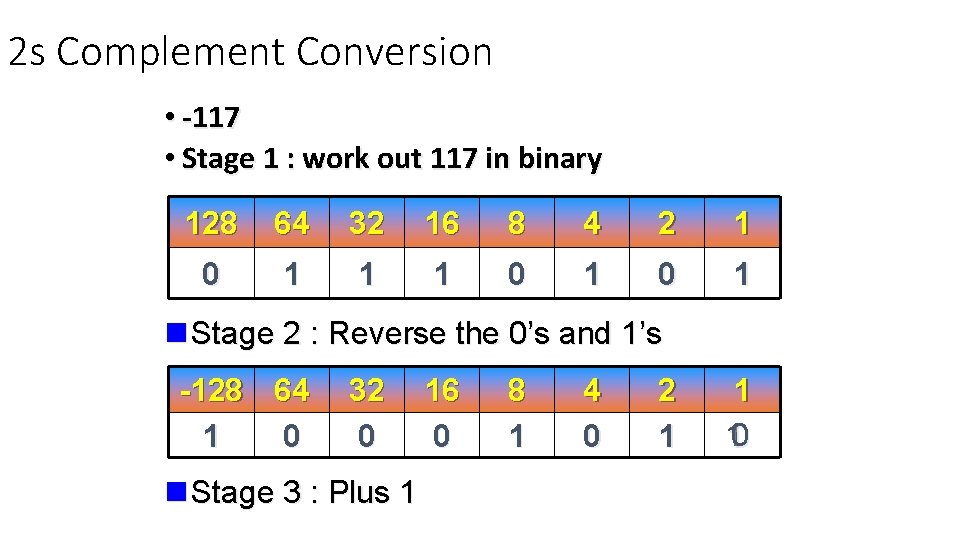
2 s Complement Conversion • -117 • Stage 1 : work out 117 in binary 128 64 32 16 8 4 2 1 0 1 1 1 0 1 n Stage 2 : Reverse the 0’s and 1’s -128 64 1 0 32 0 n Stage 3 : Plus 1 16 0 8 1 4 0 2 1 1 10

Binary Addition • In binary these are the possible sums… • • • 0+0=0 0+1=1 1+0=1 1 + 1 = 0, carry 1 1 + 1 = 1, carry 1 1 + 1 + 1 = 0, carry 1

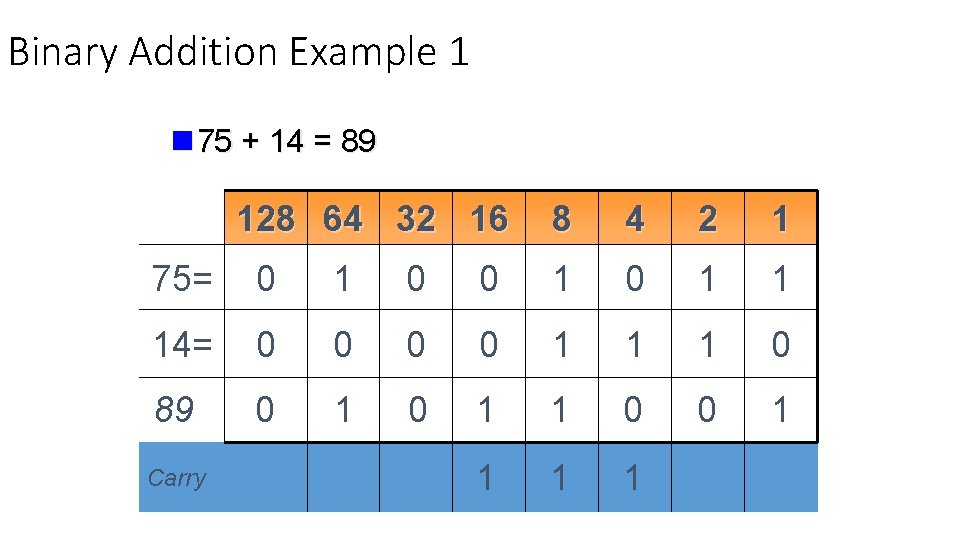
Binary Addition Example 1 n 75 + 14 = 89 128 64 32 16 8 4 2 1 75= 0 1 0 1 1 14= 0 0 1 1 1 0 89 0 1 1 0 0 1 1 Carry

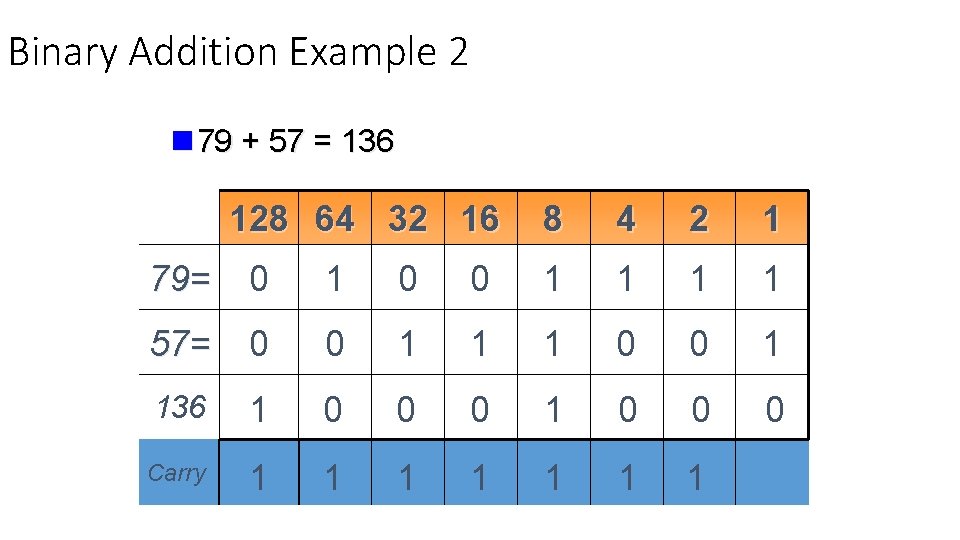
Binary Addition Example 2 n 79 + 57 = 136 128 64 32 16 8 4 2 1 79= 0 1 0 0 1 1 57= 0 0 1 1 1 0 0 1 136 1 0 0 0 Carry 1 1 1 1

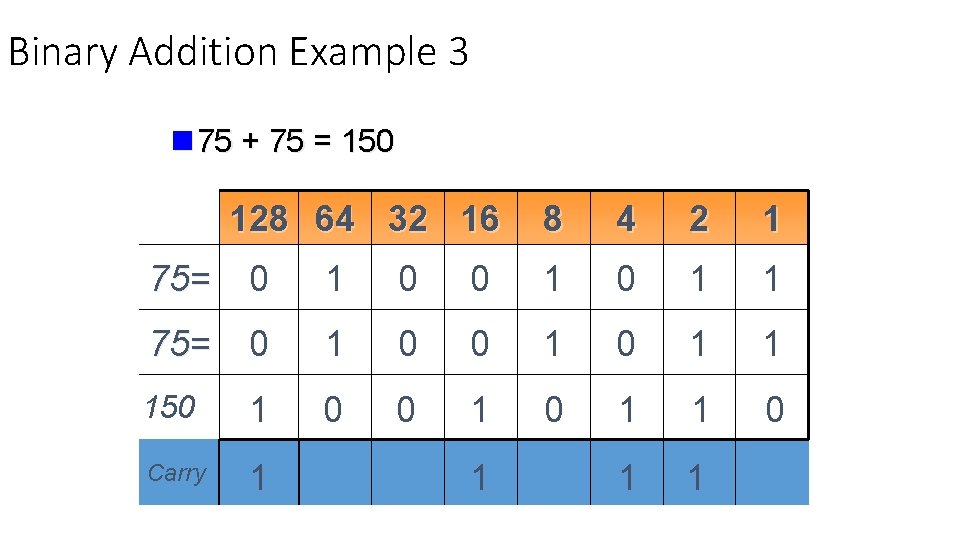
Binary Addition Example 3 n 75 + 75 = 150 128 64 32 16 8 4 2 1 75= 0 1 0 1 1 150 1 0 1 1 0 Carry 1 1

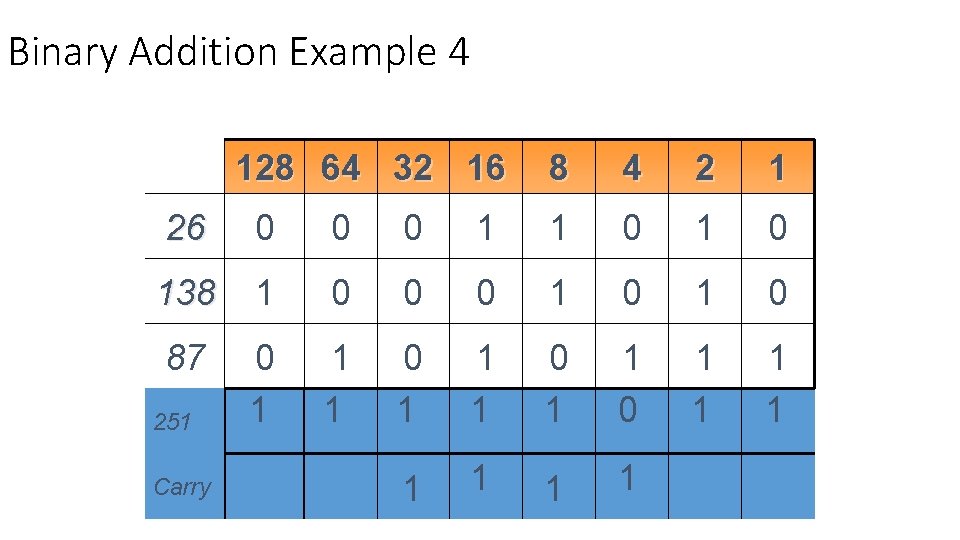
Binary Addition Example 4 128 64 32 16 8 4 2 1 26 0 0 0 1 1 0 138 1 0 0 0 1 0 87 0 1 1 1 1 1 251 Carry

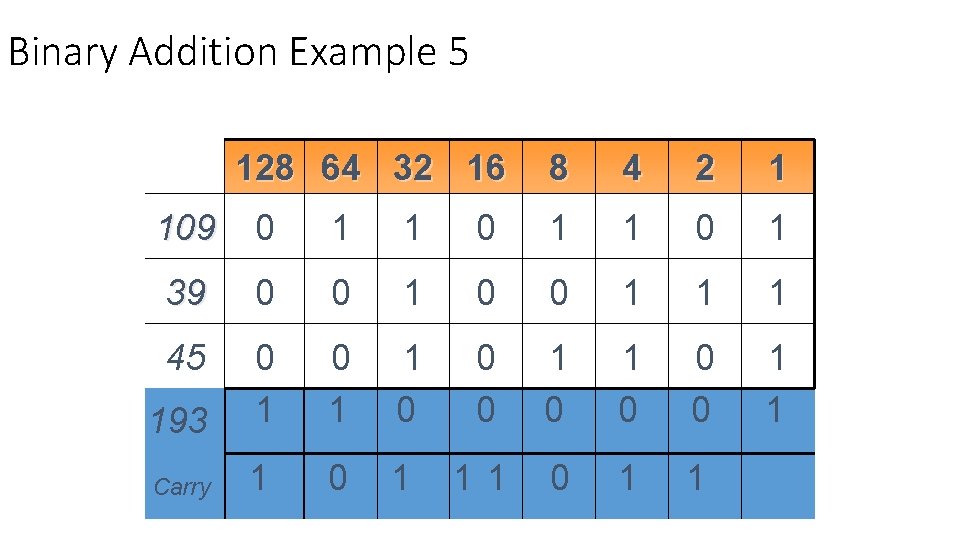
Binary Addition Example 5 128 64 32 16 8 4 2 1 109 0 1 1 0 1 39 0 0 1 1 1 45 193 0 1 1 0 0 0 1 1 Carry 1 0 1 1

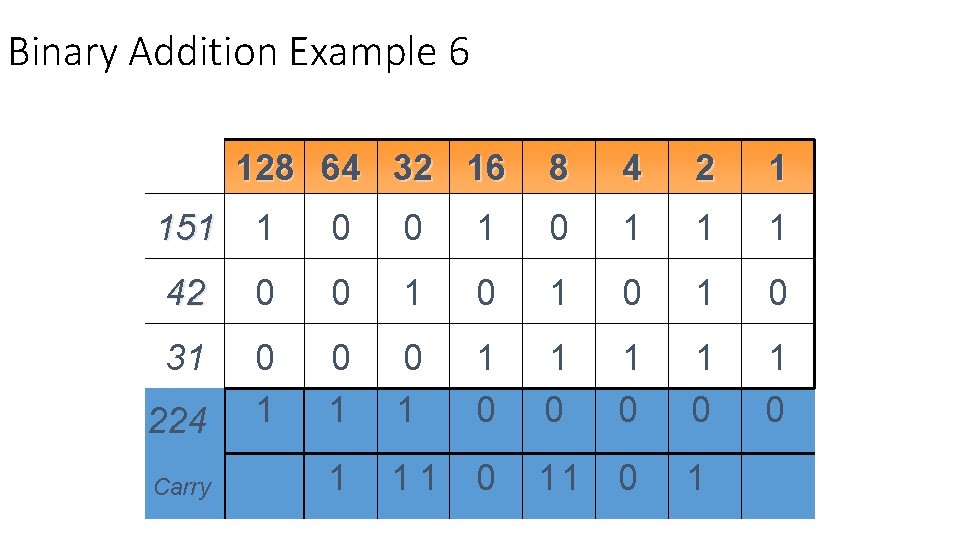
Binary Addition Example 6 128 64 32 16 8 4 2 1 151 1 0 0 1 1 1 42 0 0 1 0 1 0 31 0 1 0 1 11 0 1 224 Carry

Binary Subtraction • • • CPUs can’t subtract, they can only add! 75 -14=61 The same as… 75+(-14)=61 Positive + Negative = Negative • To do this we need 2 s Complement -128 64 32 16 8 4 2 1

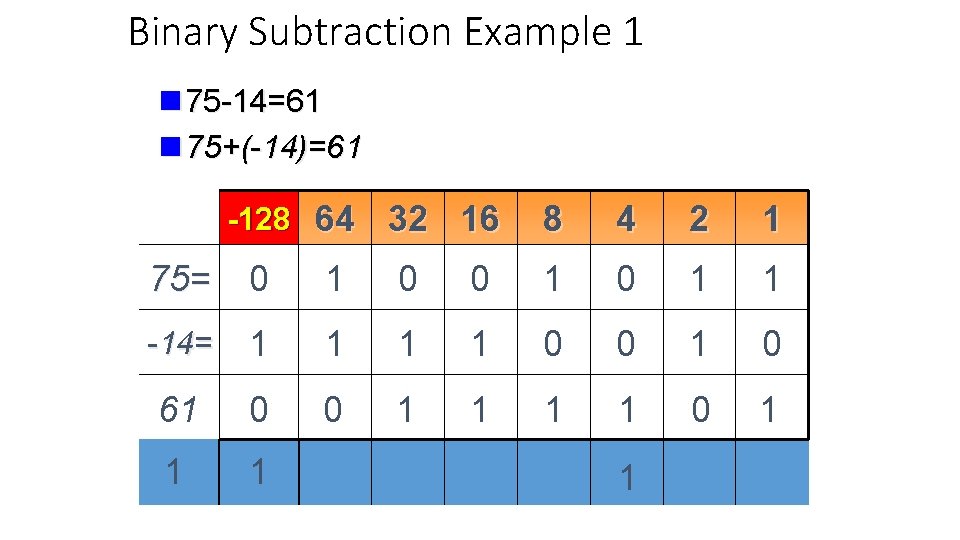
Binary Subtraction Example 1 n 75 -14=61 n 75+(-14)=61 -128 64 32 16 8 4 2 1 75= 0 1 0 1 1 -14= 1 1 0 0 1 0 61 0 0 1 1 1 1

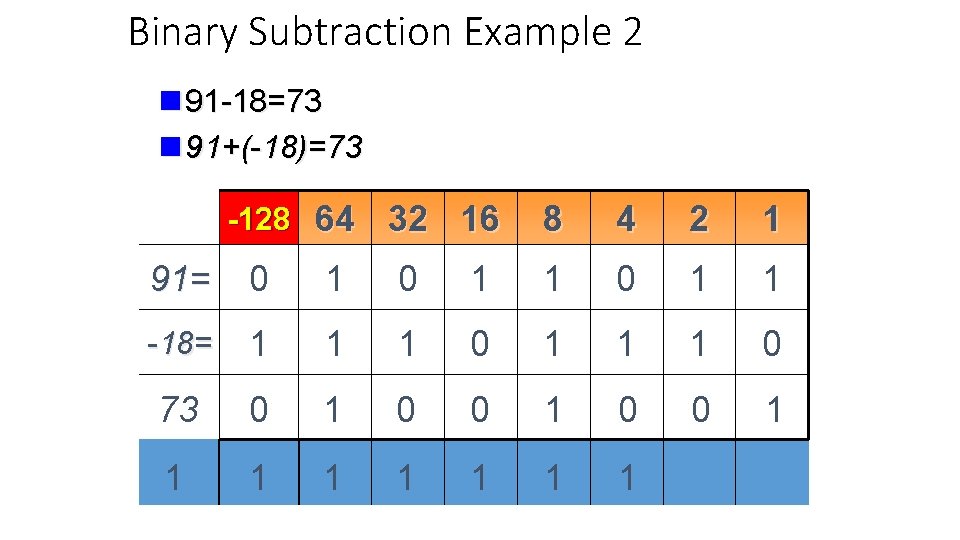
Binary Subtraction Example 2 n 91 -18=73 n 91+(-18)=73 -128 64 32 16 8 4 2 1 91= 0 1 1 -18= 1 1 1 0 73 0 1 0 0 1 1 1 1