Binary MergeSortA i j 01 if i j
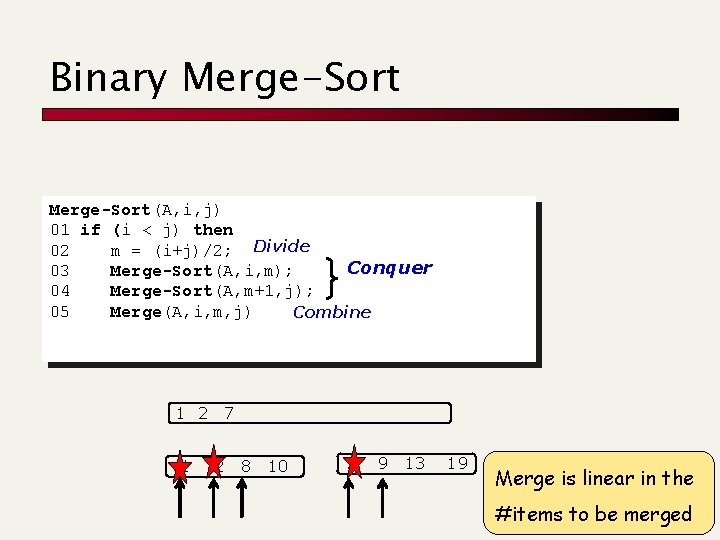
Binary Merge-Sort(A, i, j) 01 if (i < j) then 02 m = (i+j)/2; Divide Conquer 03 Merge-Sort(A, i, m); 04 Merge-Sort(A, m+1, j); 05 Merge(A, i, m, j) Combine 1 2 7 1 2 8 10 7 9 13 19 Merge is linear in the #items to be merged

Few key observations n Items = (short) strings = atomic. . . n On english wikipedia, about 109 tokens to sort n Q(n log n) memory accesses (I/Os ? ? ) n [5 ms] * n log 2 n ≈ 3 years In practice it is a “faster”, why?

Recursion 10 10 10 log 2 N 2 5 1 13 19 9 2 5 1 13 19 10 2 5 1 13 19 7 7 9 7 9 7 15 4 8 3 12 8 15 4 8 3 12 17 6 11 8 3 12 17 4 17 11 4 15 12 6 15 15 4 3 17 6 11 11
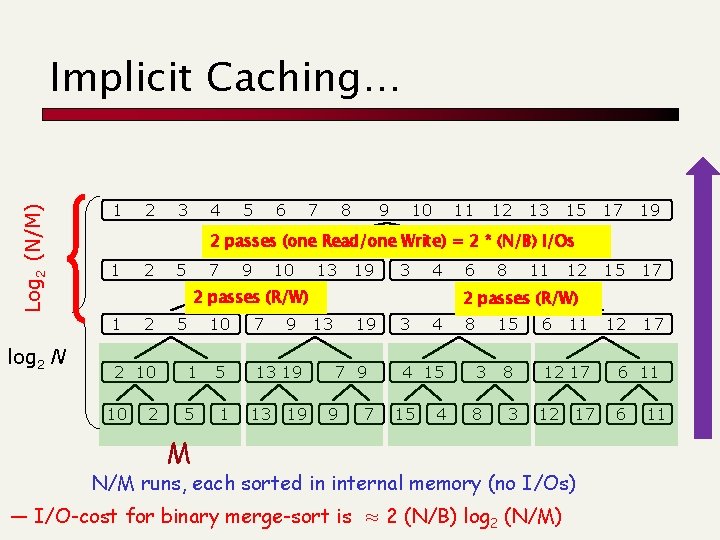
Log 2 (N/M) Implicit Caching… 1 3 4 5 6 7 8 9 10 11 12 13 15 17 19 15 17 12 17 2 passes (one Read/one Write) = 2 * (N/B) I/Os 1 2 5 7 9 10 13 19 3 4 2 passes (R/W) 1 log 2 N 2 2 2 10 10 2 5 10 7 9 1 5 13 19 5 1 13 19 6 8 11 12 2 passes (R/W) 13 19 7 9 9 7 3 4 4 15 15 4 8 15 6 11 3 8 12 17 8 3 12 17 M N/M runs, each sorted in internal memory (no I/Os) — I/O-cost for binary merge-sort is ≈ 2 (N/B) log 2 (N/M) 6 11
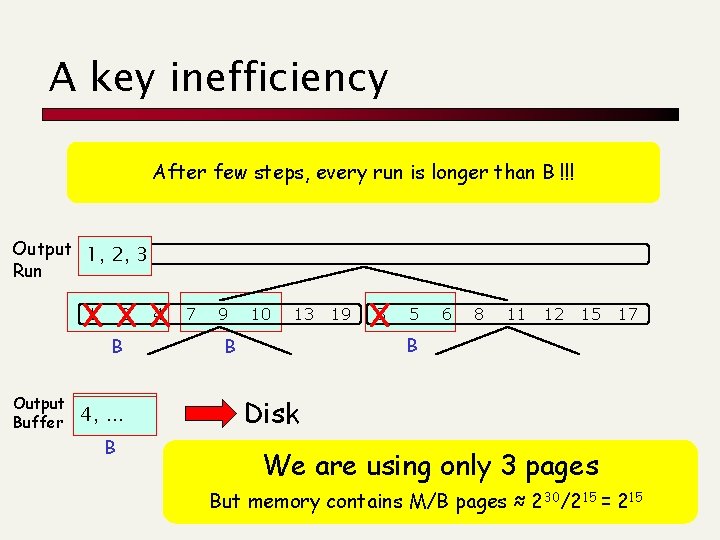
A key inefficiency After few steps, every run is longer than B !!! Output 1, 2, 3 Run 1 2 B Output Buffer 1, 4, 2, . . . 3 B 4 7 9 10 13 19 3 5 6 8 11 12 15 17 B B Disk We are using only 3 pages But memory contains M/B pages ≈ 230/215 = 215
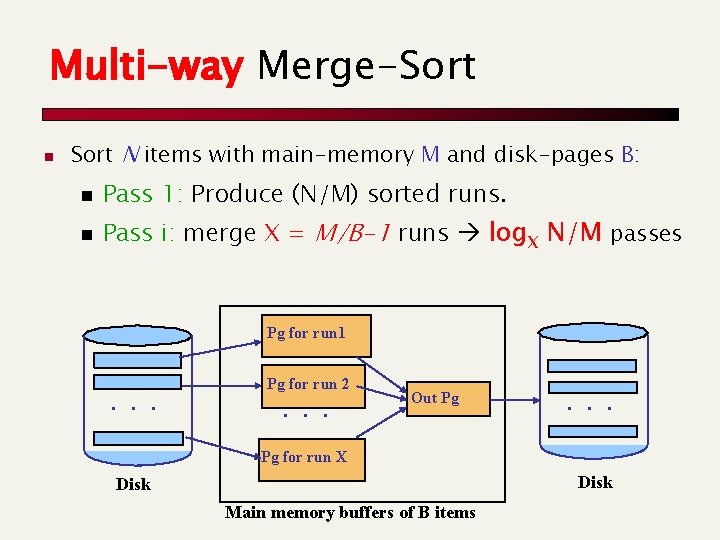
Multi-way Merge-Sort n Sort N items with main-memory M and disk-pages B: n Pass 1: Produce (N/M) sorted runs. n Pass i: merge X = M/B-1 runs log. X N/M passes Pg for run 1 . . . Pg for run 2 . . . Out Pg . . . Pg for run X Disk Main memory buffers of B items
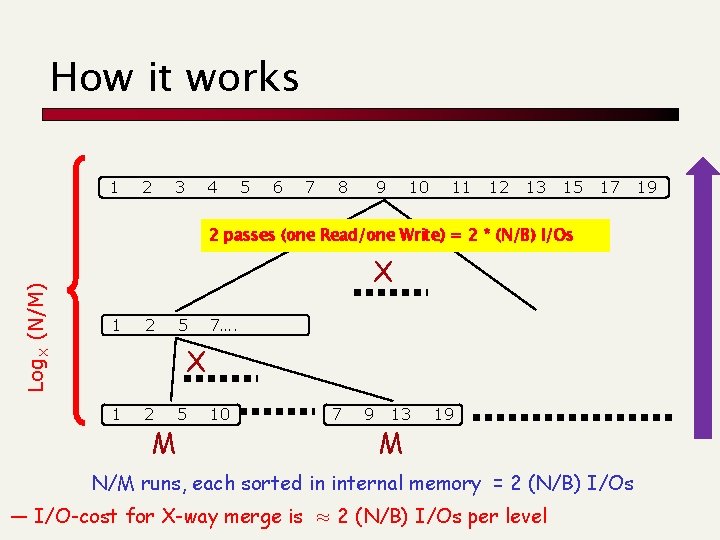
How it works 1 2 3 4 5 6 7 8 9 10 11 12 13 15 17 Log. X (N/M) 2 passes (one Read/one Write) = 2 * (N/B) I/Os X 1 2 5 7…. X 1 2 M 5 10 7 9 13 M 19 N/M runs, each sorted in internal memory = 2 (N/B) I/Os — I/O-cost for X-way merge is ≈ 2 (N/B) I/Os per level 19

Cost of Multi-way Merge-Sort n Number of passes = log. X N/M log. M/B (N/M) n Total I/O-cost is Q( (N/B) log. M/B N/M ) I/Os In practice n M/B ≈ 105 #passes =1 few mins Tuning depends on disk features ü Large fan-out (M/B) decreases #passes ü Compression would decrease the cost of a pass!
- Slides: 8