Binary Hex Binary and Hex The number systems

Binary / Hex Binary and Hex The number systems of Computer Science CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 1

Main Memory l Memory cells have two states: o On o Off Work best with two-state number system --- Binary number system l Investigate Decimal number system first l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 2

The Decimal Numbering System The decimal number system is a positional number system: the same digit will have different values in different positions. l Examples: 5 “five” = 5 * 1 l 50 500 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN “fifty” = 5 * 10 “five-hundred” = 5*100 3

The Decimal Numbering System Combinations yield any integer. l Example: 5621 1 X 1000 10 1 2 X 101 6 X 102 5 X 103 l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 4

What is the base ? The decimal numbering system is also known as base 10. The values of the positions are calculated by taking 10 to some power. l The common number system is a decimal or base 10 system because we use 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 5

What is the base ? The binary numbering system is called binary because it uses base 2. The values of the positions are calculated by taking 2 to some power. l The Binary system uses just two digits: 0 and 1 l A memory cell has just two states… (Can you feel the tension building? ) l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 6

The Binary Numbering System is also a positional numbering system. l Instead of ten digits, 0 - 9, the binary system uses only two digits, 0 and 1. l Example of a binary number & the values of the positions. 1 0 0 0 1 ( = 65) 2 6 2 5 2 4 23 2 2 21 2 0 l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 7

Computing the Decimal Values of Binary Numbers 1 0 0 0 1 2 6 2 5 2 4 23 2 2 21 2 0 20 = 1 21 = 2 22 = 4 23 = 8 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 24 = 16 25 = 32 26 = 64 1 X 20 = 1 0 X 21 = 0 0 X 22 = 0 0 X 23 = 0 0 X 24 = 0 0 X 25 = 0 1 X 26 = 64 65 8

Converting Decimal to Binary First make a list of the values of 2 to the powers of 0 to 8, then use the subtraction method. 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, 27 = 128, 28 = 256 l Example: 42 42 10 2 - 32 - 8 - 2 1 0 1 0 5 24 23 22 21 20 CMSC 104 Lecture 2 05 l Rev 99/09/19 PCOLSEN 9
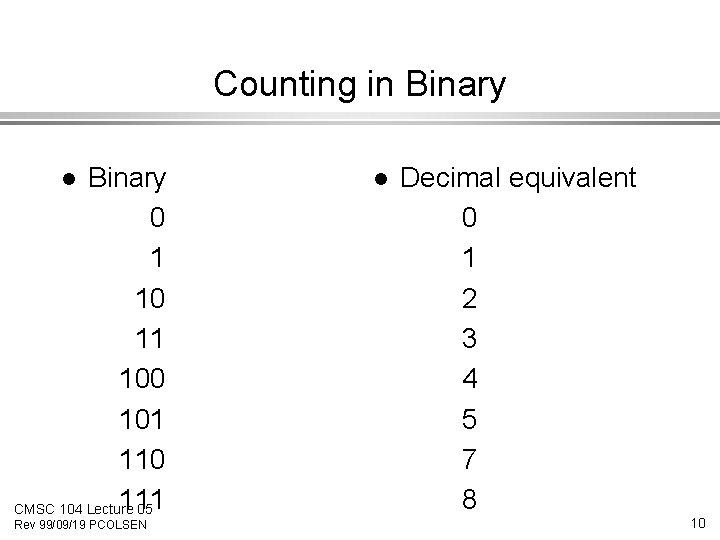
Counting in Binary 0 1 10 11 100 101 110 111 CMSC 104 Lecture 05 l Rev 99/09/19 PCOLSEN l Decimal equivalent 0 1 2 3 4 5 7 8 10

Addition of Binary Numbers l Examples: 1001 +0110 1111 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 0001 +1001 1010 1100 +0101 1 0001 11

Addition of Large Binary Numbers l Example showing larger numbers: 1010 0011 1011 0001 + 0111 0100 0001 1 0001 0111 1100 1010 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 12

Working with large numbers 0101 0000 1001 0111 Humans can’t work well with binary numbers. We will make errors. 110010111001101010 * 1100101 l Hexadecimal: Shorthand for binary l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 13

Hexadecimal Binary 0 1 0 0 1 1 1 Hex 5 Written: 509716 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 0 9 7 14

The Amazing Secret of Hexadecimal Notation! Binary 0 1 0 0 1 1 1 Hex 5 0 9 7 The amazing secret: 16 = 28 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 15

Hexadecimal Binary is base 2 two digits: 0, 1 l Decimal is base 10 ten digits: 0, 1, 3, 4, 5, 6, 7, 8, 9. l Hexadecimal (hex) is base 16. How many digits do we need to express numbers in hex? 16: 0 1 2 3 4 5 6 7 8 9 A B C D E F l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 16

Counting in Hex Binary 0000 0001 0010 0011 0100 0101 0110 0111 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN Hex 0 1 2 3 4 5 6 7 Binary 1000 1001 1010 1011 1100 1101 1110 1111 Hex 8 9 A B C D E F 17

Another Binary to Hex Conversion Binary 0 1 1 1 0 0 1 1 1 Hex 7 C 3 F 7 C 3 F 16 CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 18

Storing Negative Numbers in Binary Since we need to store negative numbers as well as positive numbers in binary, special variations on binary are used. l 2’s Complement notation is used for integers. l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 19

Building the 2’s Complement of a Binary Number Start with a binary number x = 1001 0101 l Replace 1 by 0, replace each 0 by 1 x 1 = 0110 1010 (“one’s complement”) l Add 1 to the least significant digit x 2 = 0110 1011 (“two’s complement”) l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 20

Why Two’s Complement? l Adding the two’s complement of a number is like subtracting the number x+x 2 = 1001 0101 + 0110 1011 1001 0110 1011 (1) 0000 where the leading 1 is in parentheses because it will be ignored. l Replaces Subtraction by Addition CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 21

Review The decimal, binary, and hexadecimal number systems are positional systems l The decimal number system has 10 digits, the binary system two, the hexadecimal system has 16 l The binary system is good system to use for two state memory devices. l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 22

Review The hexadecimal system (“hex”) needs 16 digits, so it uses 0 -9, A, B, C, D, E, F l The hexadecimal system is a often a convenient shorthand for the binary system: 4 -bits to one hex digit l Negative numbers are stored using “two’s complement” which turns subtraction into addition. l CMSC 104 Lecture 05 Rev 99/09/19 PCOLSEN 23
- Slides: 23