Binary Hex Binary and Hex The number systems

Binary / Hex Binary and Hex The number systems of Computer Science CMSC 104 1

Main Memory Capacitors on/off translates to values 1/0 l requires use of Binary number system l Investigate Decimal number system first l CMSC 104 2

The Decimal Numbering System The decimal numbering system is a positional number system. l Example: 5621 1 X 1000 10 1 2 X 101 6 X 102 5 X 103 l CMSC 104 3

What is the base ? The decimal numbering system is also known as base 10. The values of the positions are calculated by taking 10 to some power. l Why is the base 10 for decimal numbers ? l Because we use 10 digits. The digits 0 through 9. CMSC 104 4

What is the base ? The binary numbering system is called binary because it uses base 2. The values of the positions are calculated by taking 2 to some power. l Why is the base 2 for binary numbers ? l Because we use 2 digits. The digits 0 and 1. CMSC 104 5

The Binary Numbering System is also a positional numbering system. l Instead of using ten digits, 0 - 9, the binary system uses only two digits, the 0 and the 1. l Example of a binary number & the values of the positions. 1 0 0 0 1 CMSC 104 2 6 2 5 2 4 23 2 2 21 2 0 l 6

Computing the Decimal Values of Binary Numbers 1 0 0 0 1 2 6 2 5 2 4 23 2 2 21 2 0 20 = 1 21 = 2 22 = 4 23 = 8 CMSC 104 24 = 16 25 = 32 26 = 64 1 X 20 = 1 0 X 21 = 0 0 X 22 = 0 0 X 23 = 0 0 X 24 = 0 0 X 25 = 0 1 X 26 = 64 65 7

Converting Decimal to Binary First make a list of the values of 2 to the powers of 0 to 8, then use the subtraction method. 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64, 27 = 128, 28 = 256 l Example: 42 42 10 2 - 32 - 8 - 2 1 0 1 0 5 24 23 22 21 20 2 CMSC 104 l 8

Counting in Binary l CMSC 104 Binary 0 1 10 11 100 101 110 111 l Decimal equivalent 0 1 2 3 4 5 6 7 9

Addition of Binary Numbers l Examples: 1001 +0110 1111 CMSC 104 0001 +1001 1010 1100 +0101 1 0001 10

Addition of Large Binary Numbers l Example showing larger numbers: 1010 0011 1011 0001 + 0111 0100 0001 1 0001 0111 1100 1010 CMSC 104 11

Working with large numbers 0101 0000 1001 0111 Humans can’t work well with binary numbers. We will make errors. l Shorthand for binary that’s easier for us to work with - Hexadecimal l CMSC 104 12

Hexadecimal Binary 0 1 0 0 1 1 1 CMSC 104 Hex 5 Written: 509716 0 9 7 13

What is Hexadecimal really ? Binary 0 1 0 0 1 1 1 Hex 5 0 9 7 A number expressed in base 16. It’s easy to convert binary to hex and hex to binary because 16 is 24. CMSC 104 14

Hexadecimal Binary is base 2, because we use two digits, 0 and 1 l Decimal is base 10, because we use ten digits, 0 through 9. l Hexadecimal is base 16. How many digits do we need to express numbers in hex ? 16 (0 through ? ) l 0123456789 ABCDEF l CMSC 104 15
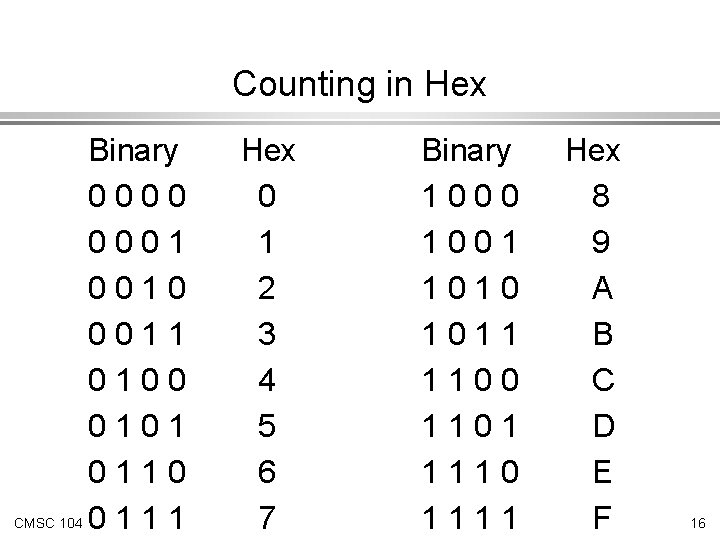
Counting in Hex Binary 0000 0001 0010 0011 0100 0101 0110 CMSC 104 0 1 1 1 Hex 0 1 2 3 4 5 6 7 Binary 1000 1001 1010 1011 1100 1101 1110 1111 Hex 8 9 A B C D E F 16

Another Binary to Hex Conversion Binary 0 1 1 1 0 0 1 1 1 Hex 7 C 3 F 7 C 3 F 16 CMSC 104 17
- Slides: 17