Binary heaps binary tree that satisfy two properties

Binary heaps • binary tree that satisfy two properties – structural property (is a complete tree) – heap-ordering property (minimum item on top) • Can have maximizing heaps too. 1

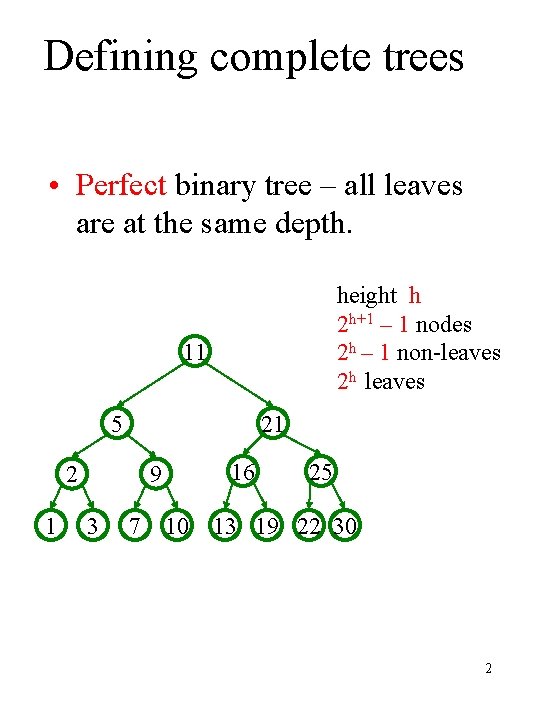
Defining complete trees • Perfect binary tree – all leaves are at the same depth. height h 2 h+1 – 1 nodes 2 h – 1 non-leaves 2 h leaves 11 5 2 1 21 9 3 7 10 16 25 13 19 22 30 2

Defining complete trees (2) • Complete trees, informally: A perfect binary tree of height h-1 with leaves added at height h in the leftmost positions. N-node complete tree of height h: h = log N 2 h N 2 h+1 - 1 3

Complete binary tree of height h • For h = 0, just a single node. • For h = 1, left child or two children. • For h 2, either – the left subtree of the root is perfect with height h-1 and the right is complete with height h-1, OR – the left is complete with height h 1 and the right is perfect with height h-2. 4

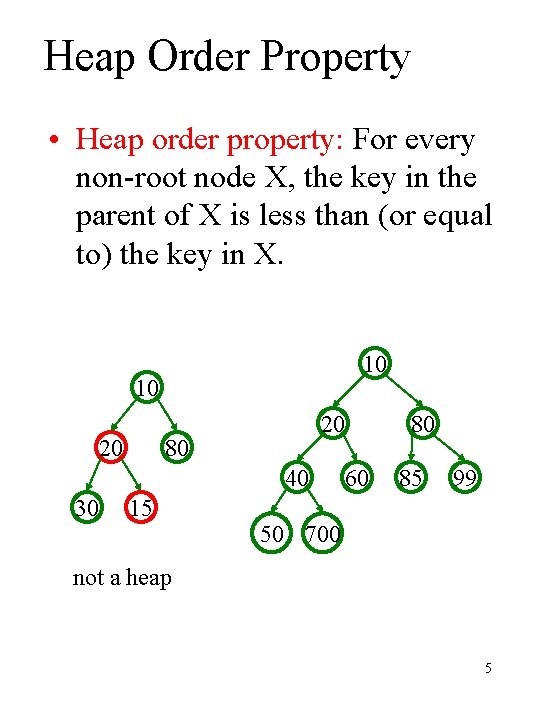
Heap Order Property • Heap order property: For every non-root node X, the key in the parent of X is less than (or equal to) the key in X. 10 10 20 20 80 40 30 15 80 60 85 99 50 700 not a heap 5

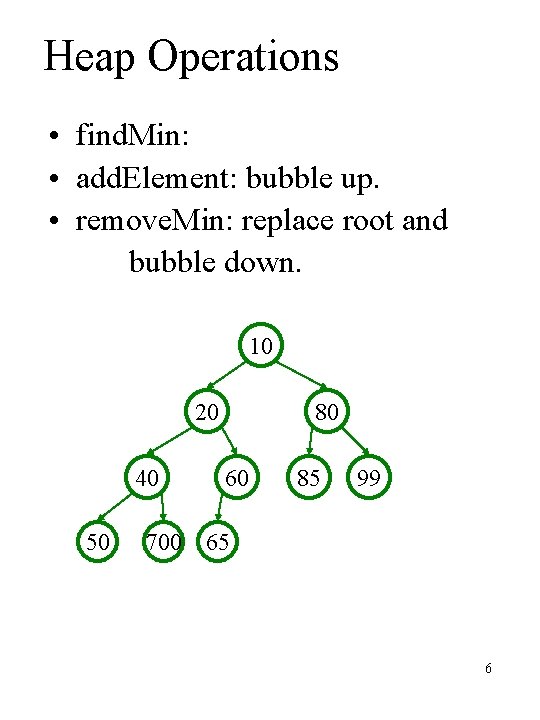
Heap Operations • find. Min: • add. Element: bubble up. • remove. Min: replace root and bubble down. 10 20 40 50 80 60 85 99 700 65 6

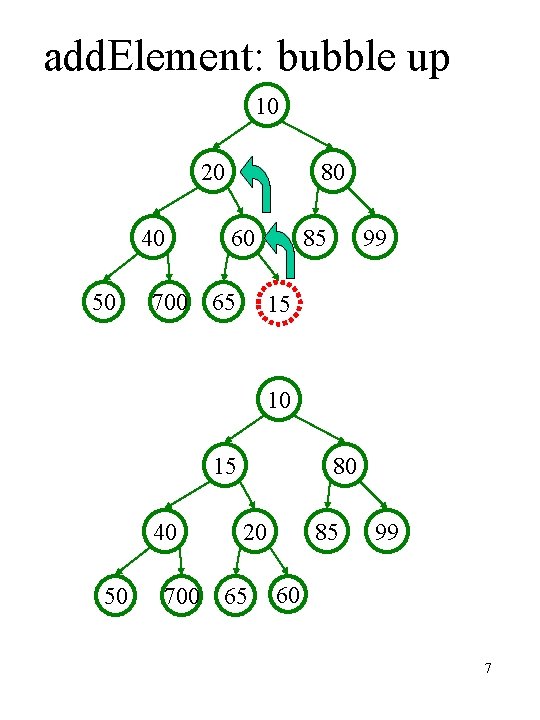
add. Element: bubble up 10 20 40 50 80 60 700 65 85 99 15 10 15 40 50 80 20 700 65 85 99 60 7

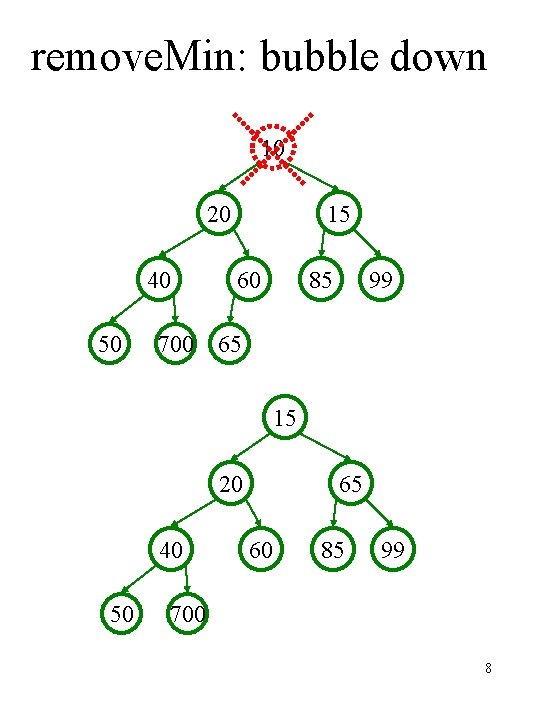
remove. Min: bubble down 10 20 40 50 15 60 85 99 700 65 15 20 40 50 65 60 85 99 700 8

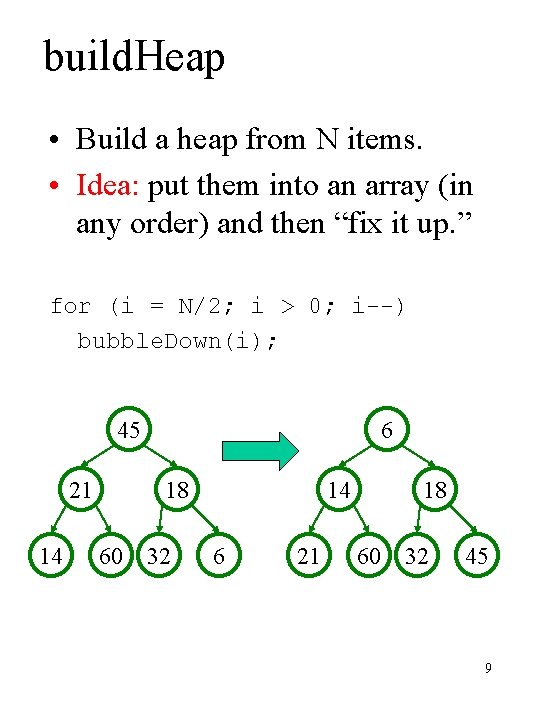
build. Heap • Build a heap from N items. • Idea: put them into an array (in any order) and then “fix it up. ” for (i = N/2; i > 0; i--) bubble. Down(i); 45 21 14 6 18 60 32 14 6 21 18 60 32 45 9

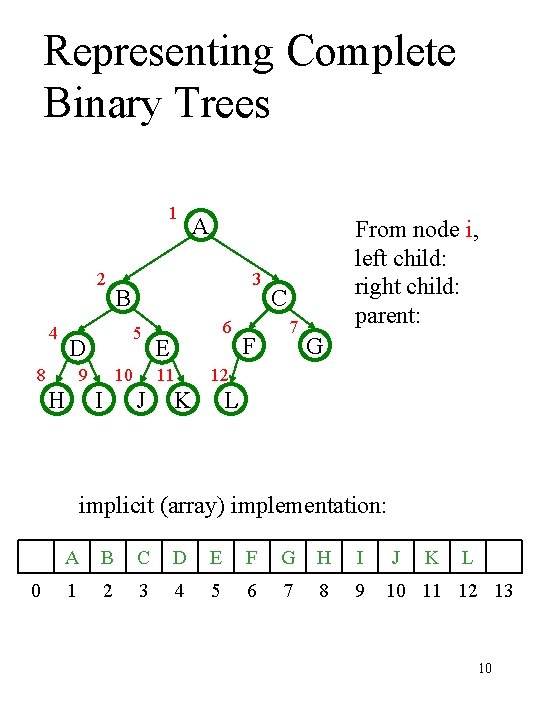
Representing Complete Binary Trees 1 2 4 3 B 5 D 8 9 H 10 I A 6 E 11 J F From node i, left child: right child: parent: C 7 G 12 K L implicit (array) implementation: 0 A B C D E F G H I 1 2 3 4 5 6 7 8 9 J K L 10 11 12 13 10

Why is it better? • no pointers (space). • *2, /2, + are faster operations than dereferencing a pointer. • can get to parent easily • Can we use the implicit representation for binary search trees? 11

Analysis of build. Heap • An item that starts h nodes from a leaf moves down at most h nodes during its bubbling phase. • Let S be the sum of the heights of all the nodes in a perfect binary tree. = h + 2(h-1) + 4(h-2) + … + 2 h-1 · 1 2 S = 2 h + 4(h-1) + … + 2 h-1 · 2 + 2 h · 1 S = – h + 2 + 4 + 8 + … + 2 h-1 + 2 h = 2 h+1 – (h+1) N 12

Heaps (summary) • add. Element: bubble up. O(log N) time. • remove. Min: bubble down. O(log N) time. • build. Heap: for N items, O(N) time. • Heapsort: – build. Heap on N items O(N) – N remove. Min ops O(N log N) 13

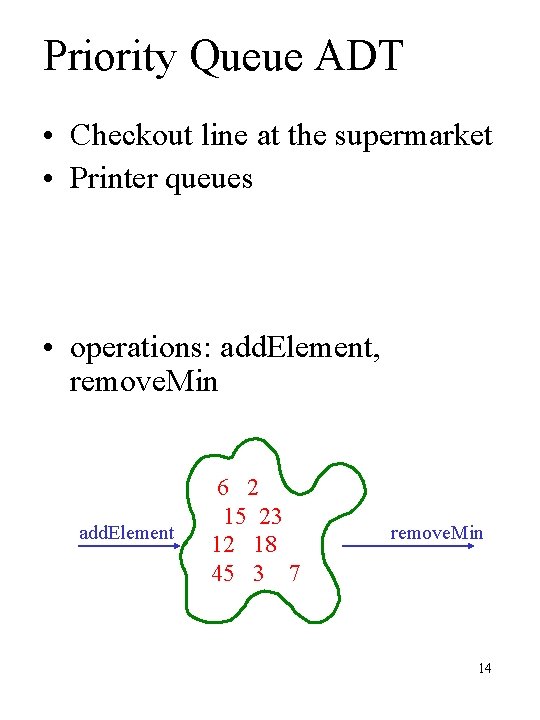
Priority Queue ADT • Checkout line at the supermarket • Printer queues • operations: add. Element, remove. Min add. Element 6 2 15 23 12 18 45 3 7 remove. Min 14

Simplementations of the Priority Queue ADT insert delete. Min (unsorted) list sorted list BST AVL tree (overkill? ) 15

Other PQ Operations • decrease. Key(p, ): bubble up • increase. Key(p, ): bubble down • remove(p): decrease. Key(p, ) delete. Min() Running time: O(log N) • find. Max: O(N). 16

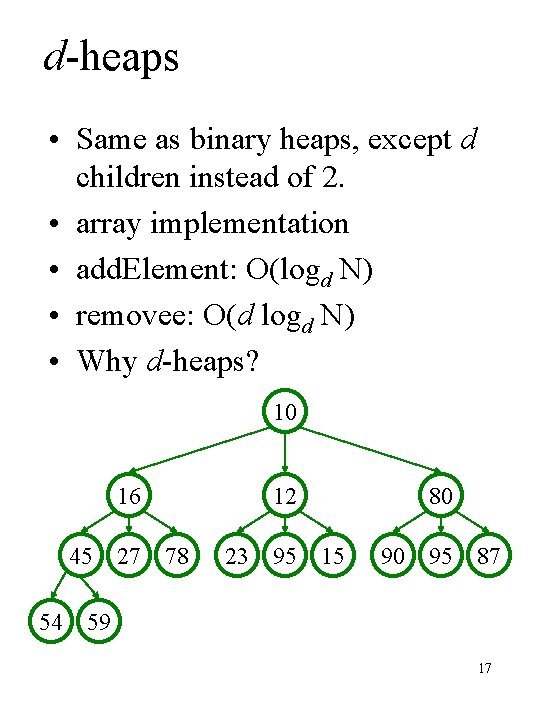
d-heaps • Same as binary heaps, except d children instead of 2. • array implementation • add. Element: O(logd N) • removee: O(d logd N) • Why d-heaps? 10 16 45 27 78 12 23 95 80 15 90 95 87 54 59 17