Binary Expression Trees a data structure used to

Binary Expression Trees (a data structure used to store algebraic expressions) infix expression: parenthesize fully: a / b + (c - d) * e ((a / b) + ((c - d) * e)) **Each binary expression (within parentheses) can be represented by a tree where the root is the operator and the children are the operands. ** + / a * b c e d

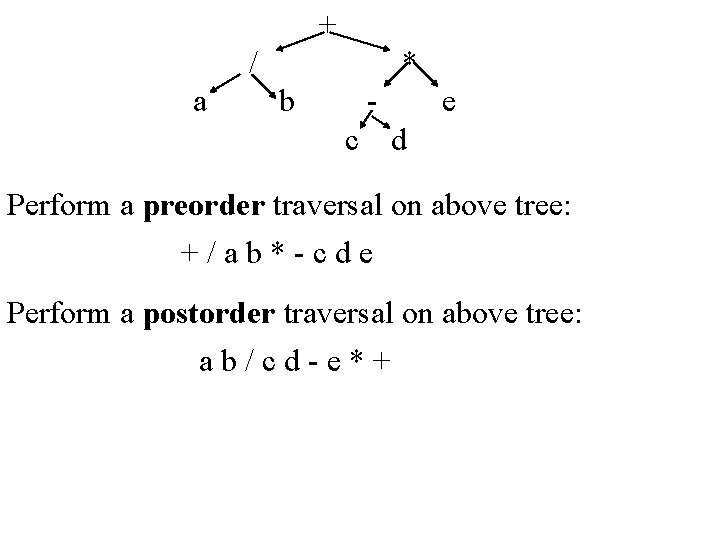
+ / a * b c e d Perform a preorder traversal on above tree: +/ab*-cde Perform a postorder traversal on above tree: ab/cd-e*+

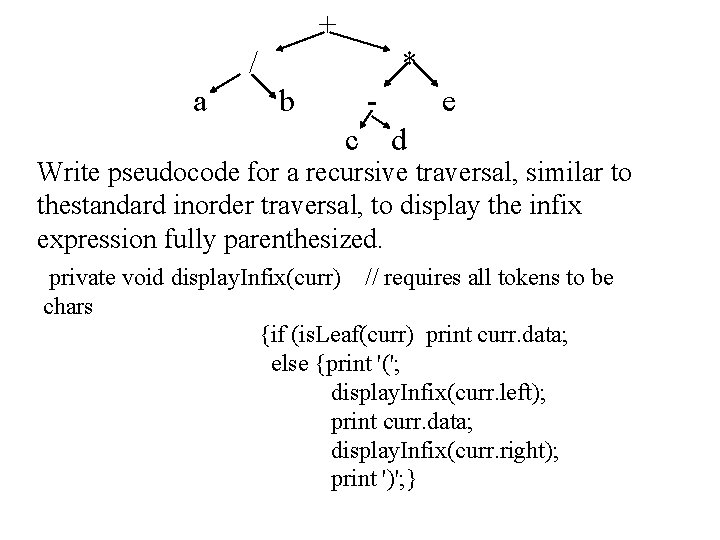
+ / a * b c e d Write pseudocode for a recursive traversal, similar to thestandard inorder traversal, to display the infix expression fully parenthesized. private void display. Infix(curr) // requires all tokens to be chars {if (is. Leaf(curr) print curr. data; else {print '('; display. Infix(curr. left); print curr. data; display. Infix(curr. right); print ')'; }

Write pseudocode for a recursive method that evaluates a binary expression tree. private int eval. Tree(curr) //assumes operands are strings { if is. Leaf(curr) return Integer. parse. Int(curr. data); else { switch curr. data case '*': return eval. Tree(curr. left) * eval. Tree(curr. left): break; case '/': return eval. Tree(curr. left) / eval. Tree(curr. left): break; case '+': return eval. Tree(curr. left) + eval. Tree(curr. left): break; case '-': return eval. Tree(curr. left) - eval. Tree(curr. left): break; } }