Binary Encoding under Functional Symmetry GIEE NTU ALCom

Binary Encoding under Functional Symmetry GIEE, NTU ALCom Lab Presenter: Meng-yen Li

Outline Some definitions Binary Encoding Problem 1 -MI-1 -BO Problem 1 -MI-1 -MO Problem p-MI-1 -BO Problem p-MI-1 -MO Problem Other Related Problem

Definitions Symmetry: {X 1, X 2} denote if f(X) has functional symmetry of first and second variable input. f 01 X = f 10 X , where x is a cube. (e. g. f 01110, x is 110) fi denote cofactor of i-th minterm. Full Symmetry: f has full symmetry if f has symmetries of all variable pairs. Minterms with same number of 1 s need mapped to same value in f.

Full Symmetry Example f(a, b, c): B 3→B has FS if {X 1, X 2}: f 2 = f 4 , f 3 = f 5 {X 2, X 3}: f 1 = f 2 , f 5 = f 6 {X 3, X 1}: f 1 = f 4 , f 3 = f 6 FS f 1 = f 2 = f 4 , f 3 = f 5 = f 6 f 1, f 2, f 4 have one “ 1” in minterm f 3, f 5, f 6 have two “ 1” in minterm a b c f 0 0 0 f 0=0 0 0 1 f 1=1 0 f 2=1 0 1 1 f 3=0 1 0 0 f 4=1 1 0 1 f 5=0 1 1 0 f 6=0 1 1 1 f 7=1

Full Symmetry Properties f(a, b, c): B 3→B has FS f 1 = f 2 = f 4 , f 3 = f 5 = f 6 There’s C 30 of minterms have 0 number of “ 1” in them. There’s C 3 i of minterms have i number of “ 1” in them. There’s C 33 of minterms have 3 number of “ 1” in them. Minterms with same number of 1 s need mapped to same value in f f has full symmetry

Binary Encoding Problem Given a function f, we want to encode its input variable in some way to let f has some property(like full symmetry). To be more specific, we classify the problem into 4 types. 1 -MI-1 -BO problem 1 -MI-1 -MO problem p-MI-1 -BO problem p-MI-1 -MO problem

Illustration of BE Problem Given function K=3 F 3(X): N→B, X {N | 0 X 7=23 -1}, encode X’s values into 3 bits of binary variables X 1, X 2, X 3. Let FB 3 (X 1, X 2, X 3) : B 3→B, FB 3 has same functionality as F 3(X). X F 3 X 1 X 2 X 3 FB 3 0 1 0 0 0 1 1 1 0 0 0 1 1 0 2 1 0 1 1 0 0 1 0 1 3 1 0 1 1 1 0 1 0 1 4 0 1 0 0 0 1 0 1 1 0 0 5 1 1 0 0 1 1 6 0 1 1 0 0 7 0 1 1 1 0 0 0 1 1 1 0 Given function table Encoding that don’t have FS Encoding that has FS Not encoding at all

Formalizing 1 -MI-1 -BO Problem Statement: Given function Fk(X): N→B, X {N | 0 X m-1, m=2 k} as a mapping table, encode X into k bits of binary variables X 1, X 2, …, Xk. (F has total m minterms, and mi denote i-th minterm) Let FBk (X 1, X 2, …, Xk) : Bk→B be the encoded function, FBk has same functionality as Fk(X). Q 1: Is there existing an encoding that makes FBk has full symmetry over X 1, X 2, …, Xk? Q 2: If yes, generate one.

1 -MI-1 -BO: Concept of Solution In short: We don’t need to fill variables in the encoded table to express the 1 -MI-1 -BO problem. The solution is yes if number of Fk’s onset(offset) minterm can be expressed as summation of Cki.

1 -MI-1 -BO: Concept of Solution In detail: FBk (X 1, X 2, …, Xk) has FS: the minterms in encoding have same number of 1 s need to map to same value of outputs. So an encoding has FS number of every output value can be a summation of some combination of Cki. For example, k=3 X 1 X 2 X 3 FB 3 C 3 3 1 1 0 C 3 2 1 0 0 1 0 1 C 3 1 1 0 0 0 1 1 C 3 0 1 1 0 0 0 Encoding that have FS

1 -MI-1 -BO: Concept of Solution It can be further reduced to knapsack problems. This reduction only apply to 1 -MI-1 -BO problem Because we can change the encoding of each minterm freely. Also F only have 2 value of outputs(0 and 1). The solution is reduced to “If knapsack P 1 can exactly contain some items of Cki , then there exist an encoding of X makes F has FS. ” P 1 is the number of minterms mapped to 1. C 3 0 C 3 1 C 3 2 C 3 0 3 P 1 C 3 1

1 -MI-1 -BO: Formalizing Solution We can formulate the FS condition for solution as an ILP constraint problem. Objective: Minimize Constraint Y 1: 0 Variables: (1 constraint is needed) (k+1 binary variables are needed) P 1, Cki need to be given/computed before using ILP solver.

1 -MI-1 -BO: Solution Example X F 3 K=3, m=8, P 1=4 X 1 X 2 X 3 FB 3 0 0 0 1 1 0 0 0 2 1 0 1 1 1 3 1 1 0 1 1 4 0 minimize 0 0 1 0 0 5 1 1 1 0 1 6 0 a 0=1, a 1=0, a 2=1, a 0=0 is one solution of ai in this ILP problem. 0 0 1 0 7 0 000, 011, 101, 110 is onset of F 1 1 1 0 Given function table Encoding that have FS

Formalizing 1 -MI-1 -MO Problem Statement: Given function Y=Fk(X): N→N, X {N | 0 X m-1, m=2 k}, Y {N | 0 Y mout-1, mout=2 n} as a mapping table, encode X into k and Y into n bits of binary variables X 1, X 2, …, Xk; Y 1, Y 2, …, Yn Let FBk (X 1, X 2, …, Xk) : Bk→Bn be the encoded function, FBk has same functionality as Fk(X). Let Yn(X 1, X 2, …, Xk): Bk→B be the n-th output binary function. Q 1: Is there existing an encoding that makes all Yn has full symmetry over X 1, X 2, …, Xk? Q 2: If yes, generate one.
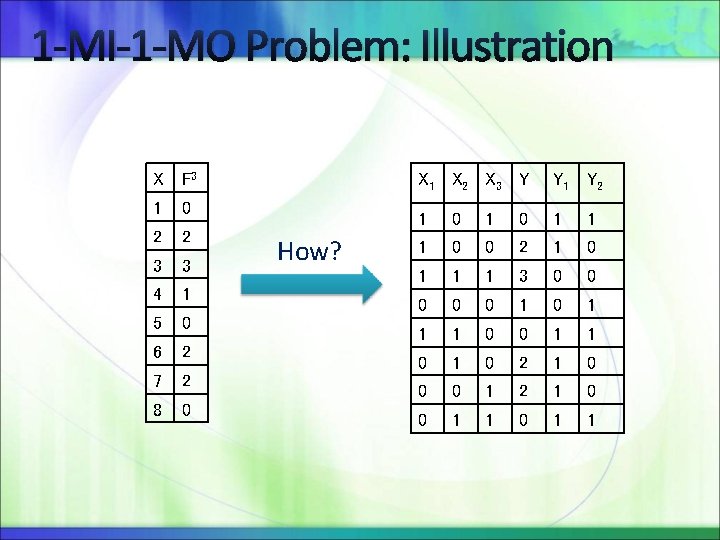
1 -MI-1 -MO Problem: Illustration X F 3 1 0 2 2 3 3 4 1 5 0 6 2 7 2 8 0 How? X 1 X 2 X 3 Y Y 1 Y 2 1 0 1 1 1 0 0 2 1 0 1 1 1 3 0 0 0 1 1 1 0 0 1 1 0 2 1 0 0 0 1 2 1 0 0 1 1

1 -MI-1 -MO: Concept of Solution In short: For X variable’s encoding bits, we still don’t need to use variable to constraint them and express the constraint, because we still can freely change encoding at X side. But on Y side, we need to use binary variable to represent the encoding. So the solution is, for each Yn functon check if number of Yn’s onset(offset) minterm can be expressed as summation of Cki. And check if those Y variables are a valid encoding.

1 -MI-1 -MO: Concept of Solution For each Y’s value, use b. C(m_out) to represent. C for n-th Y function column(to avoid confused with 2 n output minterms’s n). mout_i for (out_i)-th output variable minterm X Y Y 1 Y 2 0 0 b 10 b 20 1 2 b 12 b 22 2 3 b 13 b 23 3 1 b 11 b 21 4 0 b 10 b 20 5 2 b 12 b 22 6 2 b 12 b 22 7 0 b 10 b 20 Pmout_i is the number of minterms mapped to value mout_i P 0=3 P 1=1 P 2=3 P 3=1

1 -MI-1 -MO: Concept of Solution For those b. C(m_out) variables really define an encoding, we will need encoding constraint. For each output minterm pair(j, h), j h Y Y 1 Y 2 0 b 10 b 20 1 b 11 b 21 2 b 12 b 22 3 b 13 b 23 That is, in the encoding table for Y variable, no two different values are mapped to same encoding Thus the summation of difference of two rows in the table must 1.

1 -MI-1 -MO: Concept of Solution But we still need to convert the absolute value summation to ILP form. For each C from 1 to n, add auxiliary variable ZCjh And the summation need > 0 for difference b. Cj b. Ch b. Cj+b. Ch ZC 2 ZC-(b. Cj+b. Ch) 0 0 0 1 1 1 2 1 0

1 -MI-1 -BO: Formalizing Solution We can formulate the FS condition for solution as an ILP constraint problem. Objective: Minimize Constraint Y 1 to Yn: (n constraints) 0 Constraint Encoding: ( constraint) Variable: (n*(k+1)’s a, n*(2 n)’s b , ‘s Z variables) Pm_out, Cki need to be given/computed before using ILP solver.

Formalizing p-MI-1 -BO Problem Statement: Given function Y=Fk(X 1, X 2, …XP): →B, X 1 {N | 0 X 1 m 1 -1, m 1=2 k 1}, … Xp {N | 0 Xp mp-1, mp=2 kp} , k=k 1+k 2+…+kp, as a mapping table, encode X 1 into k 1 … and Xp into kp bits of binary variables X 11, X 12, …, X 1 k 1; …; Xp 1, Xp 2, …, Xpkp Let FBk (X 11, X 12, …, X 1 k 1; …; Xp 1, Xp 2, …, Xpkp) : Bk→B be the encoded function, FBk has same functionality as Fk(X 1, X 2, …XP). Q 1: Is there existing an encoding that makes FBk has full symmetry over (X 11, X 12, …, X 1 k 1; …; Xp 1, Xp 2, …, Xpkp)? Q 2: If yes, generate one.
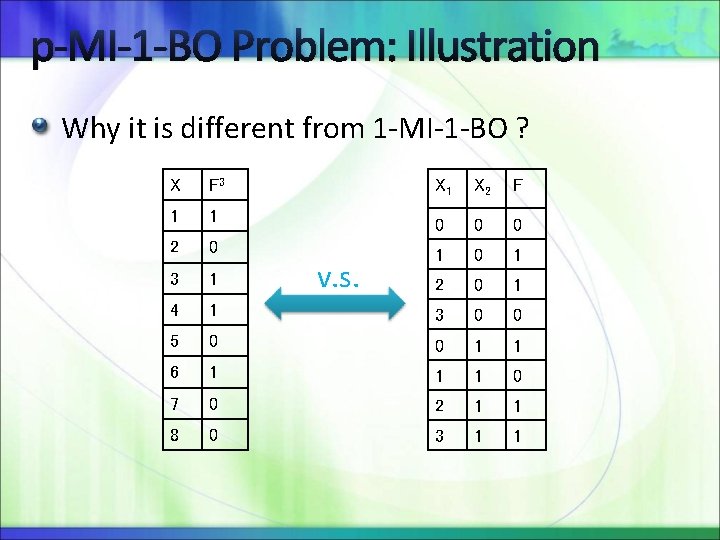
p-MI-1 -BO Problem: Illustration Why it is different from 1 -MI-1 -BO ? X F 3 X 1 X 2 F 1 1 0 0 0 2 0 1 3 1 2 0 1 4 1 3 0 0 5 0 0 1 1 6 1 1 1 0 7 0 2 1 1 8 0 3 1 1 v. s.

p-MI-1 -BO Problem: Illustration We can no longer freely swap encoding at X side! X F 3 X 1 X 2 F 1 1 0 0 0 2 0 1 3 1 2 0 1 4 1 3 0 0 5 0 0 1 1 6 1 1 1 0 7 0 2 1 1 8 0 3 1 1 8! number of possible encoding 4!*2!

p-MI-1 -BO Problem: Solution To simplify the problem, we only discuss the case p = 2. Define the X side variable to represent encoding. Condition for F has FS: 1. the X variables are valid encoding for X 1. 2. the X variables are valid encoding for X 2. 3. the X variables are valid encoding for X. (trivially satisfied if 1 & 2 is satisfied) 4. minterms with same # of 1 s are mapped to same output value(in BO, it’s onset or offset).
![p-MI-1 -BO Problem: Solution Define the X variables as Xpe[B] : p represent for p-MI-1 -BO Problem: Solution Define the X variables as Xpe[B] : p represent for](http://slidetodoc.com/presentation_image_h2/c77ae7e654b0b77ccbc58dc545fb32ea/image-25.jpg)
p-MI-1 -BO Problem: Solution Define the X variables as Xpe[B] : p represent for Xp e represent for e-th minterm’s encoding for Xp B represent B-th bit for e-th minterm X 1 X 2 Y X 10 [0] X 10 [1] X 20 [0] 1 X 11 [0] X 11 [1] X 20 [0] 0 X 12 [0] X 13 [1] X 20 [0] 1 X 13 [0] X 14 [1] X 20 [0] 1 X 10 [0] X 10 [1] X 21 [0] 0 X 11 [0] X 11 [1] X 21 [0] 1 X 12 [0] X 12 [1] X 21 [0] 0 X 13 [0] X 13 [1] X 21 [0] 0

p-MI-1 -BO Problem: Solution To simplify the problem, we only discuss the case p = 2. For X 1 and X 2, the X variables need be valid encoding. For each minterm pair(j 1, h 1), j 1 h 1, j 1, h 1 in X 1 For each minterm pair(j 2, h 2), j 2 h 2, j 2, h 2 in X 2

p-MI-1 -BO Problem: Solution To express the constraint for “same # of 1 s minterm are mapped to same value” is a little tricky when involving with X variables. a and b are two different rows in X encoding because fa and fb is given is the table, this constraint only correspond to a constraint with single absolute value notation.

p-MI-1 -BO Problem: Solution How to figure out this constraint? The constraint we want is “# of 1 s same fa=fb” recall that p q ~p q # of 1 s not same: difference of encoding is 1 because it’s BO, there’s a trick, |fa-fb| is at most 1. ~p q output same? # of 1 s same? above formula yes, 0 (0 – 0 = 0) 0 yes, 0 no, 1 (0 – 1) = 0 no, 1 yes, 0 (1 – 0 = 1) not 0 no, 1 no, 1 (1 – 1) = 0

p-MI-1 -BO Problem: Solution Convert to linear constraint |fa-fb|pre-caculated as RHS. Conver to summation of each bit difference So we can use the same technique convert to linear constraint before.

p-MI-1 -BO: Formalizing Solution We can formulate the FS condition for solution as an ILP constraint problem. Objective: Minimize 0 Constraint X 1 : for each pair minterm(j 1, h 1) in X 1 for each B 1 from 0 to k 1 -1 Constraint X 2: for each pair minterm(j 2, h 2) in X 2 for each B 2 from 0 to k 2 -1

p-MI-1 -BO: Formalizing Solution Constraint FS: for each pair minterm(a, b) in X for each bit B 1=0 to k 1 -1, B 2=0 to k 2 -1 constraints Note that ZB 1 j 1 h 1 != ZB 1 ab (why? ) X 1 X 2 Y X 10 [0] X 10 [1] X 20 [0] 1 … … X 10 [0] X 10 [1] X 21 [0] 0 X 11 [0] X 11 [1] X 21 [0] 1

p-MI-1 -BO: Formalizing Solution Variables 2 K 1*K 1 2 K 2*K 2 X 1 variables X 2 variables ZB 1 j 1 h 1 variables ZB 1 j 2 h 2 variables ZBab variables

Formalizing p-MI-1 -MO Problem Statement: Given function Y=Fk(X 1, X 2, …XP): →N, X 1 {N | 0 X 1 m 1 -1, m 1=2 k 1}, … Xp {N | 0 Xp mp-1, mp=2 kp} , k=k 1+k 2+…+kp, Y {N | 0 Y mout-1, mout=2 n} as a mapping table, encode X 1 into k 1 … and Xp into kp bits of binary variables X 11, X 12, …, X 1 k 1; …; Xp 1, Xp 2, …, Xpkp ; Y 1, Y 2, …, Yn Let FBk (X 11, X 12, …, X 1 k 1; …; Xp 1, Xp 2, …, Xpkp) : Bk→B be the encoded function, FBk has same functionality as Fk(X 1, X 2, …XP). Let Yn(X 1, X 2, …, Xk): Bk→B be the n-th output binary function.

p-MI-1 -MO Problem: Illustration A more complicate problem X 1 X 2 Y Y 1 Y 2 X 10 [0] X 10 [1] X 20 [0] 0 b 10 B 20 X 11 [0] X 11 [1] X 20 [0] 2 b 12 b 22 X 12 [0] X 12 [1] X 20 [0] 3 b 13 b 23 X 13 [0] X 13 [1] X 20 [0] 1 b 11 b 21 X 10 [0] X 10 [1] X 21 [0] 0 b 10 b 20 X 11 [0] X 11 [1] X 21 [0] 2 b 12 b 23 X 12 [0] X 12 [1] X 21 [0] 2 b 12 b 22 X 13 [0] X 13 [1] X 21 [0] 0 b 10 b 20

p-MI-1 -MO Problem: Solution 1. Condition that X 1, X 2, Y are all valid encoding: 2. Condition that for each Yn has FS: …

More on 1 -MI-1 -BO problem In the 1 -MI-1 -BO problem we know that it is reduced to knapsack problem. Given the number of on-set minterms of f, we can compute if this number has solution or not. Can we know if all the number have a solution?

More on 1 -MI-1 -BO problem For example, in k=3 problem We can derive the Pascal Triangle numbers first C 30 = 1, C 31=3, C 32=3, C 33=1 The possible number of minterms are from 0 to 23=8 X F 3 0 1 1 0 2 1 3 1 4 0 5 1 6 0 7 0 #On-set minterm = 4 = 1+3(has solution)

More on 1 -MI-1 -BO problem For example, in k=3 problem And we can know that in k=3, always have solution for BE problem that has FS. #on-set minterm sol 0 0 1 1 2 1+1 3 3 4 3+1 5 1+1+3 6 3+3 7 1+3+3 8 1+3+3+1

More on 1 -MI-1 -BO problem For example, in k=4 problem(1, 4, 6, 4, 1) There’s some number that cannot be a summation of the Pascal numbers. #m sol 0 0 16 1+4+6+4+1 1 1 15 1+4+6+4 2 1+1 14 4+6+4 3 no solution 13 no solution 4 4 12 1+6+4+1 5 4+1 11 1+4+6 6 4+1+1 10 4+4+1+1 7 6+1 9 4+4+1 8 1+1+6

More on 1 -MI-1 -BO problem For example, in k=5 problem(1, 5, 10, 5, 1) # sol 0 y 9 n 1 y 10 y 2 y 11 y 3 n 12 y 4 n 13 n 5 y 14 n 6 y 15 y 7 y 16 y 8 n Why we don’t list the entire table? Why it is list to 16? What’s the property of no solution numbers?

More on 1 -MI-1 -BO problem For example, in k=5 problem(1, 5, 10, 5, 1) # sol 0 y 9 n 1 y 10 y Solution m=2 k-m 2 y 11 y Why it is list to 16? 3 n 12 y 4 n 13 n 5 y 14 n 6 y 15 y 7 y 16 y 8 n Why we don’t list the entire table? Same as above, and 2 k-1 must sol=yes What’s the property of no solution numbers? I can’t find a formula, if you can, please tell me! There’s some property for some basic case, like between 3 ~ k-1, and other summation of possible combination with number between 3 ~ k-1, but the later is more difficult to solve because it may overlap with other possible summation

More on 1 -MI-1 -BO problem For a given k problem. Definiton 1: T is the target number, 0 T 2 k, T is covered if and only if , where ai is binary variables T is covered T has encoding for FS Definition 2: If all number T, 0 T 2 k, are covered, we say those numbers are k-covered and has Sk symmetry. For example, 0 ~ 8 is 3 -covered and has S 3.

More on 1 -MI-1 -BO problem Definiton 3: If some number T, 0 T 2 k, T is not k-covered, then we “degrade” it to (k-d)-covered, where 0 d k For example, k=4 , T=3 is degrade to 3 -covered. Lemma 1: The condition to degrade to be covered by k-d is C 3 0 C 2 0 C 3 1 C 2 1 C 3 2 C 2 1 Split to 2 d (k-d)-Pascal -numbers C 3 3 C 2 0

More on 1 -MI-1 -BO problem Definiton 4: We only say 0 T 2 k, are (k-d)-covered if the d is the minimum number that can cover all number in 0 T 2 k. That is, 0 T 2 k, are not (k-d+1)-covered. And trivially, 0 -covered to (k-d-1)-covered.

More on 1 -MI-1 -BO problem Theorem 1: Given k, 0 T 2 k are at least (k-d)-covered. Where k d k-d 1 0 1 8 2 6 2 0 2 9 2 7 3 0 3 10 2 8 4 1 3 11 2 9 5 1 4 12 3 9 6 1 5 13 3 10 7 2 5 14 3 11

More on 1 -MI-1 -BO problem Theorem 1: Given k, 0 T 2 k are at least (k-d)-covered. Where Proof: 2 d 2 d+1 k-d possible k-d range Suppose we degrade to k-d 0~2 d is covered because there are 2 d Ck-d 0. 0~2 d+1 is covered because there are 2 d (Ck-d 0+ Ck-dk-d). k-d’s possible range is shown as above When k-d=2 d+1+1 is the maximum coverage that kd can cover.

More on 1 -MI-1 -BO problem Theorem 1: Given k, 0 T 2 k are at least (k-d)-covered. Where Proof: 2 d 2 d+1 k-d 0~2 d+1+1=k-d is covered because k-d=Ck-d 1 Thus we “fill up” all the point between Ck-d 0 to Ck-d 1 Because there are 2 d Ck-d 1, so up to Ck-d 2 can be filled by previous Ck-d 1.

More on 1 -MI-1 -BO problem Theorem 1: Given k, 0 T 2 k are at least (k-d)-covered. Where Proof: 0 2 d+1 k-d Ck-d 1 2 d Ck-d 1 Similarly, we can prove that all numbers are covered if 0 to k-d is covered. Ck-d 2
- Slides: 48