Binary Decision Diagrams and Symbolic Model Checking Randy

Binary Decision Diagrams and Symbolic Model Checking Randy Bryant Ed Clarke Ken Mc. Millan Allen Emerson CMU Cadence U Texas http: //www. cs. cmu. edu/~bryant

Binary Decision Diagrams Restricted Form of Branching Program n Graph representation of Boolean function n Canonical form Simple algorithms to construct & manipulate n Application Niche n n Problems expressed as Quantified Boolean Formulas A lot of interesting problems are in PSPACE Symbolic Model Checking n n – 2 – Prove properties about large-scale, finite-state system Successfully used to verify hardware systems

Boolean Function as Language Truth Table Language { 011, 101, 111 } DFA 0 1 1 0, 1 1 n n – 3 – View n-variable Boolean function as language {0, 1}n Reduced DFA is canonical representation

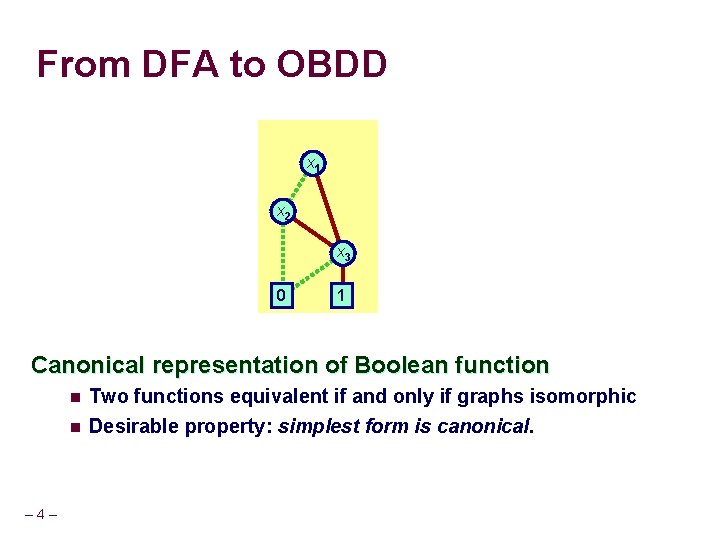
From DFA to OBDD 0 x 1 x 2 1 0, 1 x 3 1 1 Canonical representation of Boolean function – 4 – n Two functions equivalent if and only if graphs isomorphic n Desirable property: simplest form is canonical.

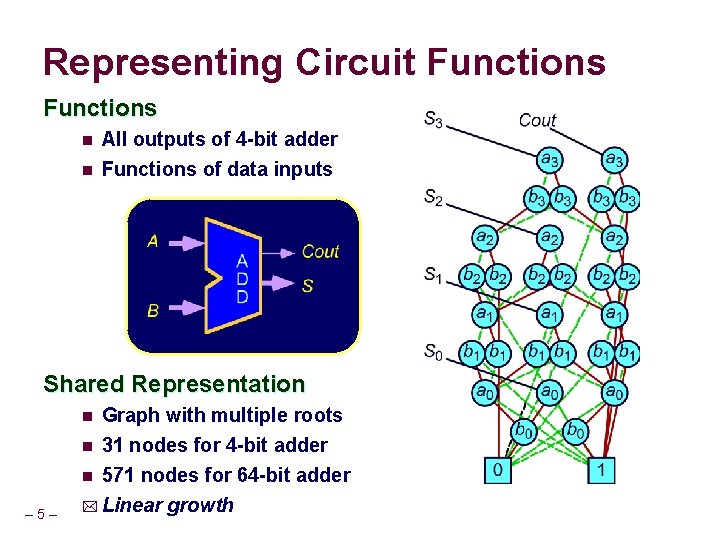
Representing Circuit Functions n All outputs of 4 -bit adder n Functions of data inputs Shared Representation n 31 nodes for 4 -bit adder n 571 nodes for 64 -bit adder * Linear growth n – 5 – Graph with multiple roots

Effect of Variable Ordering Good Ordering Linear Growth – 6 – Bad Ordering Exponential Growth

Sample Function Classes Function Class Best Worst Ordering Sensitivity ALU (Add/Sub) linear exponential High Symmetric linear quadratic None Multiplication exponential Low General Experience n Many tasks have reasonable OBDD representations n Algorithms remain practical for up to 500, 000 node OBDDs Heuristic ordering methods generally satisfactory n – 7 –

Symbolic Manipulation with OBDDs Strategy n Represent data as set of OBDDs l Identical variable orderings n Express solution method as sequence of symbolic operations l Sequence of constructor & query operations l Similar style to on-line algorithm n Implement each operation by OBDD manipulation l Do all the work in the constructor operations Key Algorithmic Properties n n n – 8 – Arguments are OBDDs with identical variable orderings Result is OBDD with same ordering Each step polynomial complexity

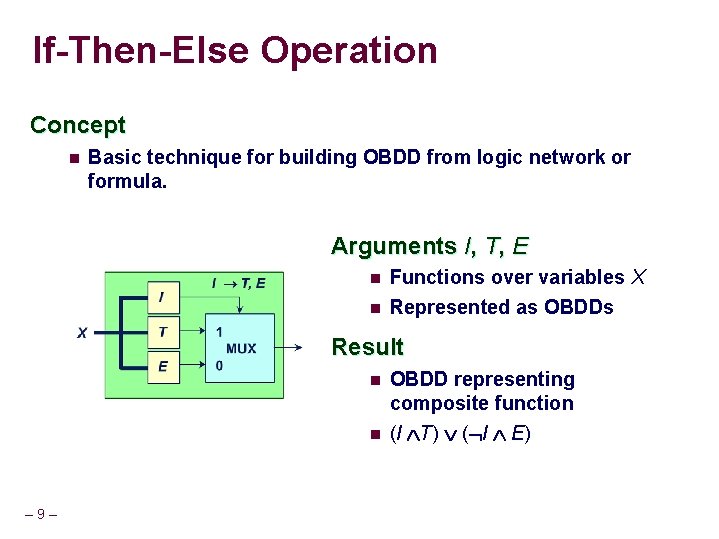
If-Then-Else Operation Concept n Basic technique for building OBDD from logic network or formula. Arguments I, T, E n Functions over variables X n Represented as OBDDs Result n n – 9 – OBDD representing composite function (I T) ( I E)

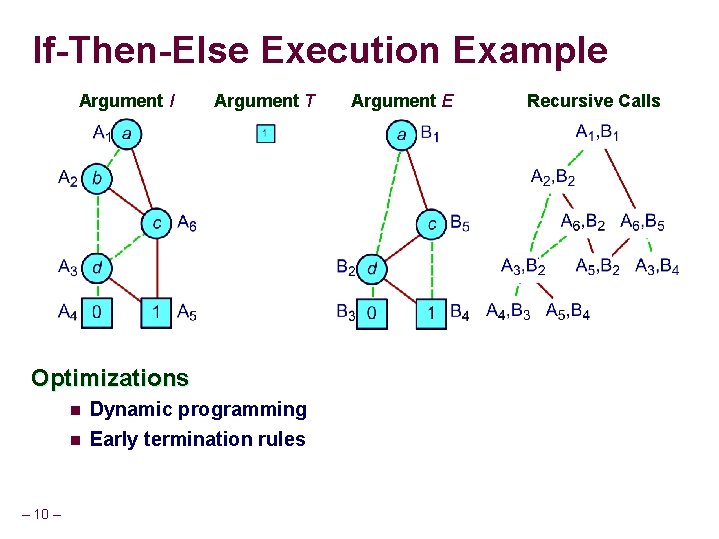
If-Then-Else Execution Example Argument I Argument T Optimizations – 10 – n Dynamic programming n Early termination rules Argument E Recursive Calls

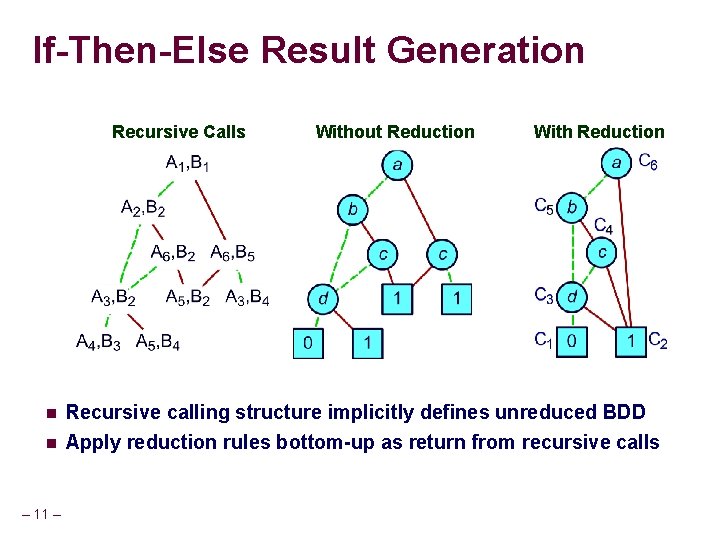
If-Then-Else Result Generation Recursive Calls n n – 11 – Without Reduction With Reduction Recursive calling structure implicitly defines unreduced BDD Apply reduction rules bottom-up as return from recursive calls

Restriction Operation Concept – 12 – n Effect of setting function argument xi to constant k (0 or 1). n Also called Cofactor operation (UCB)

Restriction Execution Example Argument F Restriction F[b=1] a Reduced Result a b c d 0 – 13 – d d 1 c c 0 1

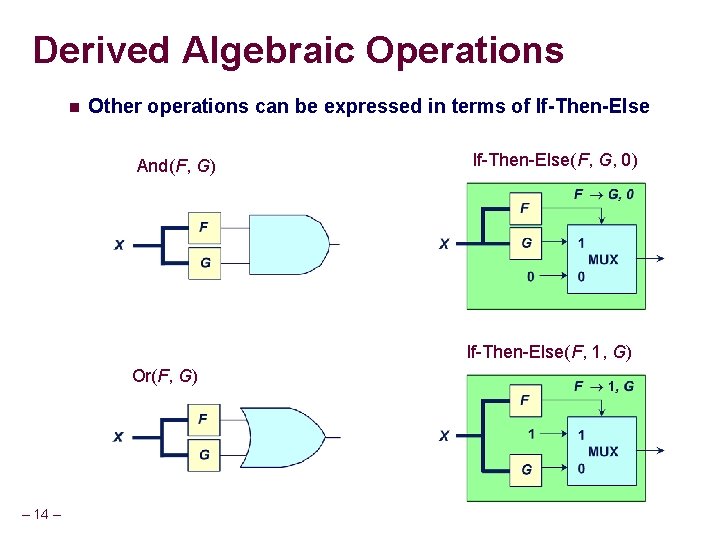
Derived Algebraic Operations n Other operations can be expressed in terms of If-Then-Else And(F, G) If-Then-Else(F, G, 0) If-Then-Else(F, 1, G) Or(F, G) – 14 –

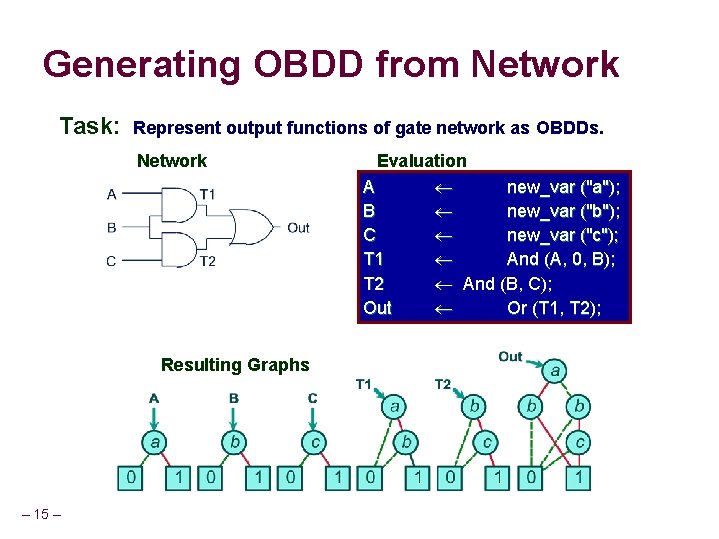
Generating OBDD from Network Task: Represent output functions of gate network as OBDDs. Network Resulting Graphs – 15 – Evaluation A new_var ("a"); B new_var ("b"); C new_var ("c"); T 1 And (A, 0, B); T 2 And (B, C); Out Or (T 1, T 2);

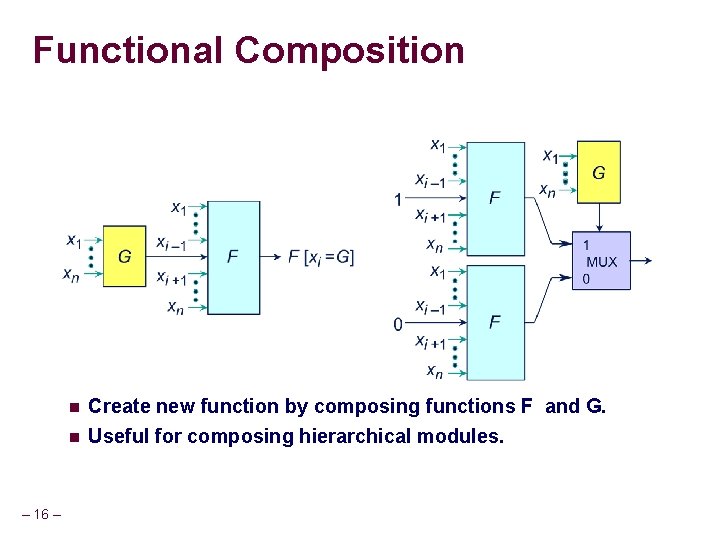
Functional Composition n n – 16 – Create new function by composing functions F and G. Useful for composing hierarchical modules.

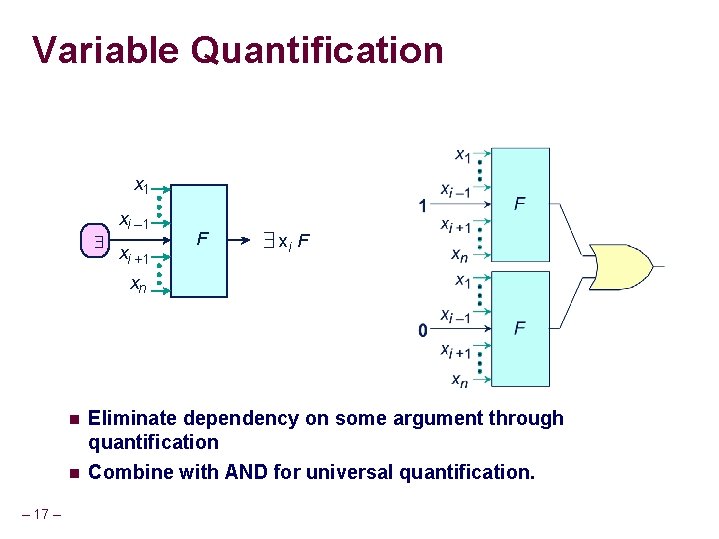
Variable Quantification x 1 $ xi – 1 xi +1 F $ xi F xn – 17 – n Eliminate dependency on some argument through quantification n Combine with AND for universal quantification.

Finite State System Analysis Systems Represented as Finite State Machines n Sequential circuits n Communication protocols Synchronization programs n Analysis Tasks n n n State reachability State machine comparison Temporal logic model checking Traditional Methods Impractical for Large Machines n n n – 18 – Polynomial in number of states Number of states exponential in number of state variables. Example: single 32 -bit register has 4, 294, 967, 296 states!

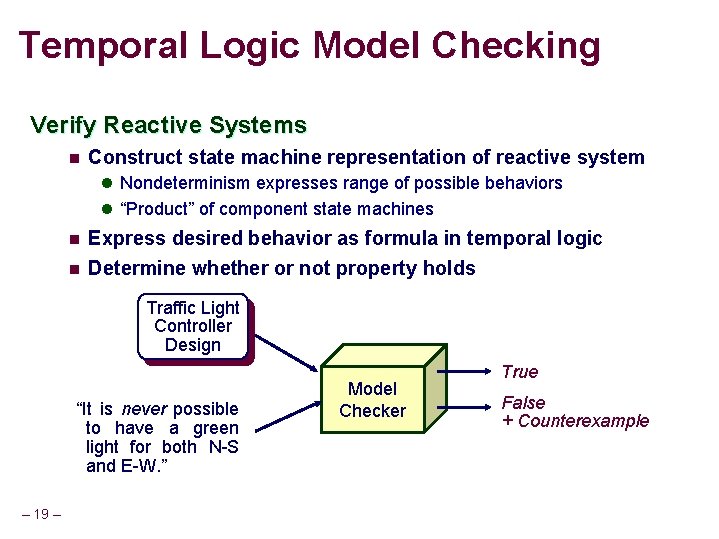
Temporal Logic Model Checking Verify Reactive Systems n Construct state machine representation of reactive system l Nondeterminism expresses range of possible behaviors l “Product” of component state machines n n Express desired behavior as formula in temporal logic Determine whether or not property holds Traffic Light Controller Design “It is never possible to have a green light for both N-S and E-W. ” – 19 – Model Checker True False + Counterexample

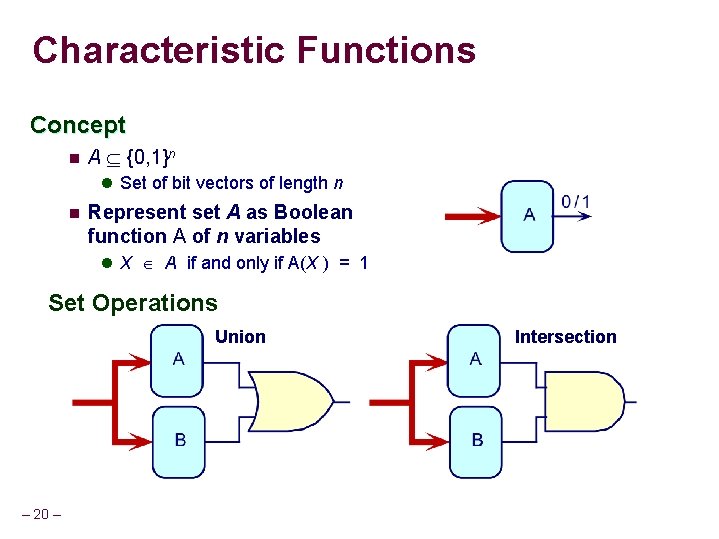
Characteristic Functions Concept n A {0, 1}n l Set of bit vectors of length n n Represent set A as Boolean function A of n variables l X A if and only if A(X ) = 1 Set Operations Union – 20 – Intersection

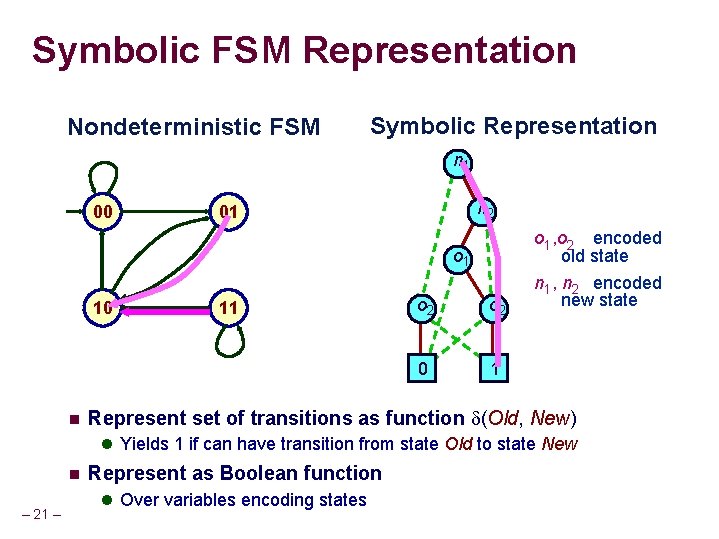
Symbolic FSM Representation Nondeterministic FSM Symbolic Representation n 1 00 n 2 01 o 1 10 n 11 o 2 0 1 o 1 , o 2 encoded old state n 1 , n 2 encoded new state Represent set of transitions as function (Old, New) l Yields 1 if can have transition from state Old to state New n – 21 – Represent as Boolean function l Over variables encoding states

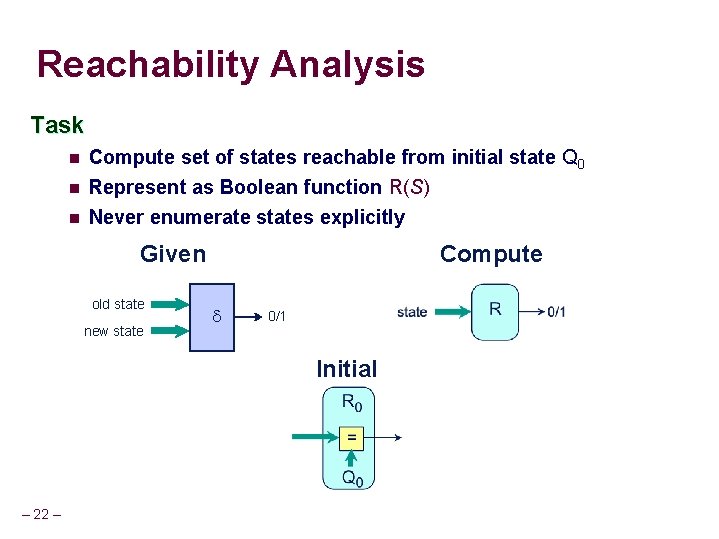
Reachability Analysis Task n Compute set of states reachable from initial state Q 0 n Represent as Boolean function R(S) Never enumerate states explicitly n Given old state new state Compute 0/1 Initial – 22 –

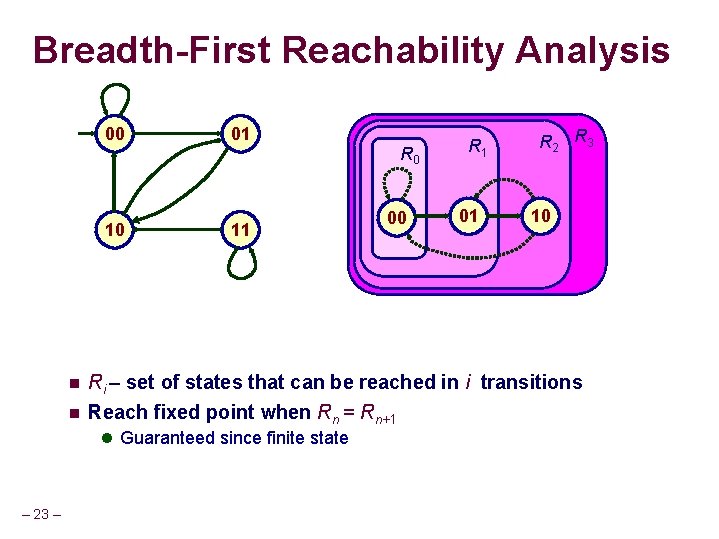
Breadth-First Reachability Analysis 00 01 R 0 10 n n 11 01 R 2 R 3 10 Ri – set of states that can be reached in i transitions Reach fixed point when Rn = Rn+1 l Guaranteed since finite state – 23 – 00 00 R 1

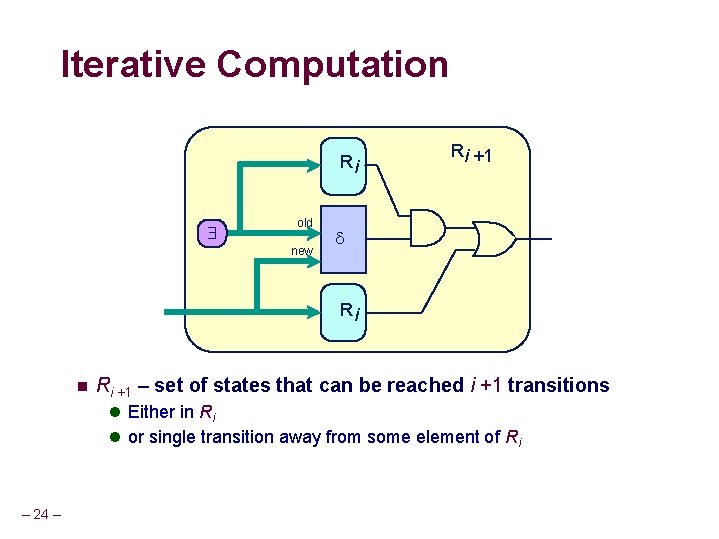
Iterative Computation Ri $ old new Ri +1 Ri n Ri +1 – set of states that can be reached i +1 transitions l Either in Ri l or single transition away from some element of Ri – 24 –

Symbolic FSM Analysis Example n K. Mc. Millan, E. Clarke (CMU) J. Schwalbe (Encore Computer) Encore Gigamax Cache System n n n Distributed memory multiprocessor Cache system to improve access time Complex hardware and synchronization protocol. Verification n n Create “simplified” finite state model of system (109 states!) Verify properties about set of reachable states Bug Detected n n n – 25 – Sequence of 13 bus events leading to deadlock With random simulations, would require 2 years to generate failing case. In real system, would yield MTBF < 1 day.

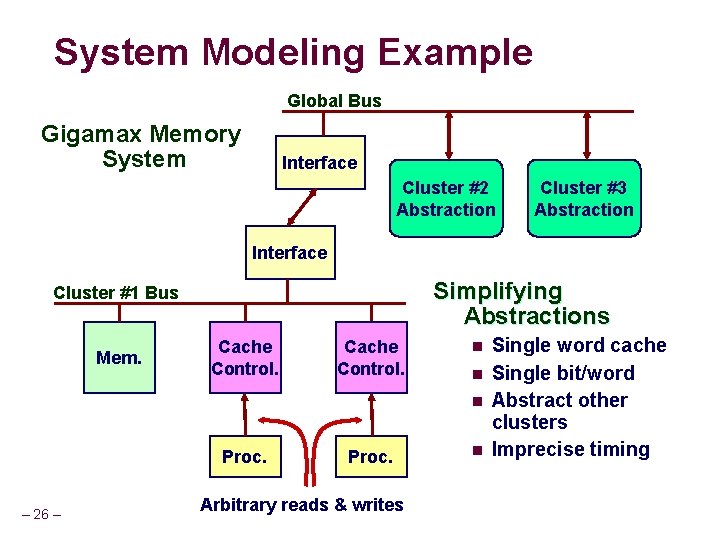
System Modeling Example Global Bus Gigamax Memory System Interface Cluster #2 Abstraction Cluster #3 Abstraction Interface Simplifying Abstractions Cluster #1 Bus Mem. Cache Control. n n n Proc. – 26 – Proc. Arbitrary reads & writes n Single word cache Single bit/word Abstract other clusters Imprecise timing

Commercial Applications of Symbolic Model Checking Several Commercial Tools n Difficult training and customer support Most Large Companies Have In-House Versions n n IBM, Lucent, Intel, Motorola, SGI, Fujitsu, Siemens, … Many based on Mc. Millan’s SMV program Requires Sophistication n – 27 – Beyond that of mainstream designers

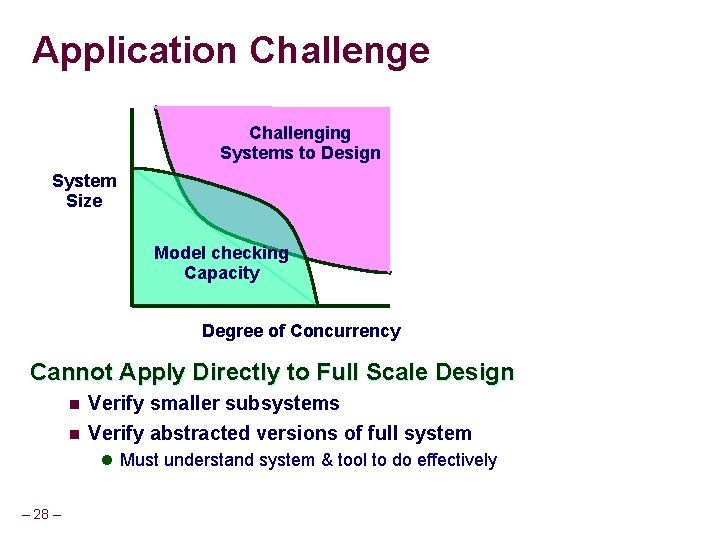
Application Challenge Challenging Systems to Design System Size Model checking Capacity Degree of Concurrency Cannot Apply Directly to Full Scale Design n Verify smaller subsystems n Verify abstracted versions of full system l Must understand system & tool to do effectively – 28 –

Real World Issues Still Too Volatile n Fail by running out of space n Useless once exceed physical memory capacity Ongoing Research to Improve Memory Performance n n Dynamic variable ordering Exploiting modularity of system model l Partitioned transition relations n Exploiting parallelism l Map onto multiple machines l Difficult program for parallel computation » Dynamic, irregular data structures – 29 –

Dynamic Variable Reordering n Richard Rudell, Synopsys Periodically Attempt to Improve Ordering for All BDDs n n Part of garbage collection Move each variable through ordering to find its best location Has Proved Very Successful n n – 30 – Time consuming but effective Especially for sequential circuit analysis

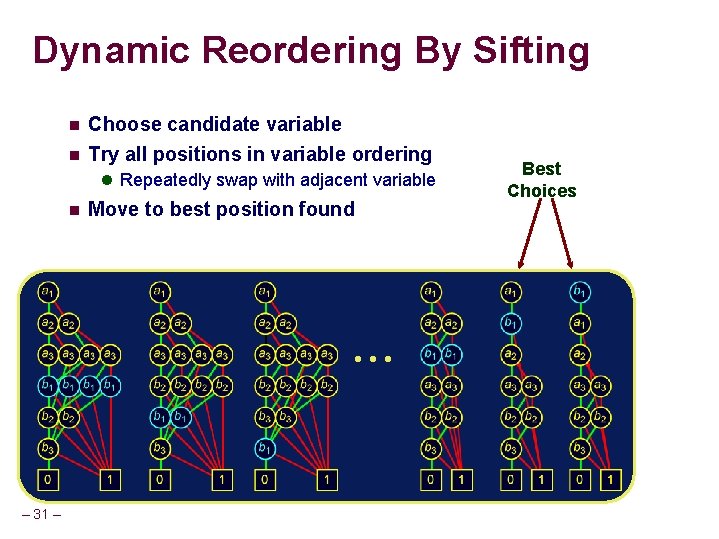
Dynamic Reordering By Sifting n n Choose candidate variable Try all positions in variable ordering l Repeatedly swap with adjacent variable n Move to best position found • • • – 31 – Best Choices

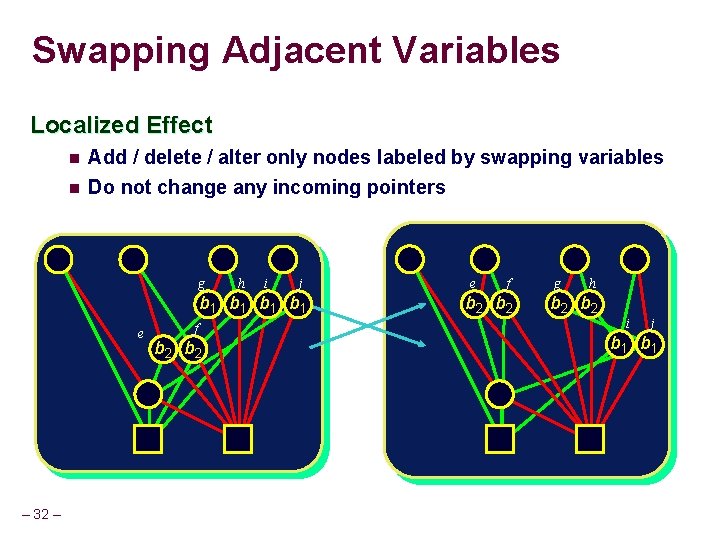
Swapping Adjacent Variables Localized Effect n Add / delete / alter only nodes labeled by swapping variables n Do not change any incoming pointers g h i j b 1 b 1 e – 32 – f b 2 e f b 2 g h b 2 i j b 1

Tuning of BDD Packages Cooperative Effort n n Bwolen Yang, in cooperation with researchers from Colorado, Synopsys, CMU, and T. U. Eindhoven Measure & improve performance of BDDs for symbolic model checking Methodology n n n Generated set of benchmark traces Run 6 different packages on same machine Compare results and share findings l Cooperative competition – 33 –

Effect of Optimizations Compare pre- vs. post-optimized results for 96 runs n 6 different BDD packages n 16 benchmark traces each Limit each run to maximum of 8 CPU hours and 900 MB Measure speedup = Told / Tnew or: n n l New: Failed before but now succeeds l Fail: Fail both times l Bad: Succeeded before, but now fails – 34 –

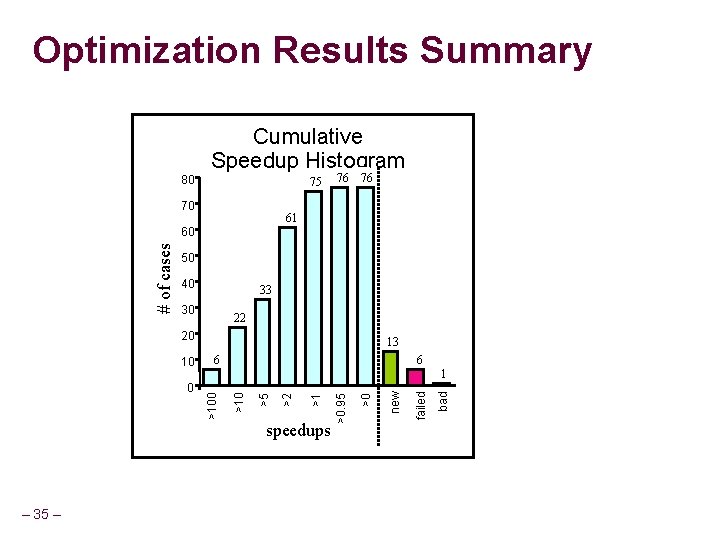
Optimization Results Summary Cumulative Speedup Histogram 80 75 70 76 76 61 50 40 33 30 22 20 6 – 35 – bad >0 failed speedups >0. 95 >1 >2 >5 1 >10 0 6 >100 10 13 new # of cases 60

What’s Good about OBDDs Powerful Operations n Creating, manipulating, testing n Each step polynomial complexity l Graceful degradation Generally Stay Small Enough n n Especially for digital circuit applications Given good choice of variable ordering Weak Competition n n – 36 – No other method comes close in overall strength Especially with quantification operations

Thoughts on Algorithms Research Need to be Willing to Attack Intractable Problems n Many real-world problems NP-hard n No approximations for verification Who Works on These? n Mostly people in application domain l Most work on BDDs in computer-aided design conferences n Not by people with greatest talent in algorithms l No papers in STOC/FOCS/SODA l Probably many ways they could improve things n Fundamental dilemma l Can only make weak formal statements about efficiency l Utility demonstrated empirically – 37 –