Binary bits and bytes At its very lowest

Binary, bits and bytes • At its very lowest level a computer operates by turning on or off millions of tiny switches, called transistors. In computers these transistors can only be in one of two states; that is, on or off. Such devices are thus referred to as two-state devices. Another example of a two-state device might be a conventional light switch. It is either on or off, with no intermediate state. The states of 'on' and 'off' can be represented by the numbers 1 and 0. • In mathematics the term binary is used to refer to a number system which has only two digits, that is 1 and 0. The number system we use in everyday life has ten digits, 0 to 9, and is called denary (decimal). 9/10/2021 Arab. OU - Abu. Nawaf 1

- Binary • The processing units that make up the brains of a computer are simply huge sets of on-off switches • Each Switch has 2 possible positions: – 0 = off – 1 = on • One on-off switch is called a bit “ 0” or “ 1” • “ 8” on-off switches that work together are called a byte “ 0000” or “ 1001 1100” or “ 1111” 9/10/2021 Arab. OU - Abu. Nawaf 2

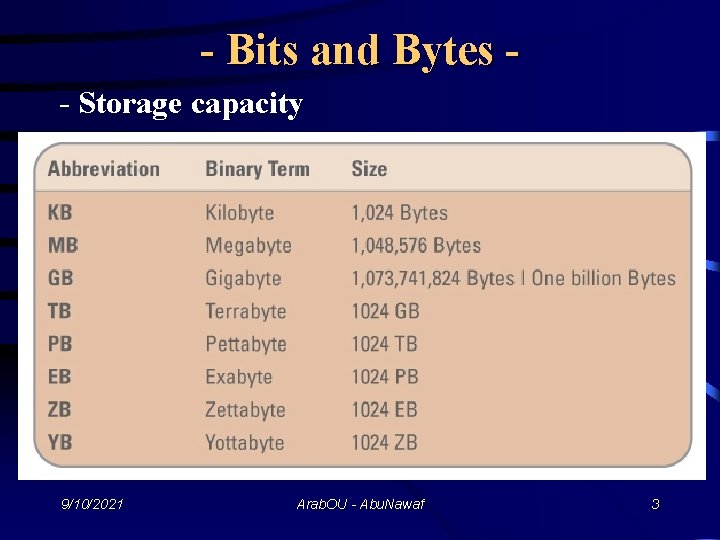
- Bits and Bytes - Storage capacity 9/10/2021 Arab. OU - Abu. Nawaf 3

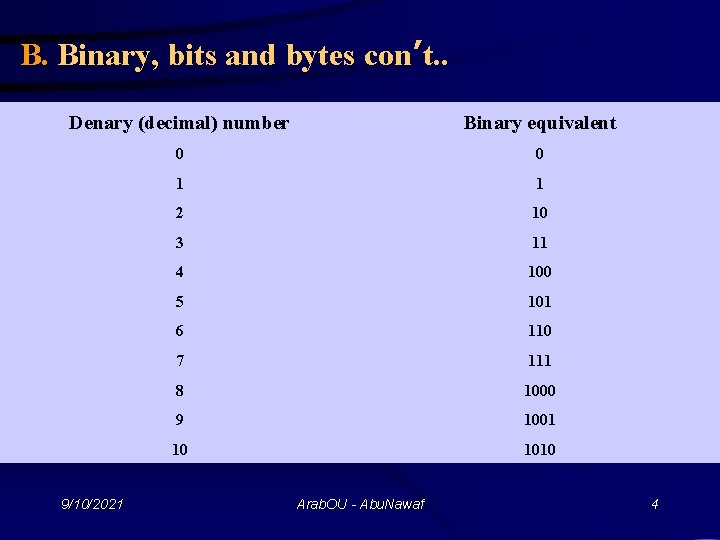
B. Binary, bits and bytes con’t. . Denary (decimal) number Binary equivalent 0 0 1 1 2 10 3 11 4 100 5 101 6 110 7 111 8 1000 9 1001 10 1010 9/10/2021 Arab. OU - Abu. Nawaf 4

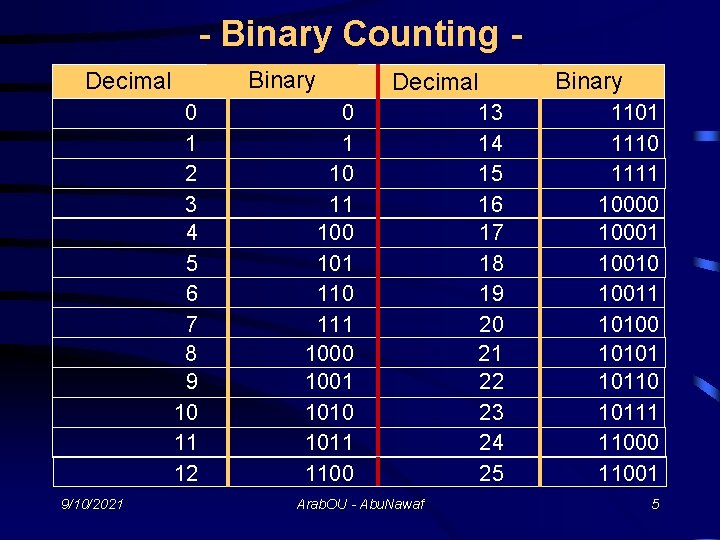
- Binary Counting Binary Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 9/10/2021 Decimal 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 Arab. OU - Abu. Nawaf 13 14 15 16 17 18 19 20 21 22 23 24 25 Binary 1101 1110 1111 10000 10001 10010 10011 10100 10101 10110 10111 11000 11001 5

Decimal to Binary Conversion Convert the decimal number “ 192” into a binary #. 192/2 = 96 with a remainder of 0 96/2 = 48 with a remainder of 0 48/2 = 24 with a remainder of 0 24/2 = 12 with a remainder of 0 12/2 = 6 with a remainder of 0 6/2 = 3 with a remainder of 0 3/2 = 1 with a remainder of 1 1/2 = 0 with a remainder of 1 Write down all the remainders, backwards, and you have the binary number “ 11000000”. 9/10/2021 Arab. OU - Abu. Nawaf 6

Binary to Decimal Conversion From right to left, write the values of the powers of “ 2” above each binary number. Then add up the values where a “ 1” exist. Convert “ 10110101” 27 128 1 26 64 0 25 32 1 24 16 1 23 8 0 22 4 1 21 2 0 20 1 1 128 + 32 + 16 + 4 + 1 = 181 9/10/2021 Arab. OU - Abu. Nawaf 7