Binary Arithmetic Management Information Systems MIS K S

Binary Arithmetic Management Information Systems (MIS) K. S. School of Business Management Samit Tibrewala

Floating Points on Computers �Floating Point Representation: • M is the fraction mantissa. • E is the exponent. • B is the base (Decimal: B=10; Binary: B=2) �Examples: -123. 45 x 10 -6, -3. 45 x 10 -2

Floating Points on Computers �Floating Points on Computers: � S = Sign (0=positive, 1=negative) � E = Exponent (Bias to be adjusted) � M = Mantissa � -3. 154 x 105 � S=1 � E=5 � M = 3. 154 � 32. 12 x 1012 � S=0 � E = 12 � M = 32. 12

Fixed length representations of numbers �Useful in understanding how computers store numbers �Requires conversions from real-world numbers (e. g. HEX – BIN, DEC – BIN, OCT – BIN) �Structured rules

The 8 -bit Conversion Algorithm � STEP 1: If the original number is in hex, convert it to binary. � STEP 2: Separate into the sign, exponent, and mantissa fields. � STEP 3: Extract the mantissa from the mantissa field, and restore the leading one. You may also omit the trailing zeros. � STEP 4: Extract the exponent from the exponent field, and subtract the bias to recover the actual exponent of two. As before, the bias is 2 k− 1 − 1, where k is the number of bits in the exponent field, giving 3 for the 8 -bit format. � STEP 5: De-normalize the number: move the binary point so the exponent is 0, and the value of the number remains unchanged. � STEP 6: Convert the binary value to decimal. This is done just as with binary integers, but the place values right of the binary point are fractions. � STEP 7: Set the sign of the decimal number according to the sign bit of the original floating point number: make it negative for 1; leave positive for 0.

Let’s see ACTUALLY how to do it! Convert the 8 -bit floating point number e 7 (in hex) to decimal. 1. Convert: e 716 = 111001112. 2. Separate: 1 | 110 | 0111 3. Mantissa: 1. 0111 4. Exponent: 1102 = 610; 6 − 3 = 3. 5. De-normalize: 1. 01112 × 23 = 1011. 1

Let’s see ACTUALLY how to do it! Convert the 8 -bit floating point number e 7 (in hex) to decimal. 6. Convert: Exponents 23 22 21 20 2 -1 Place Values 8 4 2 1 0. 5 Bits 1 0 1 1 1 Value 8 0 2 1 0. 5 7. Value = 8 + 0 + 2 + 1 + 0. 5 = 11. 5 8. Sign: Negative 9. RESULT: e 7 is -11. 5

Another one? Convert the 8 -bit floating point number 26 (in hex) to decimal. 1. Convert: 2616 = 001001102. 2. Separate: 0 | 0110 3. Mantissa: 1. 011 4. Exponent: 0102 = 210; 2 − 3 = -1. 5. De-normalize: 1. 0112 × 2 -1 = 0. 1011

Another one? Convert the 8 -bit floating point number 26 (in hex) to decimal. 6. Convert: Exponents 20 2 -1 2 -2 2 -3 Place Values 1 0. 5 0. 25 0. 125 0. 0625 Bits 0 1 Value 0 0. 5 0 0. 125 0. 0625 7. Value = 0. 5 + 0. 125 + 0. 0625= 0. 6875 8. Sign: Positive 9. RESULT: 26 is 0. 6875 2 -4 1

One last round! Convert the 8 -bit floating point number d 3 (in hex) to decimal. 1. Convert: d 316 = 110100112. 2. Separate: 1 | 101 | 0011 3. Mantissa: 1. 0011 4. Exponent: 1012 = 510; 5 − 3 = 2. 5. De-normalize: 1. 00112 × 22 = 100. 11

One last round! Convert the 8 -bit floating point number d 3 (in hex) to decimal. 6. Convert: Exponents 22 21 20 2 -1 2 -2 Place Values 4 2 1 0. 5 0. 25 Bits 1 0 0 1 1 Value 4 0 0 0. 5 0. 25 7. Value = 4 + 0. 5 + 0. 25= 4. 75 8. Sign: Negative 9. RESULT: d 3 is -4. 75

The 8 -bit Conversion Algorithm The other way round (Decimal to Floating Point Binary / Hex) � STEP 1: Convert the absolute value of the number to binary, perhaps with a fractional part after the binary point. This can be done by converting the integral and fractional parts separately. The integral part is converted with the techniques examined previously. The fractional part can be converted by multiplication. This is basically the inverse of the division method: we repeatedly multiply by 2, and harvest each one bit as it appears left of the decimal. � STEP 2: Append × 20 to the end of the binary number (which does not change its value). � STEP 3: Normalize the number. Move the binary point so that it is one bit from the left. Adjust the exponent of two so that the value does not change. � STEP 4: Place the mantissa into the mantissa field of the number. Omit the leading one, and fill with zeros on the right. � STEP 5: Add the bias to the exponent of two, and place it in the exponent field. The bias is 2 k− 1 − 1, where k is the number of bits in the exponent field. For the eight-bit format, k = 3, so the bias is 23− 1 = 3. � STEP 6: Set the sign bit, 1 for negative, 0 for positive, according to the sign of the original number.

Let’s see this one now… Convert 2. 625 to our 8 -bit floating point format 1. Integral Part: 210 = 102. 2. Fractional Part: 0. 625 x 2 = 1. 25 … 1 0. 25 x 2 = 0. 5 … 0 0. 5 x 2 = 1. 0 … 1 3. Therefore, 0. 62510 = 0. 1012 and 2. 62510 = 10. 1012 4. Add the Exponent: 10. 1012 = 10. 1012 × 20 5. Normalize: 10. 1012 × 20 = 1. 01012 × 21

Let’s see this one now… Convert 2. 625 to our 8 -bit floating point format 6. We now have: 1. 01012 × 21 (Normalized form) 7. Mantissa: 0101 8. Exponent: 1 + 3 = 4 = 1002 9. Sign: Positive => 0 10. RESULT: 0 | 100 | 0101

One more… Convert -4. 75 to our 8 -bit floating point format 1. Integral Part: 410 = 1002 2. Fractional Part: 0. 75 x 2 = 1. 5 … 1 0. 5 x 2 = 1. 0 … 1 3. Therefore, 0. 7510 = 0. 112 and 4. 7510 = 100. 112 4. Add the Exponent: 100. 112 = 100. 112 × 20 5. Normalize: 100. 112 × 20 = 1. 00112 × 22

One more… Convert -4. 75 to our 8 -bit floating point format 6. We now have: 1. 00112 × 22 (Normalized form) 7. Mantissa: 0011 8. Exponent: 2 + 3 = 5 = 1012 9. Sign: Negative => 1 10. RESULT: 1 | 101 | 0011

How about this? Convert decimal 1. 7 to our 8 -bit floating point format 1. Integral Part: 110 = 12 2. Fractional Part: 0. 7 x 2 = 1. 4 … 1 0. 4 x 2 = 0. 8 … 0 0. 8 x 2 = 1. 6 … 1 0. 6 x 2 = 1. 2 … 1 0. 2 x 2 = 0. 4 … 0 0. 4 x 2 = 0. 8 … 0 0. 8 x 2 = 1. 6 … 1 0. 6 x 2 = 1. 2 … 1 …… 3. We cannot represent this number as a true floating point number

How about this? Convert decimal 1. 7 to our 8 -bit floating point format 4. The closest we can come in 4 bits (mantissa) is. 1011 5. Since we already have a leading 1, the closest 8 -bit number is 1. 1011 6. This is already normalized => 1. 1011 x 20 7. Exponent: 0 + 3 = 0112 8. Sign: Positive => 0 9. RESULT: 0 | 011 | 1011

Negation of binary numbers �Signed Magnitude �One’s complement �Two’s complement

Signed Magnitude �The left-most bit is not actually a part of the number, but just indicated the +ve / -ve sign. � 0: positive, 1: negative � 12 => 00001100 (1 x 23) + (1 x 22) �-12 => 10001100

1’s Complement �Positive Numbers: Usual Binary � 12 => 00001100 �Negative numbers are represented differently � Replace all zeroes with ones and ones with zeroes (Flip bits) � 12 = 00001100 => -12 = 11110011 �Leftmost bit still indicates the sign

2’s Complement �Begin with the number in 1’s complement � 12 => 00001100 � -12 => 11110011 �Add 1 if the number is negative � -12 => 11110011 + 1 = 11110100

Addition of Binary Numbers �Basic Rules: � 0 + 1 = 1 � 1 + 0 = 1 � 0 + 0 = 0 � 1 + 1 = 0 (Carry: 1)

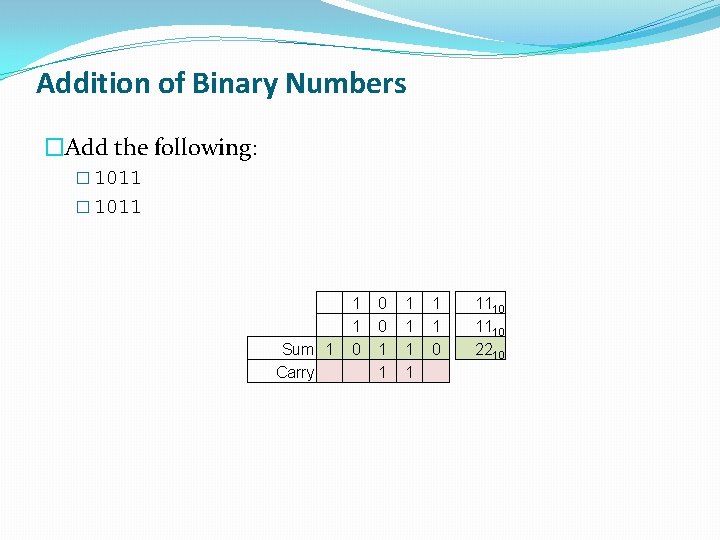
Addition of Binary Numbers �Add the following: � 1011 Sum 1 Carry 1 1 0 0 0 1 1 1 1 0 1110 2210

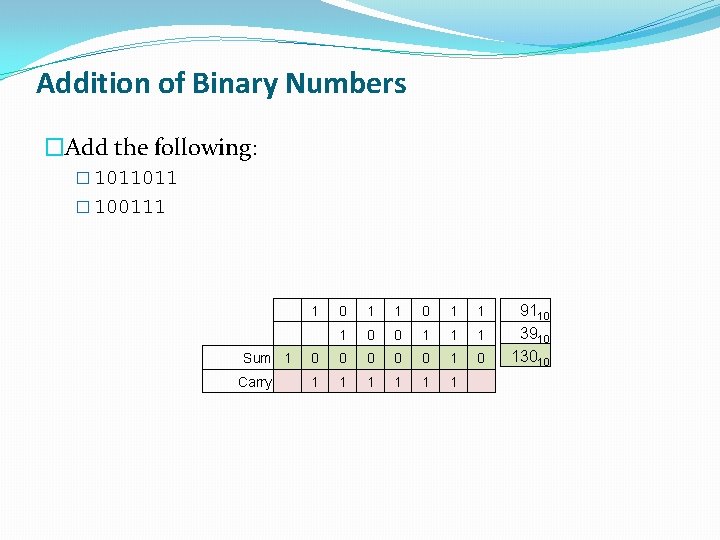
Addition of Binary Numbers �Add the following: � 1011011 � 100111 1 0 1 1 1 0 0 1 1 1 Sum 1 0 0 0 1 0 Carry 1 1 1 9110 3910 13010

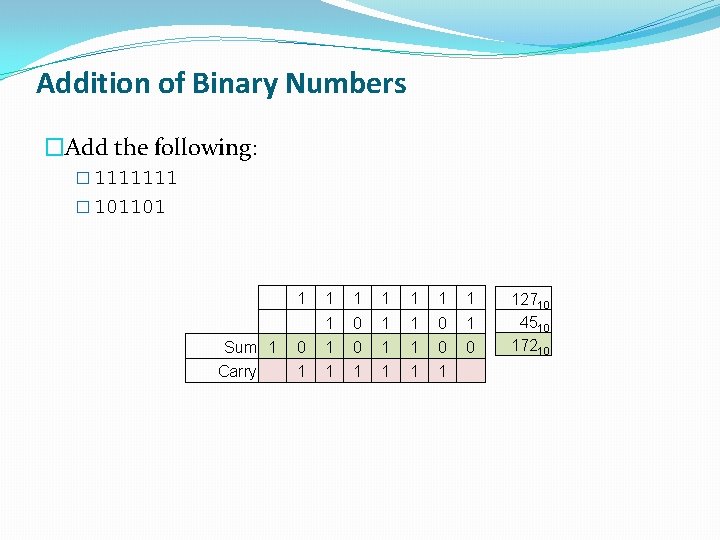
Addition of Binary Numbers �Add the following: � 1111111 � 101101 1 1 1 1 0 1 Sum 1 0 1 1 0 0 Carry 1 1 1 12710 4510 17210

Subtraction of Binary Numbers �Key things to remember: � A – B = A + (-B) � Step 1: Ensure A and B have the same number of bits � Step 2: 1’s Complement of B � Step 3: Add 1 to B � Result at end of Step 3: (-B) � Step 4: Add A and (-B) � Step 5: Discard the last carry digit

Subtraction of Binary Numbers � Calculate: A - B � A = 11101011 � B = 1100110 � Step 1: Same number of bits: � B = 0110 � Step 2: 1’s complement of B � 0110 => 1001 � Step 3: Add 1 � 1001 => 10011010 …(-B)

Subtraction of Binary Numbers � Step 4: Add (A) + (-B): � A = 11101011 � -B = 10011010 � Sum = 110000101 � Step 5: Discard the leading 1 � 110000101 => 10000101 � Let’s confirm: � A = 11101011 = 23510 � B = 1100110 = 10210 � A-B = 10000101 = 13310

Subtraction – Practice! � Calculate: A - B � A = 11000 � B = 1000 � Step 1: Same number of bits: � B = 01000 � Step 2: 1’s complement of B � 01000 => 10111 � Step 3: Add 1 � 10111 => 11000 …(-B)

Subtraction – Practice! � Step 4: Add (A) + (-B): � A = 11000 � -B = 11000 � Sum = 110000 � Step 5: Discard the leading 1 � 110000 => 10000 � Let’s confirm: � A = 11000 = 2410 � B = 1000 = 810 � A-B = 10000 = 1610

Subtraction – Practice! � Calculate: A - B � A = 1100 � B = 101110 � Step 1: Same number of bits: � B = 00101110 � Step 2: 1’s complement of B � 00101110 => 11010001 � Step 3: Add 1 � 11010001 => 11010010 …(-B)

Subtraction – Practice! � Step 4: Add (A) + (-B): � A = 1100 � -B = 11010010 � Sum = 110011110 � Step 5: Discard the leading 1 � 110011110 => 10011110 � Let’s confirm: � A = 1100 = 20410 � B = 101110 = 4610 � A-B = 10011110 = 15810

Subtraction of Binary Numbers Lower minus Higher (negative results) �Key things to remember: � When a higher number is subtracted from a smaller number, the result is negative (e. g. 120 – 132 = -12) � Step 1: Ensure same number of bits � Step 2: Apply 2’s complement to the larger number � Step 3: Add this value to the smaller number � Step 4: Change the sign bit (MSB) to 0 � Step 5: Apply 2’s complement to the value to get your result � Step 6: The MSB will indicate the negative value

Subtraction (Lower – Higher) � Calculate: A - B � A = 1000 � B = 111000 � Step 1: Same number of bits (8 -bit): � A = 00001000 � Step 2: 2’s complement of B � 00111000 => 11000111 + 1 => 11001000 � Step 3: Add the value to smaller number � 11001000 + 00001000 => 11010000

Subtraction (Lower – Higher) � Step 4: Change MSB to 0 � 11010000 => MSB = 1 � MSB=0 => 01010000 � Step 5: Apply 2’s complement � 01010000 => 10101111 + 1 => 10110000 � Step 6: Separate out the MSB � 10110000 => 1 0110000 (MSB=1. . Negative) � Let’s confirm: � A = 1000 = 810 � B = 111000 = 5610 � A-B = 1 0110000 = -4810

Subtraction (Lower – Higher) – Practice! � Calculate: A - B � A = 10010101 � B = 10110100 � Step 1: Same number of bits (8 -bit): � A = 10010101 (Already same) � Step 2: 2’s complement of B � 10110100 => 01001011 + 1 => 01001100 � Step 3: Add the value to smaller number � 01001100 + 10010101 => 11100001

Subtraction (Lower – Higher) – Practice! � Step 4: Change MSB to 0 � 11100001 => MSB = 1 � MSB=0 => 01100001 � Step 5: Apply 2’s complement � 01100001 => 10011110 + 1 => 10011111 � Step 6: Separate out the MSB � 10011111 => 1 0011111(MSB=1. . Negative) � Let’s confirm: � A = 10010101 = 14910 � B = 10110100 = 18010 � A-B = 1 0011111 = -3110

Subtraction (Lower – Higher) – Practice! � Calculate: A - B � A = 10100 � B = 1001001 � Step 1: Same number of bits (8 -bit): � A = 00010100 � Step 2: 2’s complement of B � 01001001 => 10110110 + 1 => 10110111 � Step 3: Add the value to smaller number � 10110111 + 00010100 => 11001011

Subtraction (Lower – Higher) – Practice! � Step 4: Change MSB to 0 � 11001011 => MSB = 1 � MSB=0 => 01001011 � Step 5: Apply 2’s complement � 01001011 => 10110100 + 1 => 10110101 � Step 6: Separate out the MSB � 10110101 => 1 0110101(MSB=1. . Negative) � Let’s confirm: � A = 10100 = 2010 � B = 1001001 = 7310 � A-B = 1 0110101 = -5310

Multiplying Binary Numbers �Key things to remember: � Pretty similar to how we multiple decimal numbers (Phew !) � Long Multiplication Method Multiplying each digit in turn � Adding the values together � � 1*1 = 1 � 1*0 = 0 � 0*1 = 0 � 0*0 = 0

Multiplication – Introduction � Calculate: A * B Let’s confirm: � A = 1011 � B = 111 1011 x 111 ----101100 1011 ------1001101 = SUM 1111 = CARRY A = 1011 = 1110 B = 111 = 710 A*B = 1001101 = 7710

Multiplication – Practice! � Calculate: A * B � A = 10011 Let’s confirm: � B = 1010 10011 x 1010 ----10011000 100110 ----10111110 = SUM - = CARRY A = 10011 = 1910 B = 1010 A*B = 10111110 = 19010

Multiplication – Practice! � Calculate: A * B � A = 1101010 � B = 1101 Let’s confirm: A = 1101010 = 10610 B = 1101 = 1310 A*B = 10101100010 = 137810 1101010 x 1101 ----1101010000 1101010 -----10101100010 = SUM 111111 = CARRY

Dividing Binary Numbers �Key things to remember: � Pretty similar to how we divide decimal numbers (Yippeee!) � Long Division Method � Caution: Take care of Subtractions using “borrowing”

Division – Introduction � Calculate: A / B � A = 1001 � B = 11 1 1 0 1 0 1 1 0 0 0 1 - Let’s confirm: 0 1 1 1 0 0 A = 1001 = 910 B = 11 = 310 A/B = 11 = 310

Division – Practice! � Calculate: A / B � A = 1000010 � B = 110 1 1 0 0 1 1 0 0 0 1 1 0 1 1 1 0 0 0 0 1 1 1 0 Let’s confirm: 1 0 1 0 0 0 A = 1000010 = 6610 B = 110 = 610 A/B = 1011 = 1110

Division – Practice! � Calculate: A / B � A = 1111 � B = 10 1 0 0 1 1 1 1 1 0 1 1 - . . 1 0 Let’s confirm: 1 0 1 1 - 1 0 1 0 0 0 A = 1111 = 1510 B = 10 = 210 A/B = 111. 1 = 7. 510

That’s Binary for you!