Binary and Logic Computers use electrical signals that

Binary and Logic Computers use electrical signals that are on or off, so they have to see everything as a series of binary numbers. This data is represented as a sequence of 1 s and 0 s (on or off). All data that we want a computer to process needs to be converted in to this binary format. Watch Video – What are binary numbers.

Binary Basics Binary is a number system with base 2. Only 2 digits (0 and 1) are used to write every number. This is the foundation of almost every computer program.

Binary Basics Binary to denary (base 10) Each number in binary represents a power of 2, the same way each number in base 10 represents a power of 10. For instance – take the number 1357 1000 s 10 s 1 s 1 3 5 7 This gives us – (1*1000) + (3*100) + (5*10) + (7*1) = 1357

Binary Basics Binary to denary (base 10) The same applies for binary (base 2) but with powers of 2 For instance – take the number 10010101 128 64 32 16 8 4 2 1 1 0 0 1 0 1 Looking only at where the ones are – this gives us: (1*128)+(1*16)+(1*4)+(1*1) or 128+16+4+1 = 149

Binary Basics Binary to denary (base 10) 128 64 32 16 8 4 2 1 1 0 0 1 0 1 Each binary digit above is called a bit. There are 8 bits in the example above. 8 Bits are also called a byte. 4 Bits are called a nibble. Two nibbles make a byte.

Binary Basics Task 1 Complete Binary worksheet 1

Binary Basics Task 2 Write out 10 of your own binary numbers to solve. Use any where from a nibble to a byte. Give these to someone else to convert then check to see if they have got the right answers.

Binary Basics Denary to Binary There are many ways of doing this. Here we will show you a couple of methods Method 1 Take the number and divide it by 2 and show the remainder. For instance – 130 Sum Result Remainder 130 / 2 65 0

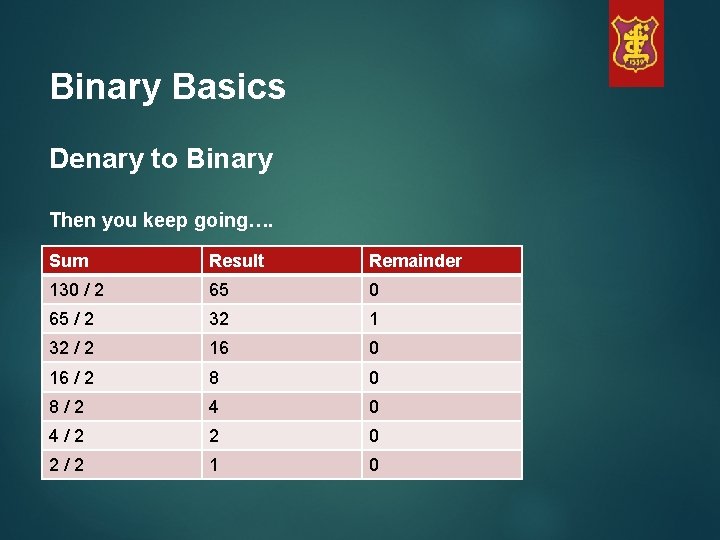
Binary Basics Denary to Binary Then you keep going…. Sum Result Remainder 130 / 2 65 0 65 / 2 32 1 32 / 2 16 0 16 / 2 8 0 8/2 4 0 4/2 2 0 2/2 1 0

Binary Basics Denary to Binary You should always be left with 1. Starting with that read back up the remainder column to give your answer. Sum Result Remainder 130 / 2 65 0 65 / 2 32 1 32 / 2 16 0 16 / 2 8 0 8/2 4 0 4/2 2 0 2/2 1 0 10000010

Binary Basics Denary to Binary 10000010 Lets test to see if it works 128 64 32 16 8 4 2 1 1 0 0 0 1 0 = 128 + 2 = 130 So this method works fine.

Binary Basics Task 3 Using Method 1 Convert the following numbers into binary. 1) 2) 3) 4) 5) 75 127 56 100 24

Binary Basics Denary to Binary Method 2 Here we just keep subtracting the powers of 2 until we have nothing left. For instance let us look at the number 196 – 128 = 68 so we can put a 1 in the 128 position 128 1 64 32 16 8 4 2 1

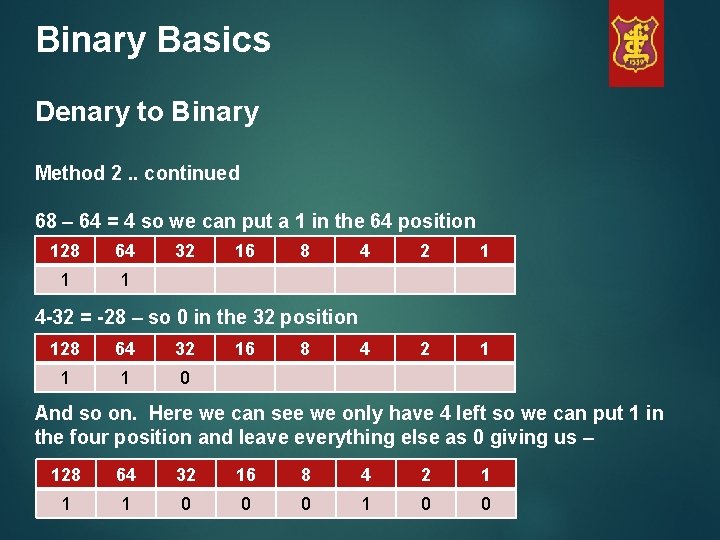
Binary Basics Denary to Binary Method 2. . continued 68 – 64 = 4 so we can put a 1 in the 64 position 128 64 1 1 32 16 8 4 2 1 4 -32 = -28 – so 0 in the 32 position 128 64 32 1 1 0 16 8 And so on. Here we can see we only have 4 left so we can put 1 in the four position and leave everything else as 0 giving us – 128 64 32 16 8 4 2 1 1 1 0 0 0 1 0 0

Binary Basics Denary to Binary Method 2. . continued To confirm that then. . 128 64 32 16 8 4 2 1 1 1 0 0 0 128 + 64 + 4 = 196

Binary Basics Task 4 Using Method 2 Convert the following numbers into binary using 8 bits (byte) 1) 2) 3) 4) 5) 204 177 25 244 89

Binary Basics Task 5 Have a go at Binary Worksheet 2

Binary Basics Task 6 Have a go of the following game. http: //forums. cisco. com/Cert. Com/game/binary_ga me_page. htm

Binary Basics Task 7 Have a look at the following page and try out the questions http: //www. mathsisfun. com/binary-numbersystem. html

Binary Basics Task 8 Have a go at the following game. http: //britton. disted. camosun. bc. ca/binary. swf