Binary AdderSubtractor 1 KU College of Engineering Elec
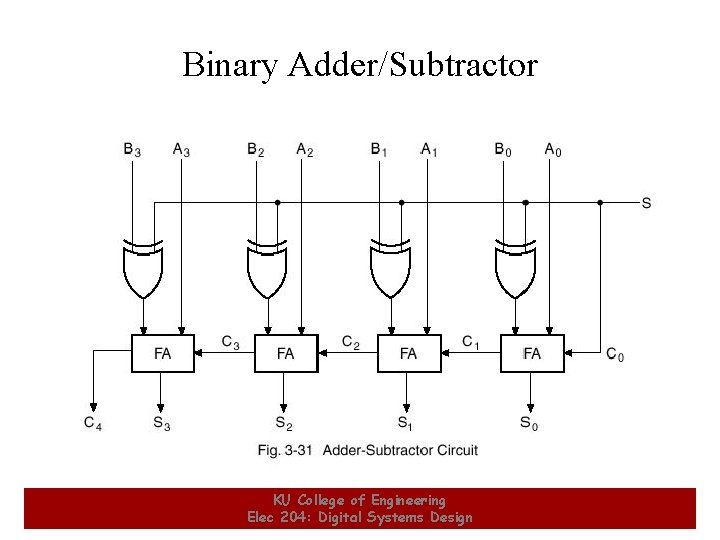
Binary Adder/Subtractor 1 KU College of Engineering Elec 204: Digital Systems Design 1
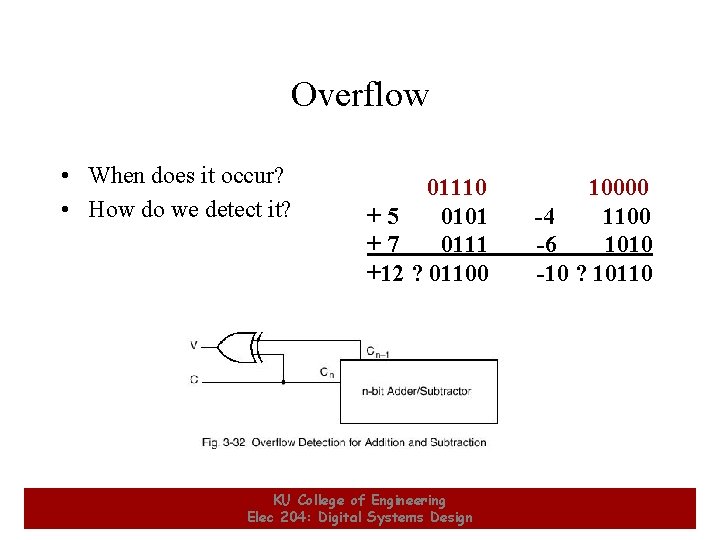
Overflow • When does it occur? • How do we detect it? 2 01110 +5 0101 +7 0111 +12 ? 01100 KU College of Engineering Elec 204: Digital Systems Design 10000 -4 1100 -6 1010 -10 ? 10110 2

Binary Multiplication • The binary digit multiplication table is trivial: (a × b) b=0 b=1 a=0 0 0 a=1 0 1 • This is simply the Boolean AND function. • Form larger products the same way we form larger products in base 10. 3 KU College of Engineering Elec 204: Digital Systems Design 3

Review - Decimal Example: (237 × 149)10 • Partial products are: 237 × 9, 237 × 40, and 237 × 100 • Note that the partial product 2 3 7 summation for n digit, base 10 × 1 4 9 numbers requires adding up to 2 1 3 3 n digits (with carries). 9 4 8 • Note also n × m digit multiply generates up + 2 3 7 - -to an m + n digit result. 3 4 KU College of Engineering Elec 204: Digital Systems Design 5 3 1 3 4

Example: (101 x 011) Base 2 • Partial products are: 101 × 1, 101 × 10, and 101 × 000 • Note that the partial product 1 0 1 summation for n digit, base 2 numbers requires adding up × 0 1 1 to n digits (with carries) in 1 0 1 a column. 1 0 1 • Note also n × m digit 0 0 0 multiply generates up to an m + n digit result 0 0 1 1 (same as decimal). 5 KU College of Engineering Elec 204: Digital Systems Design 5

Multiplier Boolean Equations • We can also make an n × m “block” multiplier and use that to form partial products. • Example: 2 × 2 – The logic equations for each partialproduct binary digit are shown below: • We need to "add" the columns to get the product bits P 0, P 1, P 2, and P 3. b 1 b 0 • Note that some a 1 a 0 columns may ´ generate carries. (a 0. b 1) (a 0. b 0) + (a 1. b 1) (a 1. b 0) P 3 P 2 P 1 P 0 6 KU College of Engineering Elec 204: Digital Systems Design 6
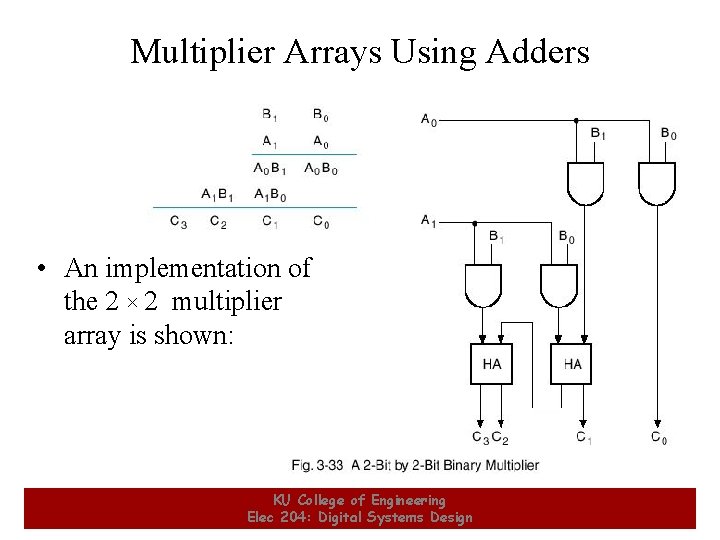
Multiplier Arrays Using Adders • An implementation of the 2 × 2 multiplier array is shown: 7 KU College of Engineering Elec 204: Digital Systems Design 7

4 -bit by 3 -bit multiplier 8 KU College of Engineering Elec 204: Digital Systems Design 8

Design by Contraction • Contraction is a technique for simplifying the logic in a functional block to implement a different function – The new function must be realizable from the original function by applying rudimentary functions to its inputs – Contraction is treated here only for application of 0 s and 1 s (not for X and X’) – After application of 0 s and 1 s, equations or the logic diagram are simplified 9 KU College of Engineering Elec 204: Digital Systems Design 9
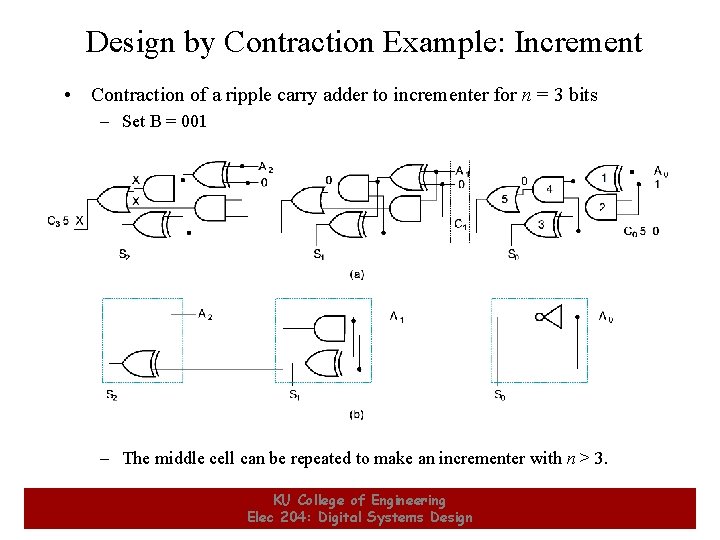
Design by Contraction Example: Increment • Contraction of a ripple carry adder to incrementer for n = 3 bits – Set B = 001 – The middle cell can be repeated to make an incrementer with n > 3. 10 KU College of Engineering Elec 204: Digital Systems Design 10

Incrementing & Decrementing • Incrementing – – Adding a fixed value to an arithmetic variable Fixed value is often 1, called counting (up) Examples: A + 1, B + 4 Functional block is called incrementer • Decrementing – – 11 Subtracting a fixed value from an arithmetic variable Fixed value is often 1, called counting (down) Examples: A - 1, B - 4 Functional block is called decrementer KU College of Engineering Elec 204: Digital Systems Design 11
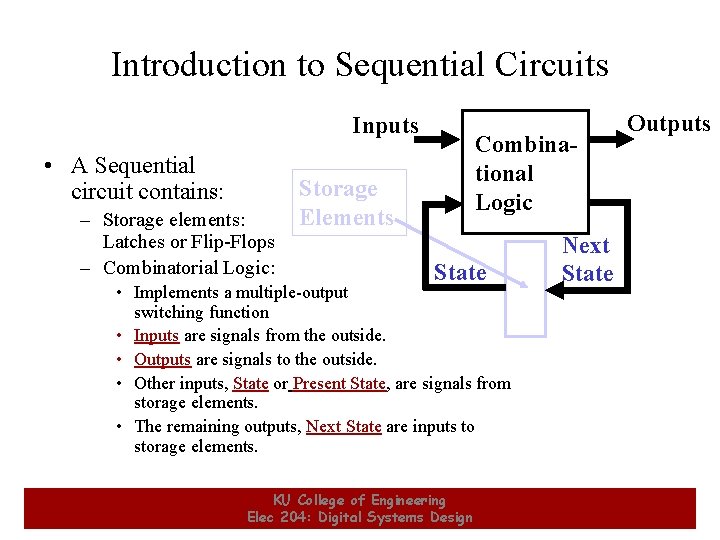
Introduction to Sequential Circuits Inputs • A Sequential circuit contains: – Storage elements: Latches or Flip-Flops – Combinatorial Logic: Combinational Logic Storage Elements State • Implements a multiple-output switching function • Inputs are signals from the outside. • Outputs are signals to the outside. • Other inputs, State or Present State, are signals from storage elements. • The remaining outputs, Next State are inputs to storage elements. 12 KU College of Engineering Elec 204: Digital Systems Design Outputs Next State 12
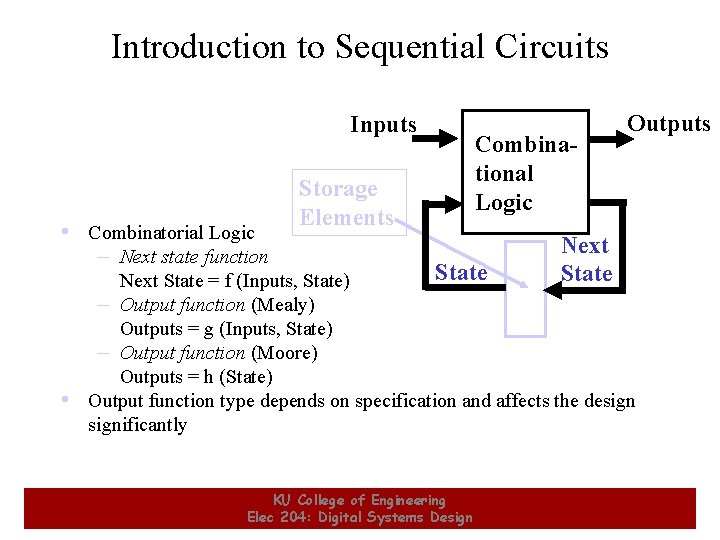
Introduction to Sequential Circuits Inputs • Combinatorial Logic – Next state function Storage Elements Combinational Logic Outputs Next State = f (Inputs, State) – Output function (Mealy) Outputs = g (Inputs, State) – Output function (Moore) Outputs = h (State) • Output function type depends on specification and affects the designificantly 13 KU College of Engineering Elec 204: Digital Systems Design 13

Types of Sequential Circuits • Depends on the times at which: – storage elements observe their inputs, and – storage elements change their state • Synchronous – Behavior defined from knowledge of its signals at discrete instances of time – Storage elements observe inputs and can change state only in relation to a timing signal (clock pulses from a clock) • Asynchronous – Behavior defined from knowledge of inputs an any instant of time and the order in continuous time in which inputs change – If clock just regarded as another input, all circuits are asynchronous! – Nevertheless, the synchronous abstraction makes complex designs tractable! 14 KU College of Engineering Elec 204: Digital Systems Design 14

Discrete Event Simulation • In order to understand the time behavior of a sequential circuit we use discrete event simulation. • Rules: – Gates modeled by an ideal (instantaneous) function and a fixed gate delay – Any change in input values is evaluated to see if it causes a change in output value – Changes in output values are scheduled for the fixed gate delay after the input change – At the time for a scheduled output change, the output value is changed along with any inputs it drives 15 KU College of Engineering Elec 204: Digital Systems Design 15

Simulated NAND Gate • Example: A 2 -Input NAND gate with a 0. 5 ns. delay: F(Instantaneous) A DELAY 0. 5 ns. F B • Assume A and B have been 1 for a long time • At time t=0, A changes to a 0 at t= 0. 8 ns, back to 1. t (ns) A B – 1 1 0 1Þ 0 1 0. 5 0. 8 1Ü 0 1 0. 13 16 1 1 F(I) 0 1Ü 0 F Comment 0 A=B=1 for a long time 0 F(I) changes to 1 1Ü 0 F changes to 1 after a 0. 5 ns delay 1 F(Instantaneous) changes to 0 1Þ 0 F changes to 0 after a 0. 5 ns delay KU College of Engineering Elec 204: Digital Systems Design 16

Gate Delay Models • Suppose gates with delay n ns are represented for n = 0. 2 ns, n = 0. 4 ns, n = 0. 5 ns, respectively: 0. 2 17 0. 4 KU College of Engineering Elec 204: Digital Systems Design 0. 5 17
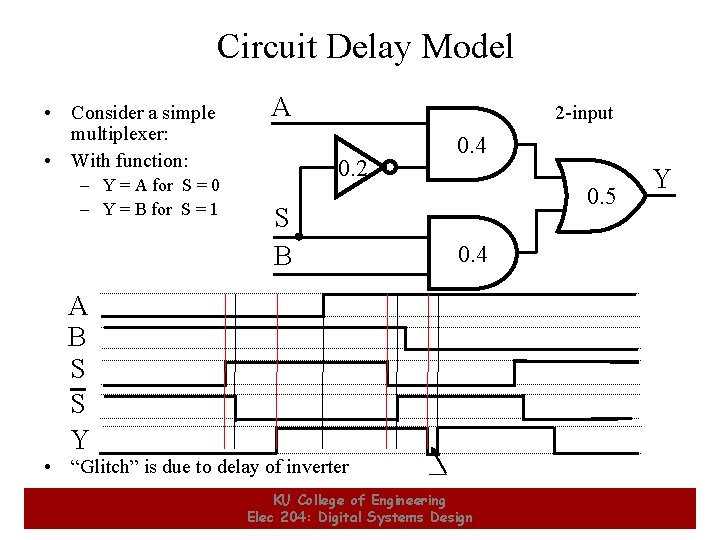
Circuit Delay Model • Consider a simple multiplexer: • With function: – Y = A for S = 0 – Y = B for S = 1 A 2 -input 0. 2 S B 0. 4 0. 5 Y 0. 4 A B S S Y • “Glitch” is due to delay of inverter 18 KU College of Engineering Elec 204: Digital Systems Design 18
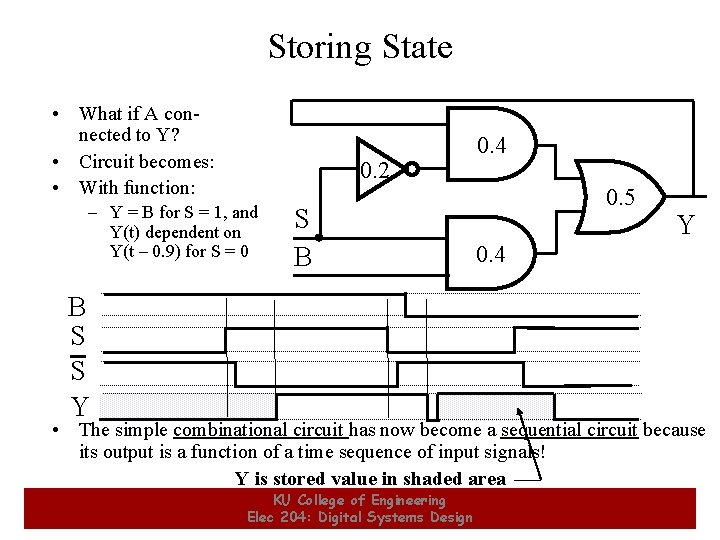
Storing State • What if A connected to Y? • Circuit becomes: • With function: – Y = B for S = 1, and Y(t) dependent on Y(t – 0. 9) for S = 0 B S S Y 0. 2 S B 0. 4 0. 5 Y 0. 4 • The simple combinational circuit has now become a sequential circuit because its output is a function of a time sequence of input signals! Y is stored value in shaded area KU College of Engineering 19 19 Elec 204: Digital Systems Design

Storing State (Continued) • Simulation example as input signals change with time. Changes occur every 100 ns, so that the tenths of ns delays are negligible. Time B 1 1 1 0 0 0 1 S 0 1 0 0 Y 0 1 1 1 0 0 0 Comment Y “remembers” 0 Y = B when S = 1 Now Y “remembers” B = 1 for S = 0 No change in Y when B changes Y = B when S = 1 Y “remembers” B = 0 for S = 0 No change in Y when B changes • Y represent the state of the circuit, not just an output. 20 KU College of Engineering Elec 204: Digital Systems Design 20
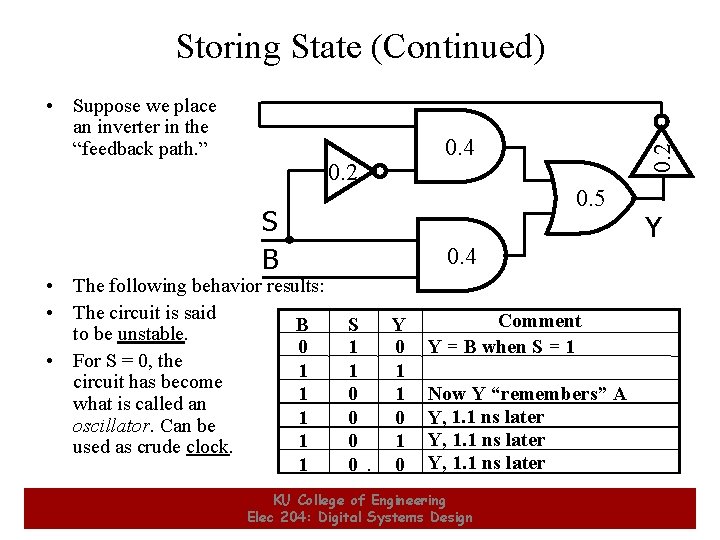
Storing State (Continued) 0. 4 0. 2 0. 5 S B • The following behavior results: • The circuit is said B to be unstable. 0 • For S = 0, the 1 circuit has become 1 what is called an 1 oscillator. Can be 1 used as crude clock. 1 21 0. 2 • Suppose we place an inverter in the “feedback path. ” Y 0. 4 S 1 1 0 0 Y 0 1 1 0 Comment Y = B when S = 1 Now Y “remembers” A Y, 1. 1 ns later KU College of Engineering Elec 204: Digital Systems Design 21
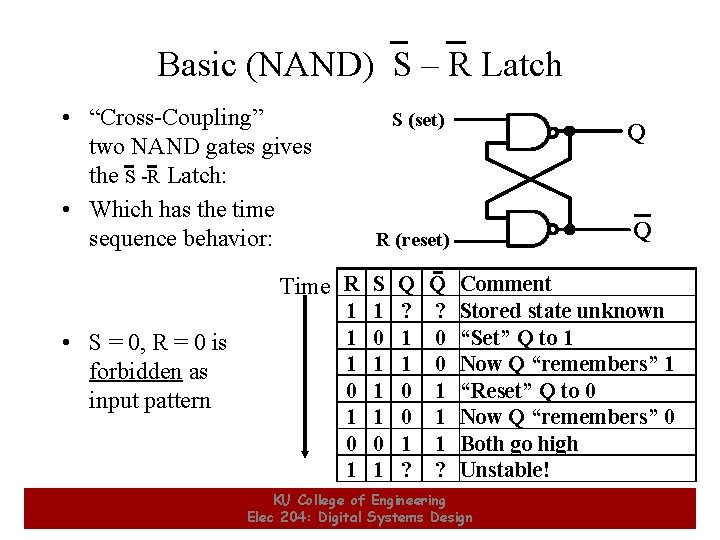
Basic (NAND) S – R Latch • “Cross-Coupling” two NAND gates gives the S -R Latch: • Which has the time sequence behavior: S (set) Q Q R (reset) Time R S Q Q Comment • S = 0, R = 0 is forbidden as input pattern 22 1 1 1 0 1 ? 1 1 0 0 1 ? ? 0 0 1 1 1 ? Stored state unknown “Set” Q to 1 Now Q “remembers” 1 “Reset” Q to 0 Now Q “remembers” 0 Both go high Unstable! KU College of Engineering Elec 204: Digital Systems Design 22

Basic (NOR) S – R Latch • Cross-coupling two NOR gates gives the S – R Latch: • Which has the time sequence behavior: Time R 0 0 0 1 0 23 R (reset) Q Q S (set) S 0 1 0 0 0 1 0 Q ? 1 1 0 0 0 ? Q ? 0 0 1 1 0 ? Comment Stored state unknown “Set” Q to 1 Now Q “remembers” 1 “Reset” Q to 0 Now Q “remembers” 0 Both go low Unstable! KU College of Engineering Elec 204: Digital Systems Design 23
- Slides: 23