Big Oh Sorting and Linked List Intro Data

Big Oh, Sorting, and Linked List Intro Data Structures and Algorithms CS 244 Brent M. Dingle, Ph. D. Department of Mathematics, Statistics, and Computer Science University of Wisconsin – Stout This presentation requires Sound Enabled Based on the book: Data Structures and Algorithms in C++ (Goodrich, Tamassia, Mount) Some content derived/taken from: http: //www. stroustrup. com/Programming/ and some from Data Structures for Game Programmers (Penton)

Things to Note • Homework 6 is Posted on D 2 L – Do NOT delay in starting it • The first graded online quiz starts soon – Plan is to provide time to take it during the NEXT class • After the Test Review • But you can take it anytime until its due date • First Exam is 1 week from today

Notes on Homework • Some comments on Homework 6 follow • Offering clarification on interpretation of a couple questions

Linear Search vs. Binary Search ^ successfully performed

Running Time Comparisons log n here means “log Base 2 of n”

From Last Time • Searching Methods – Linear Search – Binary Search • Big-Oh – Lots of information – Many Examples

For Today • More on Big-Oh – Remember you should now be reading the official book for the class: circa Chapter 4+ • Data Structures & Algorithms in C++, 2 nd Edition – Goodrich, Tamassia, Mount • Some sorting • A quick linked list intro

Marker Slide • Any General Questions ? • Next up – Big-Oh • Some Formulas • Examples – Recursion and Iterative Functions – Insertion Sort – Linked Lists

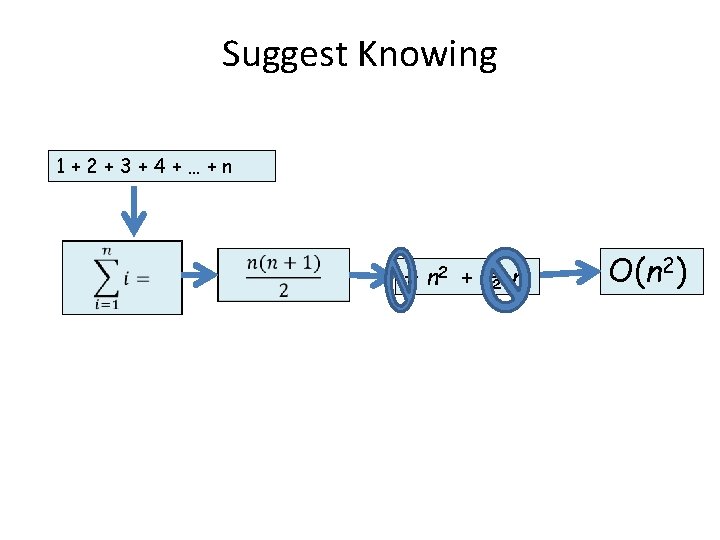
Suggest Knowing 1+2+3+4+…+n ½ n 2 + ½ n O(n 2)

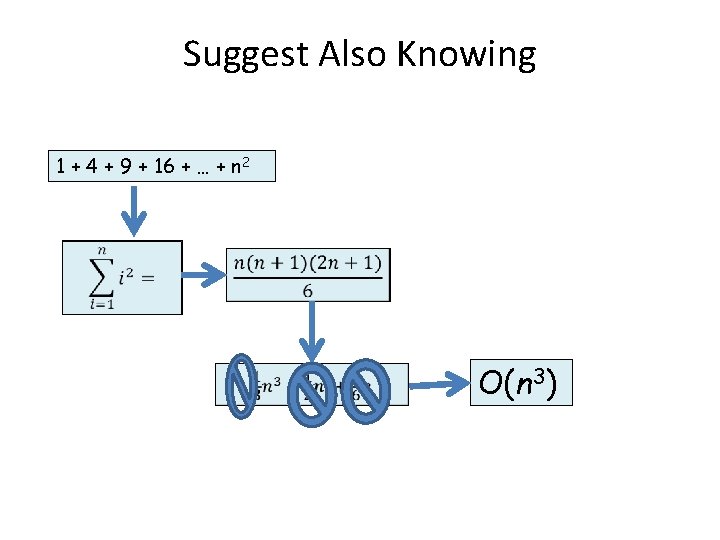
Suggest Also Knowing 1 + 4 + 9 + 16 + … + n 2 O(n 3)

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • Next up – Big-Oh • Examples – Recursion and Iterative Functions – Insertion Sort – Linked Lists

Note: Not all C++ • Some of the following examples – and some in your homework – and some on your quizzes and tests • will NOT be C++ – consider it pseudo-code – with some of it looking a lot like Java • Why? – Because Big-Oh Analysis is NOT C++ specific – It applies to all algorithms implemented in any language

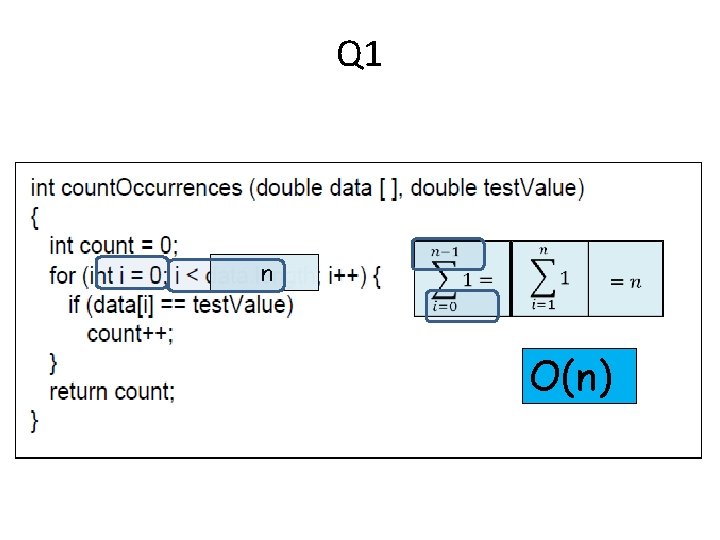
Q 1 n O(n)

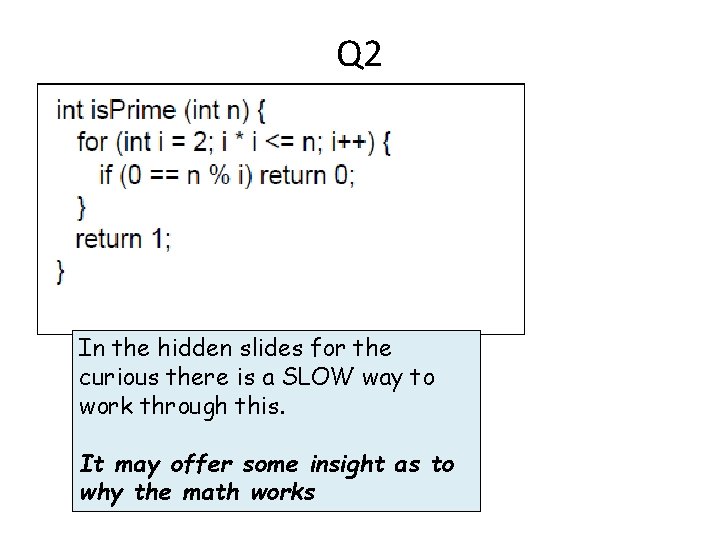
Q 2 In the hidden slides for the curious there is a SLOW way to work through this. It may offer some insight as to why the math works

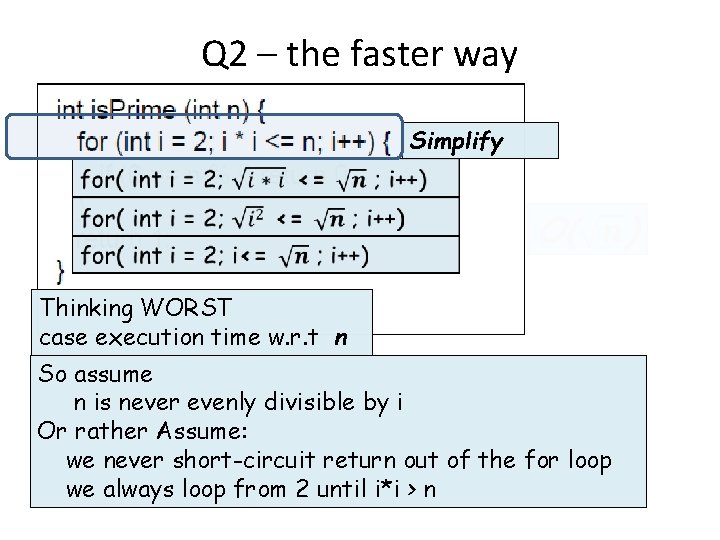
Q 2 – the faster way Simplify Thinking WORST case execution time w. r. t n So assume n is never evenly divisible by i Or rather Assume: we never short-circuit return out of the for loop we always loop from 2 until i*i > n

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • First couple example • Next up – Big-Oh • More Examples – Recursion and Iterative Functions – Insertion Sort – Linked Lists

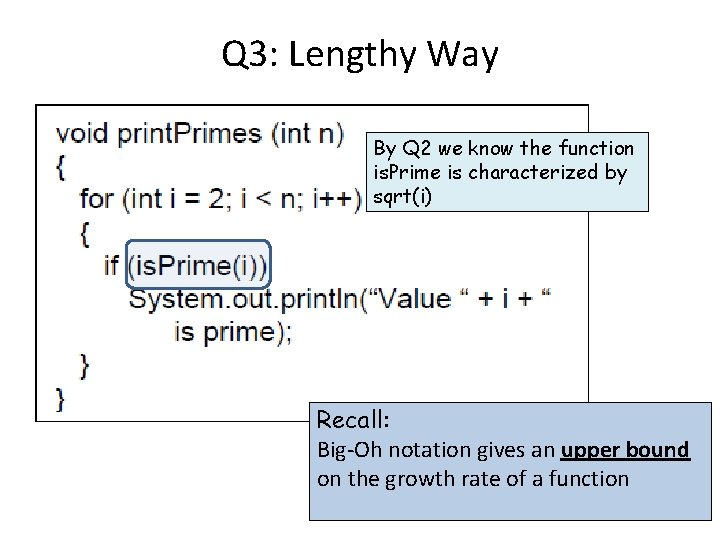
Q 3: Lengthy Way By Q 2 we know the function is. Prime is characterized by sqrt(i) Recall: Big-Oh notation gives an upper bound on the growth rate of a function

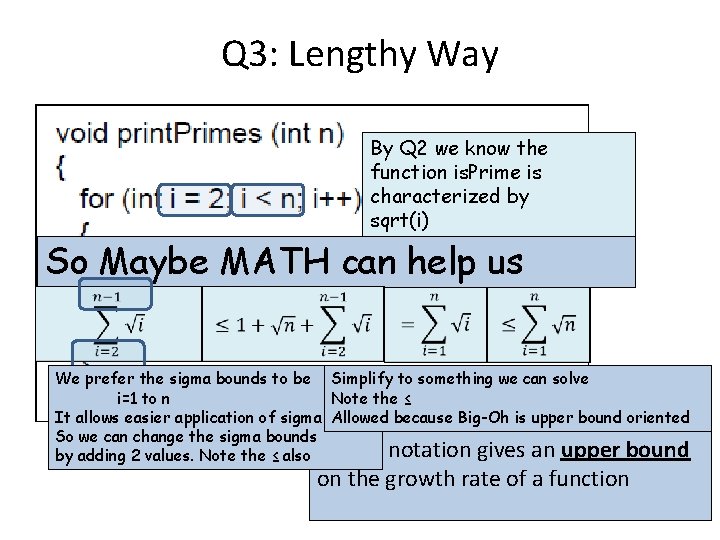
Q 3: Lengthy Way By Q 2 we know the function is. Prime is characterized by sqrt(i) So Maybe MATH can help us We prefer the sigma bounds to be Simplify to something we can solve i=1 to n Note the ≤ It allows easier application of sigma. Recall: rules Allowed because Big-Oh is upper bound oriented So we can change the sigma bounds by adding 2 values. Note the ≤ also Big-Oh notation gives an upper bound on the growth rate of a function

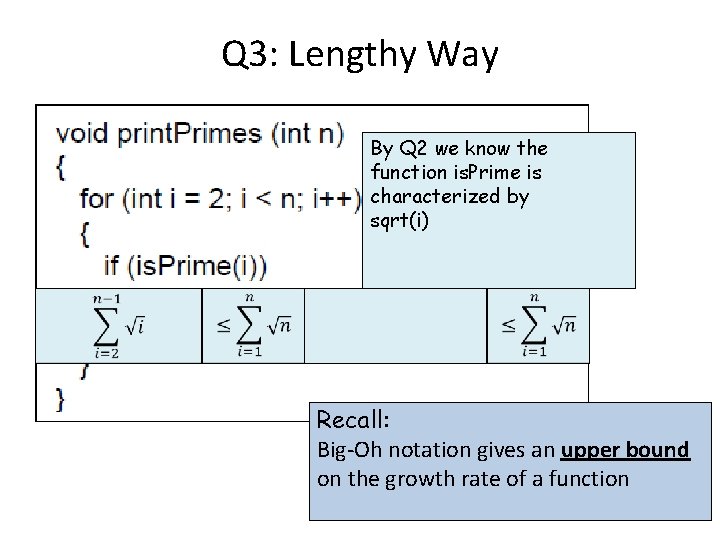
Q 3: Lengthy Way By Q 2 we know the function is. Prime is characterized by sqrt(i) Recall: Big-Oh notation gives an upper bound on the growth rate of a function

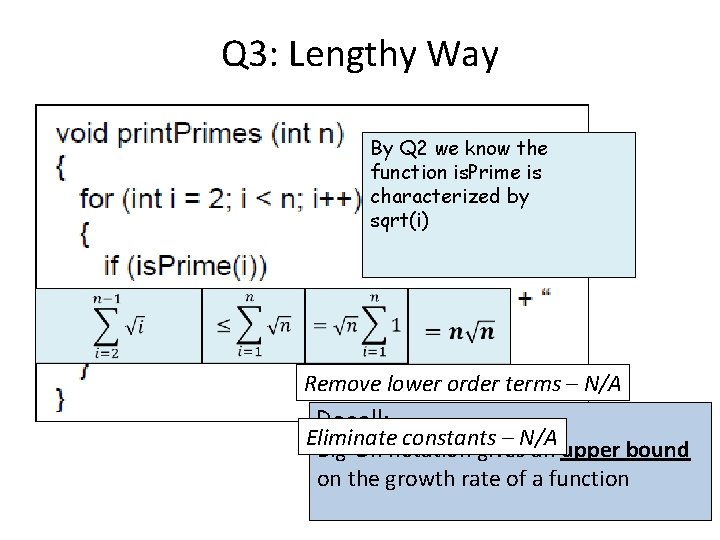
Q 3: Lengthy Way By Q 2 we know the function is. Prime is characterized by sqrt(i) Remove lower order terms – N/A Recall: Eliminate constants – N/A Big-Oh notation gives an upper bound on the growth rate of a function

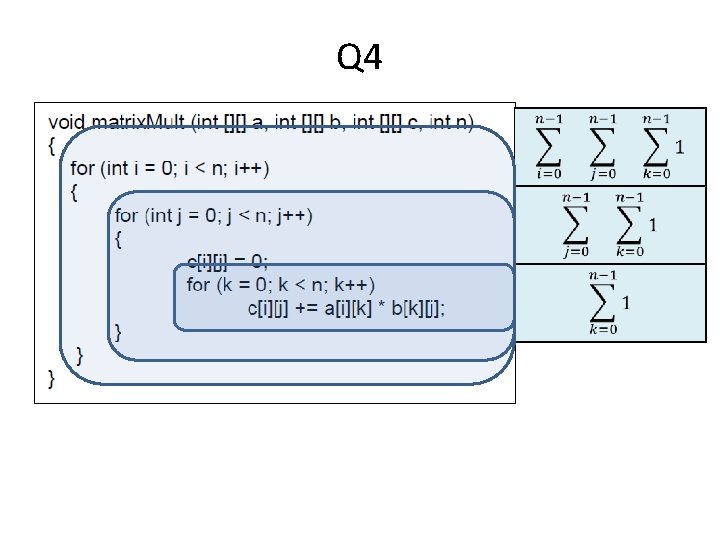
Q 4

Q 4: Lengthy Way Justifies Op Count Way O(n 3) Remove Eliminatelower constants order –terms N/A – N/A

Q 4: Operation Count Operations n

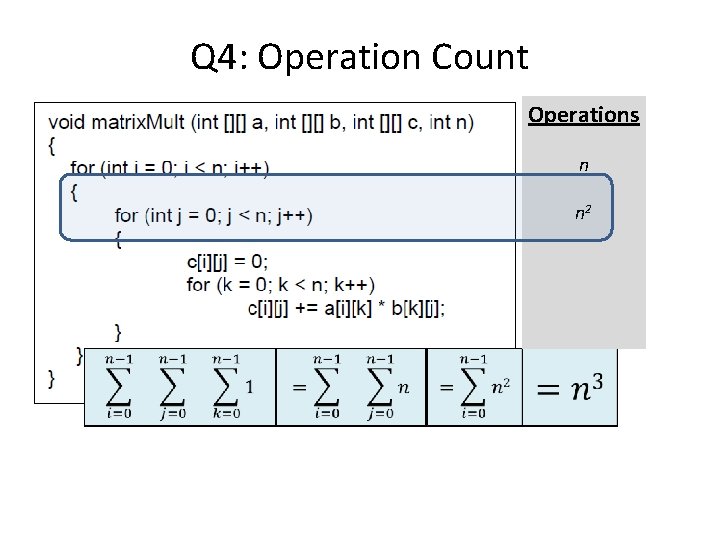
Q 4: Operation Count Operations n n 2

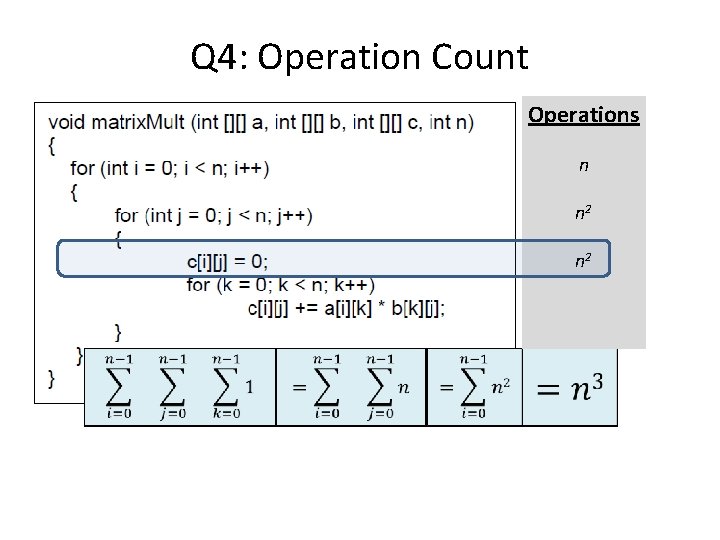
Q 4: Operation Count Operations n n 2

Q 4: Operation Count Operations n n 2 n 3

Q 4: Operation Count Operations n n 2 n 3

Q 4: Operation Count Operations n n 2 O(n 3) n 2 n 3

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • First 4 examples or so • Next up – Big-Oh • More Examples – Recursion and Iterative Functions – Insertion Sort – Linked Lists

So what remains? … Q 5 void selection. Sort(double storage[], int n) { for (int p = n-1; p > 0; p--) for (int i=0; i <= p; i++) Considered Constant Do something taking constant time } Considered Constant

So what remains? … Q 5 void selection. Sort(double storage[], int n) { p = n-1 inner loops runs n times for (int p = n-1; p > 0; p--) p = n-2 inner loops runs n-1 times for (int i=0; i <= p; i++) p = n-3 inner loops runs n-2 times Do something taking p = n-4 inner loops runs n-3 times constant time : : } p = 1 inner loops runs 2 times 2+3+4+…+n = ½ n 2 + ½ n O(n 2) Eliminate Remove lower constants order terms

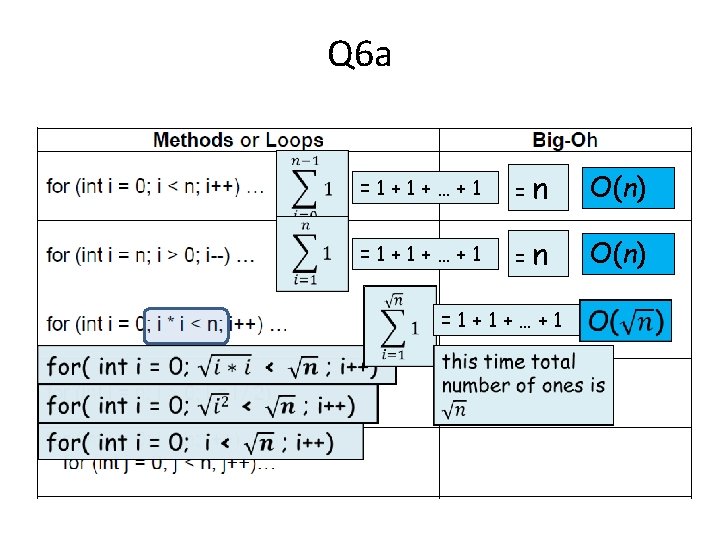
Q 6 a =1+1+…+1 = n O(n) =1+1+…+1

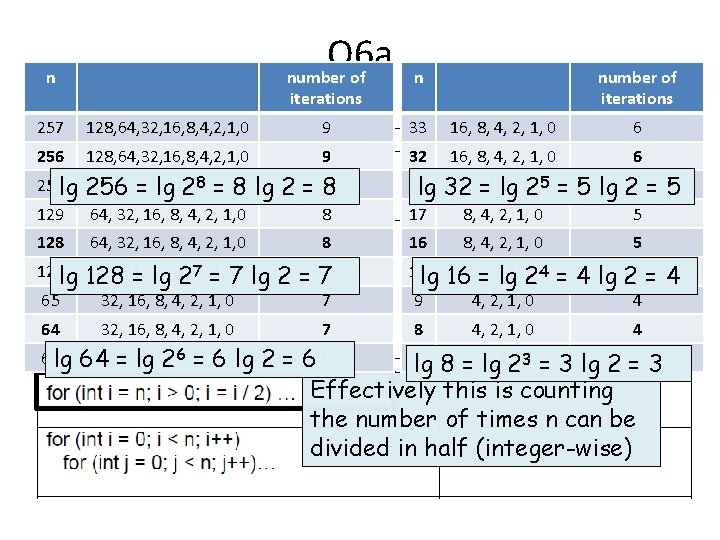
Q 6 a number of n iterations n number of iterations 257 128, 64, 32, 16, 8, 4, 2, 1, 0 9 33 16, 8, 4, 2, 1, 0 6 256 128, 64, 32, 16, 8, 4, 2, 1, 0 9 32 16, 8, 4, 2, 1, 0 6 8, 4, 2, 1, 0 5 8, 4, 2, 1, 0 O(n)4 255 lg 256 127, 63, =31, lg 15, 287, 3, 1, 0 = 8 lg 2 = 88 31 lg 129 64, 32, 16, 8, 4, 2, 1, 0 8 17 128 64, 32, 16, 8, 4, 2, 1, 0 8 16 127 lg 63, 31, 0 lg 2 = 7 7 128 = 15, lg 7, 273, =1, 7 65 64 63 lg 32, 16, 8, 4, 2, 1, 0 7 15 lg 9 8 15, =7, lg 3, 1, 32 205 = 5 O(n) lg 25 = 5 5 0 4 = 4 lg 2 = 4 16 7, =3, lg 1, 2 4, 2, 1, 0 4 15, 2 7, 63, =1, 6 0 lg 2 = 6 6 7 8 = 3, 64 31, = lg lg lg 1, 203 = 3 lg 2 =3 3 Effectively this is counting the number of times n can be divided in half (integer-wise)

We seem to be off by 1 each timenumber with ofthe lgn n n number of So let’s add 1 iterations and characterize this 257 128, 64, 32, 16, 8, 4, 2, 1, 0 9 33 for 16, loop 8, 4, 2, 1, 0 6 by the function 256 128, 64, 32, 16, 8, 4, 2, 1, 0 9 32 16, 8, 4, 2, 1, 0 6 255 lg 256 127, 63, =31, 31 15, =7, lg 3, 1, lg 15, 287, 3, 1, 0 = 8 lg 2 = 88 lg 32 205 = 5 O(n) lg 25 = 5 18 + lg n 17 8, O(lg 129 64, 32, 16, 8, 4, 2, 1, 0 n) 5 Q 6 a 128 64, 32, 16, 8, 4, 2, 1, 0 8 5 Remove lower order terms 16 8, 4, 2, 1, 0 O(n) 127 lg 128 63, 31, 0 lg 2 = 7 7 15 lg 16 7, =3, lg 1, 2 0 4 = 4 lg 24 = 15, lg 7, 273, =1, 7 Eliminate 65 32, 16, 8, 4, 2, 1, 0 constants 7 – N/A 9 4, 2, 1, 0 4 64 32, 16, 8, 4, 2, 1, 0 63 lg 7 15, 2 7, 63, =1, 6 0 lg 2 = 6 6 64 31, = lg 8 4, 2, 1, 0 4 7 8 = 3, lg lg 1, 203 = 3 lg 2 =3 3 O(lg n)

Q 6 a O(n) Remove Eliminatelower constants order –terms N/A – N/A O(lg n) O(n 2)

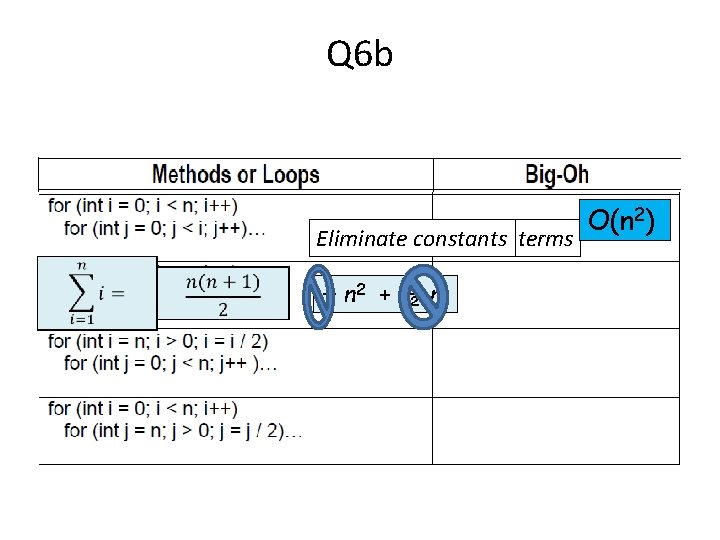
Q 6 b Eliminate Remove lower constants order terms ½ n 2 + ½ n O(n 2)

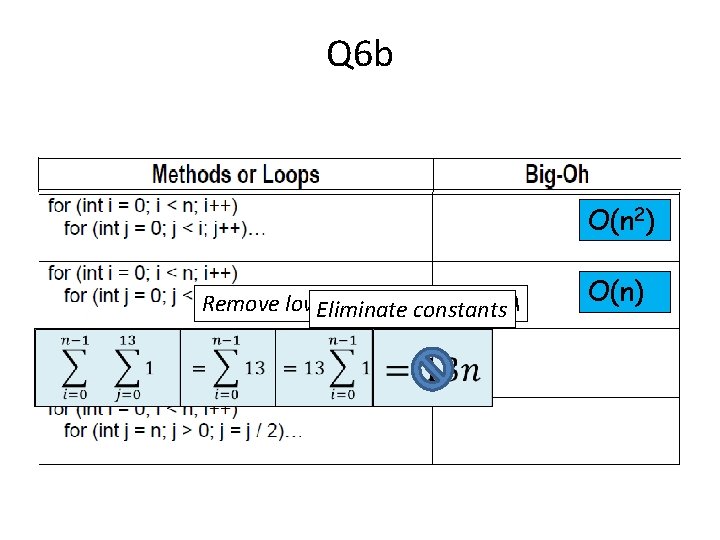
Q 6 b O(n 2) Remove lower order terms – N/A Eliminate constants O(n)

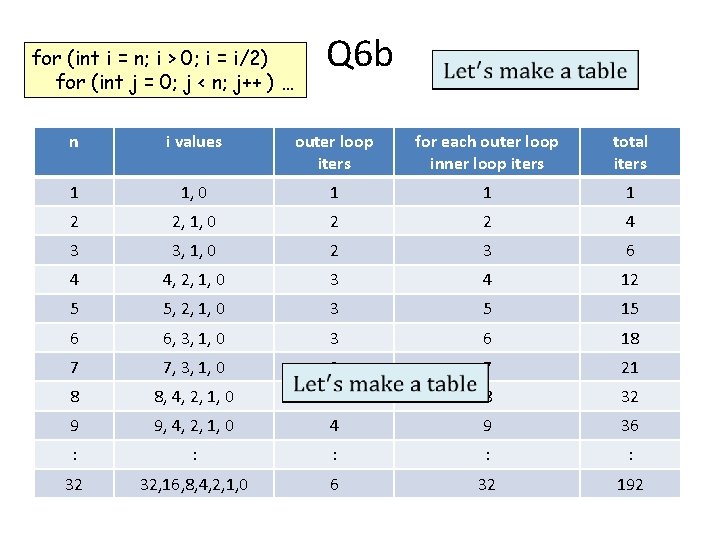
for (int i = n; i > 0; i = i/2) for (int j = 0; j < n; j++ ) … Q 6 b n i values outer loop iters for each outer loop inner loop iters total iters 1 1, 0 1 1 2 2, 1, 0 2 2 3 3, 1, 0 2 3 6 4 4, 2, 1, 0 3 4 12 5 5, 2, 1, 0 3 5 O(n) 15 6 6, 3, 1, 0 3 6 18 7 7, 3, 1, 0 3 7 21 8 8, 4, 2, 1, 0 4 8 32 9 9, 4, 2, 1, 0 4 9 36 : : : 32 32, 16, 8, 4, 2, 1, 0 6 32 192 1 O(n 42)

for (int i = n; i > 0; i = i/2) for (int j = 0; j < n; j++ ) … Q 6 b And this is just n for eachseen outer loop total We’ve this before inner loop iters it was ( 1 + lg n ) iters n i values outer loop iters 1 1, 0 1 2 2, 1, 0 2 2 3 3, 1, 0 2 3 6 4 4, 2, 1, 0 3 4 12 5 5, 2, 1, 0 3 5 O(n) 15 6 6, 3, 1, 0 6 7 7, 3, 1, 0 3 n 7 18 8 8, 4, 2, 1, 0 4 8 32 9 9, 4, 2, 1, 0 4 9 36 : : : 32 32, 16, 8, 4, 2, 1, 0 6 32 192 (1 + lg n) 3 1 1 O(n 42) 21

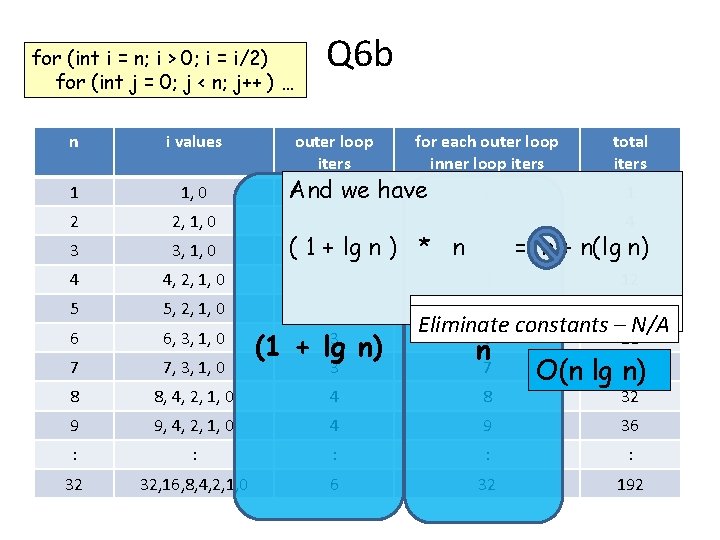
for (int i = n; i > 0; i = i/2) for (int j = 0; j < n; j++ ) … Q 6 b n i values outer loop iters for each outer loop inner loop iters 1 1, 0 2 2, 1, 0 3 3, 1, 0 4 4, 2, 1, 0 3 4 5 5, 2, 1, 0 3 6 6, 3, 1, 0 5 Remove 7 7, 3, 1, 0 8 And 1 we have 2 ( 1 +2 lg n ) * n (1 + lg n) 3 1 2 3 total iters 1 O(n 42) = n + n(lg 6 n) 12 O(n) 15 lower order–terms Eliminate constants N/A 6 18 3 n 7 8, 4, 2, 1, 0 4 8 9 9, 4, 2, 1, 0 4 9 36 : : : 32 32, 16, 8, 4, 2, 1, 0 6 32 192 O(n lg 21 n) 32

Q 6 b O(n 2) O(n) By Similar we arrive at: O(n lg n)

HINTS: Polynomial Classifications

HINTS: Polynomial Classifications = 15 n + 5 n lg n

HINTS: Polynomial Classifications

HINTS: Polynomial Classifications

HINTS: Polynomial Classifications = n 4 + lesser terms

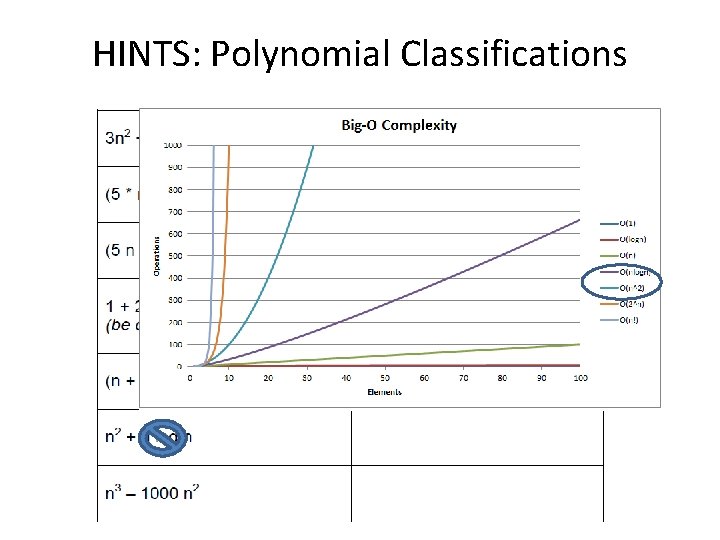
HINTS: Polynomial Classifications

HINTS: Polynomial Classifications

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • Examples • Next up – Recursion and Iterative Functions – Insertion Sort – Linked Lists

Definition of Recursion • See definition of recursion – Error – infinite loop… ARGH!

Recursive Functions • Just a reminder that – Recursive Functions are • Functions that call themselves

Iterative Functions • Also recall it is possible to rewrite recursive functions as iterative functions

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • Examples – Recursion and Iterative Functions • Next up – Insertion Sort – Linked Lists

Sorting • Insertion Sort – Similar to Selection Sort • Selection Sort was mentioned in the homework – Insertion Sort • Also mentioned in Chapter 3 of the textbook

Sorting: Motivation • Sorted data can be more useful than unsorted data – Example: • Binary Search is fast but only works on sorted data • Sorting and Searching – Very common things for computers to do – Been looking for faster ways for a long time • Begin with Insertion Sort – Is a common thing people do for small data sets in the “real world” (not using computers)

Insertion Sort Pseudo-code Algorithm void insertion. Sort(int a[], int size) { int j; for (int p=1; p < size; p++) { int tmp = a[p]; j = p; } } while ( (j > 0) && { a[j] = a[j-1]; --j; } a[j]=tmp; (tmp < a[j-1]) ) a[] could be any type that has a comparison operation defined for it. For example, we can sort strings by alphabetizing them (i. e. we can compare each string using ‘a’ < ‘b’ < ‘c’ … < ‘z’ ) And this may be useful later int main () { std: : string str 1 (“Samuel"); std: : string str 2 (“Henry"); if (str 1. compare(str 2) < 0) { std: : cout << str 1 << " is before “; std: : cout << str 2 << 'n'; } : return 0 }

Insertion Sort: Step Through p =1 j=? tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } ? 15 SORTED 4 13 2 21

Insertion Sort: Step Through p =1 j=? tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 4 15 SORTED 4 13 2 21

Insertion Sort: Step Through p =1 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 4 15 SORTED 4 13 2 21

Insertion Sort: Step Through p =1 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 4 < 15 yes a[j]=tmp; } } 4 15 SORTED 4 13 2 21

Insertion Sort: Step Through p =1 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[1] = a[0] (i. e. a[1] = 15) a[j]=tmp; } } 4 15 SORTED 15 13 2 21

Insertion Sort: Step Through p =1 j=0 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 4 15 SORTED 15 13 2 21

Insertion Sort: Step Through p =1 j=0 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 NO a[j]=tmp; } } 4 15 SORTED 15 13 2 21

Insertion Sort: Step Through p =1 j=0 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; i. e. a[0] = 4 } } 4 4 SORTED 15 13 2 21

Insertion Sort: Step Through p =2 j=? void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } End iteration 1 Begin iteration 2 tmp = ? 4 SORTED 15 13 2 21

Insertion Sort: Step Through p =2 j=? tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } ? 4 SORTED 15 13 2 21

Insertion Sort: Step Through p =2 j=? tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 13 4 SORTED 15 13 2 21

Insertion Sort: Step Through p =2 j=2 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 13 4 SORTED 15 13 2 21

Insertion Sort: Step Through p =2 j=2 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 13 < 15 yes a[j]=tmp; } } 13 4 SORTED 15 13 2 21

Insertion Sort: Step Through p =2 j=2 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[2] = a[1] (i. e. a[2] = 15) a[j]=tmp; } } 13 4 SORTED 15 15 2 21

Insertion Sort: Step Through p =2 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 13 4 SORTED 15 15 2 21

Insertion Sort: Step Through p =2 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 13 < 4 NO a[j]=tmp; } } 13 4 SORTED 15 15 2 21

Insertion Sort: Step Through p =2 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; i. e. a[1] = 13 } } 13 4 SORTED 13 15 2 21

Insertion Sort: Step Through p =3 j=? void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } End iteration 2 Begin iteration 3 tmp = ? 4 SORTED 13 15 2 21

Insertion Sort: Step Through p =3 j=? tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 2 4 SORTED 13 15 2 21

Insertion Sort: Step Through p =3 j=3 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 2 4 SORTED 13 15 2 21

Insertion Sort: Step Through p =3 j=3 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 2 < 15 yes a[j]=tmp; } } 2 4 SORTED 13 15 2 21

Insertion Sort: Step Through p =3 j=3 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[3] = a[2] (i. e. a[3] = 15) a[j]=tmp; } } 2 4 SORTED 13 15 15 21

Insertion Sort: Step Through p =3 j=2 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 2 4 SORTED 13 15 15 21

Insertion Sort: Step Through p =3 j=2 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 2 < 13 yes a[j]=tmp; } } 2 4 SORTED 13 15 15 21

Insertion Sort: Step Through p =3 j=2 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[2] = a[1] i. e. a[2] = 13 a[j]=tmp; } } 2 4 SORTED 13 13 15 21

Insertion Sort: Step Through p =3 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 2 4 SORTED 13 13 15 21

Insertion Sort: Step Through p =3 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 2 < 4 yes a[j]=tmp; } } 2 4 SORTED 13 13 15 21

Insertion Sort: Step Through p =3 j=1 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[1] = a[0] i. e a[1] = 4 a[j]=tmp; } } 2 4 SORTED 4 13 15 21

Insertion Sort: Step Through p =3 j=0 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 2 4 SORTED 4 13 15 21

Insertion Sort: Step Through p =3 j=0 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 NO a[j]=tmp; } } 2 4 SORTED 4 13 15 21

Insertion Sort: Step Through p =3 j=0 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[0] = 2 a[j]=tmp; } } 2 2 SORTED 4 13 15 21

Insertion Sort: Step Through p =4 j=? void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } End iteration 3 Begin iteration 4 tmp = ? 2 SORTED 4 13 15 21

Insertion Sort: Step Through p =4 j=? tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 21 2 SORTED 4 13 15 21

Insertion Sort: Step Through p =4 j=4 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } 21 2 SORTED 4 13 15 21

Insertion Sort: Step Through p =4 j=4 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } j > 0 yes 21 < 15 NO a[j]=tmp; } } 21 2 SORTED 4 13 15 21

Insertion Sort: Step Through p =4 j=4 tmp = void insertion. Sort(int a[], int size) { for (int p=1; p < size; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[4] = 21 a[j]=tmp; } } 21 2 SORTED 4 13 15 21

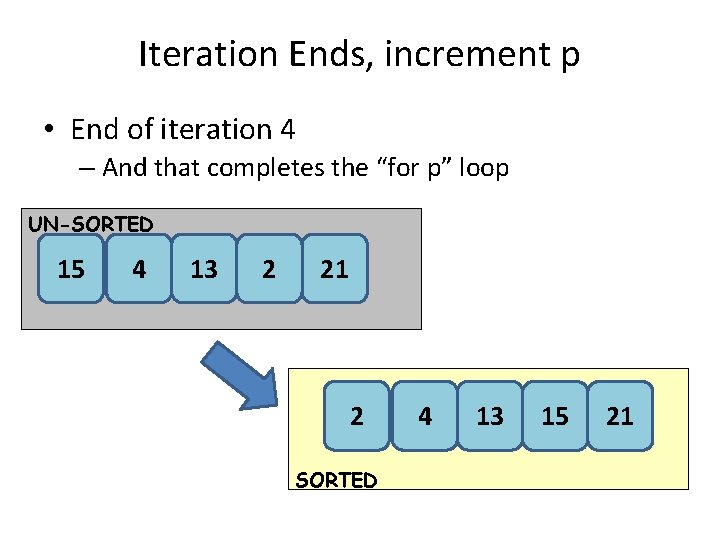
Iteration Ends, increment p • End of iteration 4 – And that completes the “for p” loop UN-SORTED 15 4 13 2 21 2 SORTED 4 13 15 21

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • Examples – Recursion and Iterative Functions – Insertion Sort: Walk-Through • Next up – Insertion Sort: Analysis – Linked Lists

Begin Analysis • We will first review two simple examples of loops – Because insertion sort has two loops too • for loop, do loop makes no difference

Example 1 -loop Analysis void some. Fun(int a[], int { for (int p=1; p <= { n) n; p++) This for-loop executes n times. do something } } How many times do we So we “do something” ? n times

Example 2 -loop Analysis void some. Fun(int a[], int { for (int p=1; p <= { } } n) n; p++) for (int j=1; j <= n; j++) { do something } How many times do we “do something” ? This for-loop executes n times. This for-loop also executes n times.

Begin Application • Having that in our mind • We will now apply Big-Oh analysis methods to Insertion Sort

Application of Analysis to Insertion Sort let’s make n void insertion. Sort(int a[], int size) n be theloop same thing The outer will execute { as size n-1 times for (int p=1; p < nsize; p++) { The inner loop is tricker int tmp = a[p]; It starts at p and goes int j = p; while ( (j > 0) && (tmp < a[j-1]) ) down to zero { a[j] = a[j-1]; And can terminate early. --j; But we want the } a[j]=tmp; WORST case } The one that executes How many times do we } “do something” ? the most number of times

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n The outer loop will execute { n-1 times for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } }

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n { for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } Operations n

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n { for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } Operations n n n

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n { for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } Operations n n 2

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n { for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } Operations n n 2 n 2

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n { for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; --j; } a[j]=tmp; } } Operations n n 2 n 2 n

Application of Analysis to Insertion Sort void insertion. Sort(int a[], int size) n { for (int p=1; p < nsize; p++) { int tmp = a[p]; int j = p; while ( (j > 0) && (tmp < a[j-1]) ) { a[j] = a[j-1]; 2 --j; } a[j]=tmp; } } O(n ) Operations n n 2 n 2 n

Insertion Sort Concludes • So ends Insertion Sort

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • Examples – Recursion and Iterative Functions – Insertion Sort • Next up – Linked Lists

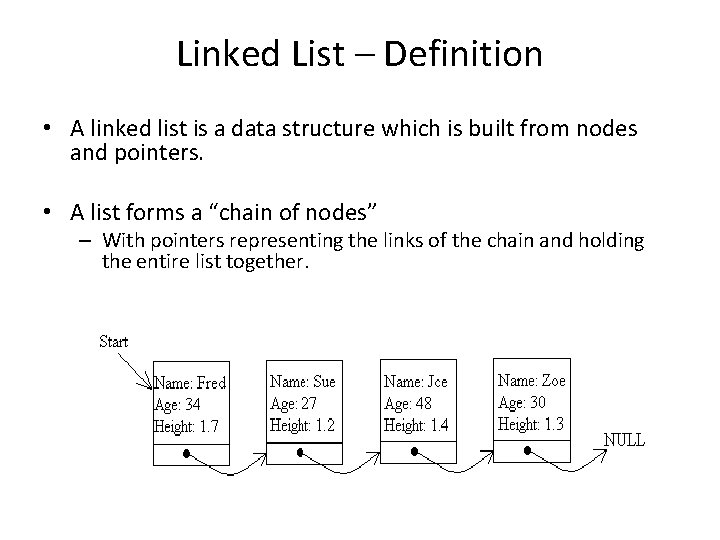
Linked List – Definition • A linked list is a data structure which is built from nodes and pointers. • A list forms a “chain of nodes” – With pointers representing the links of the chain and holding the entire list together.

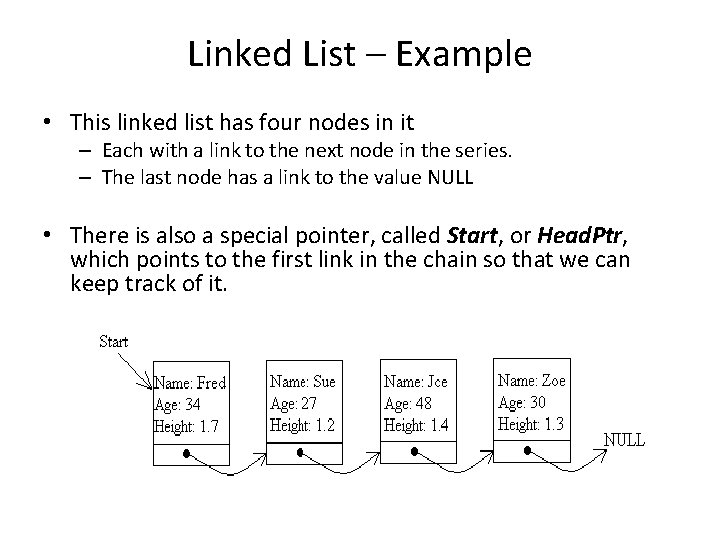
Linked List – Example • This linked list has four nodes in it – Each with a link to the next node in the series. – The last node has a link to the value NULL • There is also a special pointer, called Start, or Head. Ptr, which points to the first link in the chain so that we can keep track of it.

Linked List: The Human Way • We will first investigate the marvelous world of humans • And their uncanny ability to use pointers

What You Need • How to create a list using – Pointers – Nodes

List of One • Have a list of ONE node – The HEAD of the list

Add a Node • The head of the list is set to point at the node to add – Now we have 2 nodes in our list

Add Another Node • The 2 nd node is set to point at the node to add – Now we have 3 nodes in our list – Keep going…

Marker Slide • Any Questions On: – Big-Oh • Some Formulas • Examples – Recursion and Iterative Functions – Insertion Sort – Linked Lists: The Human Way • Next up – Linked Lists: The Computer Way

Linked List – Implementation • Key part of a linked list is the node structure – Which holds the data for each node • name, age, height, pointer to next node class Node { public: string m_name; int m_age; // age in years double m_height; // height in meters Node* mp_next; // pointer to next node Others may }; call start. Ptr start, to keep track Node* start. Ptr = NULL; // global variable head, head. Ptr // of beginning of the list root, root. Ptr

Class Board Work • A library wants to manage its books with a computer program. • A book is characterized by – the author, the title, and the ISBN number • What would a node structure (class) look like Practice and prepare for in this case? questions like these. – Take suggestions from students They make good test/quiz – Implement on the board type questions

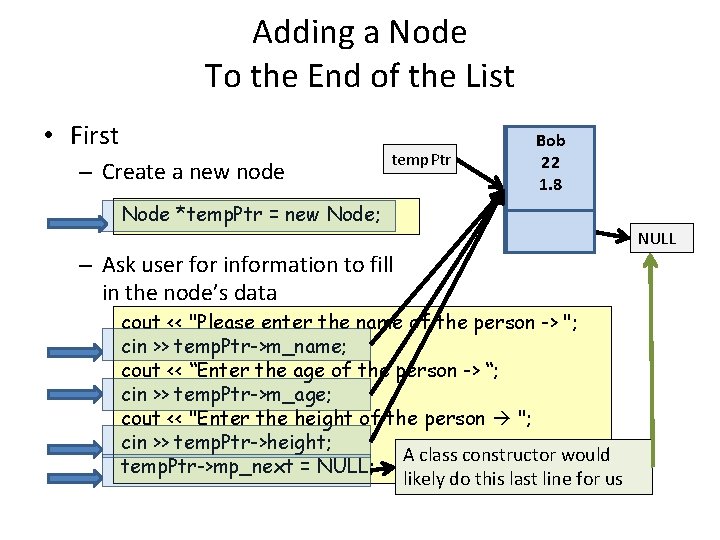
Adding a Node To the End of the List • First – Create a new node temp. Ptr Bob 22 22 1. 8 Node *temp. Ptr = new Node; – Ask user for information to fill in the node’s data cout << "Please enter the name of the person -> "; cin >> temp. Ptr->m_name; cout << “Enter the age of the person -> “; cin >> temp. Ptr->m_age; cout << "Enter the height of the person "; cin >> temp. Ptr->height; A class constructor would temp. Ptr->mp_next = NULL; likely do this last line for us NULL ? ? ?

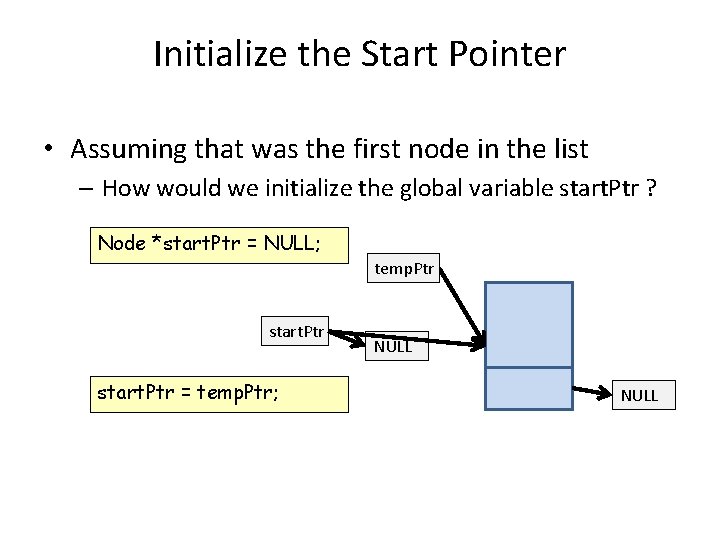
Initialize the Start Pointer • Assuming that was the first node in the list – How would we initialize the global variable start. Ptr ? Node *start. Ptr = NULL; temp. Ptr start. Ptr ? ? ? = temp. Ptr; NULL

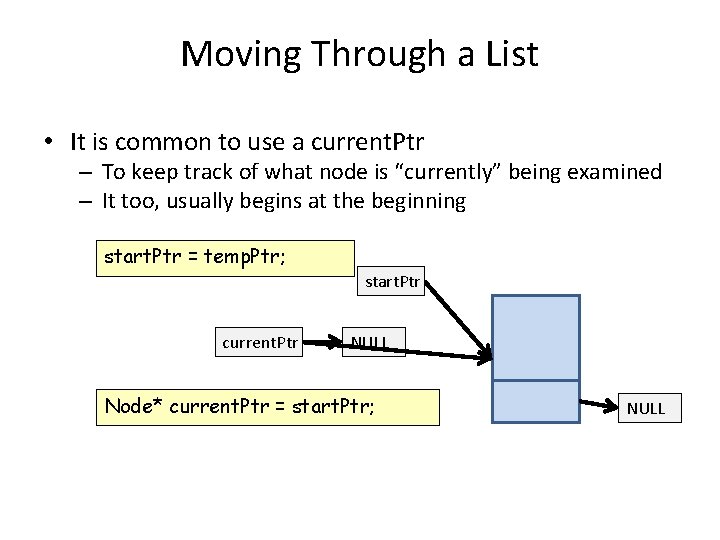
Moving Through a List • It is common to use a current. Ptr – To keep track of what node is “currently” being examined – It too, usually begins at the beginning start. Ptr = temp. Ptr; start. Ptr current. Ptr NULL Node* ? ? ? current. Ptr = start. Ptr; NULL

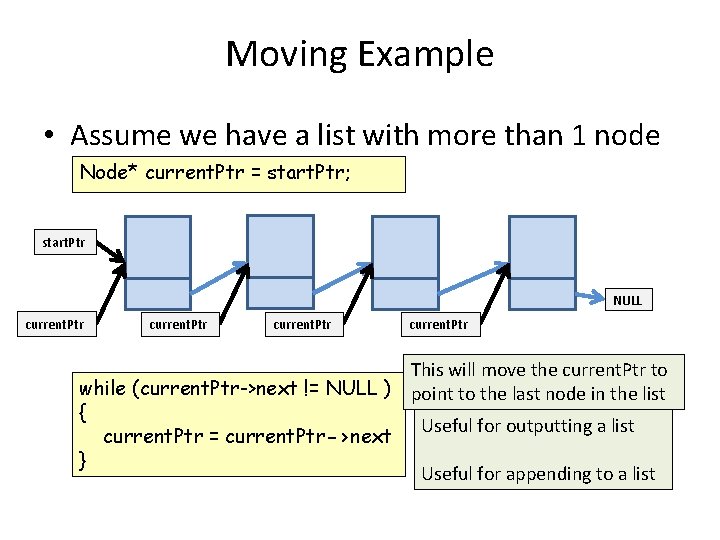
Moving Example • Assume we have a list with more than 1 node Node* current. Ptr = start. Ptr; start. Ptr NULL current. Ptr This will move the current. Ptr to while (current. Ptr->next != NULL ) point to the last node in the list { Useful for outputting a list current. Ptr = current. Ptr->next } Useful for appending to a list

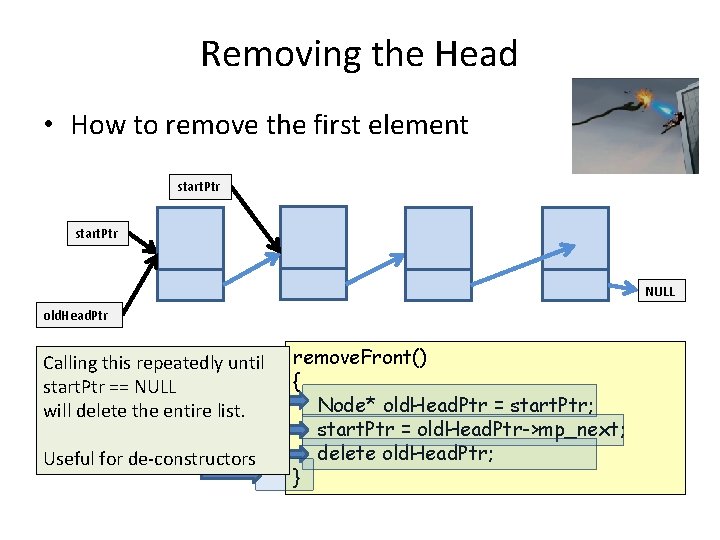
Removing the Head • How to remove the first element start. Ptr NULL old. Head. Ptr Calling this repeatedly until start. Ptr == NULL will delete the entire list. Useful for de-constructors remove. Front() { Node* old. Head. Ptr = start. Ptr; start. Ptr = old. Head. Ptr->mp_next; delete old. Head. Ptr; }

Linked List Class class Node { public: string m_name; int m_age; // age in years Node* mp_next; // pointer to next node }; class My. Linked. List { public: My. Linked. List(); // constructor ~My. Linked. List(); // destructor bool is. Empty() const; // returns true if list is empty Node* find. Node(string find. Name); // returns null or node w/ match void add. Node(const Node& new. Node); // add node to list void remove. Front(); // remove first node of list private: Node* mp_start. Ptr; // pointer to head of list };

Marker Slide • Any Questions on: – Big-Oh • Some Formulas • Examples – Recursion and Iterative Functions – Insertion Sort – Linked Lists • Next up – Free Play

Free Play – Things to Work On • Any not done: Graded In-Class Activities • Homework 6 • Various things to revisit

The End • Or is it?