Big Data Era Bulk Synchronous Parallel Systems Map

“Big Data” Era Bulk Synchronous Parallel Systems: Map. Reduce and Pregel Tuesday, Nov 6 th 2018

Bulk Synchronous Parallel Model of Computation u Computational model underlying many of the systems u E. g: Map. Reduce, Spark, Pregel 2
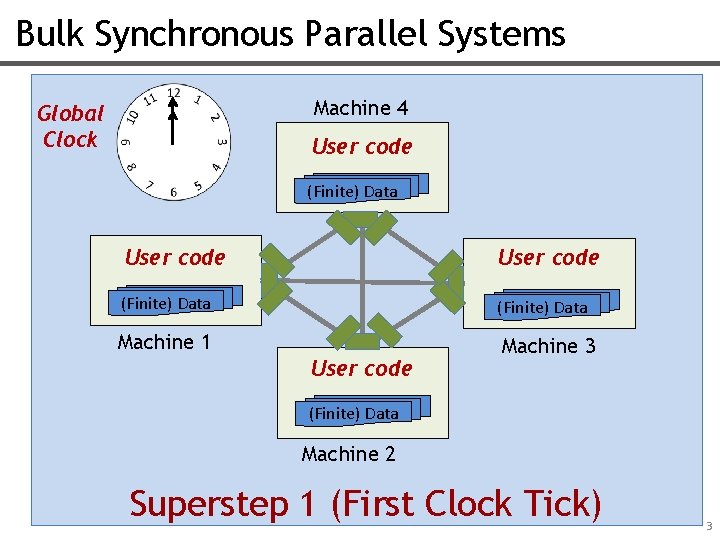
Bulk Synchronous Parallel Systems Machine 4 Global Clock User code (Finite) Data Machine 1 Machine 3 User code (Finite) Data Machine 2 Superstep 1 (First Clock Tick) 3
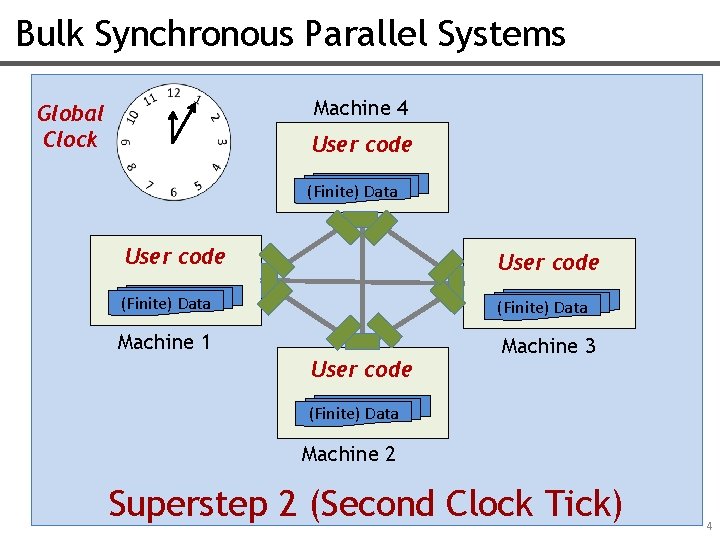
Bulk Synchronous Parallel Systems Machine 4 Global Clock User code (Finite) Data Machine 1 Machine 3 User code (Finite) Data Machine 2 Superstep 2 (Second Clock Tick) 4
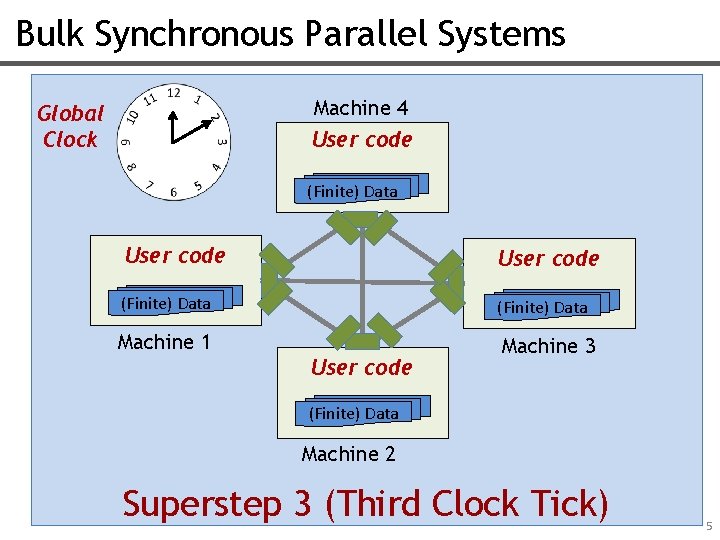
Bulk Synchronous Parallel Systems Machine 4 Global Clock User code (Finite) Data Machine 1 Machine 3 User code (Finite) Data Machine 2 Superstep 3 (Third Clock Tick) 5
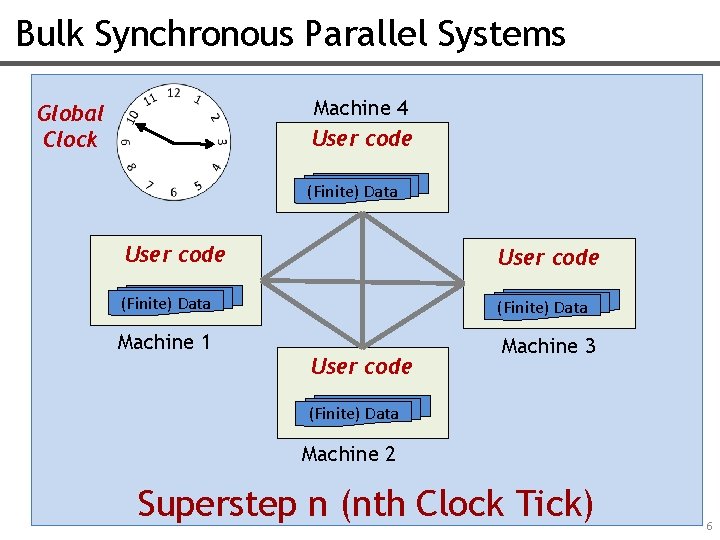
Bulk Synchronous Parallel Systems Machine 4 User code Global Clock (Finite) Data User code (Finite) Data Machine 1 Machine 3 User code (Finite) Data Machine 2 Superstep n (nth Clock Tick) 6

Applications that run on BSP Systems u Many common data processing tasks are 1 -step operations u So BSP is simply very natural for them: § filtering, grouping, joins, projections, sorting, grep u But many other apps as well: § Graph processing § Machine-learning § Linear Algebra, Image Processing, Scientific Simulations § … And many more! 7
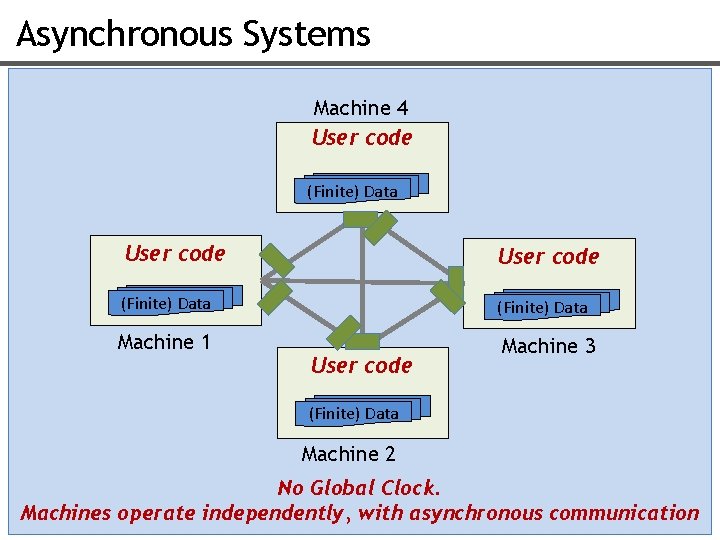
Asynchronous Systems Machine 4 User code (Finite) Data Machine 1 Machine 3 User code (Finite) Data Machine 2 No Global Clock. Machines operate independently, with asynchronous communication 8

Map. Reduce First new era Distributed BSP System 9

“Big Data” Processing Systems in 2006 10
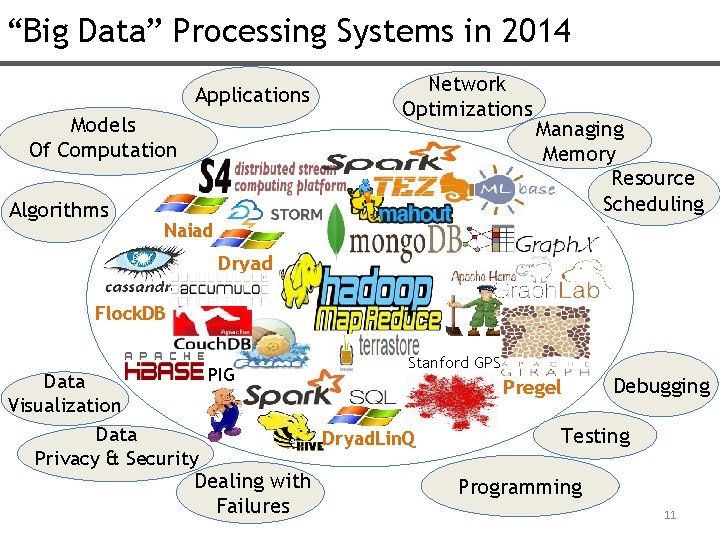
“Big Data” Processing Systems in 2014 Applications Models Of Computation Algorithms Network Optimizations Managing Memory Resource Scheduling Naiad Dryad Flock. DB PIG Data Visualization Data Privacy & Security Dealing with Failures Stanford GPS Pregel Dryad. Lin. Q Debugging Testing Programming 11
Recall: Apps Trigger Research Waves New Set of Applications Database/Data Processing Systems What triggered Map. Reduce? 12
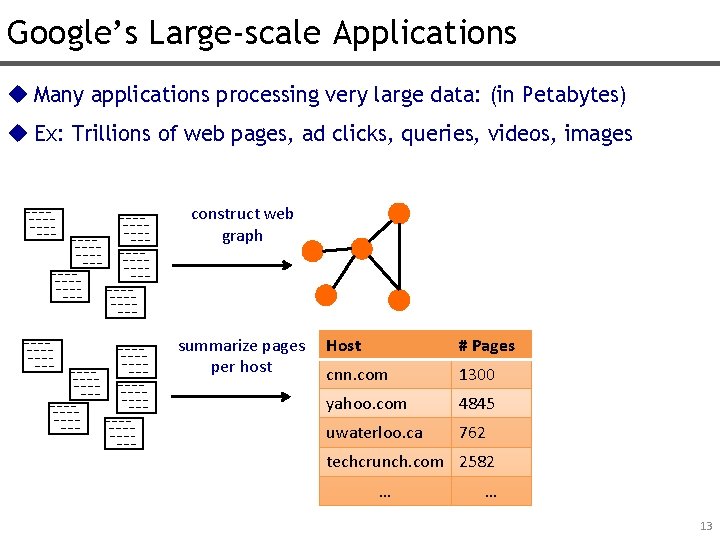
Google’s Large-scale Applications u Many applications processing very large data: (in Petabytes) u Ex: Trillions of web pages, ad clicks, queries, videos, images construct web graph summarize pages per host Host # Pages cnn. com 1300 yahoo. com 4845 uwaterloo. ca 762 techcrunch. com 2582 … … 13

Google’s Large-scale Applications inverted index word Pages trudeau cbc. ca, nytimes. com, wikipedia. org, … apple. com, farming. ca, … computer ibm. com, wikipedia. org, … … user … clicks user 1 cbc. ca user 1 techcrunch. com user 2 wikipedia. com clustering “similar” users (recommendation) user 3 uwaterloo. ca user 3 abc. ca … … u Many others: Ad clicks, videos, images, internal machine logs, etc… 14

Google’s Problem u Need 100 s/1000 s machines to process such large data. Cluster User code Data Machine 1 X User code Data Machine 2 User code … Data M 1 K u But: Writing distributed code is very difficult! Need code for: § Partitioning data. § Communication of machines. § Parallelizing computation. § Dealing with machine failures! § Coordinating the progress. § Others: load-balancing, etc. u All much more complex than the simple application logic! u E. g: Take each web doc. & spit out an edge for each hyperlink 15

“Law of Large-Scale Distributed Systems” u Law of Hardware: Like humans, hardware lives & dies u Consider a super reliable machine: Mean-time-btw-failure: 30 years u At any day prob. failure: ~1/10000 u Consider a distributed system running on 10000 machines Q: Prob a machine will die at any day? A: 64% **Fact of Life: Machines will fail frequently at large-scale. ** 16

Google’s Previous Solution u Special-purpose distributed program for each application. u Problem: Not scalable § Difficult for many engineers to write parallel code § Development speed: Thousands lines for simple applications. § Code repetition for common tasks: § Data Partitioning § Code parallelizing, Fault-tolerance etc. 17

Google’s New Solution: Map. Reduce u Distr. Data Processing System with 3 fundamental properties: 1. Transparent Parallelism § i. e: User-code parallelization & data partitioning automatically done by the system 2. Transparent Fault-tolerance § i. e: Recovery from failures is automatic 3. A Simple Programming API § map() & reduce() These 3 properties also govern any follow-up successful system (e. g. , Spark, Dryad, Pregel, Graph. Lab, etc. ) 18
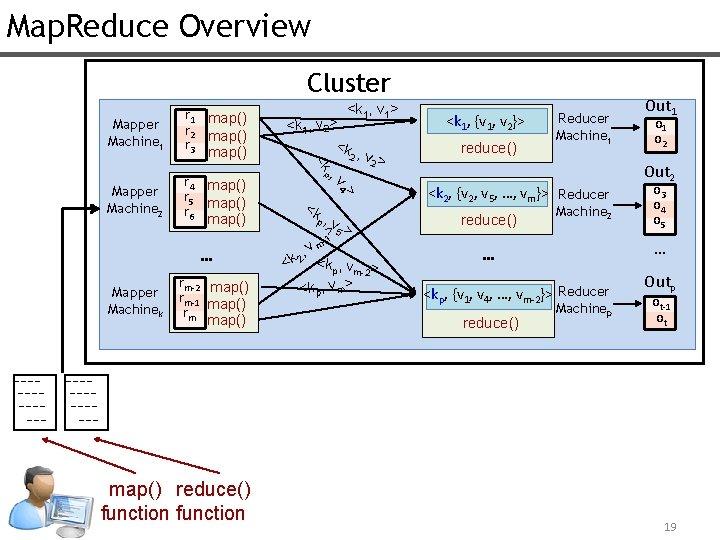
Map. Reduce Overview Cluster map() reduce() function > rm-2 map() rm-1 map() rm map() 4 Mapper Machinek , v … <k 1, v 2> <k , 2 v > 2 <k 1, {v 1, v 2}> reduce() Reducer Machine 1 p Mapper Machine 2 r 4 map() r 5 map() r 6 map() <k 1, v 1> <k Mapper Machine 1 r 1 map() r 2 map() r 3 map() <k p, - v 5 > > 1 , vm 2 <k <kp, vm-2> <kp, vm> <k 2, {v 2, v 5, …, vm}> Reducer reduce() Machine 2 o 1 o 2 Out 2 o 3 o 4 o 5 … … <kp, {v 1, v 4, …, vm-2}> Reducer reduce() Out 1 Machinep Outp ot-1 ot 19
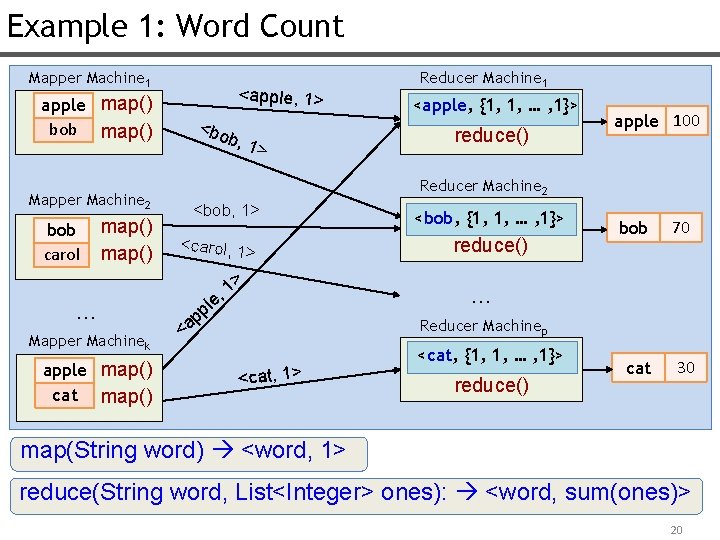
Example 1: Word Count Mapper Machine 1 apple map() bob map() Mapper Machine 2 bob carol map() … Mapper Machinek apple map() cat map() <apple, 1> <bo b, 1 > Reducer Machine 1 <apple, {1, 1, … , 1}> reduce() apple 100 Reducer Machine 2 <bob, 1> <carol, 1> > 1 , e pl p a < <bob, {1, 1, … , 1}> reduce() bob 70 cat 30 … Reducer Machinep <cat, 1> <cat, {1, 1, … , 1}> reduce() map(String word) <word, 1> reduce(String word, List<Integer> ones): <word, sum(ones)> 20
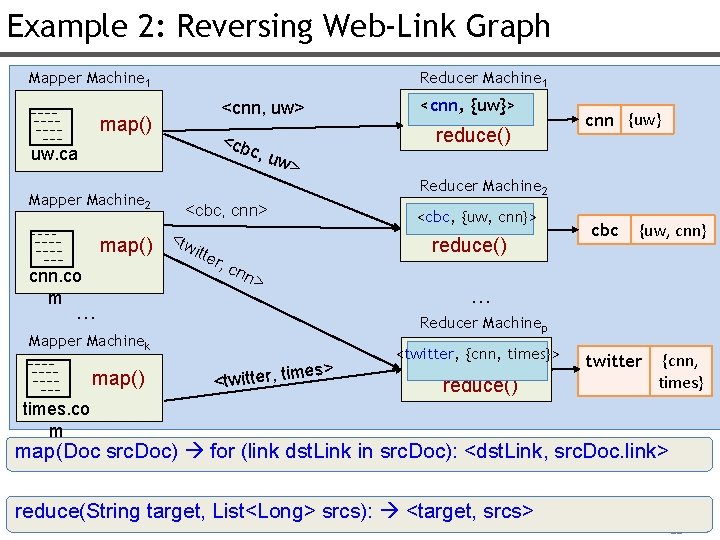
Example 2: Reversing Web-Link Graph Mapper Machine 1 Reducer Machine 1 map() uw. ca Mapper Machine 2 map() cnn. co m <cnn, uw> <cnn, {uw}> <cb c, u w> reduce() Reducer Machine 2 <cbc, cnn> <tw itte <cbc, {uw, cnn}> reduce() r, c cbc {uw, cnn} nn > … … Reducer Machinep Mapper Machinek map() cnn {uw} es> <twitter, tim <twitter, {cnn, times}> reduce() twitter {cnn, times} times. co m map(Doc src. Doc) for (link dst. Link in src. Doc): <dst. Link, src. Doc. link> reduce(String target, List<Long> srcs): <target, srcs> 21
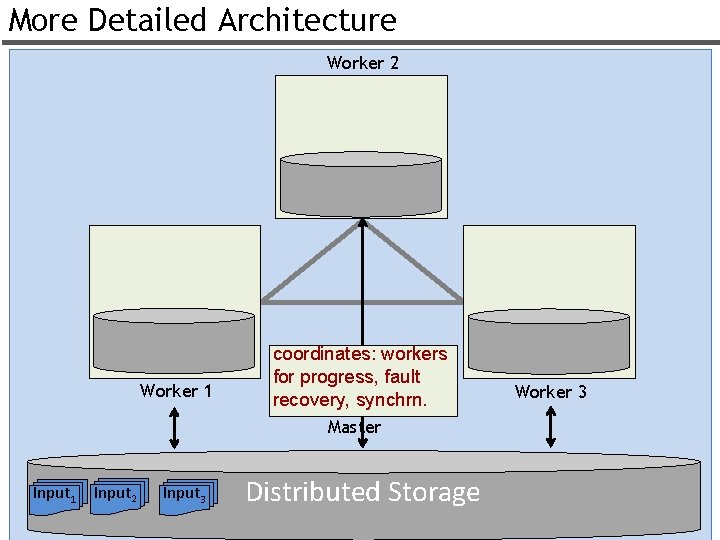
More Detailed Architecture Worker 2 Worker 1 coordinates: workers for progress, fault recovery, synchrn. Worker 3 Master Input 1 Input 2 Input 3 Distributed Storage 22
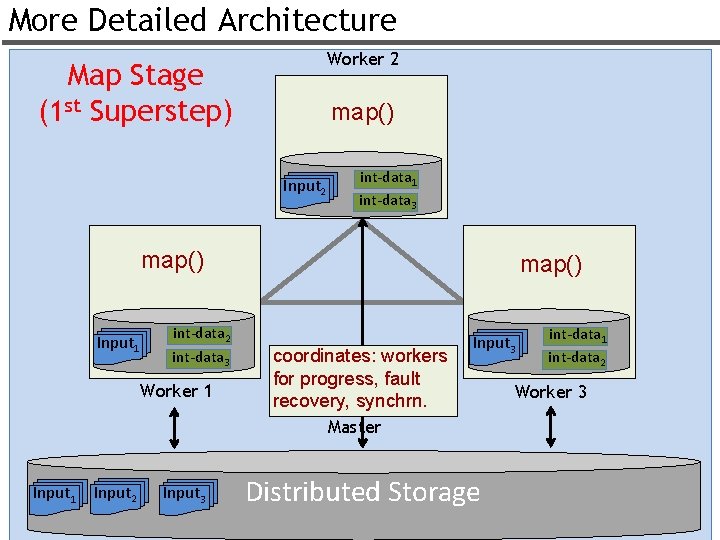
More Detailed Architecture Worker 2 Map Stage (1 st Superstep) map() Input 2 int-data 1 int-data 3 map() Input 1 int-data 2 int-data 3 Worker 1 map() coordinates: workers for progress, fault recovery, synchrn. Input 3 int-data 1 int-data 2 Worker 3 Master Input 1 Input 2 Input 3 Distributed Storage 23
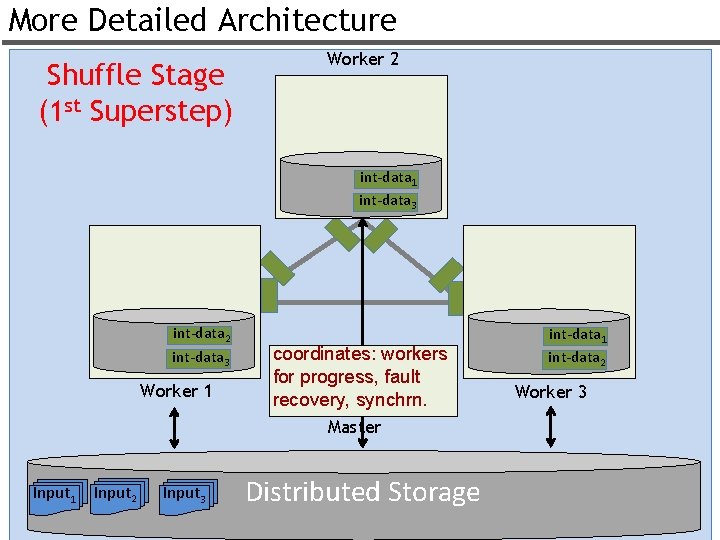
More Detailed Architecture Shuffle Stage (1 st Superstep) Worker 2 int-data 1 int-data 3 int-data 2 int-data 3 Worker 1 coordinates: workers for progress, fault recovery, synchrn. int-data 1 int-data 2 Worker 3 Master Input 1 Input 2 Input 3 Distributed Storage 24
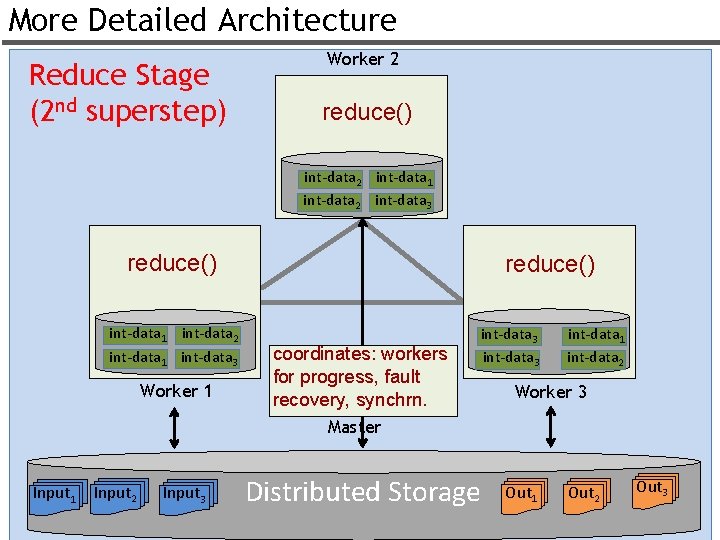
More Detailed Architecture Reduce Stage (2 nd superstep) Worker 2 reduce() int-data 2 int-data 1 int-data 2 int-data 3 reduce() int-data 1 int-data 2 int-data 1 int-data 3 Worker 1 reduce() coordinates: workers for progress, fault recovery, synchrn. int-data 3 int-data 1 int-data 2 Worker 3 Master Input 1 Input 2 Input 3 Distributed Storage Out 1 Out 2 Out 3 25
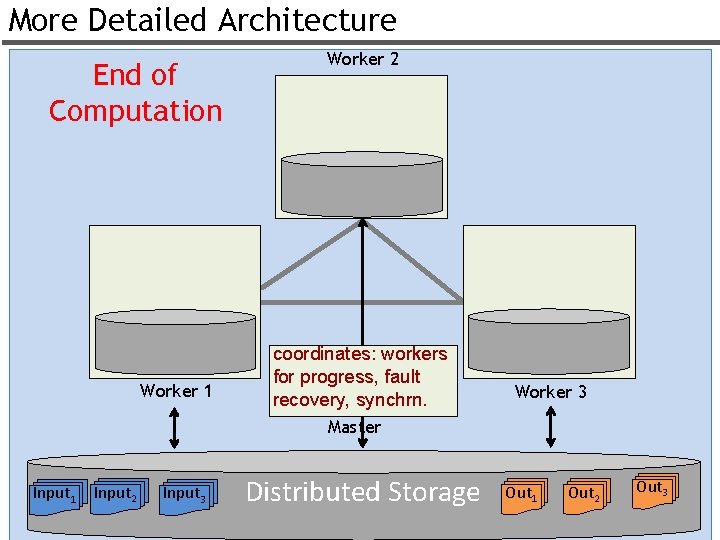
More Detailed Architecture End of Computation Worker 1 Worker 2 coordinates: workers for progress, fault recovery, synchrn. Worker 3 Master Input 1 Input 2 Input 3 Distributed Storage Out 1 Out 2 Out 3 26

Fault Tolerance u 3 Failure Scenarios 1. Master Failure: Nothing is done. Computation Fails. 2. Mapper Failure (next slide) 3. Reducer Failure (next slide) 27
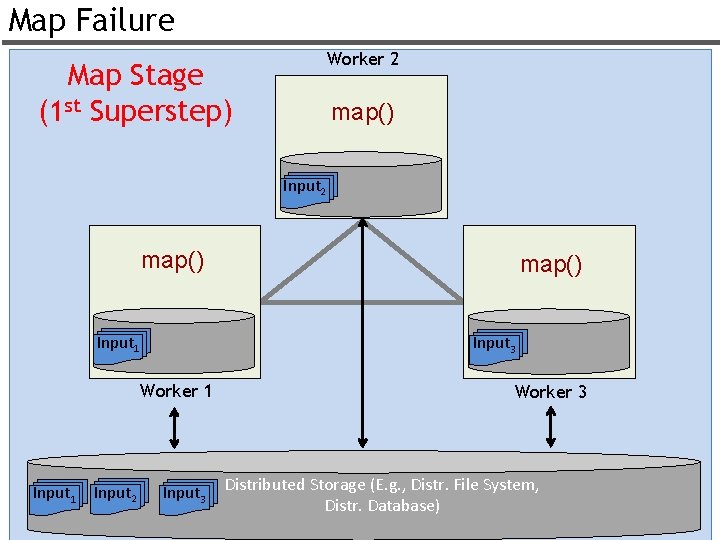
Map Failure Worker 2 Map Stage (1 st Superstep) map() Input 2 map() Input 1 Input 3 Worker 1 Input 2 map() Input 3 Worker 3 Distributed Storage (E. g. , Distr. File System, Distr. Database) 28

Map Failure Worker 2 Map Stage (1 st Superstep) map() Input 2 X int-data 1 int-data 3 map() Input 1 Worker 1 Input 2 Input 3 map() Input 3 int-data 1 int-data 2 Worker 3 Distributed Storage (E. g. , Distr. File System, Distr. Database) 29
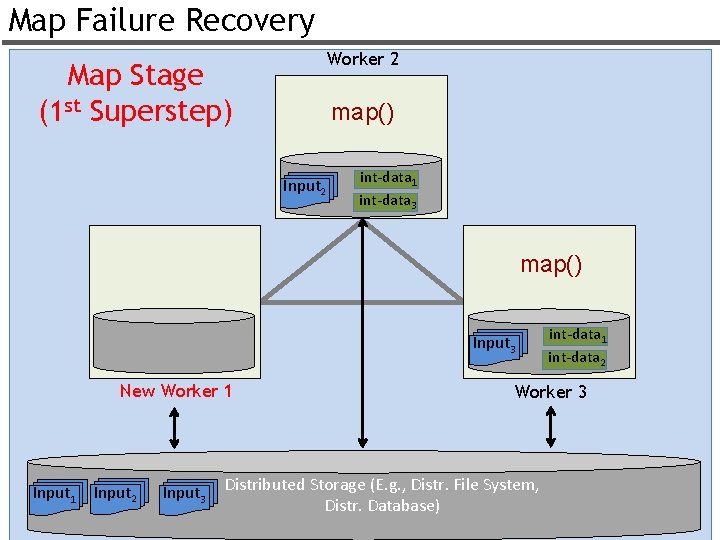
Map Failure Recovery Worker 2 Map Stage (1 st Superstep) map() Input 2 int-data 1 int-data 3 map() Input 3 New Worker 1 Input 2 Input 3 int-data 1 int-data 2 Worker 3 Distributed Storage (E. g. , Distr. File System, Distr. Database) 30
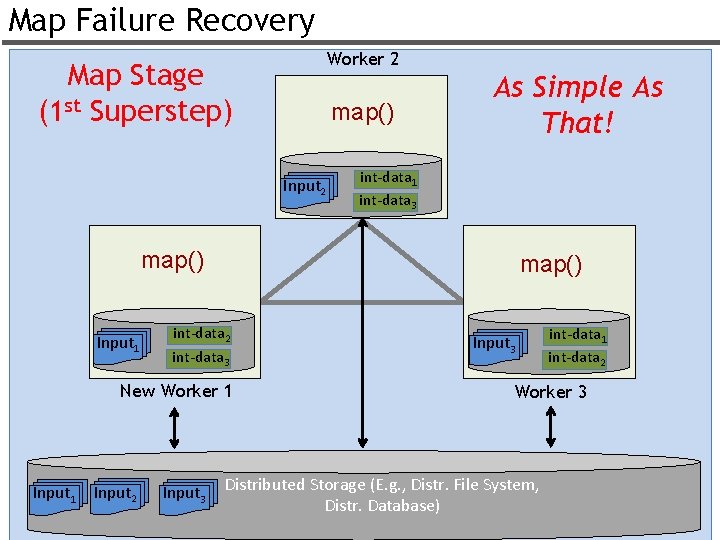
Map Failure Recovery Worker 2 Map Stage (1 st Superstep) map() Input 2 As Simple As That! int-data 1 int-data 3 map() Input 1 map() int-data 2 int-data 3 New Worker 1 Input 2 Input 3 int-data 1 int-data 2 Worker 3 Distributed Storage (E. g. , Distr. File System, Distr. Database) 31
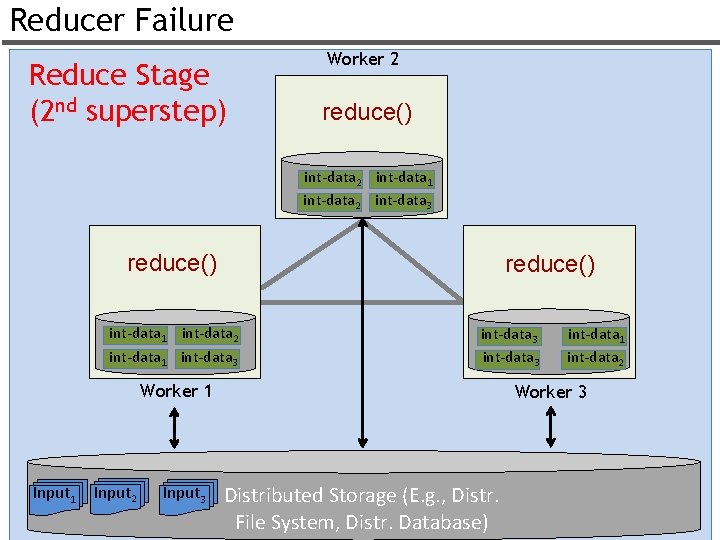
Reducer Failure Reduce Stage (2 nd superstep) Worker 2 reduce() int-data 2 int-data 1 int-data 2 int-data 3 reduce() int-data 1 int-data 2 int-data 1 int-data 3 Worker 1 Input 2 Input 3 int-data 1 int-data 2 Worker 3 Distributed Storage (E. g. , Distr. File System, Distr. Database) 32
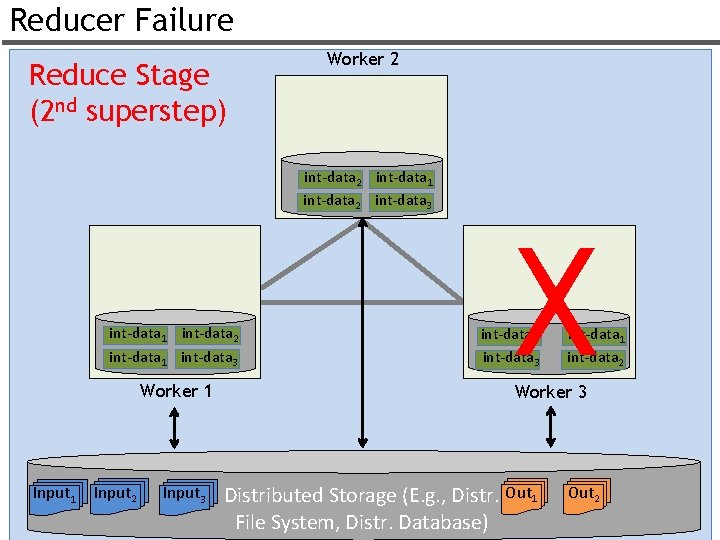
Reducer Failure Reduce Stage (2 nd superstep) Worker 2 int-data 1 int-data 2 int-data 3 int-data 1 int-data 2 int-data 1 int-data 3 Worker 1 Input 2 Input 3 X int-data 3 int-data 1 int-data 2 Worker 3 Distributed Storage (E. g. , Distr. Out 1 File System, Distr. Database) Out 2 33
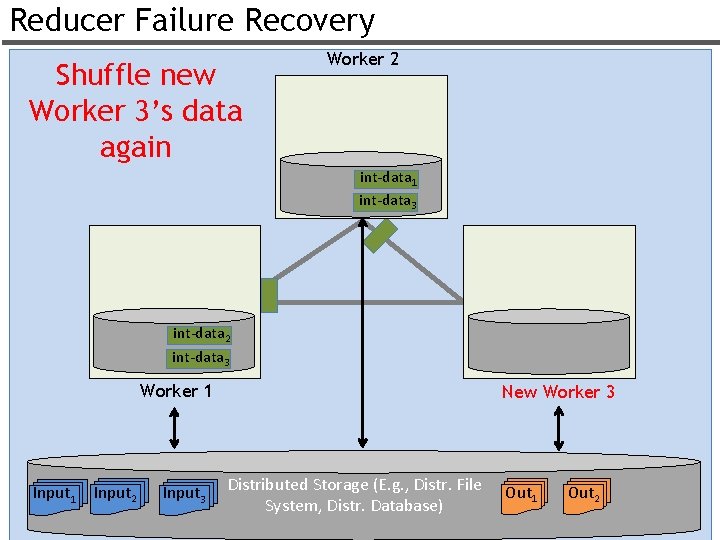
Reducer Failure Recovery Shuffle new Worker 3’s data again Worker 2 int-data 1 int-data 3 int-data 2 int-data 3 Worker 1 Input 2 Input 3 New Worker 3 Distributed Storage (E. g. , Distr. File System, Distr. Database) Out 1 Out 2 34
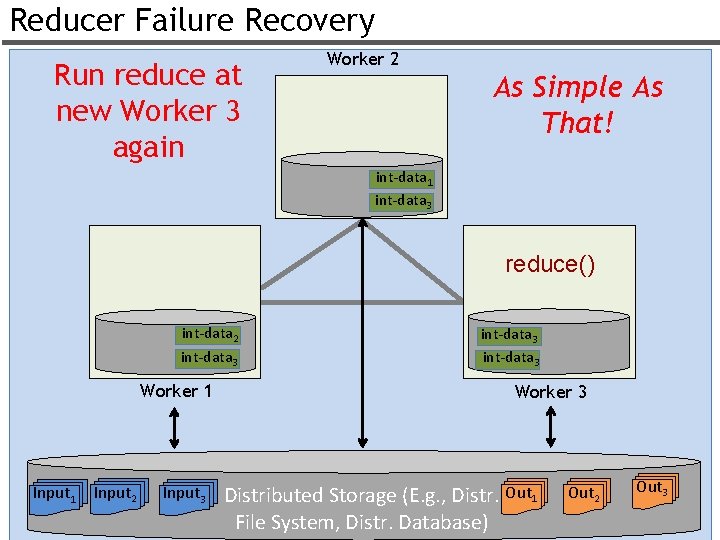
Reducer Failure Recovery Run reduce at new Worker 3 again Worker 2 As Simple As That! int-data 1 int-data 3 reduce() int-data 2 int-data 3 Worker 1 Input 2 Input 3 int-data 3 Worker 3 Distributed Storage (E. g. , Distr. Out 1 File System, Distr. Database) Out 2 Out 3 35
Importance of Map. Reduce u Role model for existing distributed data processing systems: 1. Transparent Parallelism 2. Transparent Fault-Tolerance 3. Programming API: Focus only on Application Logic u Examples: u Spark u Pregel, Graph. Lab: Graph/ML Processing Systems u Mill. Wheel: Streaming u Many others 36

Shortcomings of MR for Graph Algorithms u Most batch graph algorithms are iterative: u Page. Rank takes 100 s of iterations to converge. u Bellman-Ford can take 1000 s of iterations to converge. u many more… MR: inefficient b/c input and msgs hit disk in each iteration. 37
![Example: Page. Rank(G(V, E)): prev. PRs = new double[|V|] next. PRs = new double[|V|] Example: Page. Rank(G(V, E)): prev. PRs = new double[|V|] next. PRs = new double[|V|]](http://slidetodoc.com/presentation_image_h2/a9855e55faa443d5ebcf2ee4083135d8/image-38.jpg)
Example: Page. Rank(G(V, E)): prev. PRs = new double[|V|] next. PRs = new double[|V|] for (iter 1. . 50): for (v ∈ V): next. PRs[v] = sum(prev. PRs[w]|(w, v)∈E)*0. 8 + 0. 1 prev. PRs ↔� next. PRs 38
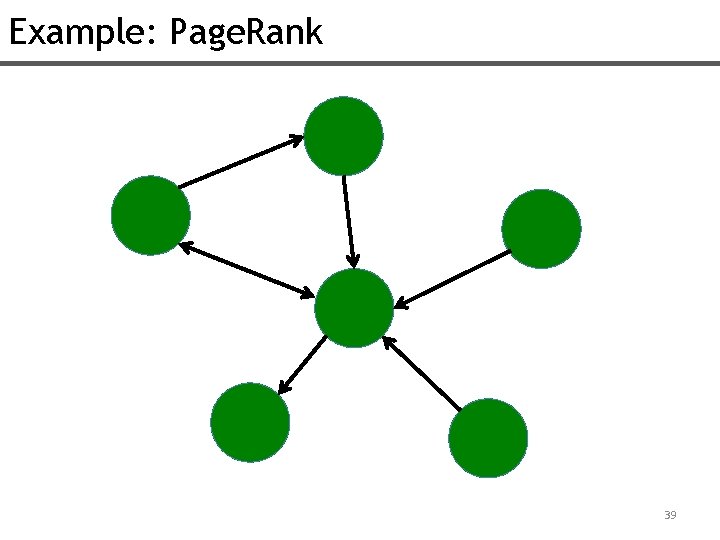
Example: Page. Rank 39
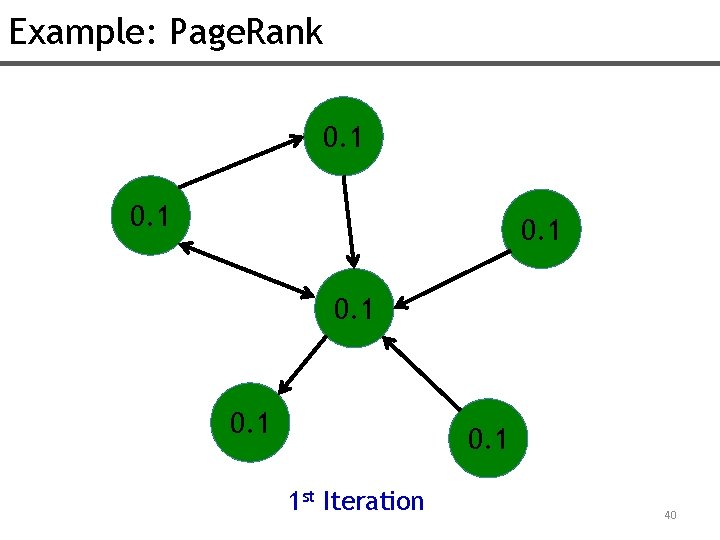
Example: Page. Rank 0. 1 0. 1 1 st Iteration 40
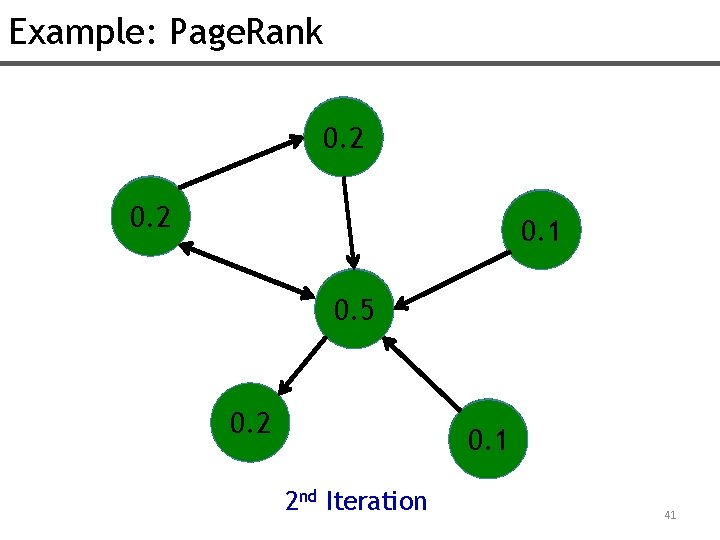
Example: Page. Rank 0. 1 0. 2 0. 1 0. 5 0. 1 0. 2 0. 1 2 nd Iteration 41
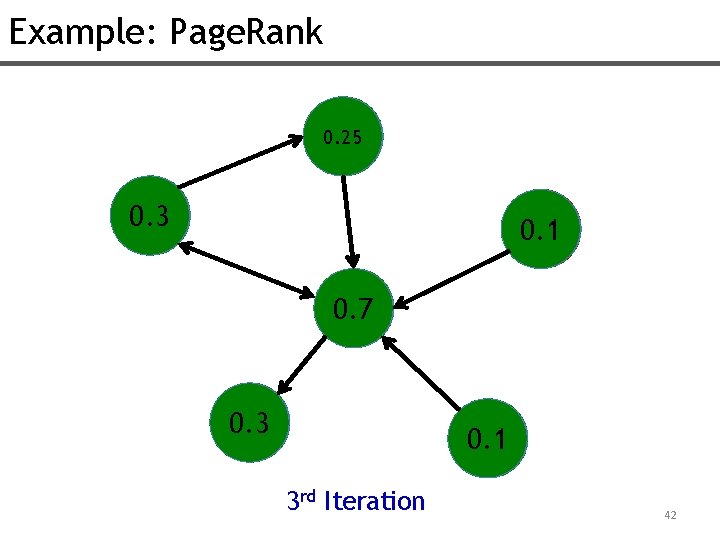
Example: Page. Rank 0. 25 0. 2 0. 3 0. 2 0. 1 0. 7 0. 5 0. 3 0. 2 0. 1 3 rd Iteration 42
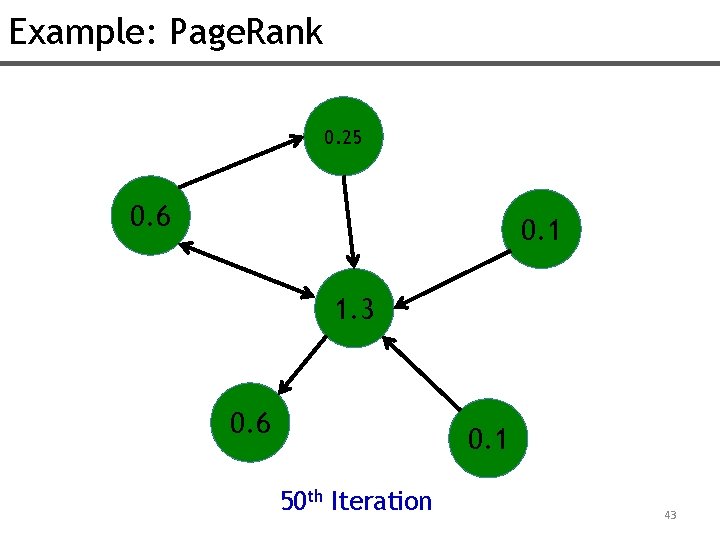
Example: Page. Rank 0. 25 0. 6 0. 1 1. 3 0. 6 0. 1 50 th Iteration 43
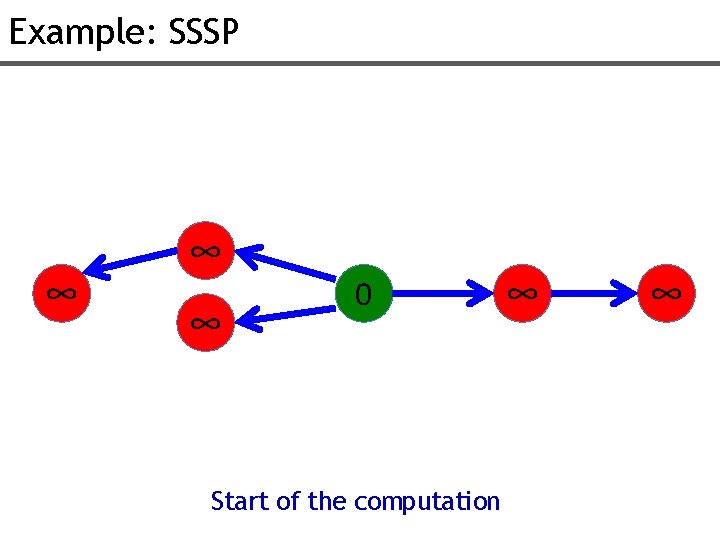
Example: SSSP ∞ ∞ ∞ 0 Start of the computation ∞ ∞
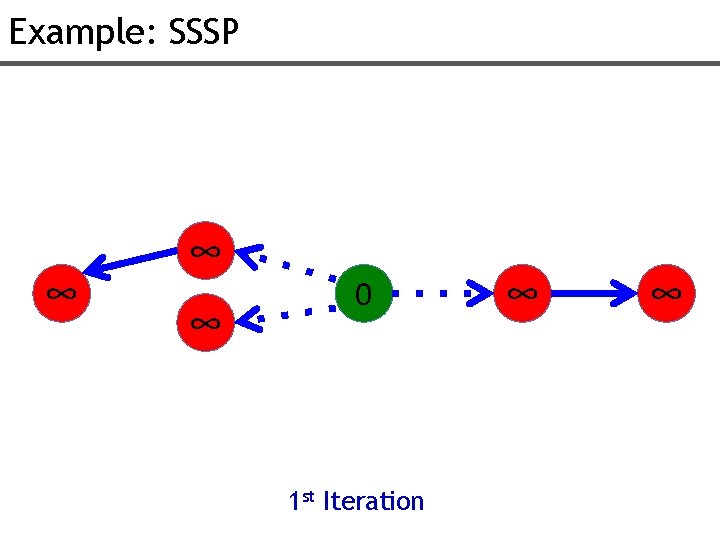
Example: SSSP ∞ ∞ ∞ 0 1 st Iteration ∞ ∞
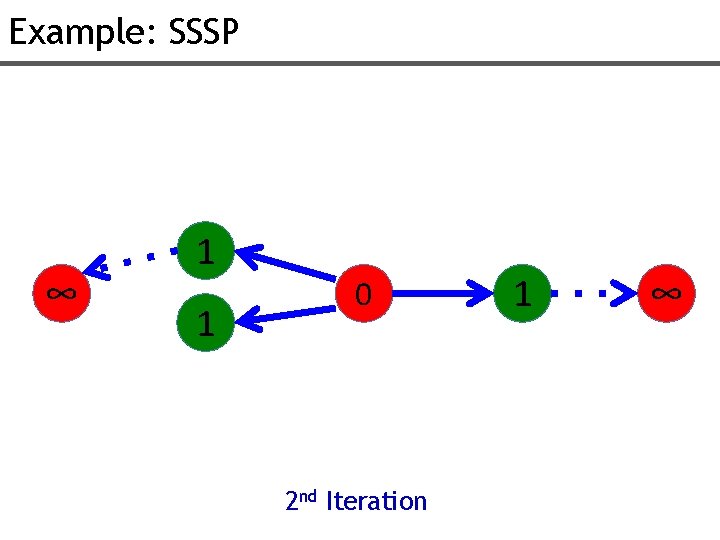
Example: SSSP ∞ 1 1 0 2 nd Iteration 1 ∞
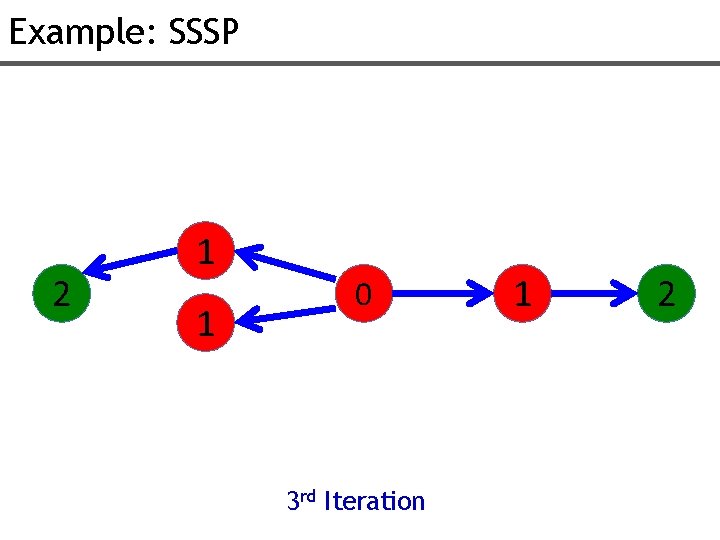
Example: SSSP 2 1 1 0 3 rd Iteration 1 2
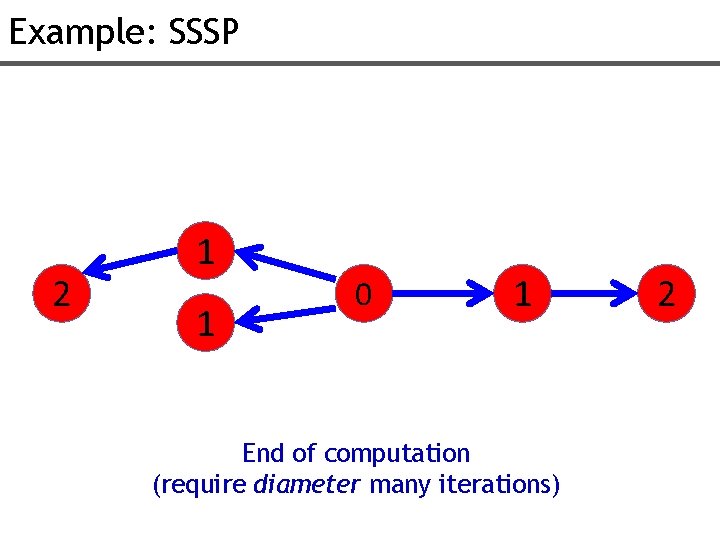
Example: SSSP 2 1 1 0 1 End of computation (require diameter many iterations) 2
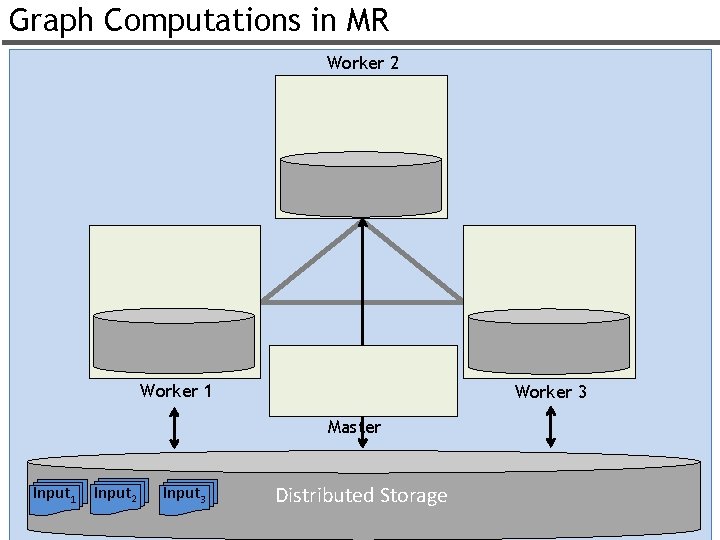
Graph Computations in MR Worker 2 Worker 1 Worker 3 Master Input 1 Input 2 Input 3 Distributed Storage 49
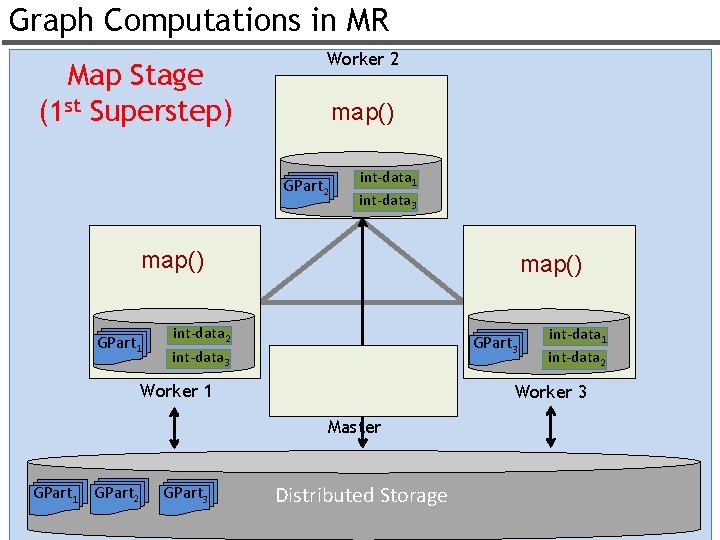
Graph Computations in MR Map Stage (1 st Superstep) Worker 2 map() GPart 2 int-data 1 int-data 3 map() GPart 1 map() int-data 2 int-data 3 GPart 3 Worker 1 int-data 2 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage 50
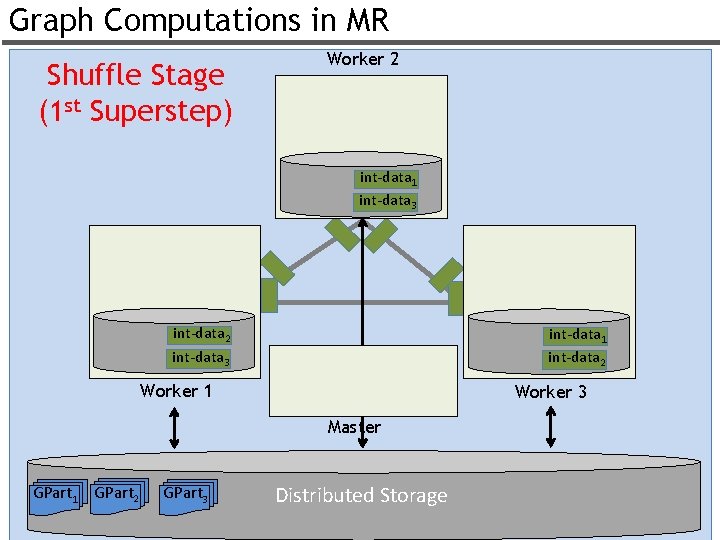
Graph Computations in MR Shuffle Stage (1 st Superstep) Worker 2 int-data 1 int-data 3 int-data 2 int-data 3 int-data 1 int-data 2 Worker 1 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage 51
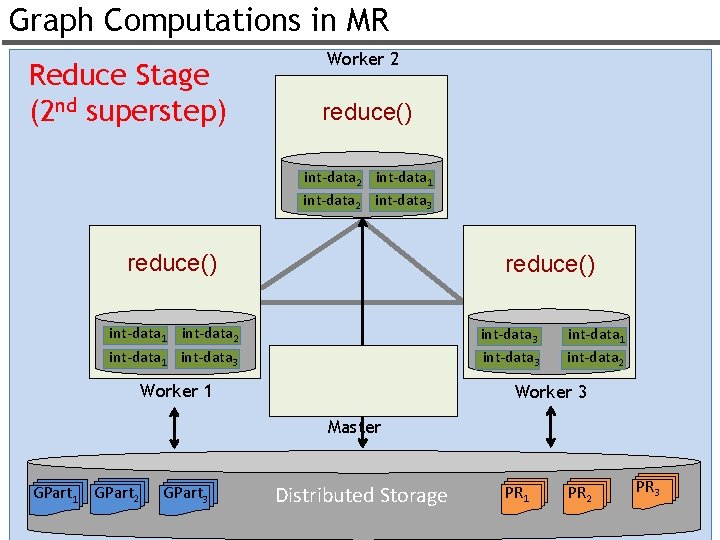
Graph Computations in MR Reduce Stage (2 nd superstep) Worker 2 reduce() int-data 2 int-data 1 int-data 2 int-data 3 reduce() int-data 1 int-data 2 int-data 1 int-data 3 Worker 1 int-data 2 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage PR 1 PR 2 PR 3 52
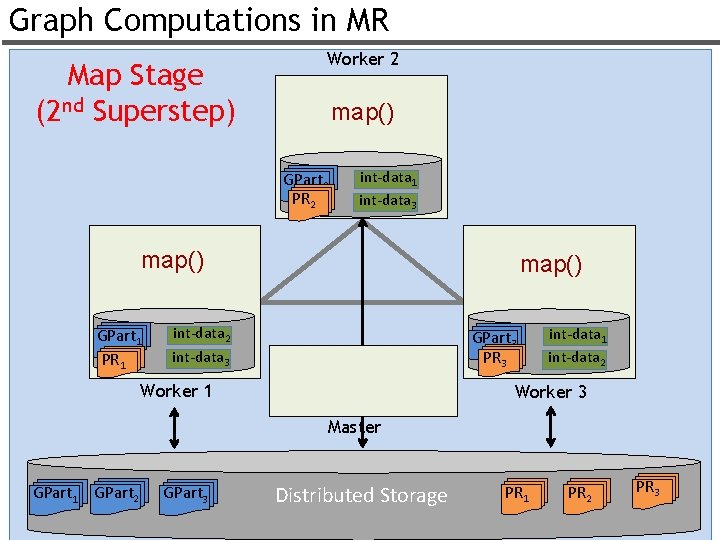
Graph Computations in MR Map Stage (2 nd Superstep) Worker 2 map() GPart 2 PR 2 int-data 1 int-data 3 map() GPart 1 PR 1 map() int-data 2 int-data 3 GPart 3 PR 3 Worker 1 int-data 2 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage PR 1 PR 2 PR 3 53
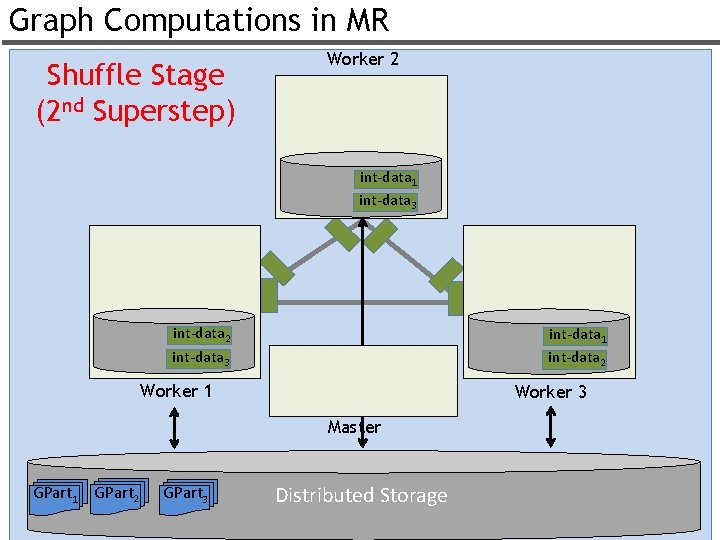
Graph Computations in MR Shuffle Stage (2 nd Superstep) Worker 2 int-data 1 int-data 3 int-data 2 int-data 3 int-data 1 int-data 2 Worker 1 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage 54
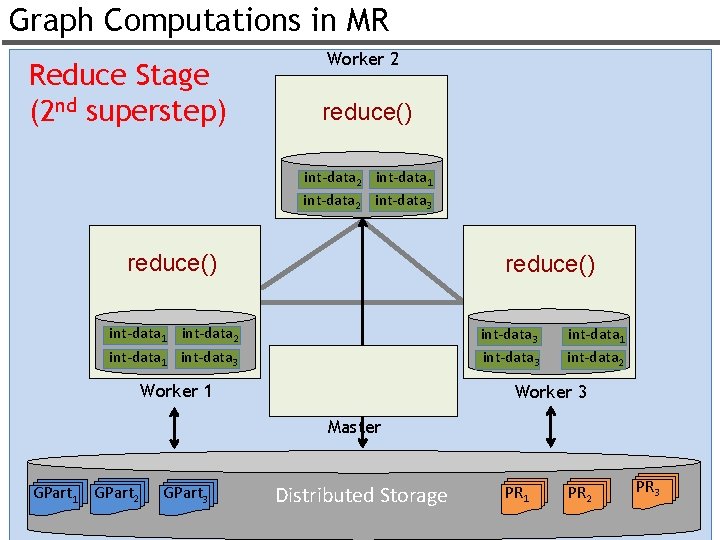
Graph Computations in MR Reduce Stage (2 nd superstep) Worker 2 reduce() int-data 2 int-data 1 int-data 2 int-data 3 reduce() int-data 1 int-data 2 int-data 1 int-data 3 Worker 1 int-data 2 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage PR 1 PR 2 PR 3 55
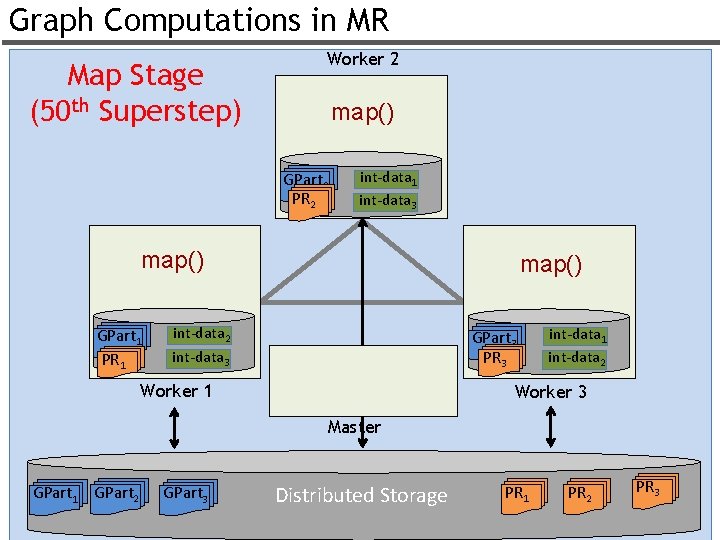
Graph Computations in MR Map Stage (50 th Superstep) Worker 2 map() GPart 2 PR 2 int-data 1 int-data 3 map() GPart 1 PR 1 map() int-data 2 int-data 3 GPart 3 PR 3 Worker 1 int-data 2 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage PR 1 PR 2 PR 3 56
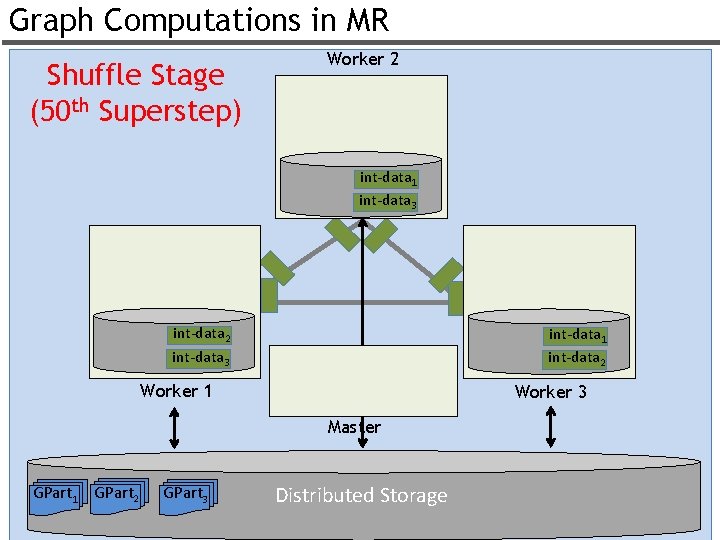
Graph Computations in MR Shuffle Stage (50 th Superstep) Worker 2 int-data 1 int-data 3 int-data 2 int-data 3 int-data 1 int-data 2 Worker 1 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage 57
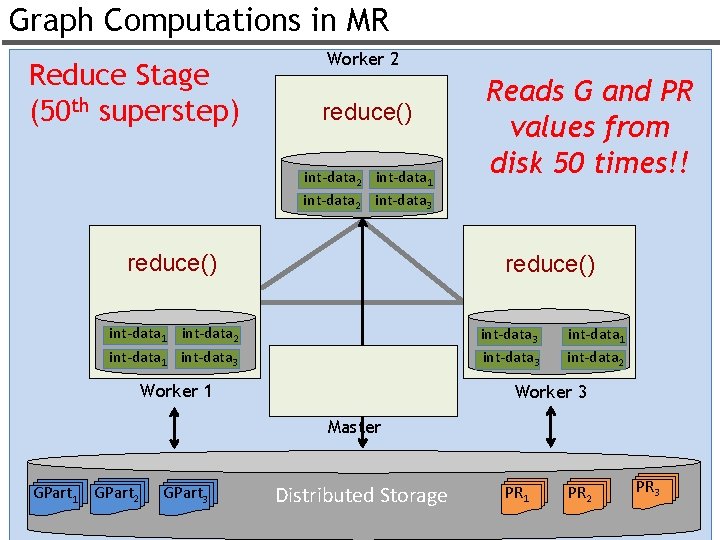
Graph Computations in MR Reduce Stage (50 th superstep) Worker 2 reduce() int-data 2 int-data 1 int-data 2 int-data 3 reduce() Reads G and PR values from disk 50 times!! reduce() int-data 1 int-data 2 int-data 1 int-data 3 Worker 1 int-data 2 Worker 3 Master GPart 1 GPart 2 GPart 3 Distributed Storage PR 1 PR 2 PR 3 58
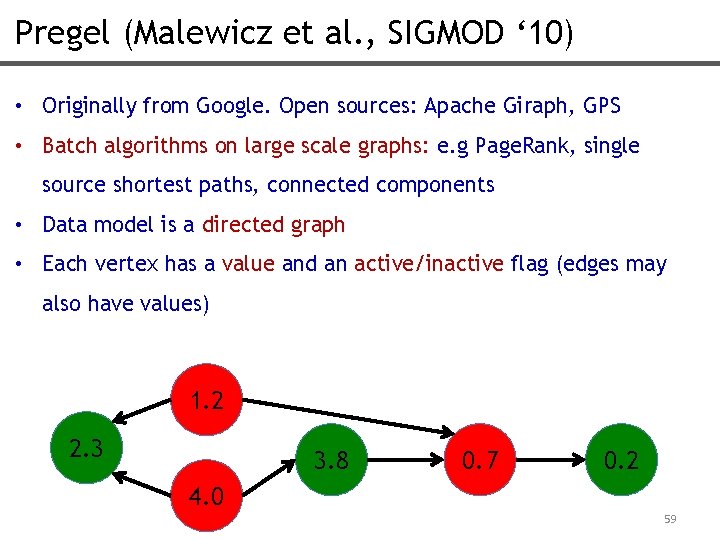
Pregel (Malewicz et al. , SIGMOD ‘ 10) • Originally from Google. Open sources: Apache Giraph, GPS • Batch algorithms on large scale graphs: e. g Page. Rank, single source shortest paths, connected components • Data model is a directed graph • Each vertex has a value and an active/inactive flag (edges may also have values) 1. 2 2. 3 3. 8 0. 7 0. 2 4. 0 59
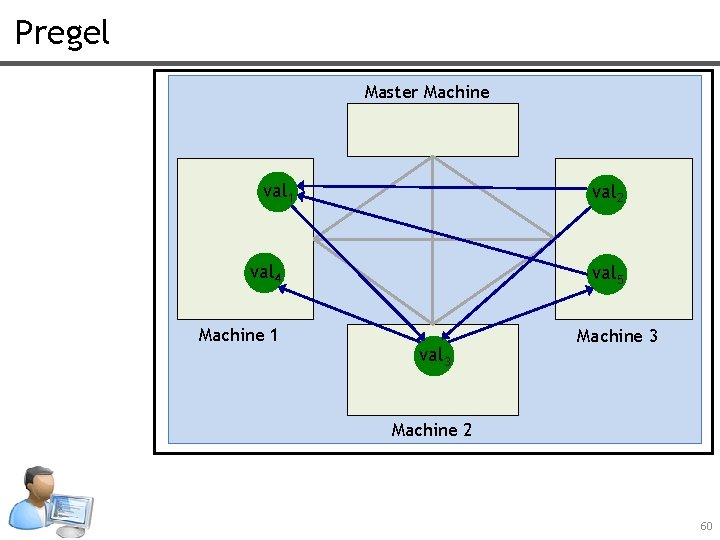
Pregel Master Machine val 1 val 2 val 4 Machine 1 val 5 val 3 Machine 2 60
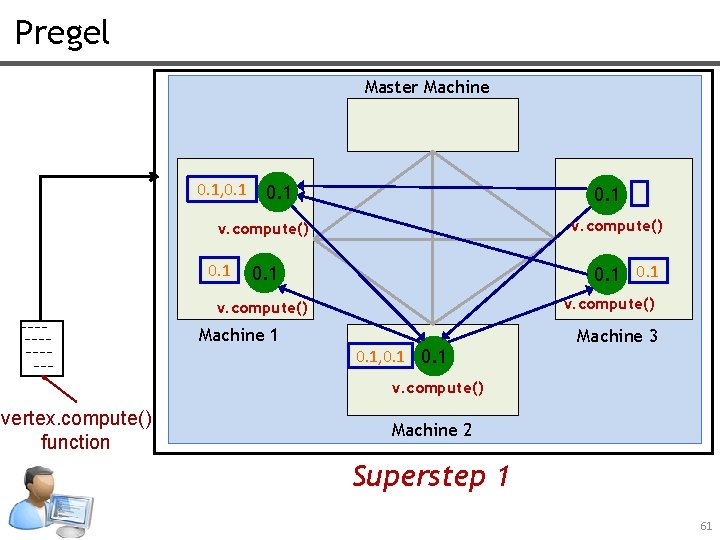
Pregel Master Machine 0. 1, 0. 1 0. 1 v. compute() Machine 1 0. 1, 0. 1 Machine 3 v. compute() vertex. compute() function Machine 2 Superstep 1 61
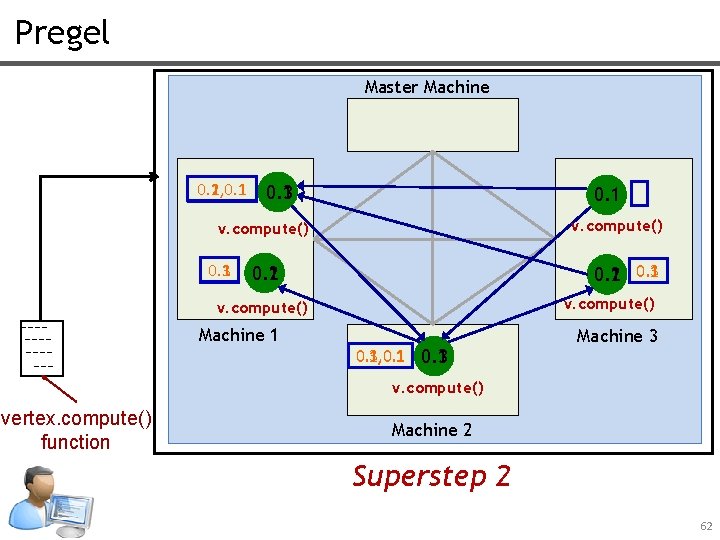
Pregel Master Machine 0. 2, 0. 1 0. 3 0. 1 v. compute() 0. 3 0. 1 0. 2 0. 3 0. 1 0. 2 v. compute() Machine 1 0. 3, 0. 1, 0. 1 0. 3 0. 1 Machine 3 v. compute() vertex. compute() function Machine 2 Superstep 2 62
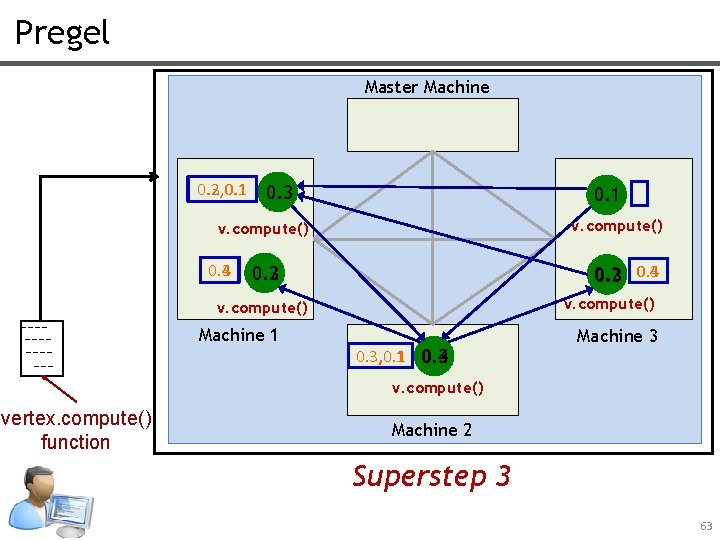
Pregel Master Machine 0. 3, 0. 1 0. 2, 0. 1 0. 3 0. 1 v. compute() 0. 4 0. 3 0. 4 0. 2 0. 3 v. compute() Machine 1 0. 3, 0. 1 0. 3 0. 4 Machine 3 v. compute() vertex. compute() function Machine 2 Superstep 3 63
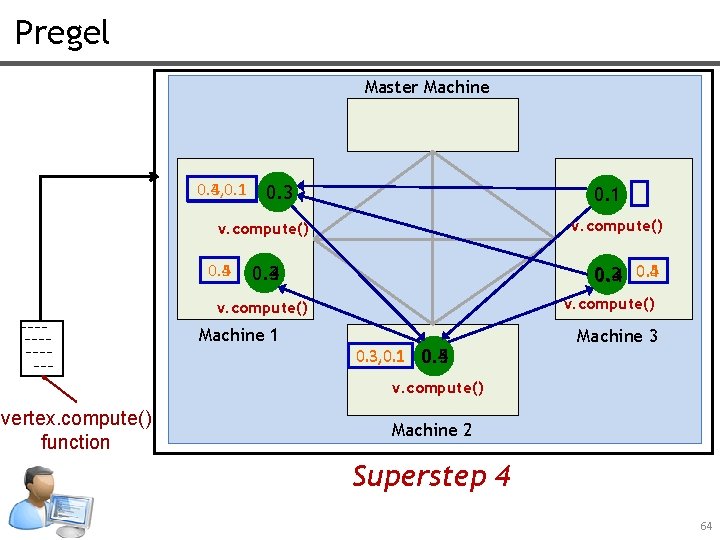
Pregel Master Machine 0. 4, 0. 1 0. 3 0. 1 v. compute() 0. 5 0. 4 0. 3 0. 4 0. 5 0. 3 0. 4 v. compute() Machine 1 0. 3, 0. 1 0. 4 0. 5 Machine 3 v. compute() vertex. compute() function Machine 2 Superstep 4 64
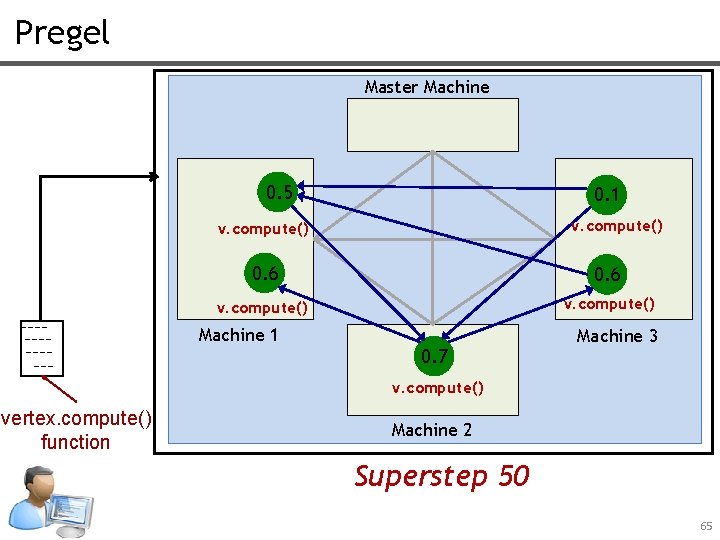
Pregel Master Machine 0. 5 0. 1 v. compute() 0. 6 v. compute() Machine 1 0. 7 Machine 3 v. compute() vertex. compute() function Machine 2 Superstep 50 65

Programming API: Vertex. compute() public void compute(Iterable<Msg> msgs) { if (get. Iteration. No() == 1) { update. Value(0. 1); } else { double sum = sum. Msgs(msgs) double new. Value = sum*0. 85 + 0. 15; update. Value(new. Value); send. Msg. To. All. Nbrs(new. Value); } … } 66
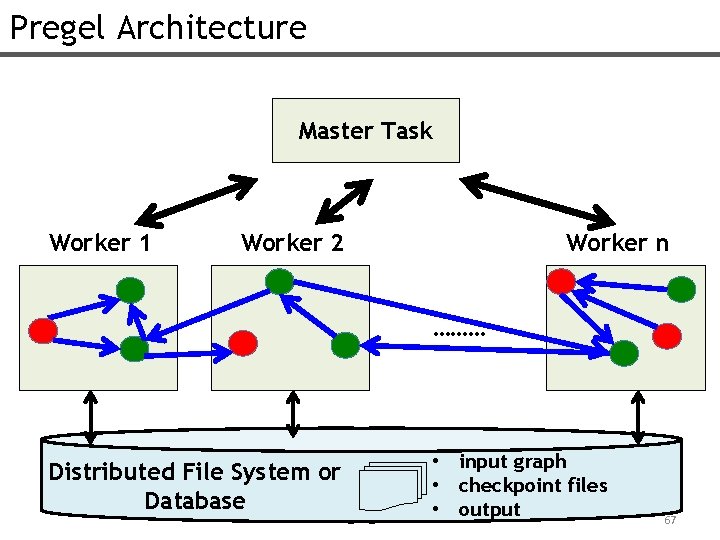
Pregel Architecture Master Task Worker 1 Worker 2 Worker n ……… Distributed File System or Database • input graph • checkpoint files • output 67

Pregel Architecture • Bulk Synchronous message-passing computation • Inherently iterative • Graph data and vertex values always remain in RAM • Fault-tolerant by simple checkpointing between iterations • Several Other Optimizations/Extensions: • Combiners • Master. compute() (currently in Giraph) 68
- Slides: 68