Biegung Prof Dr Remo Ianniello Inhalt In diesem

Biegung © Prof. Dr. Remo Ianniello

Inhalt In diesem Foliensatz geht es um: Biegespannung FTM Flächenträgheitsmoment Satz von Steiner Durchbiegung © Copyright: Der Inhalt dieser Folien darf - mit Quellenangabe - kopiert und weiter gegeben werden. Biegung © Prof. Dr. Remo Ianniello Folie 2

Biegespannun g Biegung © Prof. Dr. Remo Ianniello Folie 3

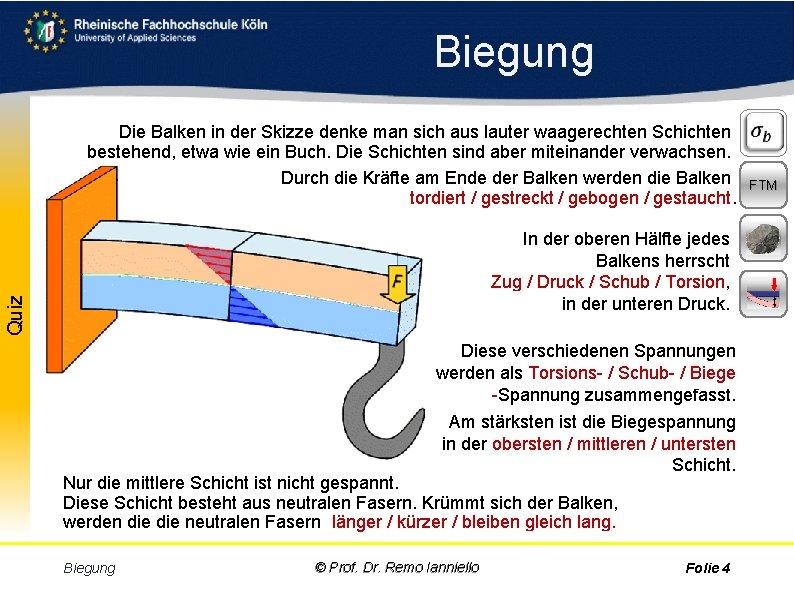
Biegung Die Balken in der Skizze denke man sich aus lauter waagerechten Schichten bestehend, etwa wie ein Buch. Die Schichten sind aber miteinander verwachsen. Durch die Kräfte am Ende der Balken werden die Balken FTM tordiert / gestreckt / gebogen / gestaucht. Aufgabe Quiz In der oberen Hälfte jedes Balkens herrscht Zug / Druck / Schub / Torsion, in der unteren Druck. Diese verschiedenen Spannungen werden als Torsions / Schub / Biege Spannung zusammengefasst. Am stärksten ist die Biegespannung in der obersten / mittleren / untersten Schicht. Nur die mittlere Schicht ist nicht gespannt. Diese Schicht besteht aus neutralen Fasern. Krümmt sich der Balken, werden die neutralen Fasern länger / kürzer / bleiben gleich lang. Biegung © Prof. Dr. Remo Ianniello Folie 4

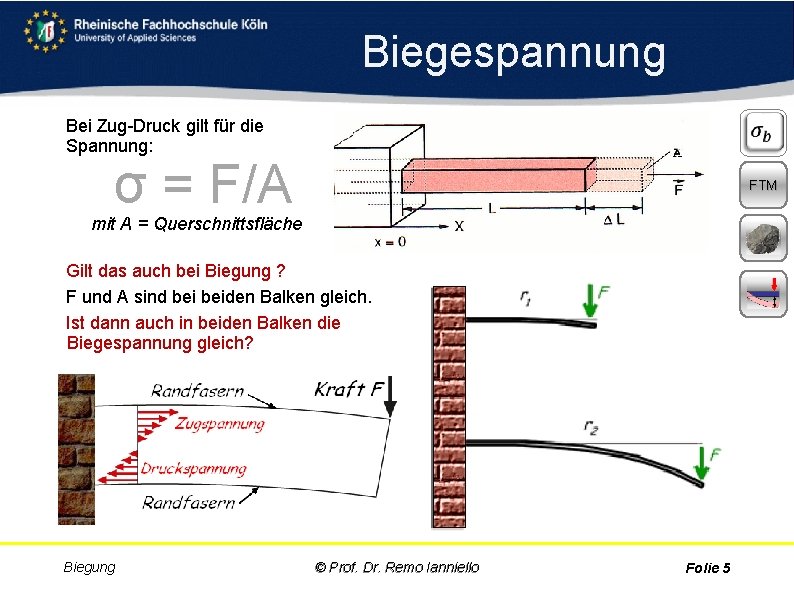
Biegespannung Bei Zug Druck gilt für die Spannung: σ = F/A FTM mit A = Querschnittsfläche Gilt das auch bei Biegung ? F und A sind beiden Balken gleich. Ist dann auch in beiden Balken die Biegespannung gleich? Biegung © Prof. Dr. Remo Ianniello Folie 5

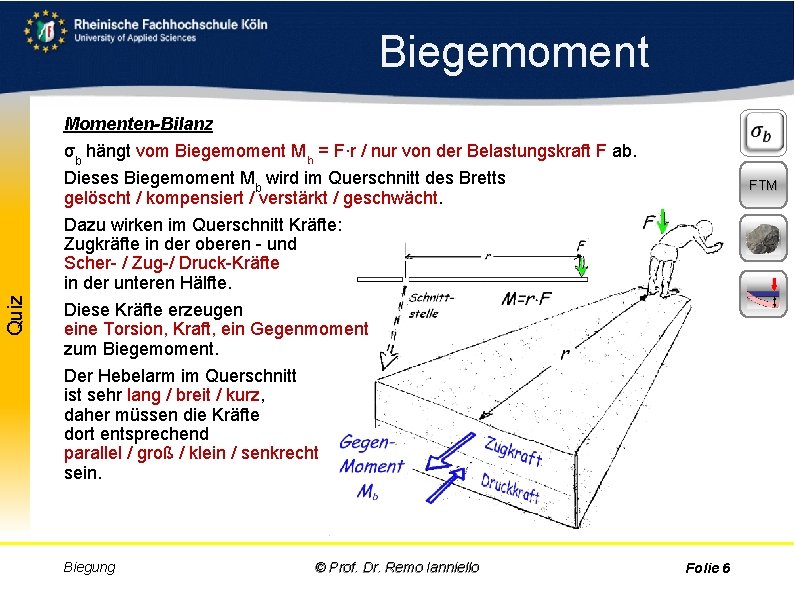
Aufgabe Quiz Biegemoment Momenten-Bilanz σb hängt vom Biegemoment Mb = F∙r / nur von der Belastungskraft F ab. Dieses Biegemoment Mb wird im Querschnitt des Bretts gelöscht / kompensiert / verstärkt / geschwächt. Dazu wirken im Querschnitt Kräfte: Zugkräfte in der oberen und Scher / Zug / Druck Kräfte in der unteren Hälfte. Diese Kräfte erzeugen eine Torsion, Kraft, ein Gegenmoment zum Biegemoment. Der Hebelarm im Querschnitt ist sehr lang / breit / kurz, daher müssen die Kräfte dort entsprechend parallel / groß / klein / senkrecht sein. Biegung © Prof. Dr. Remo Ianniello FTM Folie 6

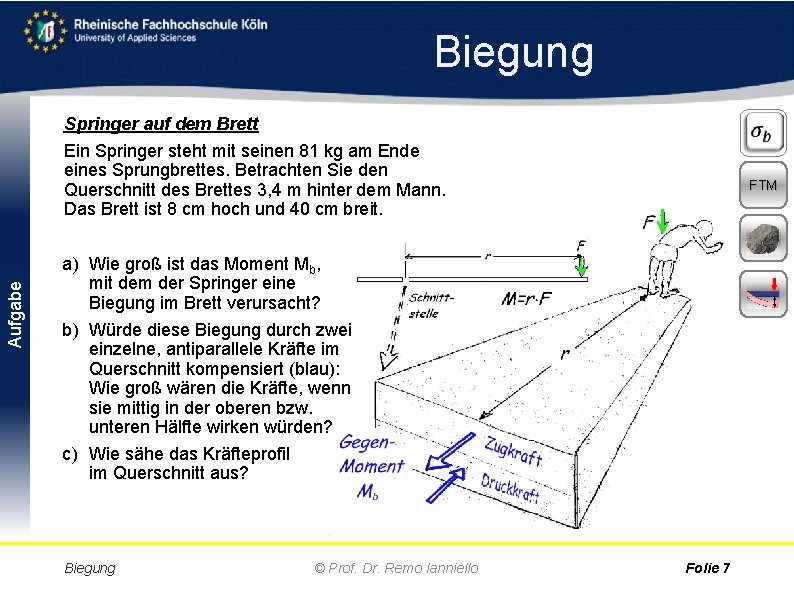
Biegung Aufgabe Springer auf dem Brett Ein Springer steht mit seinen 81 kg am Ende eines Sprungbrettes. Betrachten Sie den Querschnitt des Brettes 3, 4 m hinter dem Mann. Das Brett ist 8 cm hoch und 40 cm breit. FTM a) Wie groß ist das Moment Mb, mit dem der Springer eine Biegung im Brett verursacht? b) Würde diese Biegung durch zwei einzelne, antiparallele Kräfte im Querschnitt kompensiert (blau): Wie groß wären die Kräfte, wenn sie mittig in der oberen bzw. unteren Hälfte wirken würden? c) Wie sähe das Kräfteprofil im Querschnitt aus? Biegung © Prof. Dr. Remo Ianniello Folie 7

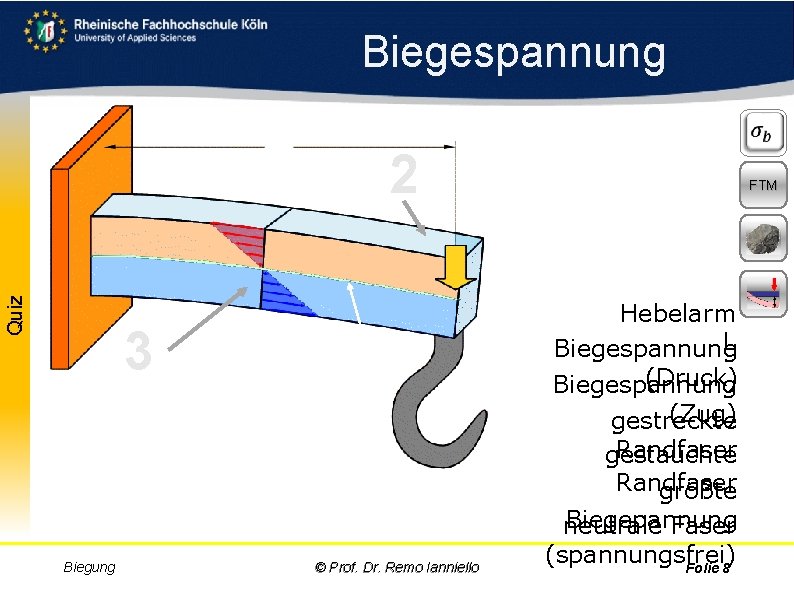
Biegespannung Aufgabe Quiz Hebelarm L 2 Randfaser größte Biegepannung Hebelarm L Biegespannung (Druck) Biegespannung 3 größte Biegepannung Biegespannung (Zug) gestreckte Randfaser gestauchte Randfaser größte (Druck) gestauchte Randfaser Biegung Biegespannung (Zug) gestreckte © Prof. Dr. Remo Ianniello Biegepannung neutrale Faser (spannungsfrei) Folie 8 FTM

Aufgabe Quiz Biegespannung Stützwirkung Obwohl sich Biegespannungen aus Zug und Druck Spannungen zusammen setzen, sind die zulässigen Spannungen für Biegung größer als die für Zug oder Druck. FTM Beispiel Einsatzstahl 18 Cr. Ni 8 Re = 785 N/mm 2 < b. F = 1. 100 N/mm 2 Wie ist dieser Unterschied zu erklären? Die Festigkeitswerte bei Biegebelastung sind infolge der Stützwirkung größer als bei Zug- bzw. Druck-Belastung Biegung © Prof. Dr. Remo Ianniello Folie 9

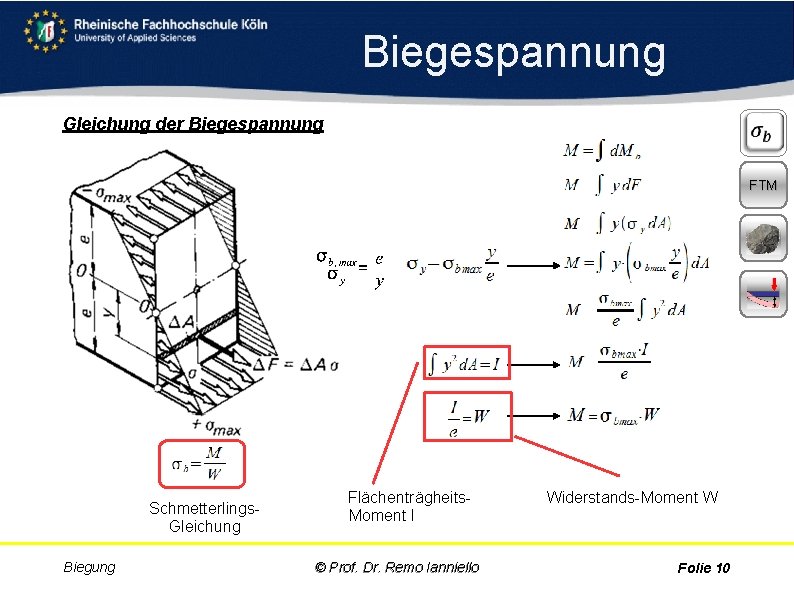
Biegespannung Gleichung der Biegespannung FTM Schmetterlings Gleichung Biegung Flächenträgheits Moment I © Prof. Dr. Remo Ianniello Widerstands Moment W Folie 10

Aufgabe Biegespannung Sprungbrett Ein stämmiger Herr steht am Ende eines Sprungbrettes, 4, 5 m von der Einspannung entfernt. Mit seinen 98 kg verbiegt er das Brett (W = 106 mm³) bis die Randfasern stark unter Biegespannung stehen. a) Wie groß ist diese Biegespannung? b) Wo tritt sie auf? c) Das Brett ist 40 cm breit und 10 cm dick. In welchem Abstand von der neutralen Faser ist die Spannung nur halb so groß? Biegung © Prof. Dr. Remo Ianniello FTM Folie 11

Flächenträgheits -Moment (FTM) Biegung © Prof. Dr. Remo Ianniello Folie 12

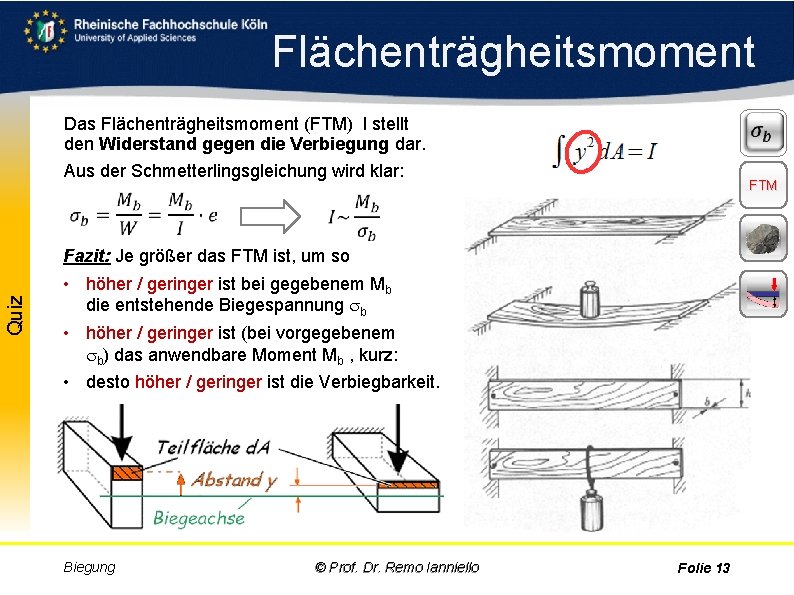
Flächenträgheitsmoment Das Flächenträgheitsmoment (FTM) I stellt den Widerstand gegen die Verbiegung dar. Aus der Schmetterlingsgleichung wird klar: FTM Aufgabe Quiz Fazit: Je größer das FTM ist, um so • höher / geringer ist bei gegebenem Mb die entstehende Biegespannung b • höher / geringer ist (bei vorgegebenem b) das anwendbare Moment Mb , kurz: • desto höher / geringer ist die Verbiegbarkeit. Biegung © Prof. Dr. Remo Ianniello Folie 13

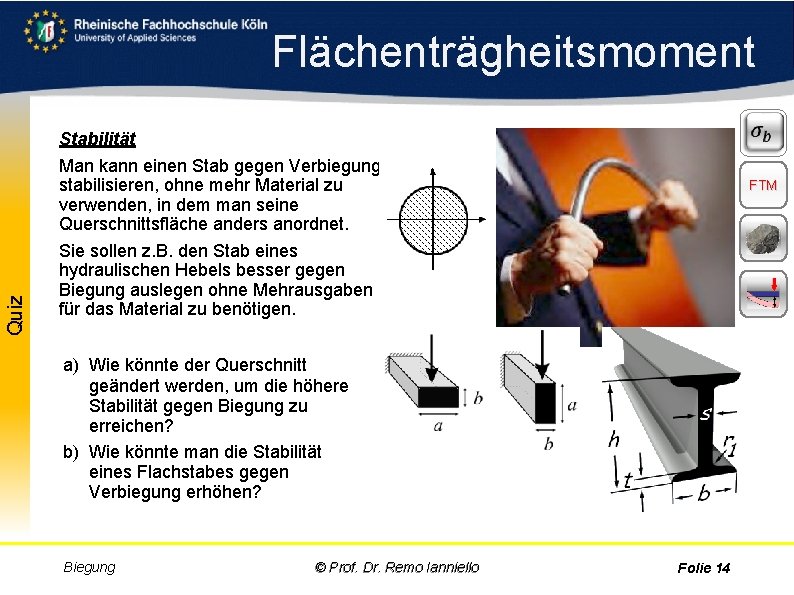
Aufgabe Quiz Flächenträgheitsmoment Stabilität Man kann einen Stab gegen Verbiegung stabilisieren, ohne mehr Material zu verwenden, in dem man seine Querschnittsfläche anders anordnet. Sie sollen z. B. den Stab eines hydraulischen Hebels besser gegen Biegung auslegen ohne Mehrausgaben für das Material zu benötigen. FTM a) Wie könnte der Querschnitt geändert werden, um die höhere Stabilität gegen Biegung zu erreichen? b) Wie könnte man die Stabilität eines Flachstabes gegen Verbiegung erhöhen? Biegung © Prof. Dr. Remo Ianniello Folie 14

Flächenträgheitsmoment Aufgabe Quiz Stabilität Man kann einen Stab gegen Verbiegung stabilisieren, ohne mehr Material zu verwenden, in dem man seine Querschnittsfläche anders anordnet. FTM a) Wie könnte man die Stabilität einer Container Wand erhöhen? b) Kennen Sie Beispiele aus der Praxis, bei denen die Oberflächengestaltung eine höhere Stabilität bewirkt? Biegung © Prof. Dr. Remo Ianniello Folie 15

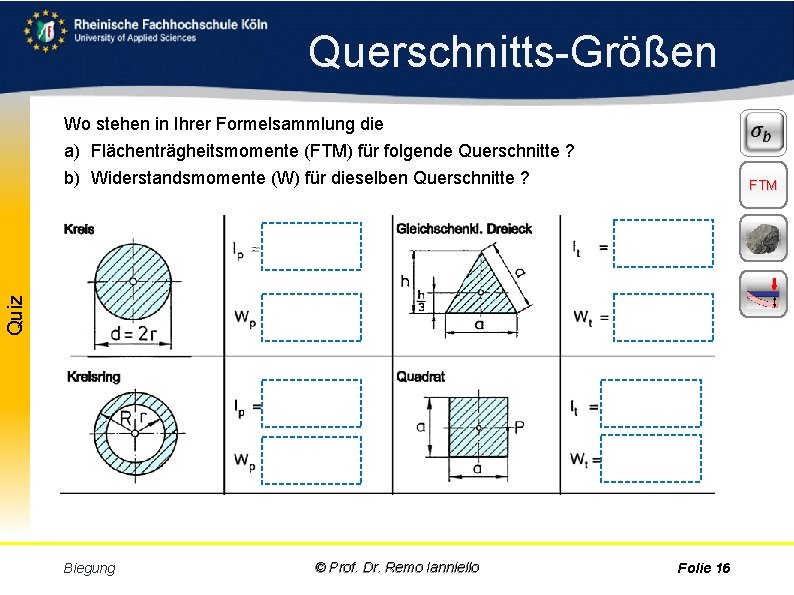
Querschnitts Größen Wo stehen in Ihrer Formelsammlung die a) Flächenträgheitsmomente (FTM) für folgende Querschnitte ? b) Widerstandsmomente (W) für dieselben Querschnitte ? Aufgabe Quiz FTM Biegung © Prof. Dr. Remo Ianniello Folie 16

Aufgabe Widerstandsmoment Achse Eine Achse aus Vergütungsstahl C 60 E mit d = 40 mm wird auf Biegung beansprucht. Die Sicherheitszahl ist hier v = 3 zu setzen. a) Wie groß ist das maximal erlaubte Biegemoment? b) Wie groß ist die Biegespannung in einer Faser, die von der Randfaser einen Abstand von 5 mm hat? Biegung © Prof. Dr. Remo Ianniello FTM Folie 17

Widerstandsmoment Welle Eine Welle aus S 185 mit d = 36 mm wird auf Biegung beansprucht. Die zulässige Biegespannung betrage b zul = 183 N/mm 2. FTM Aufgabe a) Wie groß ist das axiale Widerstandsmoment? b) Wie groß ist das maximal erlaubte Biegemoment? c) Wie erhält man bei bekanntem b max (= b zul) die Biegespannung von by in einer Faser, die von der Rand faser einen Abstand von 6 mm hat? Biegung © Prof. Dr. Remo Ianniello Folie 18

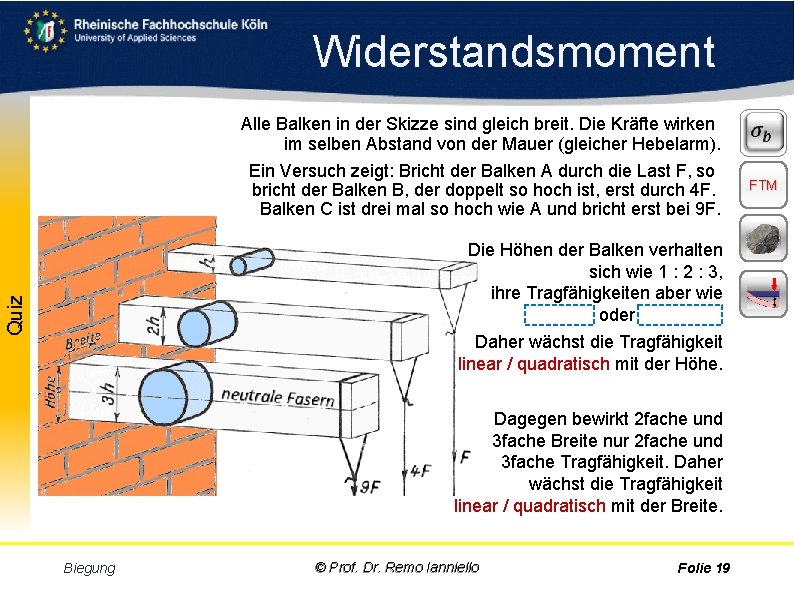
Widerstandsmoment Alle Balken in der Skizze sind gleich breit. Die Kräfte wirken im selben Abstand von der Mauer (gleicher Hebelarm). Ein Versuch zeigt: Bricht der Balken A durch die Last F, so bricht der Balken B, der doppelt so hoch ist, erst durch 4 F. Balken C ist drei mal so hoch wie A und bricht erst bei 9 F. Aufgabe Quiz Die Höhen der Balken verhalten sich wie 1 : 2 : 3, ihre Tragfähigkeiten aber wie 1 : 4 : 9 oder 1² : 2² : 3². Daher wächst die Tragfähigkeit linear / quadratisch mit der Höhe. Dagegen bewirkt 2 fache und 3 fache Breite nur 2 fache und 3 fache Tragfähigkeit. Daher wächst die Tragfähigkeit linear / quadratisch mit der Breite. Biegung © Prof. Dr. Remo Ianniello Folie 19 FTM

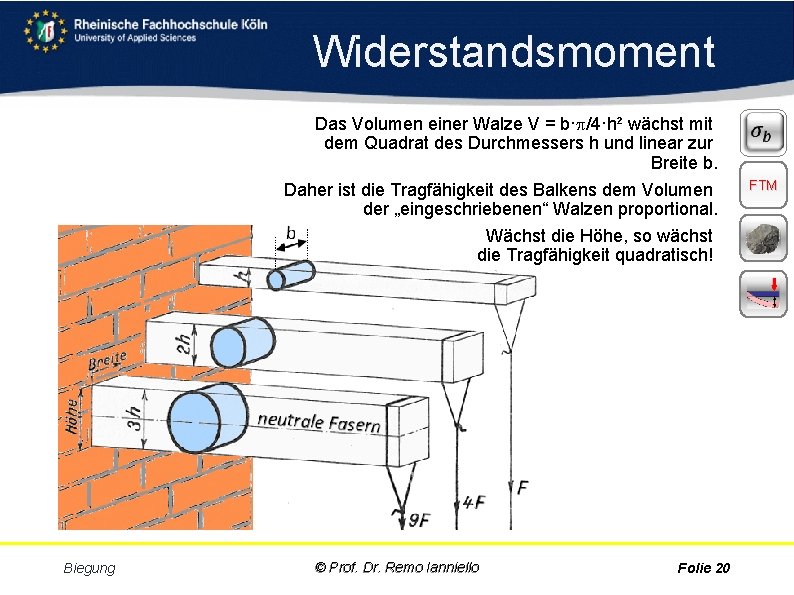
Widerstandsmoment Das Volumen einer Walze V = b· /4·h² wächst mit dem Quadrat des Durchmessers h und linear zur Breite b. Daher ist die Tragfähigkeit des Balkens dem Volumen der „eingeschriebenen“ Walzen proportional. Wächst die Höhe, so wächst die Tragfähigkeit quadratisch! Biegung © Prof. Dr. Remo Ianniello Folie 20 FTM

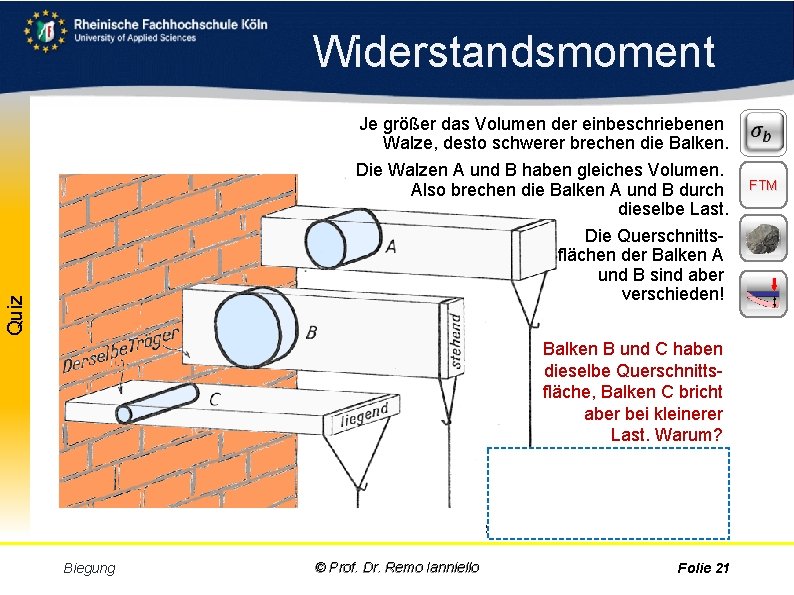
Widerstandsmoment Aufgabe Quiz Je größer das Volumen der einbeschriebenen Walze, desto schwerer brechen die Balken. Die Walzen A und B haben gleiches Volumen. Also brechen die Balken A und B durch dieselbe Last. Die Querschnitts flächen der Balken A und B sind aber verschieden! Balken B und C haben dieselbe Querschnitts fläche, Balken C bricht aber bei kleinerer Last. Warum? Weil das Volumen der Walze in C kleiner ist. Im selben Verhältnis hat sich seine Tragfähigkeit verringert. Biegung © Prof. Dr. Remo Ianniello Folie 21 FTM

Widerstandsmoment Flachstahl Aufgabe Ein Flachstahl aus E 335 mit den Abmessungen 25 mm 10 mm soll das Biegemoment Mb = 100 Nm aufnehmen. FTM a) Wie groß sind axiales Flächen und Widerstandsmoment, wenn der Flachstahl hochkant gebogen wird? b) Wie groß sind I und W, wenn der Flachstahl flachkant gebogen wird? Biegung © Prof. Dr. Remo Ianniello Folie 22

Fragen 1) Was unterscheidet die Biegespannung von der Zugspannung? Sie ist nicht von der Kraft pro Querschnitt abhängig. FTM Fragen 2) Wovon hängt das Widerstandsmoment ab? A) vom Werkstoff, B) vom E Modul, C) von der Querschnittsgeometrie, D) von der Biegespannung? C) von der Querschnittsgeometrie 3) Was ist die Bedeutung des axialen Flächenträgheitmoments I ? Widerstand gegen die Verbiegung. 4) Welche geometrische Größe ist für die Biegestabilität maßgebend? Der durchschnittliche Abstand der Querschnittsfläche von der Biegeachse (neutralen Faser), das FTM, das Widerstandsmoment 5) Wie berechnet man bei unsymmetrischen Querschnitten die Position der Biegeachse? Die Biegeachse verläuft immer durch den Schwerpunkt der Querschnittsfläche. Man bildet den gemeinsamen Schwerpunkt. 6) Wie hängen Randfaserabstand e, Widerstandsmoment W und lächenträgheitsmoment I miteinander zusammen? I = W·e Biegung © Prof. Dr. Remo Ianniello Folie 23

Satz von Steiner Biegung © Prof. Dr. Remo Ianniello Folie 24

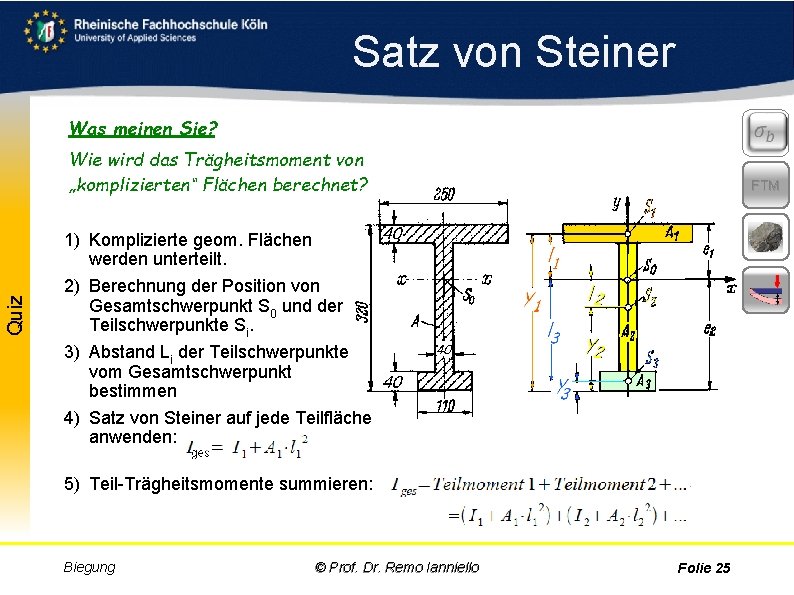
Aufgabe Quiz Satz von Steiner Was meinen Sie? Wie wird das Trägheitsmoment von „komplizierten“ Flächen berechnet? FTM 1) Komplizierte geom. Flächen werden unterteilt. 2) Berechnung der Position von Gesamtschwerpunkt S 0 und der Teilschwerpunkte Si. 3) Abstand Li der Teilschwerpunkte vom Gesamtschwerpunkt bestimmen 4) Satz von Steiner auf jede Teilfläche anwenden: 5) Teil Trägheitsmomente summieren: Biegung © Prof. Dr. Remo Ianniello Folie 25

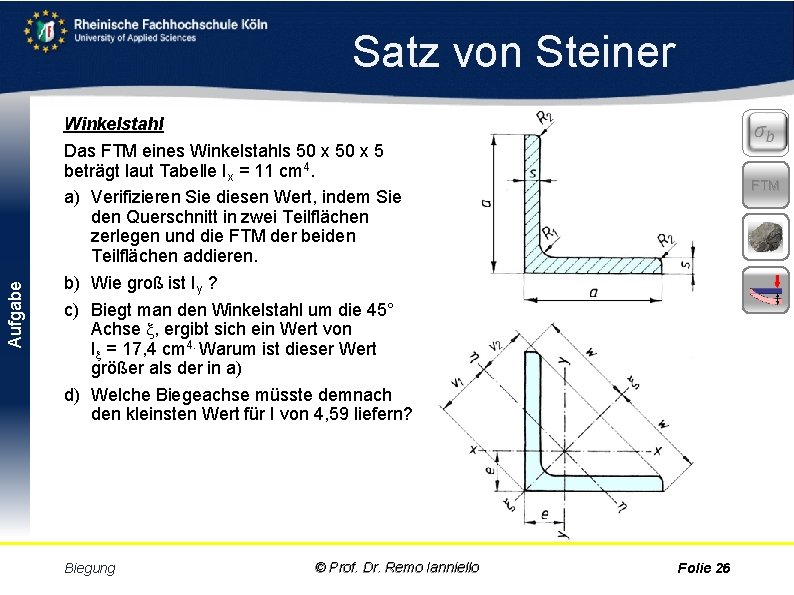
Aufgabe Satz von Steiner Winkelstahl Das FTM eines Winkelstahls 50 x 5 beträgt laut Tabelle Ix = 11 cm 4. a) Verifizieren Sie diesen Wert, indem Sie den Querschnitt in zwei Teilflächen zerlegen und die FTM der beiden Teilflächen addieren. b) Wie groß ist Iy ? c) Biegt man den Winkelstahl um die 45° Achse , ergibt sich ein Wert von I = 17, 4 cm 4. Warum ist dieser Wert größer als der in a) d) Welche Biegeachse müsste demnach den kleinsten Wert für I von 4, 59 liefern? Biegung © Prof. Dr. Remo Ianniello FTM Folie 26

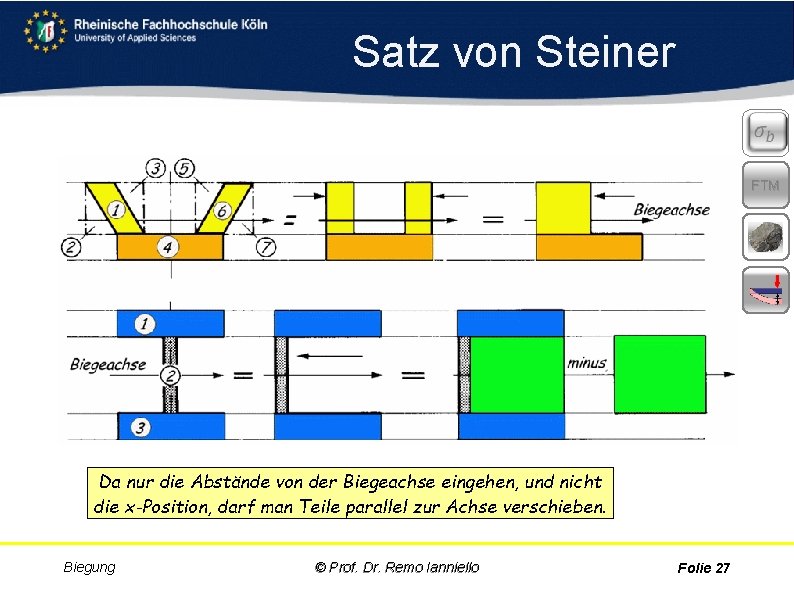
Satz von Steiner FTM Da nur die Abstände von der Biegeachse eingehen, und nicht die x-Position, darf man Teile parallel zur Achse verschieben. Biegung © Prof. Dr. Remo Ianniello Folie 27

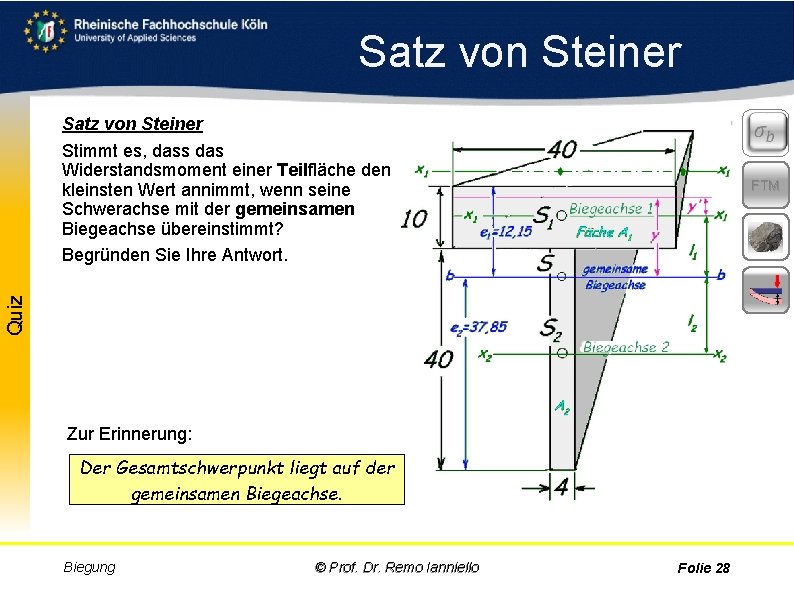
Satz von Steiner Stimmt es, dass das Widerstandsmoment einer Teilfläche den kleinsten Wert annimmt, wenn seine Schwerachse mit der gemeinsamen Biegeachse übereinstimmt? Begründen Sie Ihre Antwort. Aufgabe Quiz FTM Zur Erinnerung: Der Gesamtschwerpunkt liegt auf der gemeinsamen Biegeachse. Biegung © Prof. Dr. Remo Ianniello Folie 28

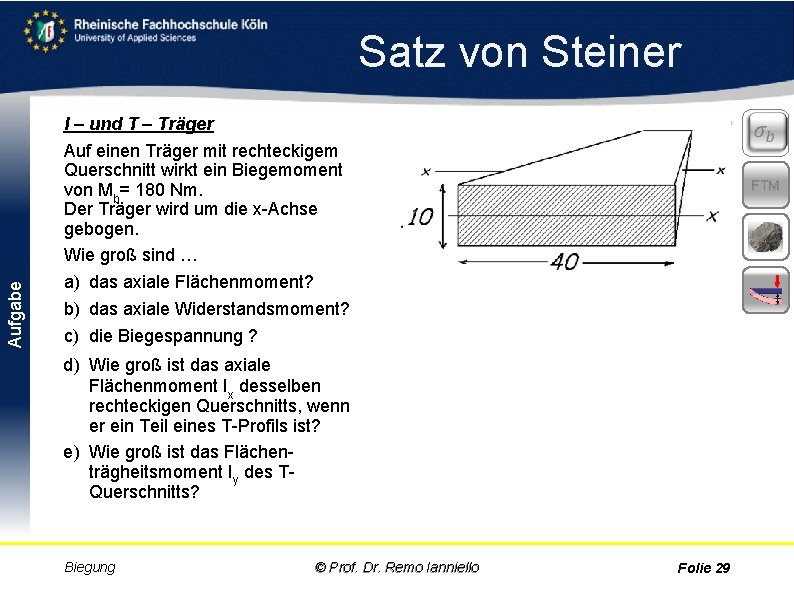
Aufgabe Satz von Steiner I – und T – Träger Auf einen Träger mit rechteckigem Querschnitt wirkt ein Biegemoment von Mb= 180 Nm. Der Träger wird um die x Achse gebogen. Wie groß sind … a) das axiale Flächenmoment? b) das axiale Widerstandsmoment? c) die Biegespannung ? FTM d) Wie groß ist das axiale Flächenmoment Ix desselben rechteckigen Querschnitts, wenn er ein Teil eines T Profils ist? e) Wie groß ist das Flächen trägheitsmoment Iy des T Querschnitts? Biegung © Prof. Dr. Remo Ianniello Folie 29

Durchbiegung Biegung © Prof. Dr. Remo Ianniello Folie 30

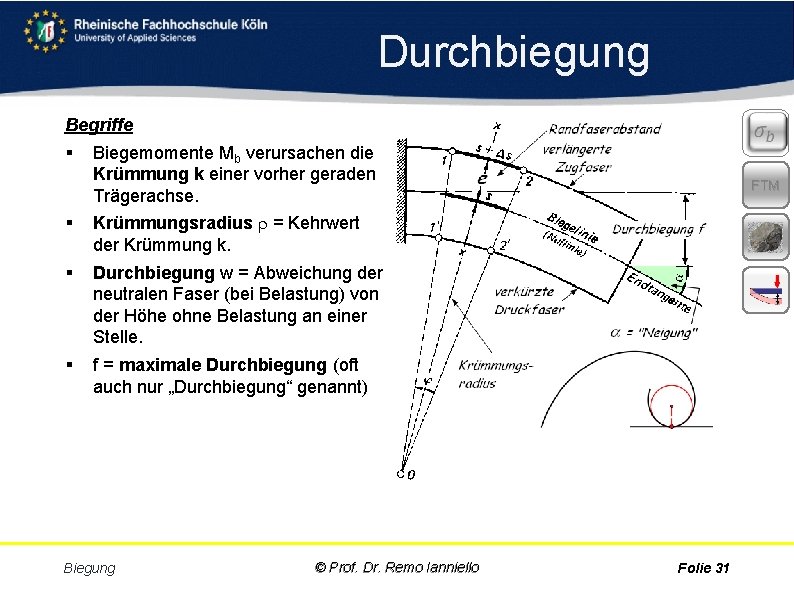
Durchbiegung Begriffe § Biegemomente Mb verursachen die Krümmung k einer vorher geraden Trägerachse. § Krümmungsradius = Kehrwert der Krümmung k. § Durchbiegung w = Abweichung der neutralen Faser (bei Belastung) von der Höhe ohne Belastung an einer Stelle. § f = maximale Durchbiegung (oft auch nur „Durchbiegung“ genannt) Biegung © Prof. Dr. Remo Ianniello FTM Folie 31

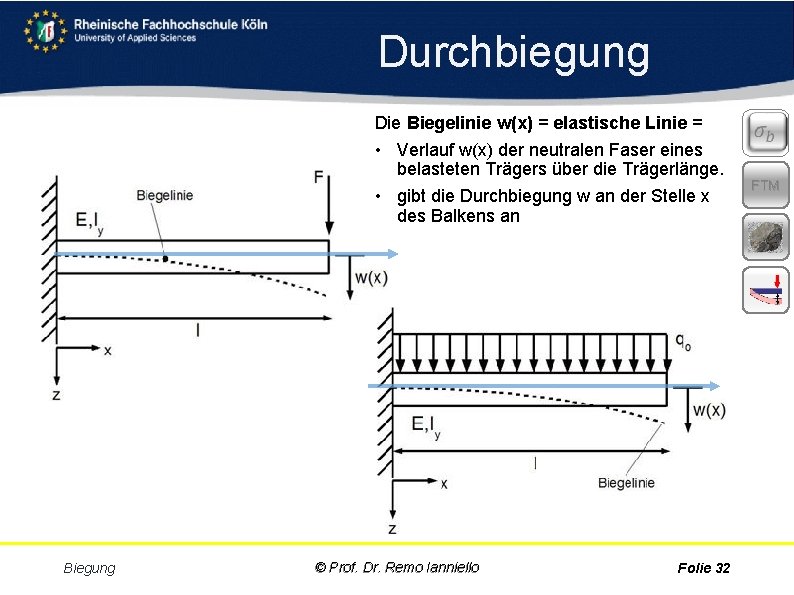
Durchbiegung Die Biegelinie w(x) = elastische Linie = • Verlauf w(x) der neutralen Faser eines belasteten Trägers über die Trägerlänge. • gibt die Durchbiegung w an der Stelle x des Balkens an Biegung © Prof. Dr. Remo Ianniello Folie 32 FTM

Durchbiegung Je größer das Biegemoment Mb, desto so • stärker wird der Träger gekrümmt (k groß) • kleiner wird der Krümmungsradius . Je weniger elastisch ein Werkstoff (E-Modul groß), desto • kleiner die Krümmung, • größer der Krümmungsradius FTM + E + Je starrer sich ein Träger gegen Biegung verhält, desto • größer das Flächenträgheitsmoment I • kleiner die Krümmung. Daraus ergibt sich folgender Zusammenhang: Biegung © Prof. Dr. Remo Ianniello I = Folie 33

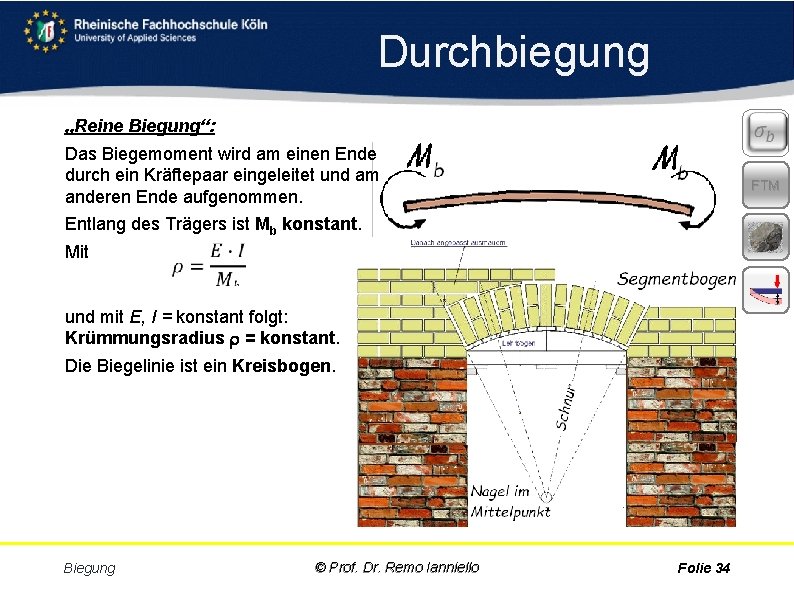
Durchbiegung „Reine Biegung“: Das Biegemoment wird am einen Ende durch ein Kräftepaar eingeleitet und am anderen Ende aufgenommen. FTM Entlang des Trägers ist Mb konstant. Mit und mit E, I = konstant folgt: Krümmungsradius = konstant. Die Biegelinie ist ein Kreisbogen. Biegung © Prof. Dr. Remo Ianniello Folie 34

Durchbiegung Biegemoment ist nicht konstant Durchbiegung w(x) kann bei best. x. E zu hoch werden FTM Zu hohe Durchbiegung w(x) kann z. Bruch führen Aufgabe: max. Durch biegung f = wmax ermitteln f mit fzul vergleichen Bei Bedarf: Bauteil verstärken; Verkehrslast einschränken Biegung © Prof. Dr. Remo Ianniello Folie 35

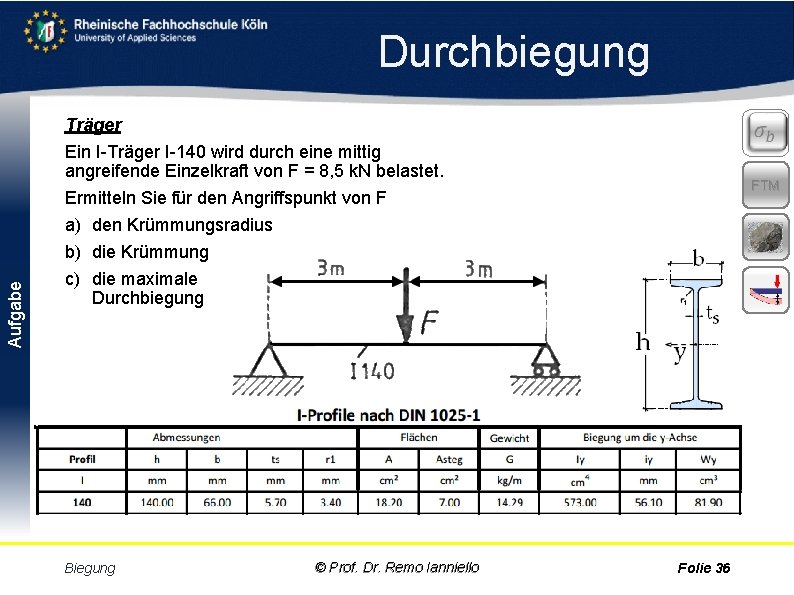
Aufgabe Durchbiegung Träger Ein I Träger I 140 wird durch eine mittig angreifende Einzelkraft von F = 8, 5 k. N belastet. Ermitteln Sie für den Angriffspunkt von F a) den Krümmungsradius b) die Krümmung c) die maximale Durchbiegung Biegung © Prof. Dr. Remo Ianniello FTM Folie 36

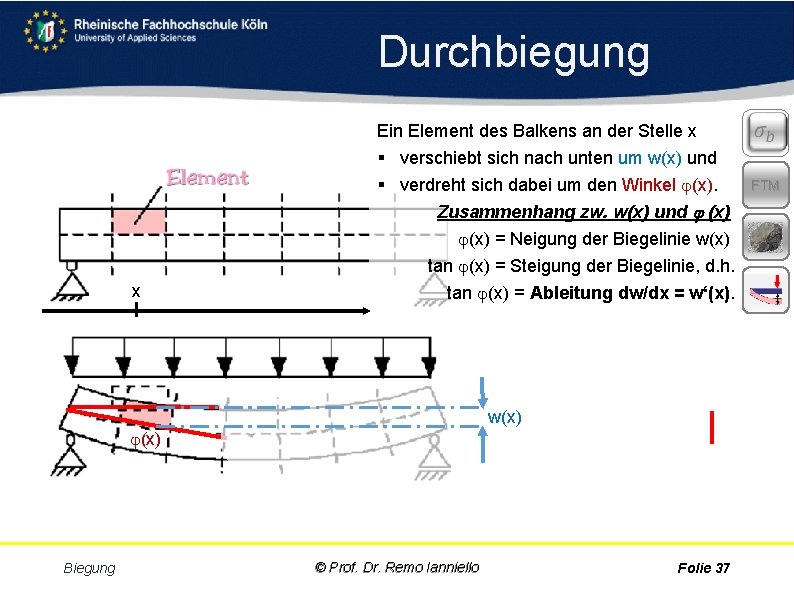
Durchbiegung x Ein Element des Balkens an der Stelle x § verschiebt sich nach unten um w(x) und FTM § verdreht sich dabei um den Winkel (x). Zusammenhang zw. w(x) und (x) = Neigung der Biegelinie w(x) tan (x) = Steigung der Biegelinie, d. h. tan (x) = Ableitung dw/dx = w‘(x). w(x) Biegung © Prof. Dr. Remo Ianniello Folie 37

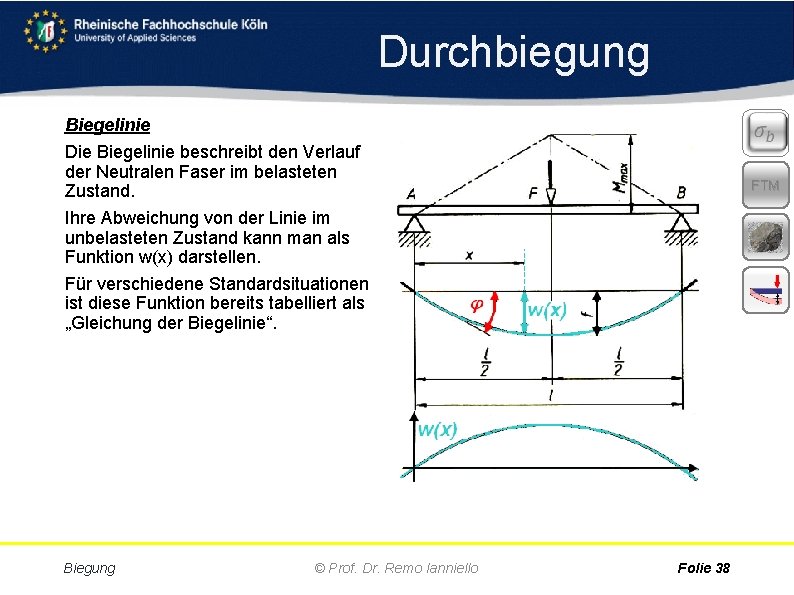
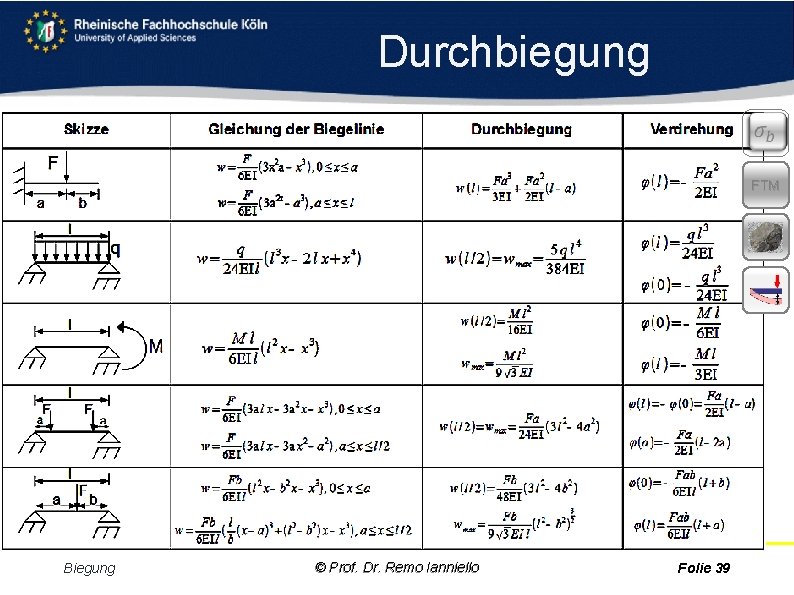
Durchbiegung Biegelinie Die Biegelinie beschreibt den Verlauf der Neutralen Faser im belasteten Zustand. Ihre Abweichung von der Linie im unbelasteten Zustand kann man als Funktion w(x) darstellen. Für verschiedene Standardsituationen ist diese Funktion bereits tabelliert als „Gleichung der Biegelinie“. Biegung © Prof. Dr. Remo Ianniello FTM Folie 38

Durchbiegung FTM Biegung © Prof. Dr. Remo Ianniello Folie 39

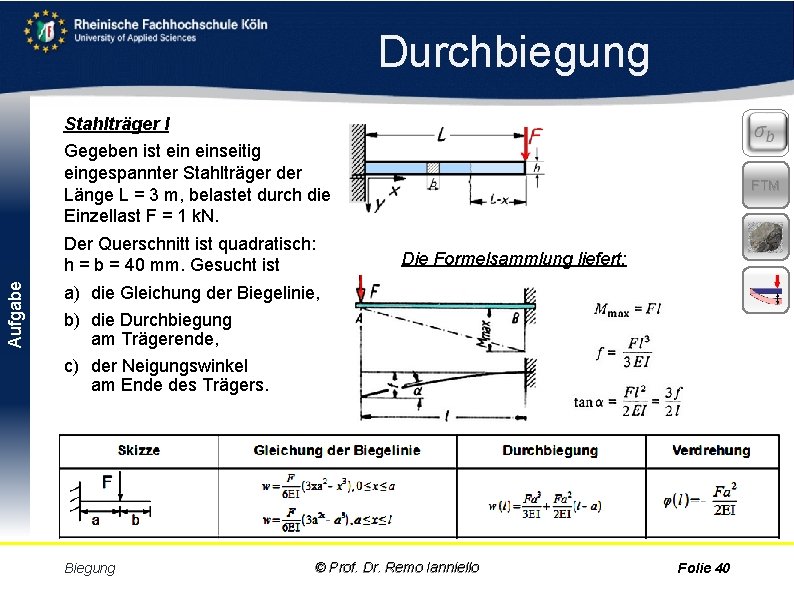
Durchbiegung Stahlträger I Gegeben ist einseitig eingespannter Stahlträger der Länge L = 3 m, belastet durch die Einzellast F = 1 k. N. FTM Aufgabe Der Querschnitt ist quadratisch: h = b = 40 mm. Gesucht ist Die Formelsammlung liefert: a) die Gleichung der Biegelinie, b) die Durchbiegung am Trägerende, c) der Neigungswinkel am Ende des Trägers. Biegung © Prof. Dr. Remo Ianniello Folie 40

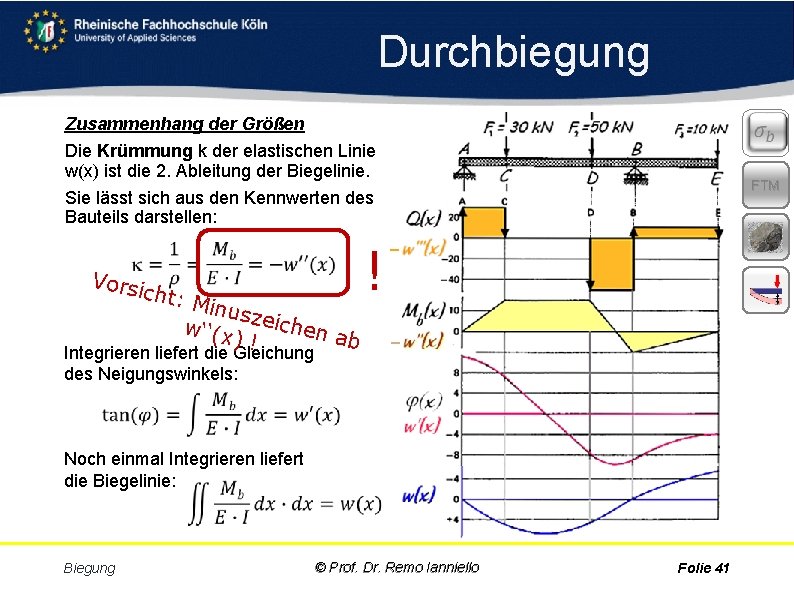
Durchbiegung Zusammenhang der Größen Die Krümmung k der elastischen Linie w(x) ist die 2. Ableitung der Biegelinie. Sie lässt sich aus den Kennwerten des Bauteils darstellen: Vors icht: Minu s w‘‘(x zeichen a )! b FTM ! Integrieren liefert die Gleichung des Neigungswinkels: Noch einmal Integrieren liefert die Biegelinie: Biegung © Prof. Dr. Remo Ianniello Folie 41

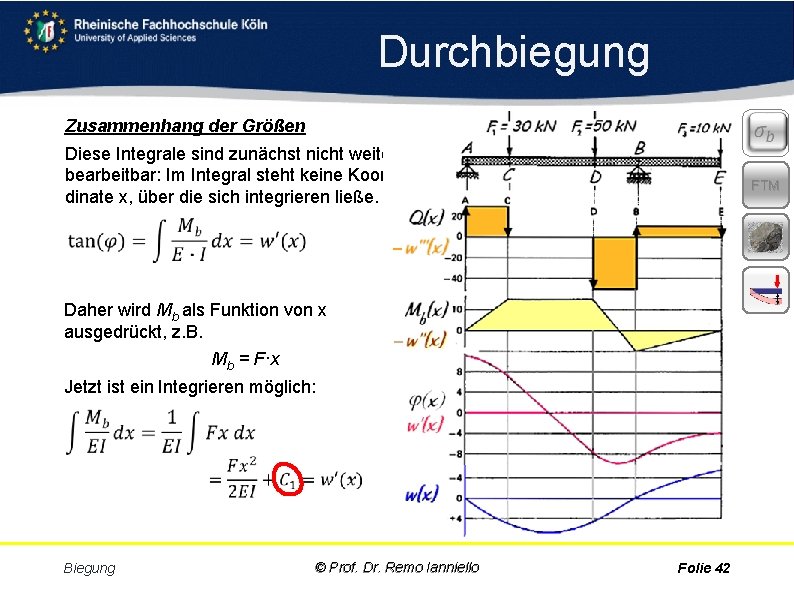
Durchbiegung Zusammenhang der Größen Diese Integrale sind zunächst nicht weiter bearbeitbar: Im Integral steht keine Koor dinate x, über die sich integrieren ließe. FTM Daher wird Mb als Funktion von x ausgedrückt, z. B. Mb = F·x Jetzt ist ein Integrieren möglich: Biegung © Prof. Dr. Remo Ianniello Folie 42

Durchbiegung Randbedingungen Erstellt man die Gleichung der Biege linie selbt, muss man Integrale lösen. Man erhält dabei eine Integrationskonstante. Diese Konstante lässt sich mit Hilfe von Randbedingungen lösen, die sich aus der Lagerung des Trägers ergeben: Biegung © Prof. Dr. Remo Ianniello FTM Folie 43

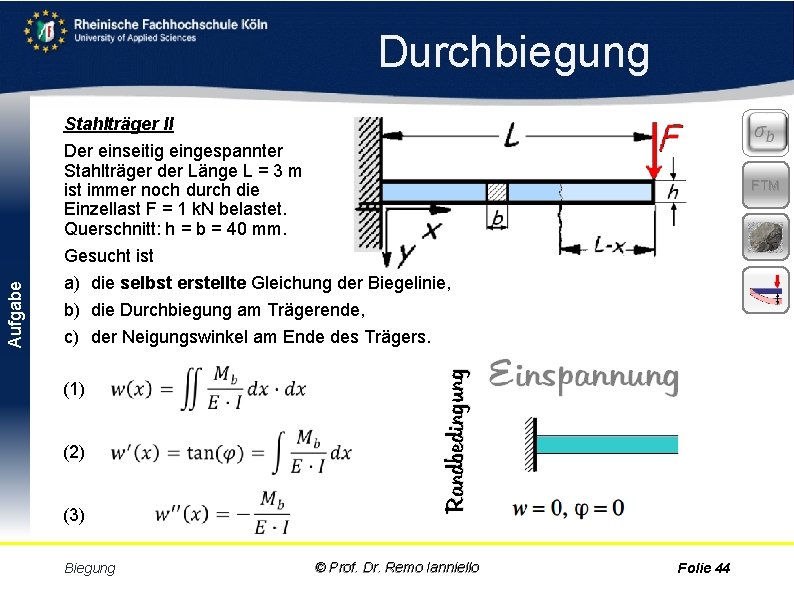
Stahlträger II Der einseitig eingespannter Stahlträger der Länge L = 3 m ist immer noch durch die Einzellast F = 1 k. N belastet. Querschnitt: h = b = 40 mm. Gesucht ist a) die selbst erstellte Gleichung der Biegelinie, b) die Durchbiegung am Trägerende, c) der Neigungswinkel am Ende des Trägers. (1) (2) (3) Biegung FTM Randbedingung Aufgabe Durchbiegung © Prof. Dr. Remo Ianniello Folie 44

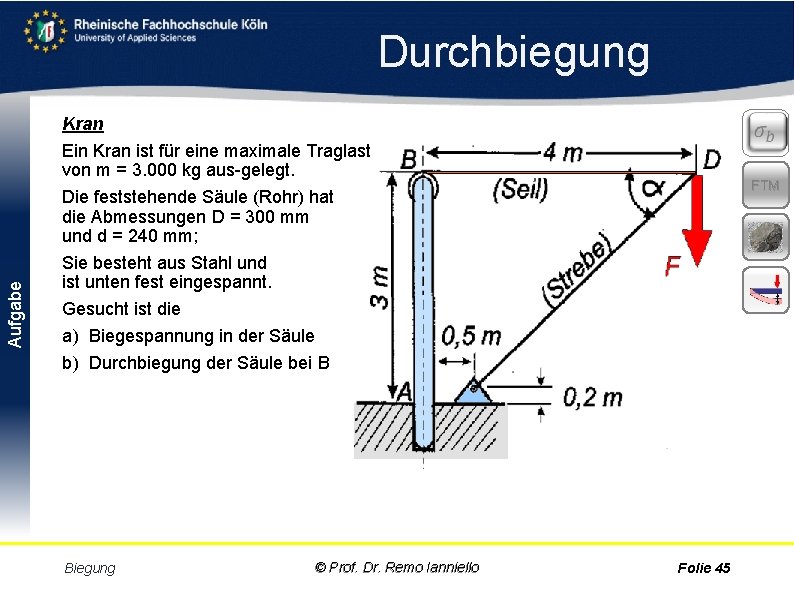
Aufgabe Durchbiegung Kran Ein Kran ist für eine maximale Traglast von m = 3. 000 kg aus gelegt. Die feststehende Säule (Rohr) hat die Abmessungen D = 300 mm und d = 240 mm; Sie besteht aus Stahl und ist unten fest eingespannt. Gesucht ist die a) Biegespannung in der Säule b) Durchbiegung der Säule bei B Biegung © Prof. Dr. Remo Ianniello FTM Folie 45

Übungs Aufgaben Biegung © Prof. Dr. Remo Ianniello Folie 46

FTM Aufgabe Winkelstahl Das FTM eines Hohlprofils 50 x 30 mm² und der Wanddicke s = 3 mm beträgt laut Tabelle Ix = 13, 6 cm 4. Verifizieren Sie diesen Wert, indem Sie den Querschnitt in zwei. Teilflächen zerlegen und die FTM der Teilflächen voneinander subtrahieren. Biegung © Prof. Dr. Remo Ianniello Folie 47

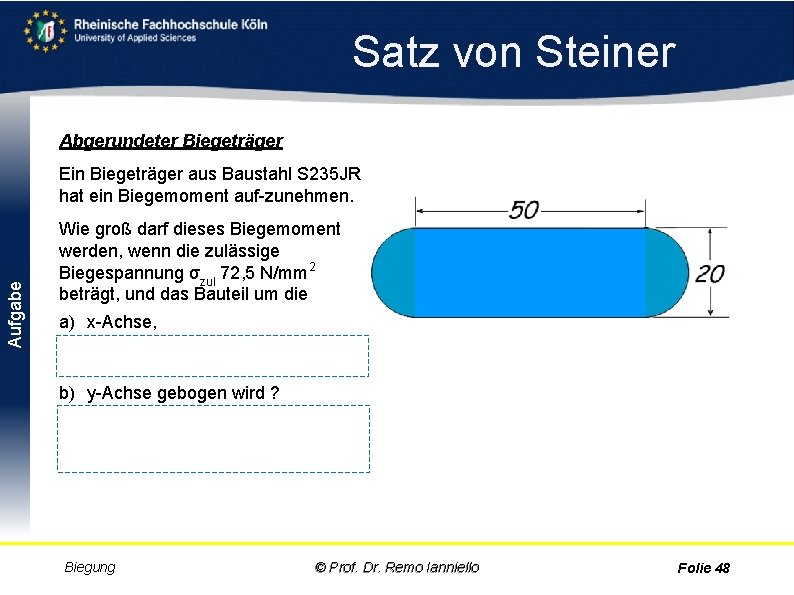
Satz von Steiner Abgerundeter Biegeträger Aufgabe Ein Biegeträger aus Baustahl S 235 JR hat ein Biegemoment auf zunehmen. Wie groß darf dieses Biegemoment werden, wenn die zulässige Biegespannung σzul 72, 5 N/mm 2 beträgt, und das Bauteil um die a) x Achse, I 1 = 7. 854 mm 4, I 2 = 33. 333 mm 4, Mb max = 298, 5 Nm b) y Achse gebogen wird ? I 1 = 135, 42 10³ mm 4, I 2 = 208, 3 10³ mm 4, Mb max = 992, 52 Nm Biegung © Prof. Dr. Remo Ianniello Folie 48

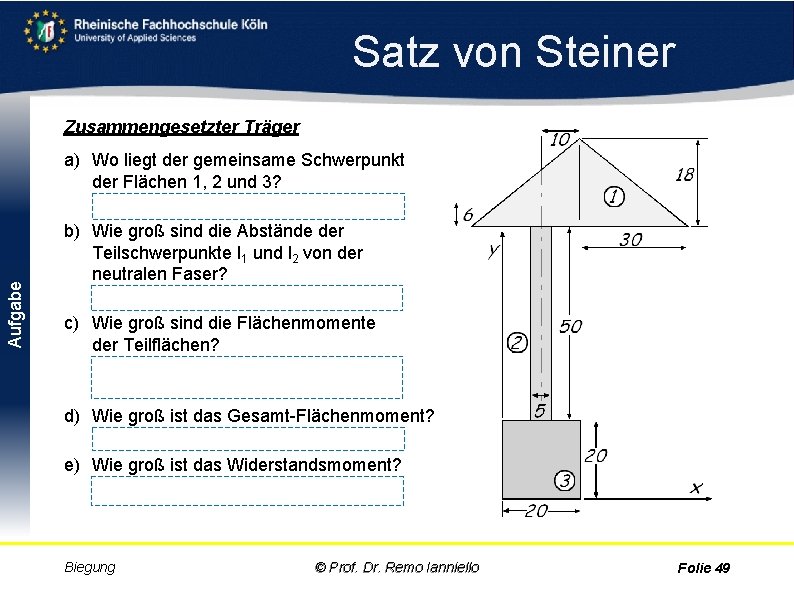
Satz von Steiner Aufgabe Zusammengesetzter Träger a) Wo liegt der gemeinsame Schwerpunkt der Flächen 1, 2 und 3? Ergebnis: S=(14, 53 mm / 47, 3 mm) b) Wie groß sind die Abstände der Teilschwerpunkte l 1 und l 2 von der neutralen Faser? l 1 = 28, 7 mm, l 2=2, 3 mm, l 3=37, 3 mm c) Wie groß sind die Flächenmomente der Teilflächen? I 1 = 454. 512, 6 mm 4, I 2 = 53. 405, 8 mm 4, I 3 = 569. 849 mm 4 d) Wie groß ist das Gesamt Flächenmoment? Iges= 1, 08 106 mm 4 e) Wie groß ist das Widerstandsmoment? W = 22. 750 mm³ Biegung © Prof. Dr. Remo Ianniello Folie 49

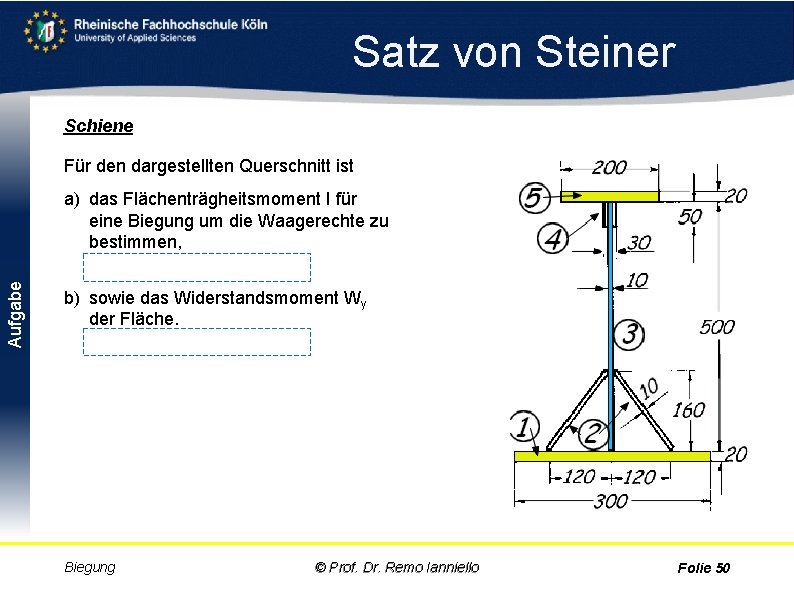
Satz von Steiner Schiene Für den dargestellten Querschnitt ist Aufgabe a) das Flächenträgheitsmoment I für eine Biegung um die Waagerechte zu bestimmen, Ix = 907, 939· 106 mm 4 b) sowie das Widerstandsmoment Wy der Fläche. Wy = 517, 867· 103 mm 3 Biegung © Prof. Dr. Remo Ianniello Folie 50

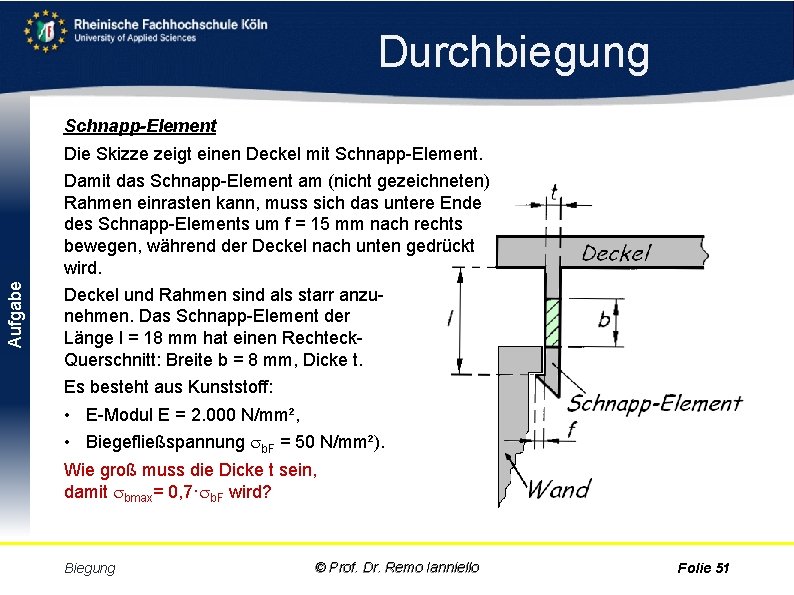
Durchbiegung Schnapp-Element Die Skizze zeigt einen Deckel mit Schnapp Element. Aufgabe Damit das Schnapp Element am (nicht gezeichneten) Rahmen einrasten kann, muss sich das untere Ende des Schnapp Elements um f = 15 mm nach rechts bewegen, während der Deckel nach unten gedrückt wird. Deckel und Rahmen sind als starr anzu nehmen. Das Schnapp Element der Länge l = 18 mm hat einen Rechteck Querschnitt: Breite b = 8 mm, Dicke t. Es besteht aus Kunststoff: • E Modul E = 2. 000 N/mm², • Biegefließspannung b. F = 50 N/mm²). Wie groß muss die Dicke t sein, damit bmax= 0, 7· b. F wird? Biegung © Prof. Dr. Remo Ianniello Folie 51

Aufgabe Lösung Durchbiegung Biegung © Prof. Dr. Remo Ianniello Folie 52

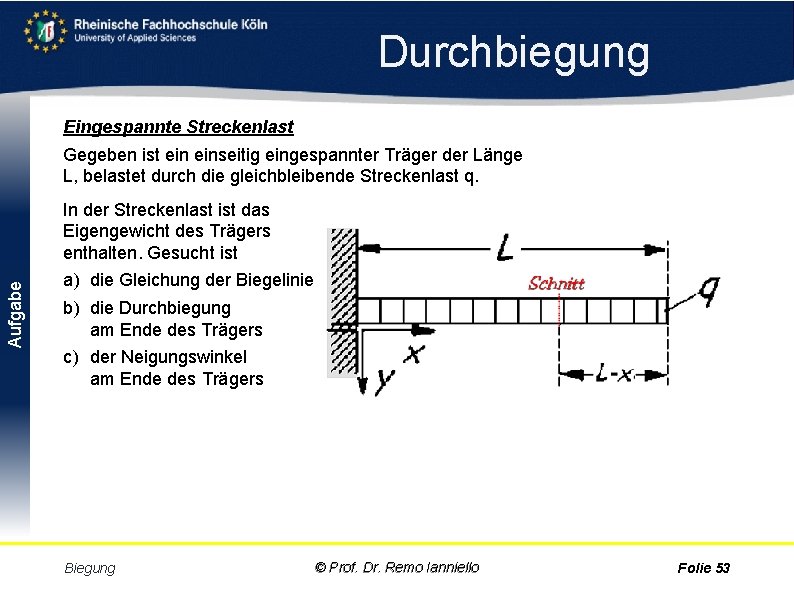
Durchbiegung Eingespannte Streckenlast Gegeben ist einseitig eingespannter Träger der Länge L, belastet durch die gleichbleibende Streckenlast q. Aufgabe In der Streckenlast ist das Eigengewicht des Trägers enthalten. Gesucht ist a) die Gleichung der Biegelinie b) die Durchbiegung am Ende des Trägers c) der Neigungswinkel am Ende des Trägers Biegung © Prof. Dr. Remo Ianniello Folie 53

Aufgabe Lösung Durchbiegung Biegung © Prof. Dr. Remo Ianniello Folie 54

Aufgabe Durchbiegung Freiträger Ein Freiträger vom Profil I 160 ist mit einer Streckenlast von fq = 179 N/m (Gewichts kraft) belastet. Länge l = 4 m, F = 900 N, E = 2, 1 105 N/mm² Berechnen Sie die Durchbiegung am freien Ende, hervorgerufen nur durch die Streckenlast, wenn die y Achse des Querschnittes senkrecht steht. Welche Durchbiegung tritt auf, wenn statt der Streckenlast am freien Ende in der y Richtung nur die Kraft F angreift? Wie groß ist die Durchbiegung, hervorgerufen durch Streckenlast q und Kraft F, wenn der Träger mit waagerechter y Achse befestigt wird? Welche Stützkräfte sind in beiden Trägerlagen (horizontal und vertikal) am freien Ende erforderlich, damit der Träger an dieser Stelle keine Durchbiegung hat? a) f 1 = 2, 917 mm, b) f 2 = 9, 778 mm c) f = 217 mm d) Fx = 1. 168 N = Fy Biegung © Prof. Dr. Remo Ianniello Folie 55

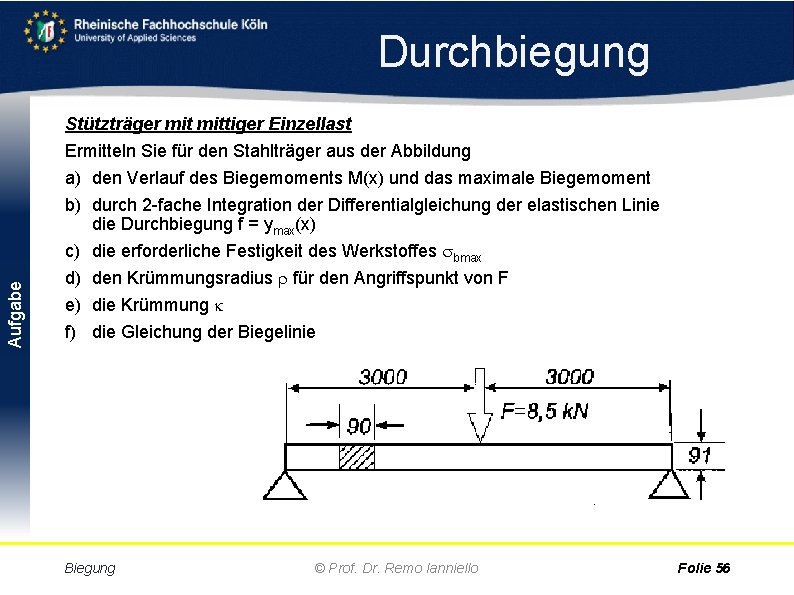
Aufgabe Durchbiegung Stützträger mittiger Einzellast Ermitteln Sie für den Stahlträger aus der Abbildung a) den Verlauf des Biegemoments M(x) und das maximale Biegemoment b) durch 2 fache Integration der Differentialgleichung der elastischen Linie die Durchbiegung f = ymax(x) c) die erforderliche Festigkeit des Werkstoffes bmax d) den Krümmungsradius für den Angriffspunkt von F e) die Krümmung f) die Gleichung der Biegelinie Biegung © Prof. Dr. Remo Ianniello Folie 56

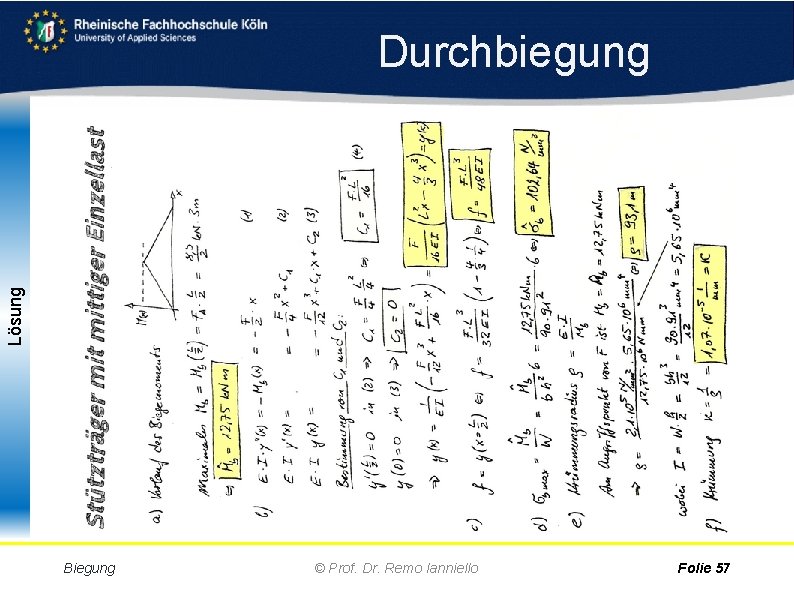
Aufgabe Lösung Durchbiegung Biegung © Prof. Dr. Remo Ianniello Folie 57

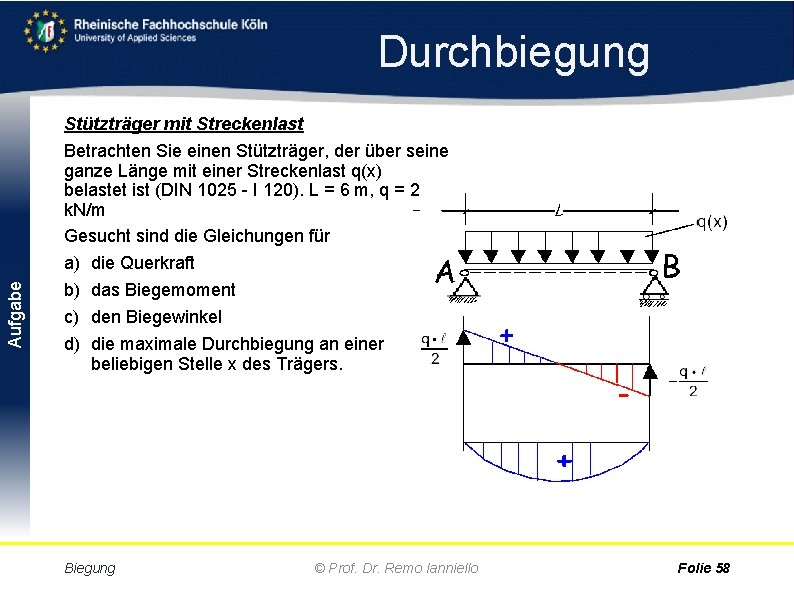
Aufgabe Durchbiegung Stützträger mit Streckenlast Betrachten Sie einen Stützträger, der über seine ganze Länge mit einer Streckenlast q(x) belastet ist (DIN 1025 I 120). L = 6 m, q = 2 k. N/m Gesucht sind die Gleichungen für a) die Querkraft b) das Biegemoment c) den Biegewinkel d) die maximale Durchbiegung an einer beliebigen Stelle x des Trägers. Biegung © Prof. Dr. Remo Ianniello Folie 58

Aufgabe Lösung Durchbiegung Biegung © Prof. Dr. Remo Ianniello Folie 59

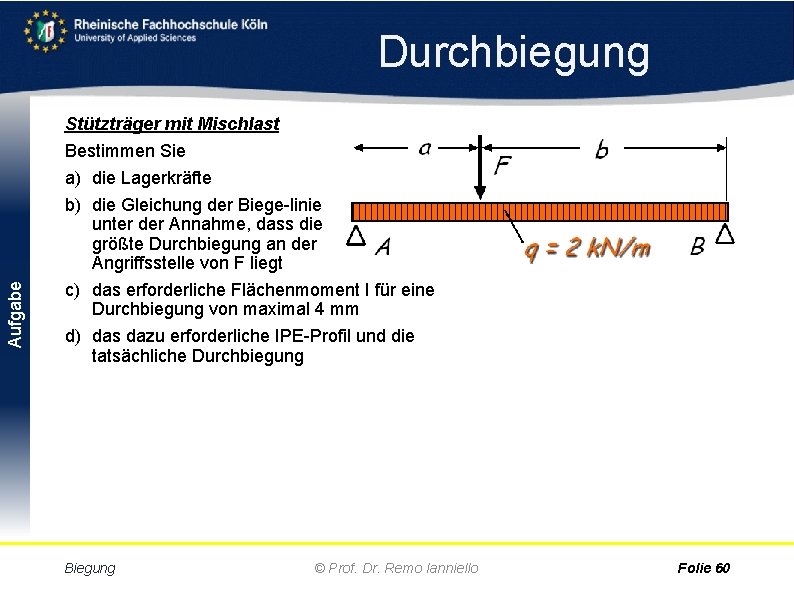
Aufgabe Durchbiegung Stützträger mit Mischlast Bestimmen Sie a) die Lagerkräfte b) die Gleichung der Biege linie unter der Annahme, dass die größte Durchbiegung an der Angriffsstelle von F liegt c) das erforderliche Flächenmoment I für eine Durchbiegung von maximal 4 mm d) das dazu erforderliche IPE Profil und die tatsächliche Durchbiegung Biegung © Prof. Dr. Remo Ianniello Folie 60