BiDecomposition of Discrete Function Sets Bernd Steinbach Christian

Bi-Decomposition of Discrete Function Sets Bernd Steinbach *, Christian Lang *, and Marek A. Perkowski + * Freiberg University of Mining and Technology Institute of Computer Science, Freiberg (Sachs. ), Germany + Portland State University, Department of Electrical and Computer Engineering, Portland (Oregon), USA 1

Outline • • Introduction Function Sets Bi-Decomposition Strategy EXOR-Decomposition of Function Sets Results Conclusion 2

Introduction • Incompletely specified functions (ISFs) are a generalization of Boolean functions. • There are many multi-stage design algorithms for ISFs. • We propose function sets as a generalization of ISFs to improve many of these design algorithms. • We demonstrate our method on the example of EXOR-bi-decomposition. 3

Function Sets I • There are two ways to interpret ISFs: – incompletely specified function – set of 2 s fully specified functions, s = number of don’t cares • Example: F = {f 1, f 2, f 3, f 4} b F(a, b) 0 1 a 0 1 F 0 f 1(a, b) f 2(a, b) f 3(a, b) f 4(a, b) 1 0 1 1 0 0 0 4

Function Sets II • The functions of an ISF and the AND and OR operation form a lattice, a special type of Boolean algebra • If f 1, f 2 Î F, then f 1 Ù f 2 Î F and f 1 Ú f 2 Î F • Example: f 3 Ù f 4 = f 1 Î F, and f 3 Ú f 4 = f 2 Î F b F(a, b) 0 1 a 0 1 F 0 f 1(a, b) f 2(a, b) f 3(a, b) f 4(a, b) 1 0 1 1 0 0 0 5

Function Sets III • There are function sets that are lattices, but not ISFs: R={f 1, f 2} ¹ F = {f 1, f 2, f 3, f 4} • There are function sets that are not lattices: S={f 3, f 4}, f 3 Ù f 4 = f 1 Ï S R={f 1, f 2} b F(a, b) 0 1 a 0 1 F 0 S={f 3, f 4} f 1(a, b) f 2(a, b) f 3(a, b) f 4(a, b) 1 0 0 0 1 1 1 0 1 0 0 0 6

Bi-Decomposition for Binary Circuits Structure A C B g(A, C) o f(A, B, C) h(B, C) f(A, B, C) = g(A, C) Ú h(B, C) f(A, B, C) = g(A, C) Ù h(B, C) f(A, B, C) = g(A, C) Å h(B, C) ORBi-Decomposition ANDBi-Decomposition EXORBi-Decomposition 7

Decomposition Strategy I • An ISF F(A, B, C) is bi-decomposed into function sets G(A, C) and H(B, C) • This decomposition is recursively repeated. • More functions in G(A, C) means fewer functions in H(B, C) and vice versa. • Our strategy: Include into G(A, C) as many functions as possible, design G(A, C), then make the same with H(B, C). 8

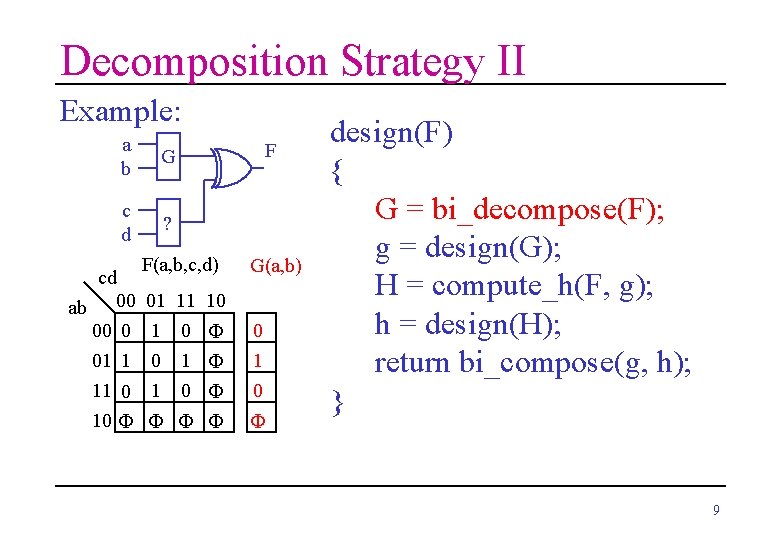
Decomposition Strategy II Example: a b G c d ? cd ab 00 00 0 01 1 11 0 10 F F F(a, b, c, d) G(a, b) 01 1 0 1 0 1 0 10 F F F F design(F) { G = bi_decompose(F); g = design(G); H = compute_h(F, g); h = design(H); return bi_compose(g, h); } 9

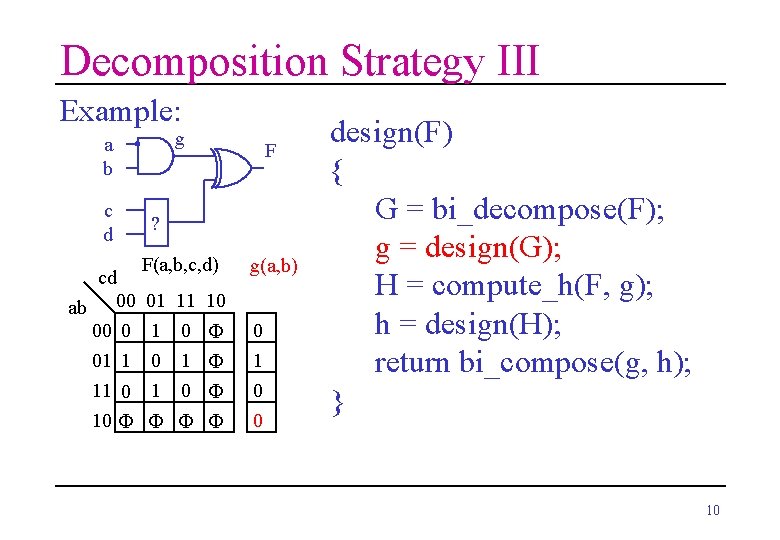
Decomposition Strategy III Example: g a b c d cd ab 00 00 0 01 1 11 0 10 F F ? F(a, b, c, d) 01 1 0 1 11 0 g(a, b) 10 F F F 0 1 0 0 design(F) { G = bi_decompose(F); g = design(G); H = compute_h(F, g); h = design(H); return bi_compose(g, h); } 10

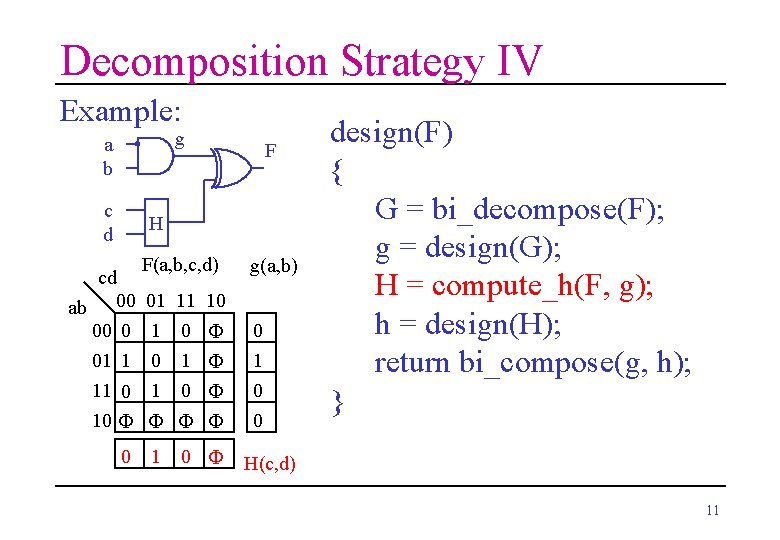
Decomposition Strategy IV Example: g a b c d F H cd ab 00 00 0 01 1 11 0 10 F 0 F(a, b, c, d) 01 1 0 1 11 0 1 0 F g(a, b) 10 F F F 0 1 0 0 design(F) { G = bi_decompose(F); g = design(G); H = compute_h(F, g); h = design(H); return bi_compose(g, h); } H(c, d) 11

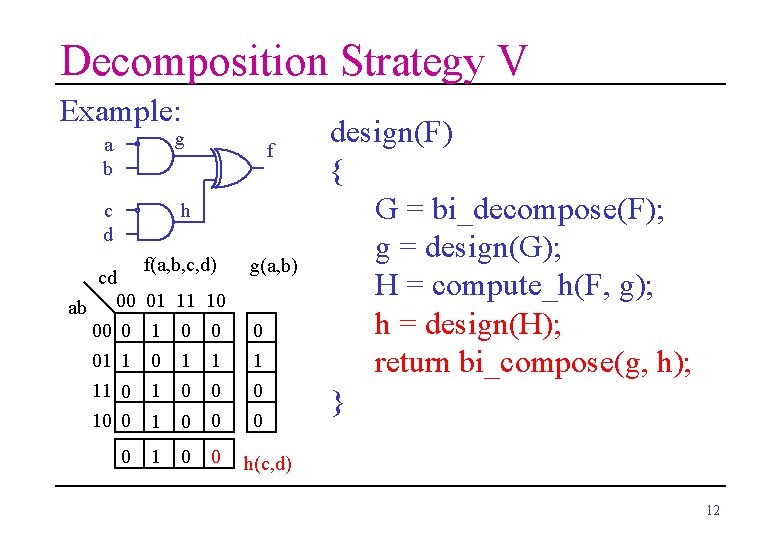
Decomposition Strategy V Example: a b g c d h cd ab 00 00 0 01 1 11 0 10 0 0 f f(a, b, c, d) 01 1 0 1 11 0 1 10 0 1 0 0 g(a, b) 0 1 0 0 design(F) { G = bi_decompose(F); g = design(G); H = compute_h(F, g); h = design(H); return bi_compose(g, h); } h(c, d) 12

Function Sets in Bi-Decomposition • Pass as many decomposition functions to the next stage of decomposition as possible. • For OR and AND decomposition ISFs are sufficient to describe all decomposed functions. • In EXOR decomposition ISFs describe only a small fraction of all possible subfunctions G(A, C) and H(B, C). 13

EXOR-Decomposition of Functions • A function f(A, B, C) is EXOR-decomposable if its decomposition chart consists of two types of columns one being the negation of the other. • There are two decomposition functions g(A, C), the first column and its negation. • Example: cd f(a, b, c, d) g 1(a, b) g 2(a, b) ab 00 00 0 01 1 11 0 10 0 01 1 0 1 1 11 0 10 0 1 0 1 1 14

EXOR-Decomposition of ISFs I • An ISF F(A, B, C) can consists of independent parts. • Each independent part consists of horizontally or vertically connected cares in the decomposition chart. cd F(a, b, c, d) ab 00 01 11 10 00 0 1 F F 01 1 0 F F 11 F F 0 0 10 F F 0 0 15

EXOR-Decomposition of ISFs II • Each independent part has an ISF Gi(A, C) and its negation as decomposition functions. • All decomposition functions gi are combinations of the Gi or their negation (/Gi). • Function set is not an ISF new data structure cd F(a, b, c, d) G 1(a, b) G 2(a, b) ab 00 01 11 10 00 0 1 F F 01 1 0 F F 11 F F 0 0 0 F 10 F F 0 0 0 F G 1ÇG 2 0 1 0 0 0 0 1 1 16

Combinational ISFs (C-ISF) • A C-ISF is a set of functions specified by a set of component ISFs with disjoint care sets. • The cares of each component ISF may be negated. • A C-ISF contains 2#component ISF functions. F 1(a, b) F 2(a, b) ab 00 01 11 10 0 1 F F 0 0 F<F 1, F 2> f 1 ={f 1, f 2, f 3, f 4} f 2 f 3 f 4 0 1 0 0 0 0 1 1 17

Decomposition of C-ISFs I • Each component ISF Fi of a C-ISF F<F 1, ¼, Fn> can be negated. • The decomposability of the function depends on the pattern of negations of its component ISFs. • A large number of component ISFs is possible. • We propose a greedy algorithm that successively adds the component ISFs to the resulting ISF. 18

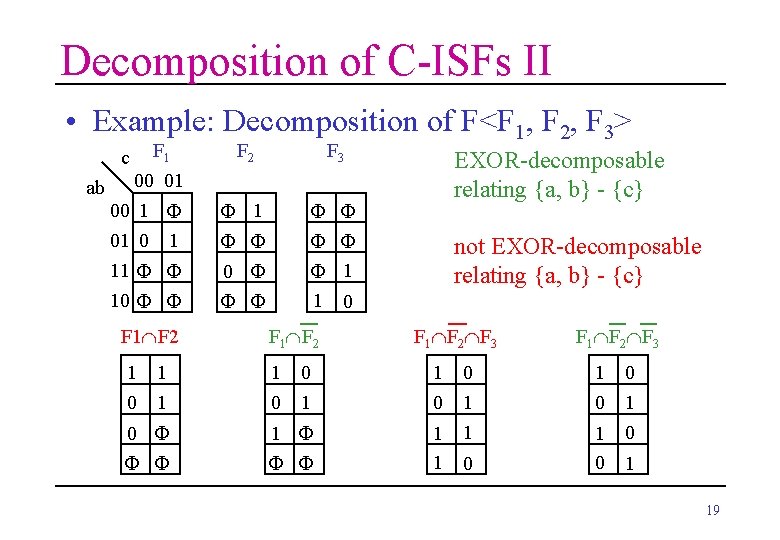
Decomposition of C-ISFs II • Example: Decomposition of F<F 1, F 2, F 3> F 1 ab 00 01 00 1 F 01 0 1 11 F F 10 F F c F 2 F 3 F 1 F F 0 F F F F 1 1 0 EXOR-decomposable relating {a, b} - {c} not EXOR-decomposable relating {a, b} - {c} F 1ÇF 2 1 1 1 0 1 0 1 1 0 0 F F F 1ÇF 2ÇF 3 F 1ÇF 2ÇF 3 1 0 1 19

Multi-Valued Bi-Decomposition • Function sets of Boolean functions can be generalized to function sets of multi-valued functions. • EXOR-decomposition can be extended to MODSUM- (sum modulo n) decomposition. • AND- and OR-decompositions correspond to MIN- and MAX-decompositions 20

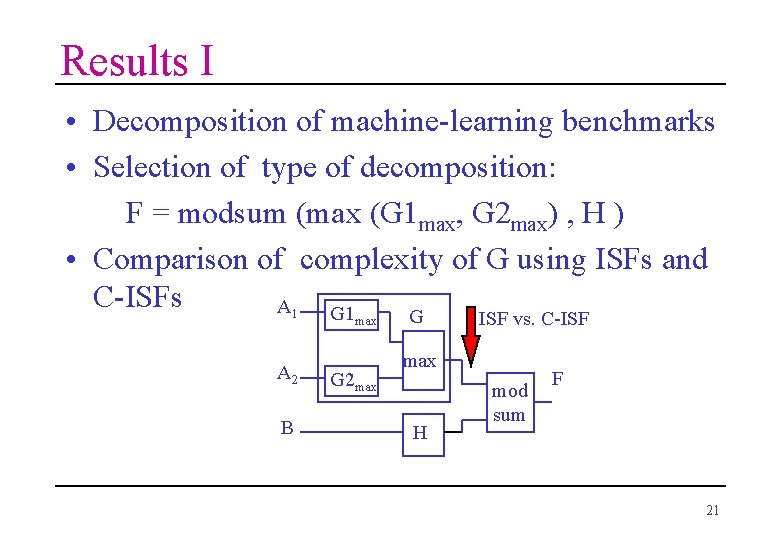
Results I • Decomposition of machine-learning benchmarks • Selection of type of decomposition: F = modsum (max (G 1 max, G 2 max) , H ) • Comparison of complexity of G using ISFs and C-ISFs A 1 G ISF vs. C-ISF max A 2 B G 2 max H mod sum F 21

Results II #inp - Number of Inputs DFC(F)=mo(mi 1*mi 2*. . . *min) DFC: discrete function cardinality 22

Conclusion • Function sets are a generalization of ISFs. • C-ISFs are a particular class of function sets that describe the decomposed functions of EXORdecomposition • C-ISFs can be efficiently bi-decomposed • Better decompositions can be found using C-ISFs instead of ISFs 23

Further Work • Applications – Ashenhurst and Curtis decompositions – finite state machine design (set of functions is used to represent set of state encodings) • Extensions – function sets for multiple output functions – a new concept of sets of relations 24