Biconnected Graph Articulation Points Biconnected Graph A biconnected

Biconnected Graph Articulation Points

Biconnected Graph • A biconnected graph has at least 2 distinct paths (no common edges or vertices) between all vertex pairs • Any graph that is not biconnected has one or more articulation points • Vertices, that, if removed, will separate the graph • Any graph that has no articulation points is biconnected • Thus we can determine that a graph is biconnected if we look for, but do not find any articulation points

Finding articulation points • DFS pre-order traversal • Two arrays

DFS pre-order traversal public Biconnected(Graph G) { pre = new int[G. V()]; for (int v = 0; v < G. V(); v++) pre[v] = -1; for (int v = 0; v < G. V(); v++) if (pre[v] == -1) dfs(G, v); } private void dfs(Graph G, int v) { pre[v] = cnt++; for (int w : G. adj(v)) { if (pre[w] == -1) { dfs(G, w); } } }

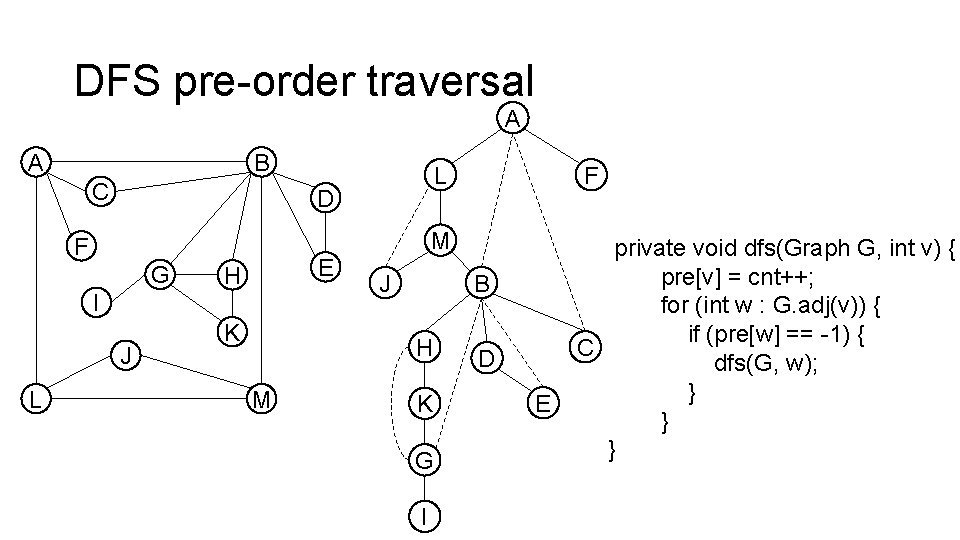
DFS pre-order traversal A A B C D F G E H I J L K M J B H M F L K G I D E private void dfs(Graph G, int v) { pre[v] = cnt++; for (int w : G. adj(v)) { if (pre[w] == -1) { C dfs(G, w); } } }

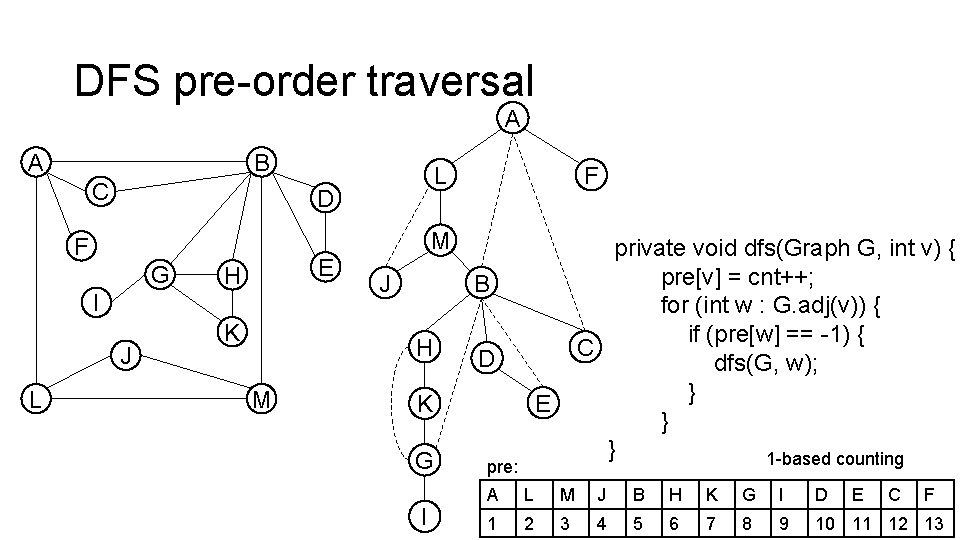
DFS pre-order traversal A A B C D F G E H I J L K M J private void dfs(Graph G, int v) { pre[v] = cnt++; for (int w : G. adj(v)) { if (pre[w] == -1) { C dfs(G, w); } } } 1 -based counting B H M F L D E K G I pre: A L M J B H K G I D E C F 1 2 3 4 5 6 7 8 9 10 11 12 13

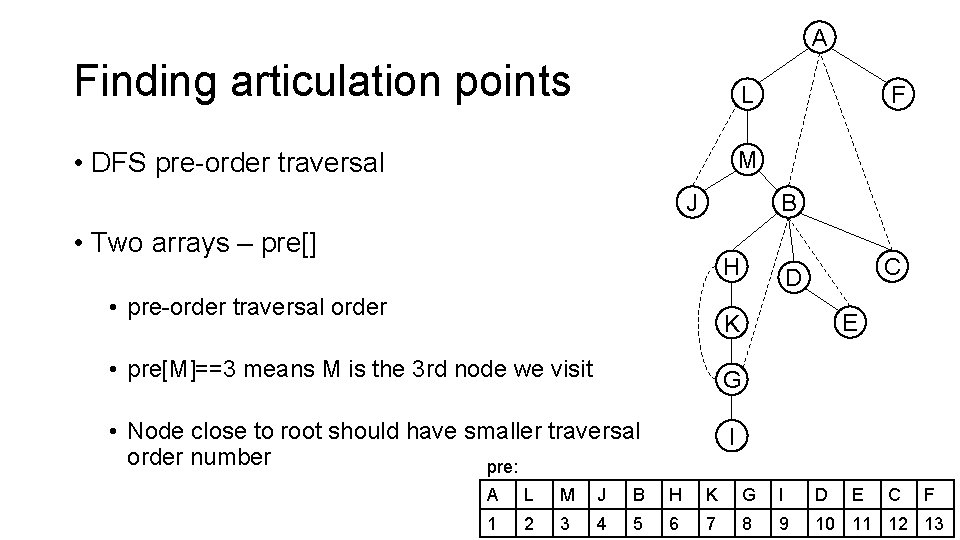
A Finding articulation points L • DFS pre-order traversal M J F B • Two arrays – pre[] H • pre-order traversal order C D E K • pre[M]==3 means M is the 3 rd node we visit G • Node close to root should have smaller traversal order number pre: I A L M J B H K G I D E C F 1 2 3 4 5 6 7 8 9 10 11 12 13

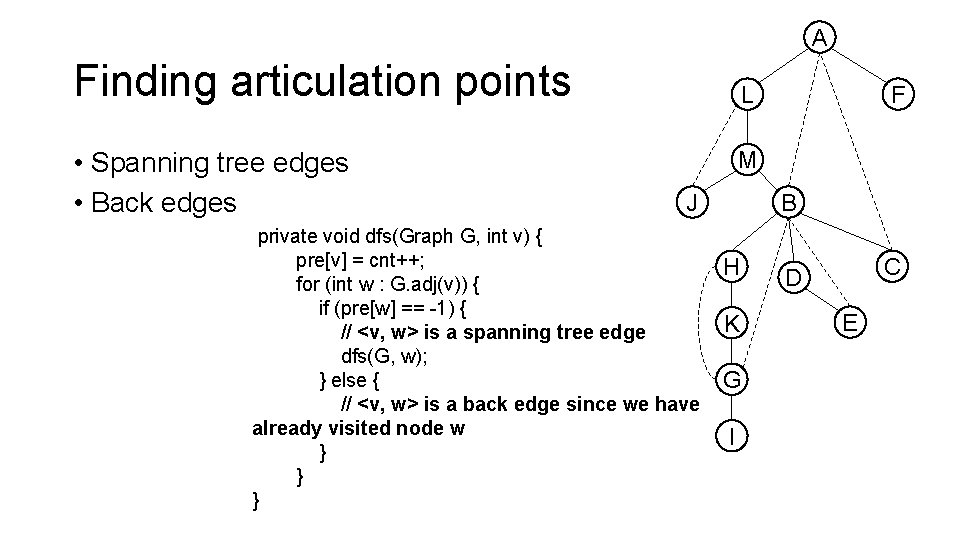
A Finding articulation points • Spanning tree edges • Back edges F L M J private void dfs(Graph G, int v) { pre[v] = cnt++; for (int w : G. adj(v)) { if (pre[w] == -1) { // <v, w> is a spanning tree edge dfs(G, w); } else { // <v, w> is a back edge since we have already visited node w } } } B H K G I C D E

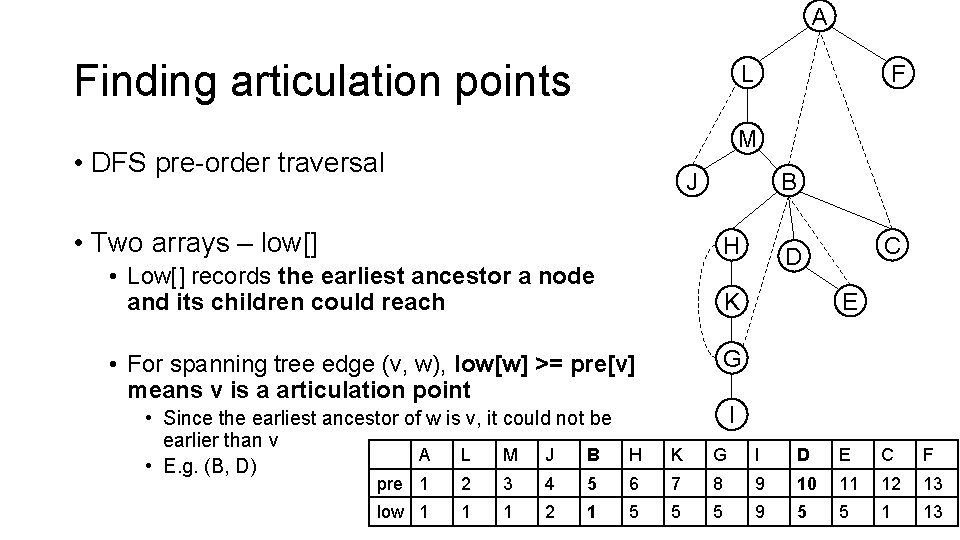
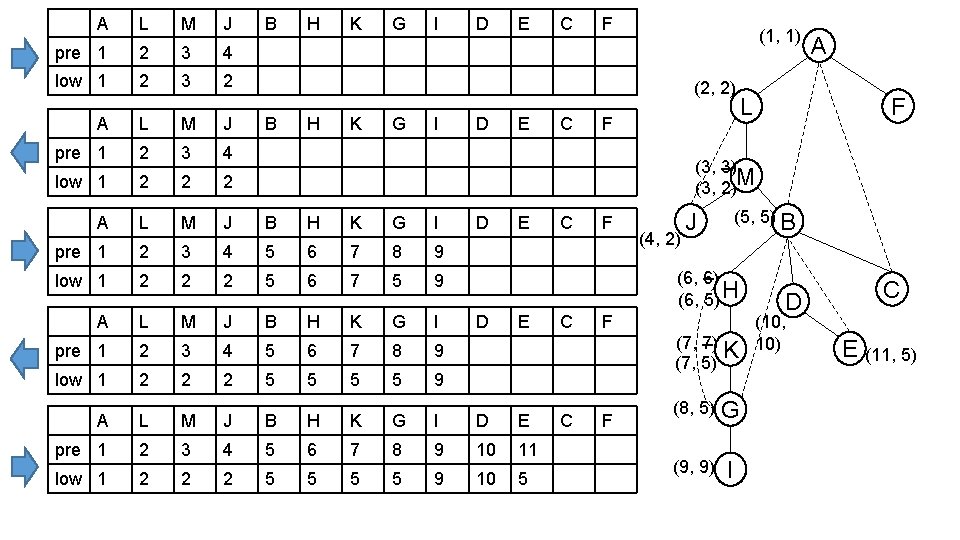
A Finding articulation points F L M • DFS pre-order traversal J B • Two arrays – low[] H • Low[] records the earliest ancestor a node and its children could reach E K G • For spanning tree edge (v, w), low[w] >= pre[v] means v is a articulation point • Since the earliest ancestor of w is v, it could not be earlier than v A L M J B H • E. g. (B, D) C D I K G I D E C F pre 1 2 3 4 5 6 7 8 9 10 11 12 13 low 1 1 1 2 1 5 5 5 9 5 5 1 13

A Finding articulation points • Low[v] records the earliest ancestor node v and its children could reach • Min of three cases M J B H K • 1) Basic case: low[v] = prev[v] G • Node v could reach itself • Def: Low[] records the earliest ancestor a node and its children could reach v F L I C D E

A Finding articulation points M • Low[v] records the earliest ancestor node v and its children could reach J B H • Min of three cases K • 2) v has back edges (v, w): G • Compare pre[w] to low[v] • fix v, for all w • E. g. node G choose B among {K, H, B} w • When we search from node v, we know pre[w] since we already visited the node • w could not be the parent of v A L M J B H K G I D E C F pre 1 2 3 4 5 6 7 8 9 10 11 12 13 low 1 1 1 2 1 5 5 5 9 5 5 1 13 F L v I C D E

A Finding articulation points M • Low[v] records the earliest ancestor node v and its children could reach J B H • Min of three cases K • 3) v has spanning tree edges (v, w): G • Compare low[w] to low[v] I • E. g. node M choose A since its children B could reach A • What if children of B could have smaller low value? • When we search from node v, we DO NOT know low[w] until we return from the next recursive call v A L M J B H K G I D E C F pre 1 2 3 4 5 6 7 8 9 10 11 12 13 low 1 1 1 2 1 5 5 5 9 5 5 1 13 F L w C D E

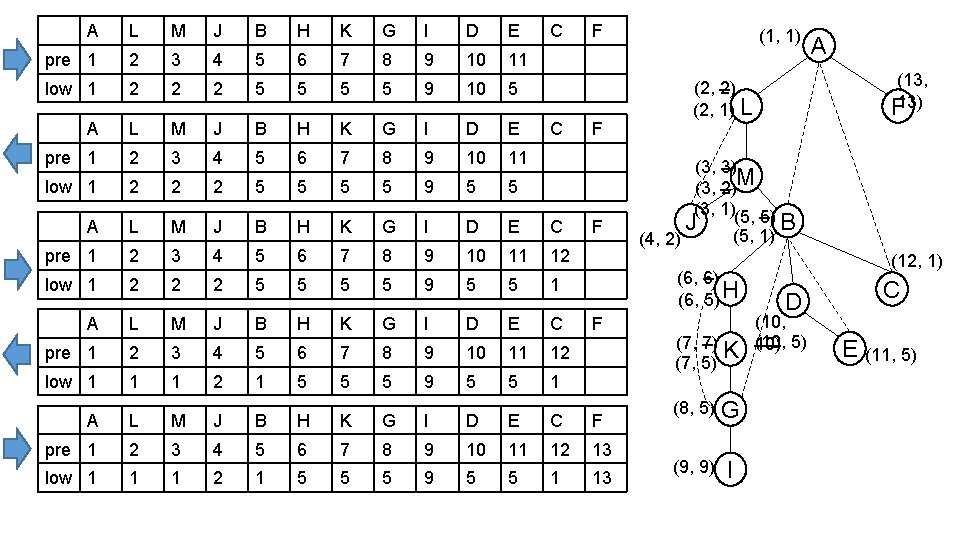
A Finding articulation points • Min of three cases • 1) Basic case: M J B • low[v] = prev[v] H • compare pre[w] to low[v], e. g. node G K • compare low[w] to low[v], e. g. node M G • 2) v has back edges (v, w): • 3) v has spanning tree edges (v, w): F L C D E I • For the case 3), we have to make the comparison after recursive call, since then we have information of low[w] • Decide the low[] value of leaf node at the beginning • Update low[] in the path • E. g. Only when we know low[C]=1, we could finally decide that low[B]=1, then low[M]=1, low[L]=1

private void dfs(Graph G, int u, int v) { int children = 0; pre[v] = cnt++; Case 1: basic low[v] = pre[v]; public Biconnected(Graph G) { low = new int[G. V()]; pre = new int[G. V()]; articulation = new boolean[G. V()]; for (int v = 0; v < G. V(); v++) Case 3: low[v] = -1; spanning tree for (int v = 0; v < G. V(); v++) edge pre[v] = -1; for (int v = 0; v < G. V(); v++) if (pre[v] == -1) dfs(G, v, v); } for (int w : G. adj(v)) { if (pre[w] == -1) { children++; dfs(G, v, w); low[v] = Math. min(low[v], low[w]); if (low[w] >= pre[v] && u != v) articulation[v] = true; } else if (w != u) Case 2: back edge Special case for root node low[v] = Math. min(low[v], pre[w]); } if (u == v && children > 1) articulation[v] = true; } The condition

A L M J pre 1 2 3 4 low 1 2 3 2 B H K G I D E C F (1, 1) (2, 2) A L M J B H K G I D E pre 1 2 3 4 low 1 2 2 2 A L M J B H K G I pre 1 2 3 4 5 6 7 8 9 low 1 2 2 2 5 6 7 5 9 A L M J B H K G I pre 1 2 3 4 5 6 7 8 9 low 1 2 2 2 5 5 9 A L M J B H K G I D E pre 1 2 3 4 5 6 7 8 9 10 11 low 1 2 2 2 5 5 9 10 5 C F A F L (3, 3) M (3, 2) D E C F (4, 2) J (5, 5) B (6, 6) (6, 5) H D E C F (7, 7) K (7, 5) C F (8, 5) G (9, 9) I C D (10, 10) E (11, 5)

A L M J B H K G I D E C pre 1 2 3 4 5 6 7 8 9 10 11 low 1 2 2 2 5 5 9 10 5 A L M J B H K G I D E pre 1 2 3 4 5 6 7 8 9 10 11 low 1 2 2 2 5 5 9 5 5 A L M J B H K G I D E C pre 1 2 3 4 5 6 7 8 9 10 11 12 low 1 2 2 2 5 5 9 5 5 1 A L M J B H K G I D E C pre 1 2 3 4 5 6 7 8 9 10 11 12 low 1 1 1 2 1 5 5 5 9 5 5 1 A L M J B H K G I D E C F pre 1 2 3 4 5 6 7 8 9 10 11 12 13 low 1 1 1 2 1 5 5 5 9 5 5 1 13 C F F F (1, 1) (13, F 13) (2, 2) (2, 1) L (3, 3) M (3, 2) (3, 1)(5, 5) J B (5, 1) (4, 2) (6, 6) (6, 5) H F A (7, 7) K (7, 5) (8, 5) G (9, 9) I (12, 1) C D (10, 5) 10) E (11, 5)