BIBS SEOUL NATIONAL UNIVERSITY Bioinformatics Biostatistics Lab Categorical

BIBS SEOUL NATIONAL UNIVERSITY Bioinformatics & Biostatistics Lab. Categorical Data Analysis & Logistic Regression 수원대학교 통계정보학과 김진흠 ㈜ 마케팅랩 파트너스 선임연구원 이은경

SNU BIBS Outline ü Two-way contingency tables: RR, Odds ratio, Chi-square tests ü Three-way contingency tables: Conditional independence, Homogeneous association, Common odds ratio ü Logistic regression: Dichotomous response ü Logistic regression: Polytomous response BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS First example: Aspirin & heart attacks ü Clinical trials table of aspirin use and MI Ø Test whether regular intake of aspirin reduces mortality from cardiovascular disease Ø Data set Myocardial Infarction Group Yes No Total Placebo 189 10, 845 11, 034 Aspirin 104 10, 933 11, 037 Ø Prospective sampling design: Cohort studies, Clinical trials BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Second example: Smoking & heart attacks ü Case-control study: and MI table of smoking status Ø Compare ever-smokers with nonsmokers in terms of the proportion who suffered MI Ø Data set Ever. Smoker Myocardial Infarction Controls Yes 172 173 No 90 346 262 519 Total Ø Retrospective sampling design: Case-control study, Cross-sectional design ü Remark: Observational studies vs. experimental study BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Comparing proportions in table ü Difference: ü Relative risk: Ø Useful when both proportions Ø 0 or 1 : RR is more informative Ø : Response is independent of group BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example (revisited) ü 1 st example Ø =0. 0171－0. 0094=0. 0077, 95% CI=(0. 005, 0. 011) ² Taking aspirin diminishes heart attack Ø , 95% CI=(1. 43, 2. 3) ² Risk of MI is at least 43% higher for the placebo group ü 2 nd example Ø , : Not estimable, meaningless even though possible Ø Estimate proportions in the reverse direction ² Proportion of smoking given MI status: (suffering MI), (Not suffered MI) BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Association measure: odds ratio ü Def’n: ü Meaning Ø When two variables are independent, i. e. , Ø When odds of success (in row 1) > (in row 2) Ø When odds of success (in row 1) < (in row 2) ü Remark: When both variables are response, (called cross-product ratio) using joint probabilities BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Properties of odds ratio ü Values of father from 1 in a given direction represent stronger association ü When one value is the inverse of the other, two values of are the same strength of association, but in the opposite directions Ø ü Not changed when the table orientation reverses Ø Unnecessary to identify one classification as a response variable BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example (revisited) ü 1 st example Ø , 95% CI=(1. 44, 2. 33) ² Estimated odds is 83% higher for the placebo group ² ü 2 nd example Ø Ø Rough estimate of RR=3. 8 ² Women who had ever smoked were about four times as likely to suffer as women who had never smoked BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Independence tests ü Hypothesis: ü Two chi-square tests Ø Under , estimated expected frequency Ø Pearson’s = Ø Likelihood ratio(LR) statistic Ø For a large sample, follow a chi-squared null distribution with ü Remark: When the chi-squared approximation is good. If not, apply Fisher’s exact test BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example: AZT use & AIDS ü Development of AIDS symptoms in AZT use and race Ø Study on the effects of AZT in slowing the development of AIDS symptoms Ø Data set Symptoms Race AZT Use Yes No Total White Yes 14 93 107 No 32 81 113 Yes 11 52 63 No 12 43 55 Black BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Three interests in table ü Conditional independence? When controlling for race, AZT treatment and development of AIDS symptom are independent Ø Use Cochran-Mantel-Haenszel(CMH) test Ø Summarize the information from partial tables ü Homogeneous association? Odds ratios of AZT treatment and development of AIDS symptom are common for each race Ø Use Breslow-Day test ü Common odds ratio? Use Mantel-Haenszel estimate BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example (AZT use & AIDS revisited) ü CMH=6. 8( =1) with -value=0. 0091 Ø Not independent! ü Breslow-Day=1. 39( =1) with -value=0. 2384 Ø Homogeneous association! ü Common odds ratio=0. 49 Ø For each race, estimated odds of developing symptoms are half as high for those who took AZT BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Overview of types of generalized linear models(GLMs) ü Three components: Random component (response variable), Linear predictor (linear combination of covariates), Link function ü Types of GLMs Random Component Link Systematic Component Model Normal Identity Continuous Regression Normal Binomial Poisson Multinomial Identity Logit Log Generalized logit Categorical Mixed Analysis of variance Analysis of covariance Logistic regression Loglinear Multinomial response BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Logistic regression with a quantitative covariate ü Model: ü Another representations Ø Odds= ² Odds at level equals the odds at multiplied by Ø ² Curve ascends ( ) or descends ( ) ² The rate of change increases as increases BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example: Horseshoe crabs ü Binary response Ø if a female crab has at least one satellite; otherwise ü Covariate: female crab’s width ü Data set Width < 23. 25－24. 25－25. 25－26. 25－27. 25－28. 25－29. 25 > 29. 25 Number Cases 14 14 28 39 22 24 18 14 Number Having Satellites 5 4 17 21 15 20 15 14 BIOSTATISTICS FOR BIOINFORMATICS

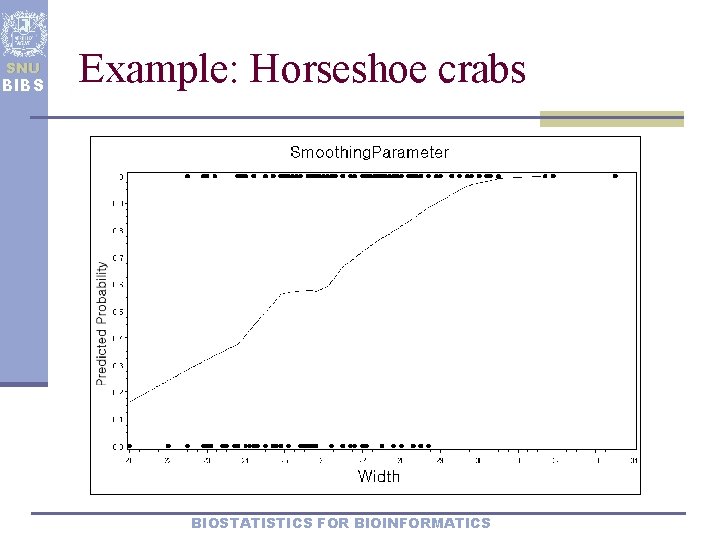
SNU BIBS Example: Horseshoe crabs BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Goodness-of-fit tests ü Working model: parameters in : ü Hypothesis: number of settings: number of fits the data ü Pearson’s statistic: ü Deviance statistic: ü approximately follow a chi-square null distribution with BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Inference for parameters ü Interval estimation: ü Two significance tests: Ø Wald test: Use Ø Likelihood ratio test: Use , log-likelihood function Ø Two tests have a large-sample chi-squared null distribution with BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example (Horseshoe crabs revisited) ü Fitted model: ü : larger at lager width ( ) ü There is a 64% increase in estimated odds of a satellite for each centimeter increase in width ( ) ü with -value=0. 506; with -value=0. 4012 ü 95% CI for =(0. 298, 0. 697) ü Significance test: Wald=23. 9 ( =1) with -value < 0. 0001; LRT=31. 3 ( =1) with -value < 0. 0001 BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Logistic regression with qualitative predictors: AIDS symptoms data ü ü Use indicator variables for representing categories of predictors ü Logits implied by indicator variables Logit 0 0 1 1 1 BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Logistic regression with qualitative predictors: AIDS symptoms data ü =difference between two logits (i. e. , log of odds ratio) at a fixed category of ü ü Homogeneous association model BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Equivalence of contingency table & logistic regression ü Conditional independence: CMH test vs. ü Homogeneous association: Breslow-Day test vs. Goodness-of-fit test ü Common odds ratio estimate: Mantel-Haenszel estimate vs. BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Computer Output for Model with AIDS Symptoms Data Log Likelihood －167. 5756 Analysis of Maximum. Likelihood Estmates Parameter Intercept azt race Estimate －1. 0736 －0. 7195 0. 0555 Std Error 0. 2629 0. 2790 0. 2886 Wald Chi-Square 16. 6705 6. 6507 0. 0370 Pr > Chi. Sq <. 0. 001 0. 0099 0. 8476 Chi-Square 6. 87 0. 04 Pr>Chi. Sq 0. 0088 0. 8473 LR Statistics Source azt race Obs 1 2 3 4 Df 1 1 race azt y n pi_hat lower upper 1 1 0 0 1 0 14 32 11 12 107 113 63 55 0. 14962 0. 26540 0. 14270 0. 25472 0. 09897 0. 19668 0. 08704 0. 16953 0. 21987 0. 34774 0. 22519 0. 36396 BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Logistic regression with mixed predictors: Horseshoe crabs data ü ü For color=medium light, For color=medium dark, ü For controlling BIOSTATISTICS FOR BIOINFORMATICS

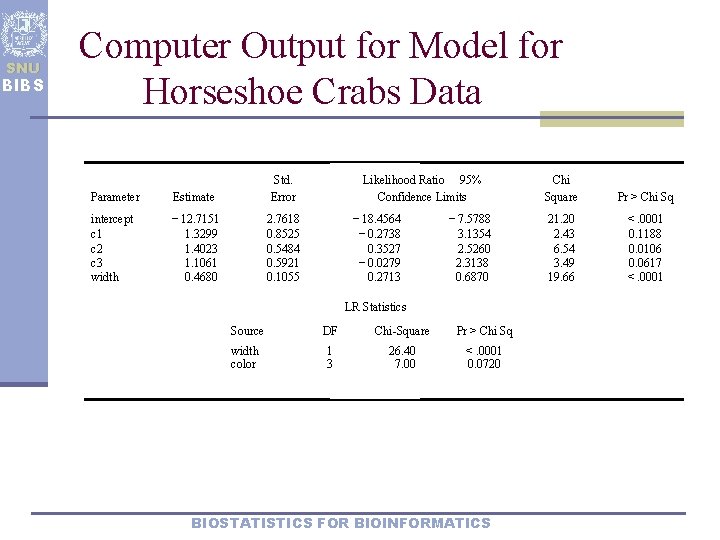
SNU BIBS Computer Output for Model for Horseshoe Crabs Data Parameter Estimate Std. Error intercept c 1 c 2 c 3 width －12. 7151 1. 3299 1. 4023 1. 1061 0. 4680 2. 7618 0. 8525 0. 5484 0. 5921 0. 1055 Likelihood Ratio 95% Confidence Limits －18. 4564 －0. 2738 0. 3527 －0. 0279 0. 2713 －7. 5788 3. 1354 2. 5260 2. 3138 0. 6870 LR Statistics Source DF Chi-Square Pr > Chi Sq width color 1 3 26. 40 7. 00 <. 0001 0. 0720 BIOSTATISTICS FOR BIOINFORMATICS Chi Square Pr > Chi Sq 21. 20 2. 43 6. 54 3. 49 19. 66 <. 0001 0. 1188 0. 0106 0. 0617 <. 0001

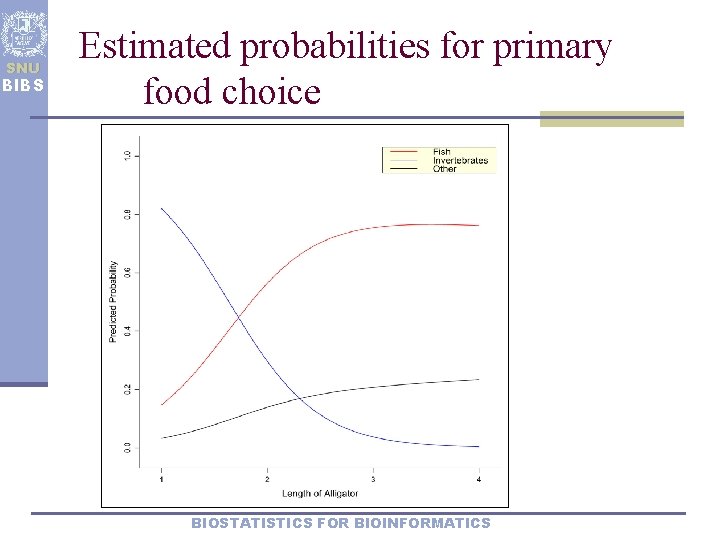
SNU BIBS Estimated probabilities for primary food choice BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Logistic regression: ploytomous ü Model categorical responses with more than two categories ü Two ways Ø Use generalized logits function for nominal response Ø Use cumulative logits function for ordinal response ü Notation Ø Ø number of categories response probabilities with BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Generalized logit model: nominal response ü Baseline-category logit: Pair each category with a baseline category Ø when is the baseline ü Model with a predictor Ø Ø The effects vary according to the category paired with the baseline Ø These pairs of categories determine equations for all other pairs of categories ² Eg, for a pair of categories ü Remark: Parameter estimates are same no matter which category is the baseline BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example: Alligator food choice ü 59 alligators sample in Lake Gorge, Florida ü Response: Primary food type found in alligator’s stomach Ø Fish(1), Invertebrate(2), Other(3, baseline category) ü Predictor: alligator length, which varies 1. 24~3. 89(m) ü ML prediction equations Ø Ø ² Larger alligator seem to select fish than invertebrates ü Independence test: Food choice & length Ø LRT=16. 8006( ) with BIOSTATISTICS FOR BIOINFORMATICS -value=0. 0002

SNU BIBS Cumulative logit model: ordinal response ü Logit of a cumulative probability Ø Ø Categories 1 to : combined, Categories to : combined ü Cumulative proportional odds model with a predictor Ø Ø The effect of are identical for all cumulative logits Ø Any one curve for is identical to any of others shifted to the right or shifted to the left Ø For =log of odds ratio is ² Proportional to the difference between ² Same for each cumulative probability values BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example: Political ideology & party affiliation ü Response: Political ideology with five-point ordinal scale ü Predictors: Political party(Democratic, Republican) Political Ideology Political Party Very Slightly Liberal Moderate Slightly Conservative Very Conservative Democratic 80 81 171 41 55 Republican 30 46 148 84 99 BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Example: Political ideology & party affiliation ü Parameter inference Ø , ² Democrats tend to be more liberal than Republicans Ø Wald=57. 1( ) with -value < 0. 0001 ² Strong evidence of an association Ø 95% CI for =(0. 72, 1. 23) or =(2. 1, 3. 4) ² At least twice as high for Democrats as for Republicans ü Goodness-of-fit Ø with -value=0. 2957 BIOSTATISTICS FOR BIOINFORMATICS Good adequacy!

SNU BIBS Another logit forms for ordinal response categories ü Adjacent-categories logit Ø Ø Adjacent-categories logits determine the logits for all pairs of response categories ü Continuation-ratio logit Ø Form 1: ² Contrast each category with a grouping of categories from lower levels of response scale Ø Form 2: ² Contrast each category with a grouping of categories from higher levels of response scale BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS Summary ü Two-way contingency tables: RR, Odds ratio, Chi-square tests ü Three-way contingency tables: Conditional independence, Homogeneous association, Common odds ratio ü Logistic regression: Dichotomous response ü Logistic regression: Polytomous response BIOSTATISTICS FOR BIOINFORMATICS

SNU BIBS References ü Agresti, A. (1996). An Introduction to Categorical Data Analysis, Wiley: New York (Also the 2 n d edition is available) ü Stokes, M. E. , Davis, C. S. , and Koch, G. G. (2000). Categorical Data Analysis Using The SAS System, Second Ed. , SAS Inc. : Cary BIOSTATISTICS FOR BIOINFORMATICS