Biases and Paradoxes of human decision making Overview

Biases and Paradoxes of human decision making Overview: q q Empirical results concerning decision biases Paradoxes Mental accounting Prospect theory

Biases and Paradoxes of human decision making Biases (empirical results): q q q q q Framing effects. Sunk cost effect. Independence from irrelevant alternatives. Relativity Bias. Endowment effect. Intransitive preferences. Preference reversals. Less is more effect. Decision diversification / Probability matching.

Biases and Paradoxes of human decision making Framing Effects: Excerpt from the Marburger magazine Express: Up to the seventies, 20 percent of the children with a heart disease died during the first days of their lives. One can find such a child on the cemetery for nearly every bigger family: babies who came blue into the world, struggling for breath for a few days and then dying in the arm of their mothers. ‘Today eighty percent survive’ Bauer explains with a certain element of pride. [Translated by M. S. ] [Bis in die siebziger Jahre starben 20 Prozent der herzkranken Kinder in den ersten Lebenstagen. Fast jede grössere Familie hat so ein Kind auf dem Friedhof: Babys, die blau auf die Welt kamen, ein paar Tage nach Luft rangen und dann im Arm der Mutter starben. ‚Heute überleben achtzig Prozent‘ sagt Bauer mit leichtem Stolz. ]

Biases and Paradoxes of human decision making Framing effects: Tversky & Kahneman (1981): Asian disease problem Group 1 (N = 152): Imagine that the U. S. is preparing for the outbreak of an un usual Asian disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimate of the consequences of the programs are as follows: If Program A is adopted, 200 people will be saved. If Program B is adopted, there is 1/3 probability that 600 people will be saved and 2/3 probability that no people will be saved. 72% preferred Program A.

Biases and Paradoxes of human decision making Framing effects: Tversky & Kahneman (1981): Asian disease problem Group 2 (N = 155): Imagine that the U. S. is preparing for the outbreak of an un usual Asian disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Assume that the exact scientific estimate of the consequences of the programs are as follows: If Program C is adopted, 400 people will die. If Program D is adopted, there is 1/3 probability that nobody will die, and 2/3 probability that 600 people will die. 78% preferred Program D.

Biases and Paradoxes of human decision making Framing effects : Tversky & Kahneman (1981): Asian disease problem The two problems differ only with respect to whether the options were framed in terms of wins (first problem): If Program A is adopted, 200 people will be saved. If Program B is adopted, there is 1/3 probability that 600 people will be saved and 2/3 probability that no people will be saved. Or losses (second problem): If Program C is adopted, 400 people will die. If Program D is adopted, there is 1/3 probability that nobody will die, and 2/3 probability that 600 people will die. In case of sure wins people are risk aversive whereas in case of sure losses they are risk seeking.

Biases and Paradoxes of human decision making Framing effects (Medical Decisions): Mc. Neil, Pauker, Sox, & Tversky, 1982 3 groups: a. Radiologists (N = 424) b. Graduate students who had completed coursework in statistics and decision theory (N = 491). c. Ambulatory patients with different problems (N = 238). All participants received summary information on two forms of treatment for lung cancer: surgery vs. radiation therapy. In approximately half of the cases, the summary information was framed in terms of probability of survival after a parti cular amount of time (e. g. 68% chance of living for more than one year).

Biases and Paradoxes of human decision making Framing effects (Medical Decisions): Mc. Neil, Pauker, Sox, & Tversky, 1982 In approximately half of the cases, the summary information was framed in terms of probability of survival after a parti cular amount of time (e. g. 68% chance of living for more than one year). In the other cases the summary information was cast in terms of mortality (e. g. a 32 percent chance of dying by the end of one year). Ø Surgery was preferred 75 percent of the time in the sur vival frame but only 58 percent in the mortality frame. Ø No difference between groups.

Biases and Paradoxes of human decision making Sunk cost effect: Concept: The Sunk Cost Effect consists in a tendency to continue an endeavor once an investment in money, effort, or time has been made. This tendency is based on the desire not to appear wasteful. In case of the prior investment influencing the current decision despite the fact that it objectively should not influence it one can talk of a fallacy.

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 1 Assume that you have spent $100 on a ticket for a weekend ski trip to Michigan. Several weeks later you buy a $50 ticket for a weekend ski trip to Wisconsin. You think you will enjoy the Wisconsin ski trip more than the Michigan ski trip. As you are putting your just-purchased Wisconsin ski trip ticket in your wallet, you notice that the Michigan ski trip and the Wisconsin ski trip are for the same weekend! It’s too late to sell either ticket, and you cannot return either one. You must use one ticket and not the other. Which ski trip will you go on? A. $100 ski trip to Michigan (N = 33) B. $50 ski trip to Wisconsin (N = 28) Thus, about 53% chose the less attractive Michigan trip. The prior investment seems to have influenced this decision.

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 2 (Field study) Visitors of the Ohio University Theater who wanted to purchase a season ticket were offered a ticket. Season tickets were of three price classes: $15, $7, and $2. Each visitor was randomly assigned to a specific price cate gory. She did not know that there were different categories. Result: People with $15 tickets visited more plays in the first half of the season than those of the other two price categories.

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 3 Scenario A. As the president of an airline company, you have invested 10 million dollars of the company’s money into a research project. The purpose was to build a plane that would not be detected by conventional radar, in other words, a radar blank plane. When the project is 90% completed, another firm begins marketing a plane that cannot be detected by radar. Also, it is apparent that their plane is much faster and far more economical than the plane your company is building. The question is: should you invest the last 10% of the research funds to finish your radar blank plane? Yes: N = 41 No: N = 7

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 3, continued Scenario B. As president of an airline company, you have received a suggestion from one of your employees. The suggestion is to use the last 1 million dollars of your research funds to develop a plane that would not be detected by conventional radar, in other words, a radar blank plane. However, another firm has just begun marketing a plane that cannot be detected by radar. Also, it is apparent that their plane is much faster and far more economical than the plane your company could build. The question is: should you invest the last million dollars of your research funds to build the radar blank plane proposed by your employee? Yes: N = 10 No: N = 50

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 4 Same scenarios as in Experiment 3. People either got Scena rio A or B and they had to judge the likelihood of a success for the respective scenario: A. 41% success rate B. 34% success rate. Thus, The sunk cost effect influences ratings of success.

Biases and Paradoxes of human decision making Sunk cost effect: Cognitive Mechanism: Sunk cost effect and regret The best explanation of the sunk cost effects is based on regret: The admission that one has wasted resources and the experience of the resulting sure loss produces regret. To avoid these negative feelings, people are willing to spend more resources and to » throw good money after the bad «.

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 6 On your way home you buy a tv dinner on sale for $3 at the local grocery store. A few hours later you decide it is time for dinner, so you get ready to put the tv dinner in the oven. Then you get an idea. You call up your friend to ask if he would like to come over for a quick tv dinner and then watch a good movie on tv. Your friend says “Sure. ” So you go out to buy a second tv dinner. However, all the on sale tv dinners are gone. You therefore have to spend $5 (the regular price) for the tv dinner identical to the one you just bought for $3. You go home and put both dinners in the oven. When the two dinners are fully cooked, you get a phone call. Your friend is ill and cannot come. You are not hungry enough to eat both dinners. You cannot freeze one. You must eat one and discard the other. Which one do you eat?

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985), Experiment 6 (continued) $3: $5: No preference: N=2 N = 21 N = 66 Comments: q Since both dinners are identical there is no reason to prefer one dinner over the other one. q With respect to regret things are different since to waste $3 produces less regret than wasting $5.

Biases and Paradoxes of human decision making Sunk cost effect: Arkes & Blumer (1985) performed further experi ments that demonstrate: q The sunk cost effect can influence future investments. q Personal involvement increases the effect. q The sunk cost effect is present even if no actual loss is involved (Scenario of Experiment 1 with the difference that tickets were not bought but had been won in lottery). q Sophistication in economics does not reduce the sunk cost effect.

Biases and Paradoxes of human decision making Sunk cost effect: The sunk cost effect may also be used in political arguments, for example to help lancing big projects with high investments. q Should I continue an unhappy relationship in which I have q q already invested so much? Should I continue this unhappy job (University study)? I have already spent so much time and effort. Should I leave the movie which is not enjoyable at all? But I have spent Sfr. 15. as entrance fee. Should I make the trip for which I have already paid despite the fact that I feel sick? Ending the Vietnam War: It was argued that this would be a waste of lives.

Biases and Paradoxes of human decision making Sunk cost effect: The sunk cost effect may be influential for different types of decisions (not only financial ones): Example: Construction of a nuclear power plant: In the seventies of the twenties century the Austrian government decided to build an atomic power plant. Since there existed a considerable resistance against this project in the population and the election period was approaching, the government decided to allow for public vote. However, they decided that the vote should take place only after the construction work of the power plant had been finished.

Biases and Paradoxes of human decision making Sunk cost effect: Example: Construction of a nuclear power plant: From an economic perspective, the decision to enable the vote only after having finished the construction is difficult to justify since in case of a rejection additional millions will be wasted. Taking the sunk cost effect into consideration, the decision to delay the vote after the end of erection makes sense due to the increased waste of resources and the resulting regret. This might increase the chances that people would vote in favor of the project. Comment: The policy did not work however, and the project was rejected.

Biases and Paradoxes of human decision making Independence from irrelevant alternatives: It seems intuitively plausible that adding an unattractive alternative to an existing set of alternatives should have no great influence on the relative choice probabilities with respect to the other (more attractive) options. However, peoples’ choice behavior exhibits this sort of influence. Example: Attraction effect (Simenson & Tversky, 1992) One group of subjects had the choice between receiving $6 or a nice Cross pen. This resulted in the following percentages of choices: $6: 64% chose this option. Cross pen: 36% chose this option.

Biases and Paradoxes of human decision making Independence from irrelevant alternatives: Example: Attraction effect (Simenson & Tversky, 1992) A second group received also the two options and, in addi tion, a third one consisting of a less nice Cross pen. $6: 58% chose this option. Cross pen: 46% chose this option. Less attractive Cross pen: 2% chose this option. Obviously, the addition of a less attractive pen increased the attractiveness of the other pen (instead of decreasing it). Note that the less attractive pen was practically never chosen.

Biases and Paradoxes of human decision making Independence from irrelevant alternatives: Example: Compromise effect (Simenson & Tversky, 1992) Given: 3 possible options. A: A camera of high quality and price. B: A camera of intermediate quality and price. C: A camera of low quality and price. If the choice set consisted of Options A and B people chose both options about equally often. Adding Option C the set resulted in higher choice rates for Option B compared to Op tion A. Thus, despite being quite unattractive, C influences the choice probabilities for the other options.

Biases and Paradoxes of human decision making Relative vs. Absolute Savings: People make the value of a specific amount of money to depend on context. Specifically, they take into account the overall money spent. Relative versus absolute savings (Thaler, 1980): Participants received one of the following two versions of a decision problem. Version 1: Imagine that you go to purchase a calculator for $30. The calculator salesperson informs you that the calculator you wish to buy is on sale for $20 at the other branch of the store which is ten minutes away by car. Would you drive to the other store? Option A: Yes, Option B: No.

Biases and Paradoxes of human decision making Relative vs. Absolute Savings: People make the value of a specific amount of money to depend on context. Specifically, they take into account the overall money spent. Relative versus absolute savings (Thaler, 1980): Version 2: Imagine that you go to purchase a jacket for $250. The jacket salesperson informs you that the jacket you wish to buy is on sale for $240 at the other branch of the store which is ten minutes away by car. Would you drive to the other store? Option A: Yes, Option B: No. Result: Significantly more participants were willing to drive to the other store in Version 1 than in Version 2.

Biases and Paradoxes of human decision making Relative vs. Absolute Savings: Cognitive mechanism: Relative versus absolute savings: The results can be explained by means of prospect theory’s utility curves for losses: Initial losses with respect to the status quo are experienced as more painful than additional losses if a certain amount of loss had already occurred. Thus to loose Sfr. 1, 000 is experienced as more unpleasant compared to a loss of additional Sfr. 1, 000 if Sfr. 10, 000 had already been lost. Thus there exists a diminishing negative utility of losses. Peoples’ tendency to focus on relative savings is capitalized by sales persons in case of greater investments. For example, car sellers tend to offer additional facilities that are relatively cheap compared to the ba sic price of the car.

Biases and Paradoxes of human decision making Endowment Effect: Concept: Endowment effect The Endowment Effect consists in peoples’ tendency to value an object higher if they own it. As a result, people's maximum willingness to pay (WTP) to acquire an object is usually lower than the least amount they are willing to accept (WTA). Example: Endowment effect (Kahneman & al. , 1990) Participants were divided into three groups: sellers, buyers, and choosers: Sellers: Participants received a coffee mug and indicated on a list ranging from $0. 00 to $9. 25 in steps of $0. 25 for which price they would sell the mug.

Biases and Paradoxes of human decision making Endowment Effect: Participants were divided into three groups: sellers, buyers, and choosers: Sellers: Participants received a coffee mug and indicated on a list ranging from $0. 00 to $9. 25 in steps of $0. 25 for which price they would sell the mug. Buyers: They used the same list and indicated for which price they would buy the mug. Choosers: They should choose for each price category on the list bet ween the mug and the cash. Result: Median valuations were $7. 12 for sellers, $3. 12 for cho osers and $2. 87 for buyers (choosers & buyers are close together).

Biases and Paradoxes of human decision making Endowment Effect: Cognitive mechanism: Endowment effect According to prospect theory options are evaluated with respect to the current status quo that serves as a point of reference. The withdrawal of an object in one’s own possession is experienced as a loss. The value function is steeper for losses than for gains. By consequence, the money received as a compensation results in a lower relative increase of gain compared to the experienced loss.

Biases and Paradoxes of human decision making Intransitivity of Preferences: q In Chapter 1 it has been shown that people with intransi tive preferences can be made to » money bumps «: One can arrange a sequence of decisions that results in a permanent loss of money for these people. q Intransitive choices can easily occur in practice. Example: Intransitive decisions (Plous, 1993): You have to choose between the three job applicants: Applicant A B C Dimensions Intelligence Experience (in (IQ) years) 120 1 110 2 100 3

Biases and Paradoxes of human decision making Intransitivity of Preferences: Example: Intransitive decisions (Plous, 1993): You have to choose between the three job applicants: Applicant A B C Dimensions Intelligence Experience (in (IQ) years) 120 1 110 2 100 3 Assume that you conform to the following decision rule that sounds quite plausible: If the difference in IQ is greater than 10, then prefer the applicant with the higher IQ, otherwise prefer the one with more experience.

Biases and Paradoxes of human decision making Intransitivity of Preferences: Example: Intransitive decisions (Plous, 1993): Applicant A B C Dimensions Intelligence Experience (in (IQ) years) 120 1 110 2 100 3 If the difference in IQ is greater than 10, then prefer the applicant with the higher IQ, otherwise prefer the one with more experience. This results in the following preferences: , , and.
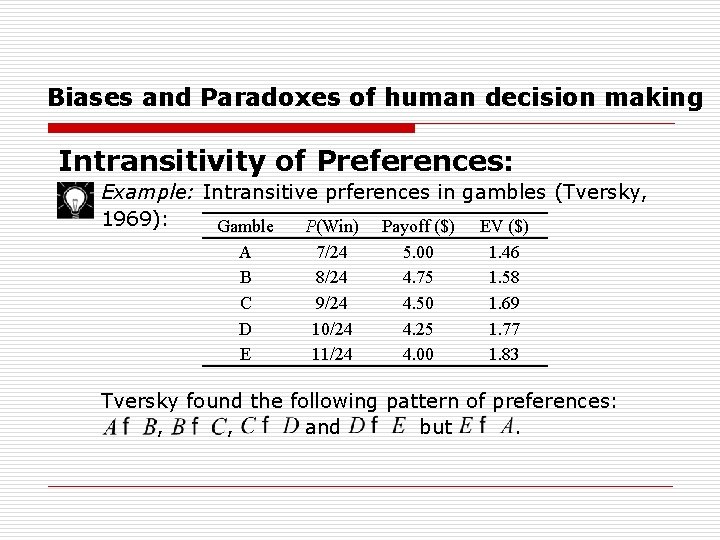
Biases and Paradoxes of human decision making Intransitivity of Preferences: Example: Intransitive prferences in gambles (Tversky, 1969): Gamble P(Win) Payoff ($) EV ($) A B C D E 7/24 8/24 9/24 10/24 11/24 5. 00 4. 75 4. 50 4. 25 4. 00 1. 46 1. 58 1. 69 1. 77 1. 83 Tversky found the following pattern of preferences: , , and but.
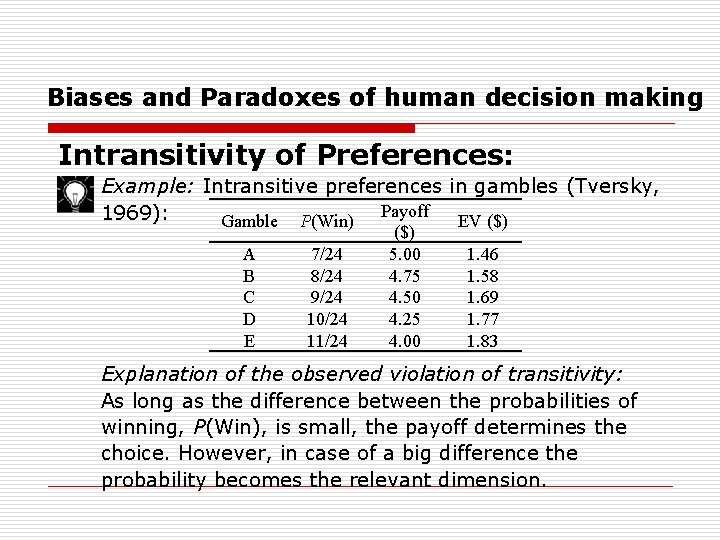
Biases and Paradoxes of human decision making Intransitivity of Preferences: Example: Intransitive preferences in gambles (Tversky, Payoff 1969): Gamble P(Win) EV ($) A B C D E 7/24 8/24 9/24 10/24 11/24 ($) 5. 00 4. 75 4. 50 4. 25 4. 00 1. 46 1. 58 1. 69 1. 77 1. 83 Explanation of the observed violation of transitivity: As long as the difference between the probabilities of winning, P(Win), is small, the payoff determines the choice. However, in case of a big difference the probability becomes the relevant dimension.

Biases and Paradoxes of human decision making Intransitivity of Preferences: Example: Committee Problem (Plous, 1993): q Given: 3 candidates for the job of a new professor: Newton, Einstein, and Feynman. q The faculty committee taking the decision consists of 5 members: Ann, Bob, Cindy, Dan, and Eric, with different preferences: Members of the committee Candidate Ann Bob Cindy Dan Eric Newton 1 1 2 3 3 Einstein 2 3 3 1 1 Feynman 3 2 1 2 2

Biases and Paradoxes of human decision making Intransitivity of Preferences: Example: Committee Problem (Plous, 1993): q Given: Members of the committee Candidate Ann Bob Cindy Dan Eric Newton 1 1 2 3 3 Einstein 2 3 3 1 1 Feynman 3 2 1 2 2 q This results in the following intransitive preferences: , , . q If the candidate is selected by means of a sequences of pair comparisons the order of the pair comparisons determines which candidate will be selected.

Biases and Paradoxes of human decision making Preference reversals: The relative preference for one alternative over another one should not depend on the way the preferences are elicited. Specifically, a decision maker preferring Option A over Option B should also be willing to pay a higher price for A than for B. Lichtenstein & Slovic (1971) found that this is not always the case.

Biases and Paradoxes of human decision making Preference reversals: Example: Preference reversals (Lichtenstein & Slovic, 1971): Given: The following pair of gambles: q Gamble A (Expected value: $3. 95): q Option 1: $4. 00 with probability. 99, q Option 2: $1. 00 with probability. 01. q Gamble B (Expected value: $3. 94): q Option 1: $16. 00 with probability. 33, q Option 2: $2. 00 with probability. 67. If people have the choice between Gamble A and B most choose A. However, people are willing to pay higher bids to play Gamble B than Gamble A.

Biases and Paradoxes of human decision making Preference reversals: Example: Preference reversals (Lichtenstein & Slovic, 1971): q This reversal was found for 73% of the participants. The result was replicated by Lichtenstein & Slovic (1973) with real gambles with 81% of the 44 gambler investigated exhibited the reversal. q Obviously, in case of choices, the probability of winning or loosing dominates the choice whereas in case of bidding the height of the payoff of the games is more important for determining the height of the bids.

Biases and Paradoxes of human decision making Preference reversals: q Preference reversals have also be found in case of joint versus separate evaluation of alternatives (Hsee, Loewen stein, Blount, & Bazerman, 1999). q In this case it is not the way, how the preferences are elicited as in the study of Lichtenstein & Slovic (1971) but whether the two alternatives are evaluated jointly ore separately.

Biases and Paradoxes of human decision making Preference reversals: Example: Preference Reversal with joint and separate evaluations (Hsee, Loewenstein, Blount, & Bazerman, 1999): q Two candidates for computer programmers in the language KY (a rarely use programming language): q Candidate J: q Experience: Has written 70 KY programs in last 2 years. q GPA (Grade point average): 3. 0. q Candidate S: q Experience: Has written 10 KY programs in last 2 years. q GPA (Grade point average): 4. 9.

Biases and Paradoxes of human decision making Preference reversals: Example: Preference Reversal with joint and separate evaluations (Hsee, Loewenstein, Blount, & Bazerman, 1999): q Candidate J: q Experience: Has written 70 KY programs in last 2 years. q GPA (Grade point average): 3. 0. q Candidate S: q Experience: Has written 10 KY programs in last 2 years. q GPA (Grade point average): 4. 9. The willingness to pay as salary (per year) for the two candidates was: Joint evaluation: J: $33, 200; S: $31, 200. Separate evaluation: J: $26, 800; S: $32, 700.

Biases and Paradoxes of human decision making Preference reversals: Preference Reversal with joint and separate evaluations: Explanation: Evaluability hypothesis q Some attributes are more difficult to evaluate than others. By consequence, if options are evaluated separately these attributes have little influence. If, however, options are evaluated jointly these attributes gain strength since a direct comparison between options on the respective attribute is possible. q In the given example, it is difficult to evaluate the utility of 10 or 70 hours of experience in KY programing. However, if compared directly it is obvious that Candidate J has considerably more experience than S.

Biases and Paradoxes of human decision making Preference reversals: Preference Reversal with joint and separate evaluations: Explanation: evaluability hypothesis q Consequently, when evaluated in isolation the simpler to evaluate attribute GPA gets a higher weight due to the fact that it is difficult to tell what 10 (or 70) hours of programming experience in this very particular programming language really means. With joint evaluation it becomes clear that Candidate J has considerably more experience than S.

Biases and Paradoxes of human decision making Preference reversals: Preference reversal can be the result of seemingly » irrele vant « aspects of the decision process: Preference Reversal between sequential and non sequential decisions (Kahneman & Tversky, 1979): Given: 2 scenarios: Scenario N: Choice between two options: Option A: $4, 000 with probability 0. 20. Option B: $3, 000 with probability 0. 25. Scenario S: A two stage game with two independent stages: q Stage 1: A probability of 0. 75 that the game ends without winning anything. q Stage 2: Choice between two options: Option A: $4, 000 with probability 0. 80. Option B: $3, 000 for sure (p = 1. 0).

Biases and Paradoxes of human decision making Preference reversals: Preference Reversal between sequential and non sequential decisions (Kahneman & Tversky, 1979): Given: 2 scenarios: q People prefer Option A in Scenario N (65%) and Option B in Scenario S (78%). q The final outcomes in the two scenarios are exactly the same: Since the probabilities are independent, the proba bility of winning $4, 000 in Scenario S is 0. 80 0. 25 = 0. 20, and the probability of winning $3, 000 in Scenario S is 1. 0 0. 25 = 0. 25. This corresponds exactly to the outcomes of Scenario N.

Biases and Paradoxes of human decision making Preference reversals: q Kahneman & Tversky (1979) explain the difference by the application of editing processes that are used to simplify the representations of decision options. q One of these editing processing consist in the cancellation of components that are shared by all alternatives. In particu lar, in Scenario S people cancel the first stage that is identi cal for both options. q This leaves a choice between getting $3, 000 for sure or gaining $4, 000 with probability 0. 80. Due to peoples’ risk aversive ness the certain option is selected. By contrast, in Scenario N the participants has a choice between two uncertain alternatives. Since the difference in probabilities is low, the game with the higher outcome is chosen.

Biases and Paradoxes of human decision making Preference reversals: Preference reversal can be the result of seemingly » irrele vant « aspects of the decision process: Preference Reversal and Point of Reference of Evaluation (Kahneman & Tversky, 1979): Given: 2 scenarios: Scenario G(ain): The participant gets a bonus or $1, 000 and faces the following decision situation: Option A: Getting $1, 000 with probability 0. 50. Option B: Getting $500 for sure. Scenario L(oss): The participant gets a bonus or $2, 000 and faces the following decision situation: Option C: Losing $1, 000 with probability 0. 50. Option D: Losing $500 for sure.

Biases and Paradoxes of human decision making Preference reversals: Preference reversal can be the result of seemingly » irrele vant « aspects of the decision process: Preference Reversal and Point of Reference of Evaluation (Kahneman & Tversky, 1979): q People prefer Option B in Scenario G (84%) and Option C in Scenario L (69%). q Again, the final outcomes in the two scenarios are exactly the same: A = C: Gaining $2, 000 or $1, 000, each with pro bability 0. 50. q Similarly B = D: Gaining $1, 500 for sure versus gaining $2, 000 or 1, 000, each with probability of 0. 50.

Biases and Paradoxes of human decision making Preference reversals: q According to Kahneman and Tversky (1979) the difference in preferences is due to the fact that in Scenario G the options represent gains whereas in Scenario L they represent losses. q Specifically, in evaluating the scenarios, people are first cancelling the bonus since it applies to both options (in both scenarios). q This results in decision of a sure gain of $500 in Scenario G and a sure loss of $500 in Scenario L. q Since people are risk aversive they prefer the sure gain in Scenario G and avoid the sure loss in Scenario L.

Biases and Paradoxes of human decision making Preference reversals: The example also demonstrates that the way how one arrives at a final outcome is important. Assume a final outcome of $100, 000. The subjective value of this outcome differs according to whether this outcome is attained by a loss of $5, 000 (i. e. a reduction of a previous wealth of $105, 000) or a gain of $5, 000 (i. e. an increase of the initial wealth of $95, 000). As a result, prospect theory (cf. Chapter 5. 4) assumes that subjective value functions are defined on gains and losses and not on absolute wealth.

Biases and Paradoxes of human decision making Less is more effect: Sometimes people are more willing to pay money for a worse alternative than for the better one. This has been named the less is more effect. Example: Less is more effect in different groups of cognitive ability (Stanovich & West, 2008): Participants receive one of three possible version of the following problem:

Biases and Paradoxes of human decision making Less is more effect: Example: Less is more effect (Stanovich & West, 2008): Form A: Imagine that highway safety experts have determined that a substantial number of people are at risk of dying in a type of automobile fire. A requirement that every car have a built in fire extinguisher (estimated cost, $300) would save the 150 people who would otherwise die every year in this type of automobile fire. Rate the following statement for yourself: I would be extremely supportive of this requirement. Form B: The term 150 people was replaces by 98% of 150 people. Form C: The term 150 people was replaces by 95% of 150 people.
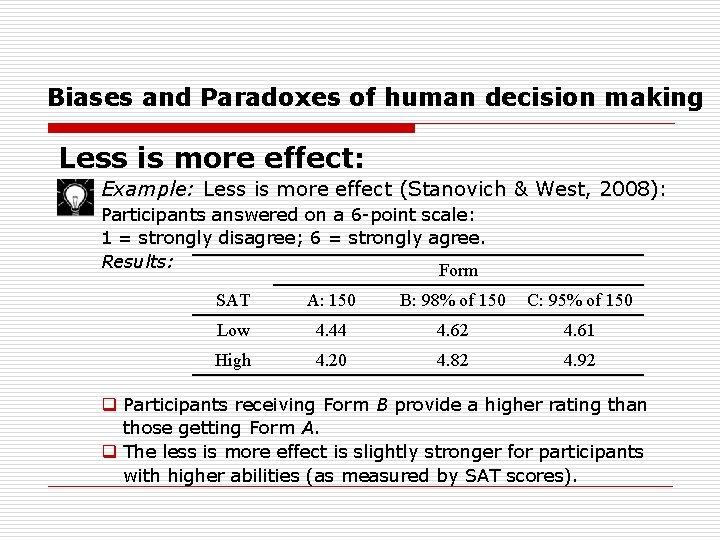
Biases and Paradoxes of human decision making Less is more effect: Example: Less is more effect (Stanovich & West, 2008): Participants answered on a 6 point scale: 1 = strongly disagree; 6 = strongly agree. Results: Form SAT A: 150 B: 98% of 150 C: 95% of 150 Low 4. 44 4. 62 4. 61 High 4. 20 4. 82 4. 92 q Participants receiving Form B provide a higher rating than those getting Form A. q The less is more effect is slightly stronger for participants with higher abilities (as measured by SAT scores).

Biases and Paradoxes of human decision making Decision Diversification: Decision diversification consists in the fact that with repeated choices people do not always choose the same (optimal) alternative but tend to choose different alternatives (they diversify their choices). Example: Decision diversification (Rubinstein, 2002): There is a deck of 100 cards that is composed as follows: q 36 cards are green (G). q 25 cards are green (B). q 22 cards are yellow (Y). q 17 cards are red (R) [original: brown]. 5 cards are drawn at random and put into 5 separate en velopes A, B, C, D, E.

Biases and Paradoxes of human decision making Decision Diversification: Example: Decision diversification (Rubinstein, 2002): There is a deck of 100 cards that is composed as follows: q 36 cards are green (G). q 25 cards are green (B). q 22 cards are yellow (Y). q 17 cards are red (R) [original: brown]. 5 cards are drawn at random and put into 5 separate en velopes A, B, C, D, E. Imagine that you receive a price for predicting the correct color of the card in each envelope. What would you predict for the different envelopes? Result: 42% (Study 1) and 38% (Study 2) of the participants made the optimal prediction: Green for each of the 5 envelopes.

Biases and Paradoxes of human decision making Decision Diversification: Example: Decision diversification (Rubinstein, 2002): Results: q 42% (Study 1) and 38% (Study 2) of the participants made the optimal prediction: Green for each of the 5 envelopes. q The other participants used a diversification strategy. q About 30% of the participants used Probability Matching (about 50% of participants who diversified). Comment: Please note that even with sampling without replacement, the probability of selecting the green card is greatest for each of the five draws.

Biases and Paradoxes of human decision making Decision Diversification: Example: Reduction of Decision diversification (Rubinstein, 2002): Imagine you are a detective in a shopping center. Every day a messenger arrives with an envelope. The center has 4 doors: G, B, Y, and R. The doors have different frequency of the messengers entering a door, specifically: q 36% of the messengers enter door G. q 25% of the messengers enter door B. q 22% of the messengers enter door Y. q 17% of the messengers enter door R. [original: brown]. You have to take photos of the messengers as they enter one of the doors for each of the 5 days of the week. However, you have only one camera that you can install each morning at one of the four gates. Which doors would you choose for each of the 5 days?

Biases and Paradoxes of human decision making Decision Diversification: Example: Reduction of Decision diversification (Rubinstein, 2002): Results: 70% (Study 1) and 72% (Study 2) of the participants always selected door G thus exhibiting optimal performance.

Decision Paradoxes In this section three famous paradoxes of human decision making are discussed: The St. Petersburg paradox, Ellsberg’s, and Allais’ paradox. St. Petersburg Paradox: The St. Petersburg Paradox was first mentioned by Nicolaus Bernoulli in 1713 and published by Daniel Bernoulli in 1738. Assume that someone offers you the following game: A coin is thrown until head (H) appears. Here is the gain you can get out of the game: q If H appears in the first throw you get Sfr. 1 (=20). q If H appears first with the second throw you get Sfr. 2 (=21). q If H appears first with the third throw you get Sfr. 4 (=22). q In general: If H appears for the first time one the n th throw you get Sfr. 2 n 1.

Decision Paradoxes St. Petersburg Paradox: Assume that someone offers you the following game: A coin is thrown until head (H) appears. Here is the gain you can get out of the game: q If H appears in the first throw you get Sfr. 1 (=20). q If H appears first with the second throw you get Sfr. 2 (=21). q If H appears first with the third throw you get Sfr. 4 (=22). q In general: If H appears for the first time one the n th throw you get Sfr. 2 n 1. How much money would you spend to be allowed to play this game? The paradox consists in the fact that the expected gain E of the game is infinite:

Decision Paradoxes St. Petersburg Paradox: Most people are not willing to spend much money (usually less than Sfr. 2) for being allowed to play the game. Explanations: 1. Diminishing return / Concave form of the utility function for gains: The utility of money diminishes with the general wealth of the individual. Thus, even if the amount of money gained may be infinite, its utility for the individual may be finite. The problem with this explanation consists in the fact that it cannot explain why people offer such a low amount of money for being allowed to play the game.

Decision Paradoxes St. Petersburg Paradox: Explanations: 2. Finite resources: No person or institution in the world can pay an infinite amount of money. Thus, no one can fulfill the requirements of the game. This explanation has the weakness that constraining the total a mount of money offered to, say, Sfr. 20, 000 does not increase the stack offered by participants. 3. Undefined expected value: The expectation E defined above is not infinite but undefined. Thus, the reluctance of participants to invest high sums is not irrational. This line of argument has a similar problem as the previous one:

Decision Paradoxes St. Petersburg Paradox: Explanations: 3. Undefined expected value: The expectation E defined above is not infinite but undefined. Thus, the reluctance of participants to invest high sums is not irrational. This line of argument has a similar problem as the previous one: Assume that we restrict the number of possible rounds to, say, 225 (assume that the game is played by a computer such that the maximal possible gain can be achieved within a view minutes). The expected value of this game is E = Sfr. 224 (=Sfr. 16, 777, 216). Nevertheless, this will not increase participants’ willingness to invest high sums.

Decision Paradoxes St. Petersburg Paradox: Explanations: 4. Low probability and risk aversion: This explanation is based on the observation that high gains occur only with long runs of heads and are thus quite improbable. Note that the expected number of trials is 2, i. e. the game ends, on average, after two trials. Since people are risk aversive they refrain from investing high stacks. 5. Utility of the mean and utilization of the median: The expectation is not useful due to the high skew of the distribution of outcomes. A more sensible measure is the median value which lies between 1 and 2, say, Sfr. 1. 5. Hayden and Platt (2009) found that the median value of the bids was also Sfr. 1. 5.

Decision Paradoxes Ellsberg’s Paradox: Ellsberg’s paradox has been proposed by Daniel Ellsberg in 1961. There are two versions of the paradox. Both demonstrate that people do not conform to the famous axioms of L. J. Savage (1917 1971). Ellsberg’s Paradox (Version with 2 colors): Given: Two urns, U 1 and U 2, both containing 100 balls. q U 1 contains exactly 50 red and 50 black balls. q The distribution of red and black balls in U 2 is unknown. People get the following sequence of decisions: 1. Bet on red 1 or black 1 or indifferent? 2. Bet on red 2 or black 2 or indifferent? 3. Bet on red 1 or red 2 or indifferent? 4. Bet on black 1 or black 2 or indifferent?

Decision Paradoxes Ellsberg’s Paradox (Version with 2 colors): Given: Two urns, U 1 and U 2, both containing 100 balls. q U 1 contains exactly 50 red and 50 black balls. q The distribution of red and black balls in U 2 is unknown. People get the following sequence of decisions: 1. Bet on red 1 or black 1 or indifferent? 2. Bet on red 2 or black 2 or indifferent? 3. Bet on red 1 or red 2 or indifferent? 4. Bet on black 1 or black 2 or indifferent? The modal choice pattern is the following: 1. indifferent 2. indifferent 3. red 1 4. black 1

Decision Paradoxes Ellsberg’s Paradox (Version with 2 colors): The modal choice pattern: 1. indifferent 2. indifferent 3. red 1 4. black 1 This pattern demonstrates that people are predominantly aver sive against ambiguity. However, the pattern of choices is not consist ent, for the following reason: Preferring red 1 over red 2 in the third choice amounts to the assumption that P(red 1) > P(red 2), or, equivalently, P(black 1) < P(black 2). The preference for black 1 over black 2 in the fourth choice is thus inconsistent.
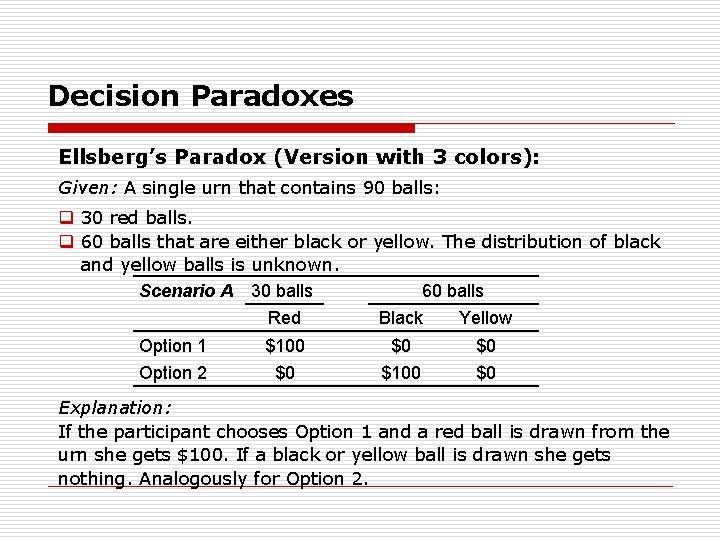
Decision Paradoxes Ellsberg’s Paradox (Version with 3 colors): Given: A single urn that contains 90 balls: q 30 red balls. q 60 balls that are either black or yellow. The distribution of black and yellow balls is unknown. Scenario A 30 balls 60 balls Red Black Yellow Option 1 $100 $0 $0 Option 2 $0 $100 $0 Explanation: If the participant chooses Option 1 and a red ball is drawn from the urn she gets $100. If a black or yellow ball is drawn she gets nothing. Analogously for Option 2.
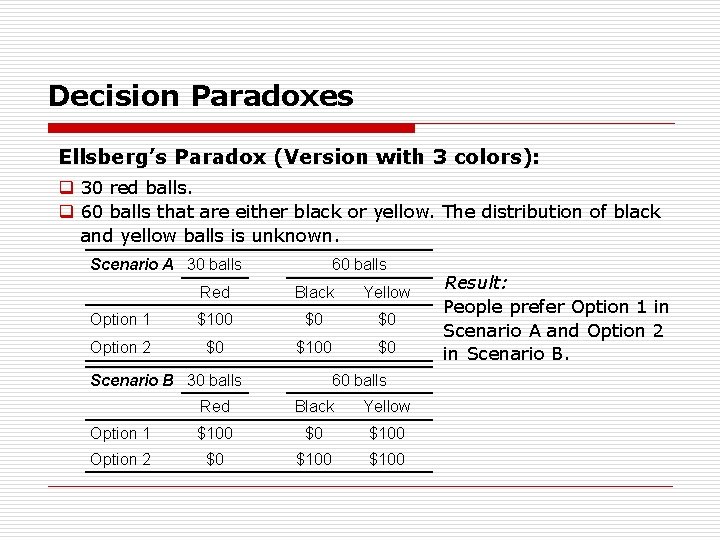
Decision Paradoxes Ellsberg’s Paradox (Version with 3 colors): q 30 red balls. q 60 balls that are either black or yellow. The distribution of black and yellow balls is unknown. Scenario A 30 balls 60 balls Red Black Yellow Option 1 $100 $0 $0 Option 2 $0 $100 $0 Scenario B 30 balls 60 balls Red Black Yellow Option 1 $100 $0 $100 Option 2 $0 $100 Result: People prefer Option 1 in Scenario A and Option 2 in Scenario B.
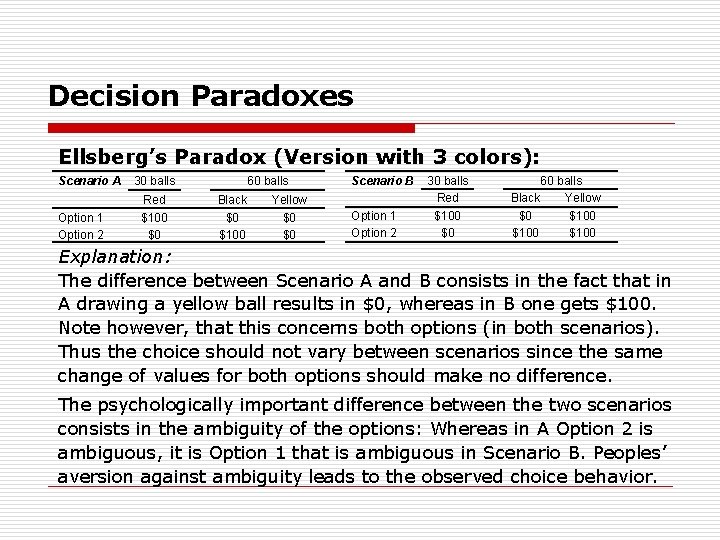
Decision Paradoxes Ellsberg’s Paradox (Version with 3 colors): Scenario A Option 1 Option 2 30 balls 60 balls Red Black Yellow $100 $0 $0 Scenario B Option 1 Option 2 30 balls Red $100 $0 60 balls Black Yellow $0 $100 Explanation: The difference between Scenario A and B consists in the fact that in A drawing a yellow ball results in $0, whereas in B one gets $100. Note however, that this concerns both options (in both scenarios). Thus the choice should not vary between scenarios since the same change of values for both options should make no difference. The psychologically important difference between the two scenarios consists in the ambiguity of the options: Whereas in A Option 2 is ambiguous, it is Option 1 that is ambiguous in Scenario B. Peoples’ aversion against ambiguity leads to the observed choice behavior.

Decision Paradoxes The Allais Paradox: The Allais paradox was presented in 1953 by the French economist Maurice Allais (1911 2010). It demonstrates peoples’ preference for certainty. However, this preference leads to violations of normative principles. Certainty effect and Allais paradox (Kahneman, 2011): Consider the following 2 decision problems. How would you decide? Problem I: Option A: Option B: A gain of Sfr. 520 000. - with probability p = 0. 61 or winning nothing with probability p = 0. 39. A gain of Sfr. 500 000. - with probability p = 0. 63 or winning nothing with probability p = 0. 37.
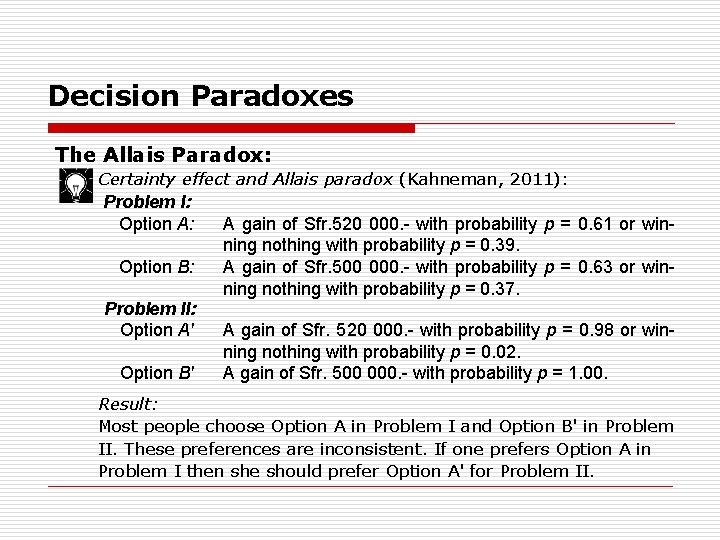
Decision Paradoxes The Allais Paradox: Certainty effect and Allais paradox (Kahneman, 2011): Problem I: Option A: Option B: Problem II: Option A' Option B' A gain of Sfr. 520 000. - with probability p = 0. 61 or winning nothing with probability p = 0. 39. A gain of Sfr. 500 000. - with probability p = 0. 63 or winning nothing with probability p = 0. 37. A gain of Sfr. 520 000. - with probability p = 0. 98 or winning nothing with probability p = 0. 02. A gain of Sfr. 500 000. - with probability p = 1. 00. Result: Most people choose Option A in Problem I and Option B' in Problem II. These preferences are inconsistent. If one prefers Option A in Problem I then she should prefer Option A' for Problem II.

Decision Paradoxes The Allais Paradox: Certainty effect and Allais paradox (Kahneman, 2011): Problem I: Option A: Option B: Problem II: Option A' Option B' A gain of Sfr. 520 000. - with probability p = 0. 61 or winning nothing with probability p = 0. 39. A gain of Sfr. 500 000. - with probability p = 0. 63 or winning nothing with probability p = 0. 37. A gain of Sfr. 520 000. - with probability p = 0. 98 or winning nothing with probability p = 0. 02. A gain of Sfr. 500 000. - with probability p = 1. 00. One can illustrate the chances of winning in Problem I by means of two urns, A and B, representing the two options: q Urn A contains 61 balls labeled 520, 000 and 39 balls labeled 0. q Urn B contains 63 balls labeled 500, 000 und 37 balls with the label 0. The options of Problem II result from those of I by replacing 37 balls of Urn A labeled 0 with 37 balls labeled 520, 000 (resulting in Urn A’), and by replacing 37 balls of Urn B labeled 0 with 37 balls labeled 500, 000 (resulting in Urn B’).

Decision Paradoxes The Allais Paradox: Certainty effect and Allais paradox (Kahneman, 2011): One can illustrate the chances of winning in Problem I by means of two urns, A and B, representing the two options: q Urn A contains 61 balls labeled 520, 000 and 39 balls labeled 0. q Urn B contains 63 balls labeled 500, 000 und 37 balls with the label 0. The options of Problem II result from those of I by replacing 37 balls of Urn A labeled 0 with 37 balls labeled 520, 000 (resulting in Urn A’), and by replacing 37 balls of Urn B labeled 0 with 37 balls labeled 500, 000 (resulting in Urn B’). Obviously, the modification of Urn A is more valuable than that of B since for both the same number of balls has been replaced but the values of the single balls are higher for A than B: 520, 000 vs. 500, 000. Consequently, preferring A in Problem I should be accompanied by preferring A’ in Problem II.

Decision Paradoxes The Allais Paradox: Explanation: Certainty effect and Allais paradox The reason for the observed inconsistency of peoples choices consists in the fact that Option B‘ in Problem II permits a sure (high) gain. For this gain people are willing to accept a lower return. This is called a certainty effect. Peoples’ decisions are driven by their desire by to avoid regret (and anger) that would result in case of a negative outcome for Urn A’. Allais paradox contradicts Subjective Expected Utility (SEU) theory which is easily demonstrated. Peoples’ preferences for Problem I can be represented by the inequality: Where u() represents the subjective utility of the respective amount of money.

Decision Paradoxes The Allais Paradox: Explanation: Certainty effect and Allais paradox contradicts Subjective Expected Utility (SEU) theory which is easily demonstrated. Peoples’ preferences for Problem I can be represented by the inequality: This inequality can be transformed to: Peoples’ preferences for Problem II can be represented by the inequality: This inequality can be transformed to: Obviously, both inequalities cannot be true at the same time.

Decision Paradoxes The Allais Paradox: The certainty effect and insurances: The certainty effect influences the acquisition of insurances against damages since people prefer assurances that provide perfect security. One important consequence of this behavior consists in the fact that people pay too high health insurance rates. For example, most people in Switzerland are paying too high health insurance rates by choosing a franchise too low. People ignore the fact that insurances never provide a perfect protection since they are quite specific: A fire insurance protects against damages due to fire and a windstrom insurance helps only in case of damages due to tornados.
- Slides: 79