Bi ging Ton 12 H TO TRONG KHNG

Bài giảng Toán 12 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN

KIỂM TRA BÀI CŨ: Câu 1: Em hãy nêu định nghĩa trục toạ độ? Câu 2: Em hãy nêu định nghĩa hệ trục toạ độ trong mặt phẳng? Trả lời: Câu 1: Trục toạ độ là một đường thẳng trên đó đã xác định một điểm O gọi là điểm gốc và một véc tơ đơn vị Ký hiệu: x’ I x Ta lấy điểm I sao cho. Tia OI còn được ký hiệu là Ox, tia đối của Ox là Ox’. Khi đó trục còn gọi là trục x’Ox hay trục Ox.

KIỂM TRA BÀI CŨ: Câu 2: Em hãy nêu định nghĩa hệ trục toạ độ trong mặt phẳng? Trả lời: Hệ trục toạ độ gồm hai trục và vuông góc với nhau. Điểm gốc O của hai trục gọi là gốc toạ độ. Trục gọi là trục hoành, kí hiệu là Ox. Trục gọi là trục tung, kí hiệu là Oy. Các vectơ Hệ trục toạ độ là các vectơ đơn vị trên Ox và Oy và còn được kí hiệu là Oxy. Chú ý: Mặt phẳng trên đó đã cho một hệ trục toạ độ Oxy được gọi là mặt phẳng Oxy y . Oy là trục tung x Điểm O là gốc toạ độ Ox là trục hoành

CHƯƠNG III PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN v. Hệ toạ độ trong không gian v. Phương trình mặt phẳng v. Phương trình đường thẳng Trụ sở liên hợp quốc tại New York

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. 1) Hệ toạ độ : Định nghĩa (SGK) Ký hiệu: Oxyz. z’Oz là trục cao Điểm O là gốc toạ độ +) Điểm O được gọi là gốc toạ độ. +) Trục x’Ox được gọi là trục hoành. +) Trục y’Oy được gọi là trục tung. +) Trục z’Oz được gọi là trục cao. +) , , là ba véc tơ đơn vị đôi một vuông góc, ta có: z x’ O y y’ z’ +) Các mặt phẳng toạ độ (Oxy), (Oyz), (Ozx). +) Không gian với hệ toạ độ Oxyz còn được gọi là không gian Oxyz. x x’Ox là trục hoành y’Oy là trục tung

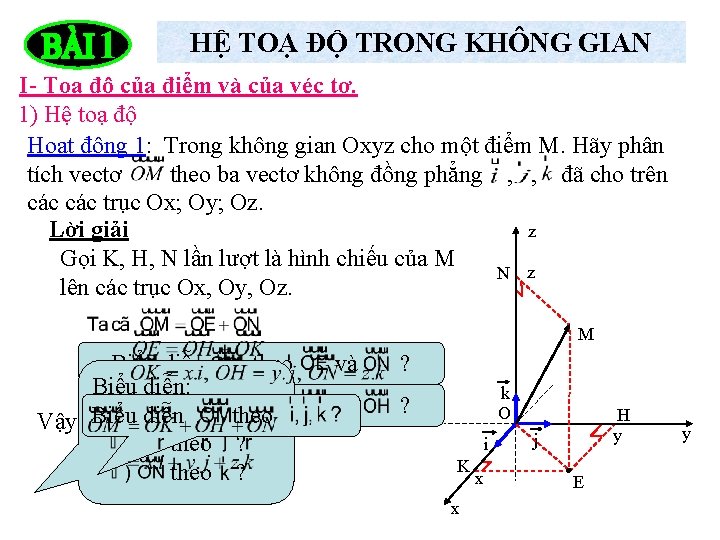
1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. 1) Hệ toạ độ Hoạt động 1: Trong không gian Oxyz cho một điểm M. Hãy phân tích vectơ theo ba vectơ không đồng phẳng , , đã cho trên các trục Ox; Oy; Oz. Lời giải z Gọi K, H, N lần lượt là hình chiếu của M N z lên các trục Ox, Oy, Oz. M Biểu diễn theo Biểu diễn: Biểu diễn theo ? Biểu diễn theo Vậy theo ? và và ? k O ? i K x x H y j E y

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. 2) Toạ độ của một điểm. ĐN: Bộ ba số thực (x; y; z) thoả mãn gian Oxyz cho gọi là Trong toạ độkhông của điểm đối hệcó trục toạ độ Oxyz. Với bộ 3 Msố (x; với y; z) điểm M và 3 nhiêu vectơ Viết M(x; y; z) hoặc M= (x; y; z). z bao điểm M thoả không đồng mãnphẳng. Có bao z N nhiêu bộ 3 số (x; y; z) thoả Nhận xét: x; y; z là toạ độ tương ứng của các mãn: điểm K; H; N. Trên các trục toạ độ Ox, Oy, Oz O i K x x M k H y j E y

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. 2) Toạ độ của một điểm. Ví dụ 1: Trong không gian với hệ toạ độ Oxyz. Xác định toạ độ của các điểm M, N? Giải: a) M(2; 5; -1); Vậy N(0; -1; 2)

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. Em hãy nêu định lý về biểu diễn một vectơ theo 3 vectơ không đồng phẳng?

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. 3. Toạ độ của véc tơ

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I- Toạ độ của điểm và của véc tơ. 3. Toạ độ của véc tơ Hoạt động 2: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD. A’B’C’D’ có đỉnh A trùng với gốc O, có theo thứ tự cùng hướng với và có AB = a, AD =b, AA’ = c. Hãy tính toạ độ các vectơ với M là trung điểm của C’D’. Giải: Ta có: A’ B’ B x z c A a O D’ C’ M D b y C

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN Kiến thức cũ Trong mặt phẳng với hệ trục toạ độ Oxy cho Ta có:

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN II- Biểu thức toạ độ của các phép toán vectơ Định lý: Trong không gian Oxyz cho hai vectơ Ta có: Hệ quả: +) Toạ độ trung điểm M của đoạn thẳng AB là :

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN Củng cố: Qua bài học cần nắm được các kiến thức trọng tâm sau: I- Toạ độ của điểm và của véc tơ. 1) Định nghĩa hệ toạ độ 2)Toạ độ của một điểm. II- Biểu thức toạ độ của các phép toán vectơ Định lý: Trong không gian Oxyz cho hai vectơ Ta có: Bộ ba số thực (x; y; z) thoả mãn gọi là toạ độ của điểm M đối với hệ trục toạ độ Oxyz. Viết M(x; y; z) hoặc M = (x; y; z). 3) Toạ độ của véc tơ Hệ quả:

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN Câu hỏi thảo luận Trong không gian với hệ toạ độ Oxyz Nhóm 1, 2: a) Tìm toạ độ của các véc tơ: Nhóm 3, 4: b)Xác định toạ độ trung điểm của đoạn thẳng BC CMR : Ba điểm A, B, C thẳng hàng. Đáp án: b) Toạ độ trung điểm M của đoạn thẳng BC là: Hai véc tơ cùng phương vì Vậy ba điểm A, B, C thẳng hàng.

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN Công việc về nhà: Ôn tập lý thuyết Làm bài tập 1, 2, 3 SGK trang 68 Nghiên cứu phần III, IV SGK.

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN Hệ trục tọa độ như ta đã học còn được gọi là hệ trục tọa độ Đêcac vuông góc, đó là tên của nhà toán học phát minh ra nó. Một vài nét về nhà toán học Đêcac (Descartes) sinh ngày 31/03/1596 tại Pháp và mất ngày 11/02/1650 tại Thụy Điển. Đêcac đã có rất nhiều đóng góp cho toán học. Ông đã sáng lập ra môn hình học giải tích. Cơ sở của môn này là phương pháp toạ độ do ông phát minh. Nó cho phép nghiên cứu hình học bằng ngôn ngữ và phương pháp của đại số. Các phương pháp toán học của ông đã có ảnh hưởng sâu sắc đến sự phát triển của toán học và cơ học sau này.

1 HỆ TOẠ ĐỘ TRONG KHÔNG GIAN Một vài nét về nhà toán học Đêcac 17 năm sau ngày mất , ông được đưa về Pháp và chôn cất tại nhà thờ mà sau này trở thành điện Păngtêông(Panthéon), nơi yên nghỉ của các danh nhân nước Pháp. Tên của Đêcác được đặt tên cho một miệng núi lửa trên phần trông thấy của mặt trăng.

XIN CH N THÀNH CÁM ƠN CÁC THẦY CÔ GIÁO VÀ CÁC EM HỌC SINH XIN CH N THÀNH CẢM ƠN CÁC THẦY (CÔ) VÀ CÁC EM HỌC SINH Xin chào và hẹn gặp lại !