BI GING MN TON 9 CH T GIC

BÀI GIẢNG MÔN TOÁN 9 CHỦ ĐỀ : TỨ GIÁC NỘI TIẾP Giáo viên thực hiện: Đỗ Thị Huyên
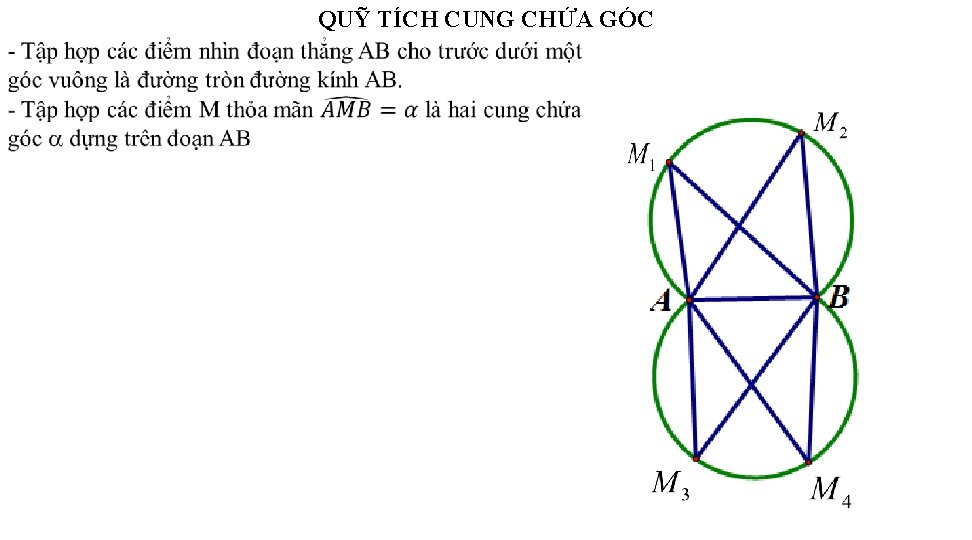
QUỸ TÍCH CUNG CHỨA GÓC
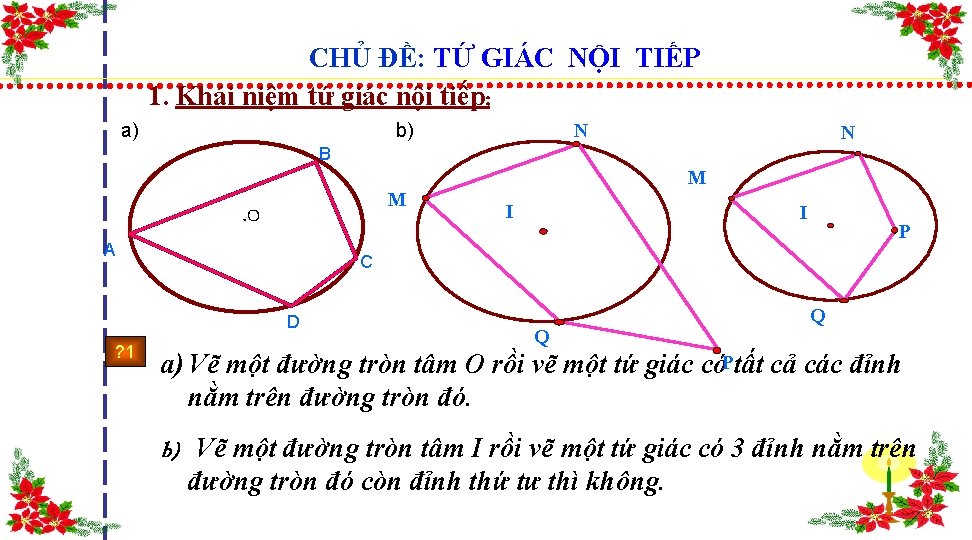
CHỦ ĐỀ: TỨ GIÁC NỘI TIẾP 1. Khái niệm tứ giác nội tiếp: a) b) N N B A M . O I I P C D ? 1 M Q Q a) Vẽ một đường tròn tâm O rồi vẽ một tứ giác cóPtất cả các đỉnh nằm trên đường tròn đó. b) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có 3 đỉnh nằm trên đường tròn đó còn đỉnh thứ tư thì không.
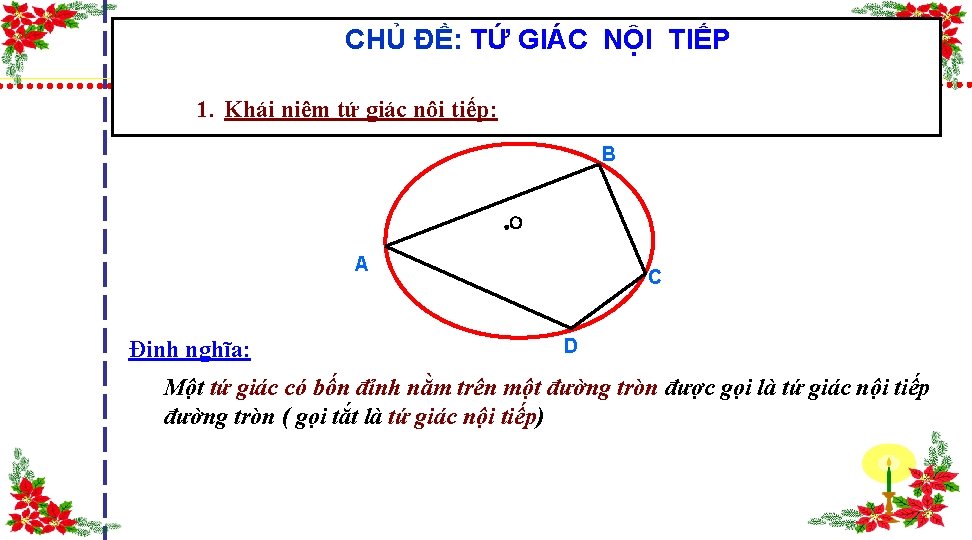
CHỦ ĐỀ: TỨ GIÁC NỘI TIẾP 1. Khái niệm tứ giác nội tiếp: B . O A Định nghĩa: C D Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn ( gọi tắt là tứ giác nội tiếp)
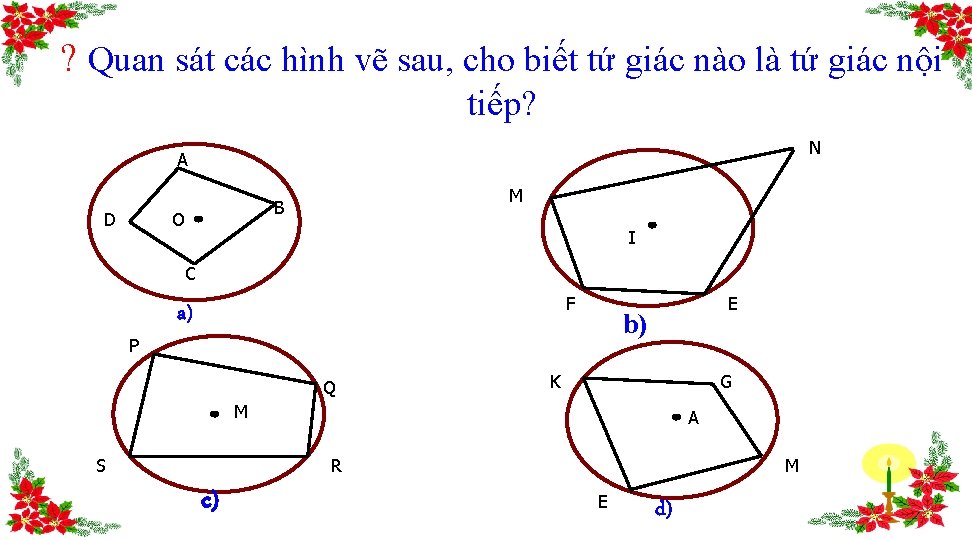
? Quan sát các hình vẽ sau, cho biết tứ giác nào là tứ giác nội tiếp? N A D M B O I C P F a) Q E b) K G M S A R c) M E d)

Hãy cho biết trong hình có bao nhiêu tứ giác nội tiếp đường tròn (O)? Yêu cầu: Tên mỗi tứ giác chỉ được liệt kê một lần. B A C O E D
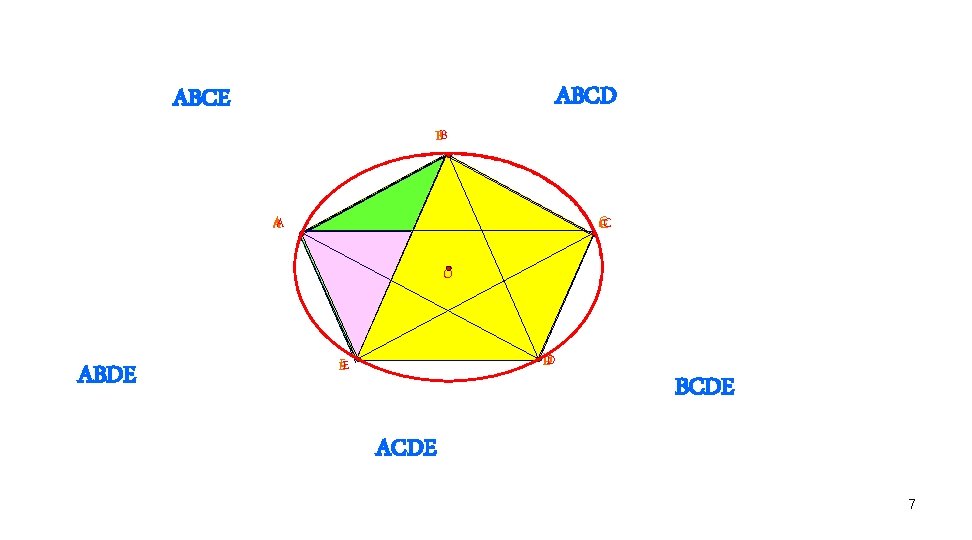
ABCD ABCE BB AA CC O ABDE DD EE BCDE ACDE 7

CHỦ ĐỀ: TỨ GIÁC NỘI TIẾP NỘI DUNG 1. Khái niệm tứ giác nội tiếp: Định nghĩa: 2. Định lý:
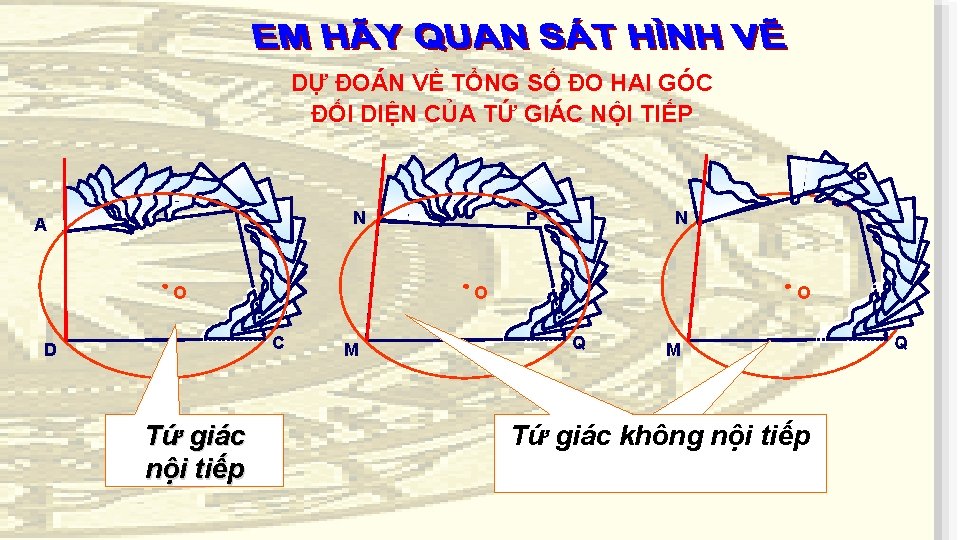
DỰ ĐOÁN VỀ TỔNG SỐ ĐO HAI GÓC ĐỐI DIỆN CỦA TỨ GIÁC NỘI TIẾP P B N A O O C D Tứ giác nội tiếp N P M O Q M Tứ giác không nội tiếp Q
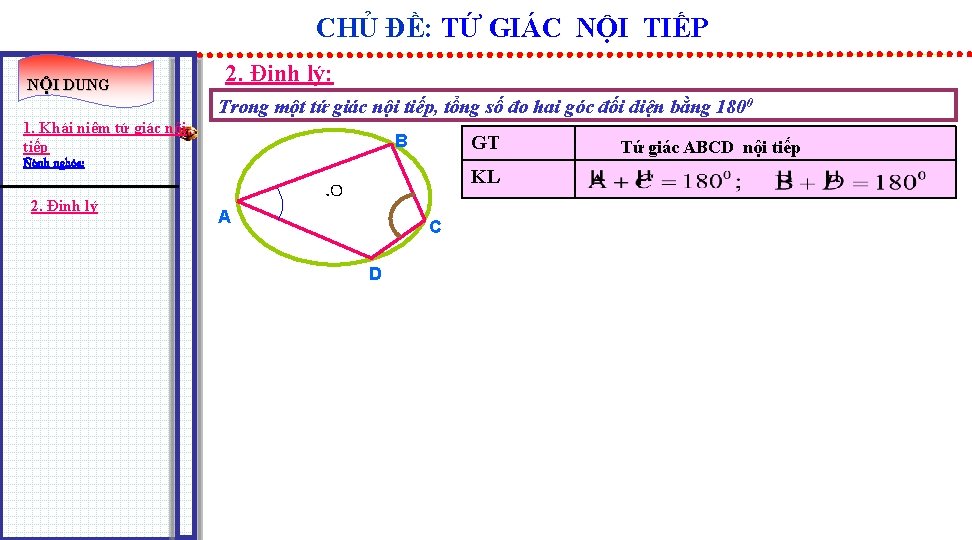
CHỦ ĐỀ: TỨ GIÁC NỘI TIẾP NỘI DUNG 2. Định lý: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 1800 1. Khái niệm tứ giác nội tiếp Ñònh nghóa: 2. Định lý B A GT KL . O C D Tứ giác ABCD nội tiếp
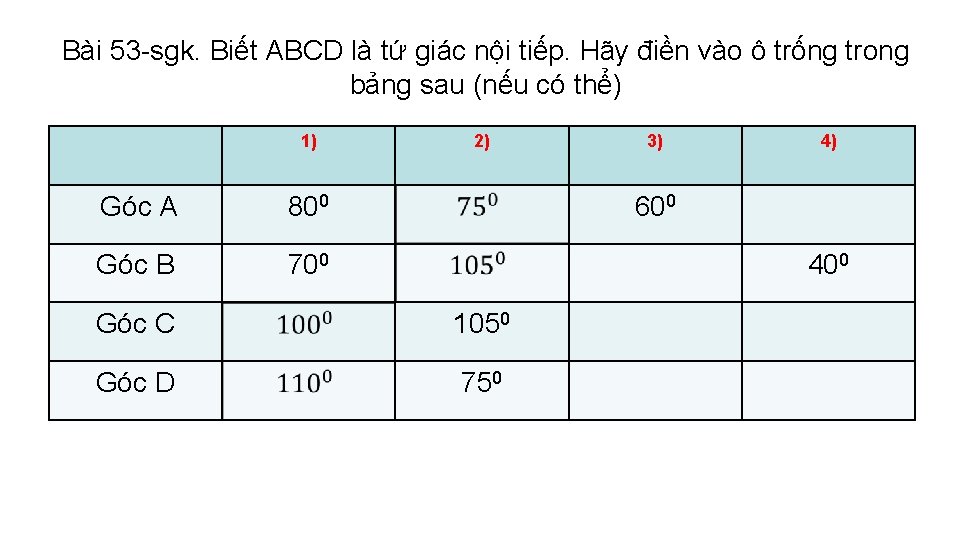
Bài 53 -sgk. Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bảng sau (nếu có thể) 1) Góc A 800 Góc B 700 2) 3) 4) 600 400 Góc C 1050 Góc D 750
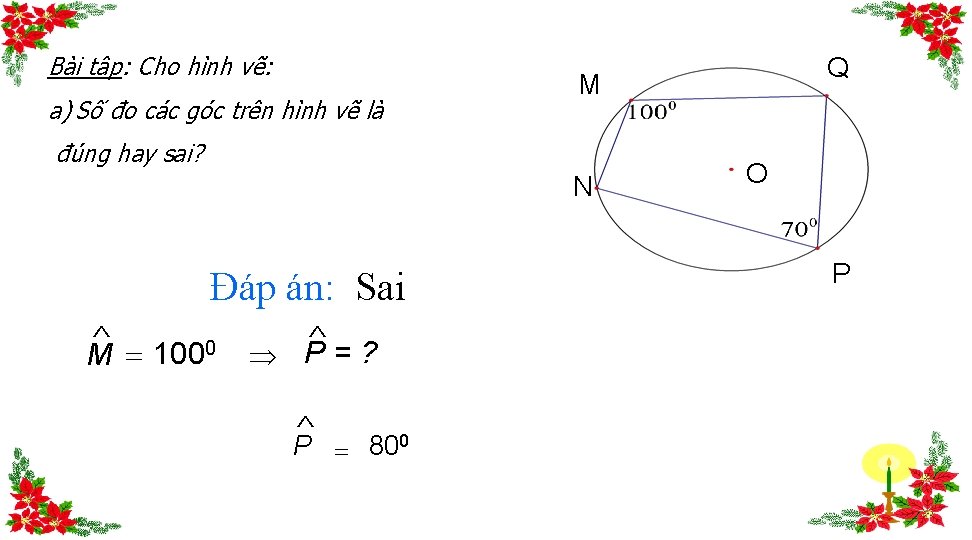
Bài tập: Cho hình vẽ: a) Số đo các góc trên hình vẽ là M đúng hay sai? N Đáp án: Sai ^ M = 1000 ^ P=? ^ P = 800 Q O P
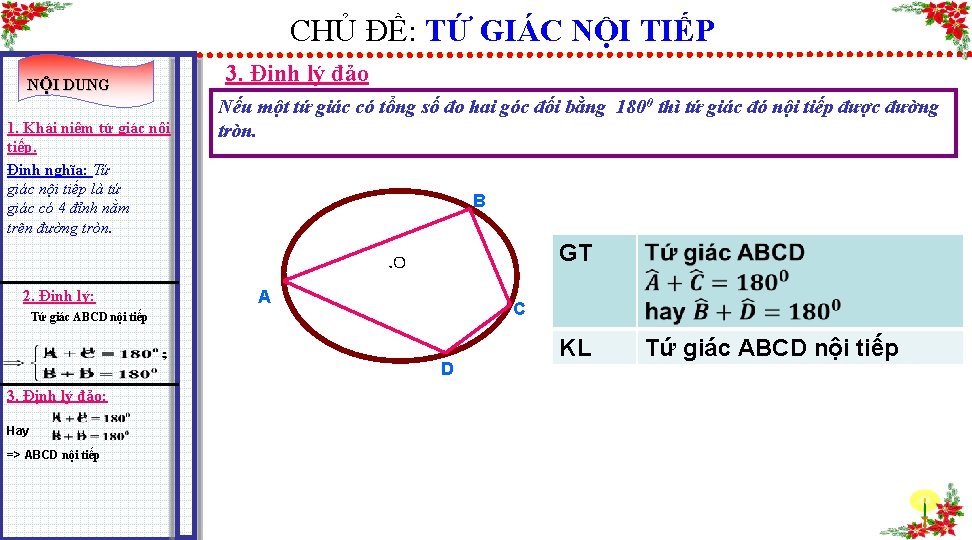
CHỦ ĐỀ: TỨ GIÁC NỘI TIẾP NỘI DUNG 1. Khái niệm tứ giác nội tiếp. Định nghĩa: Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên đường tròn. 2. Định lý: 3. Định lý đảo Nếu một tứ giác có tổng số đo hai góc đối bằng 1800 thì tứ giác đó nội tiếp được đường tròn. B A GT . O C Tứ giác ABCD nội tiếp D 3. Định lý đảo: Hay => ABCD nội tiếp KL Tứ giác ABCD nội tiếp
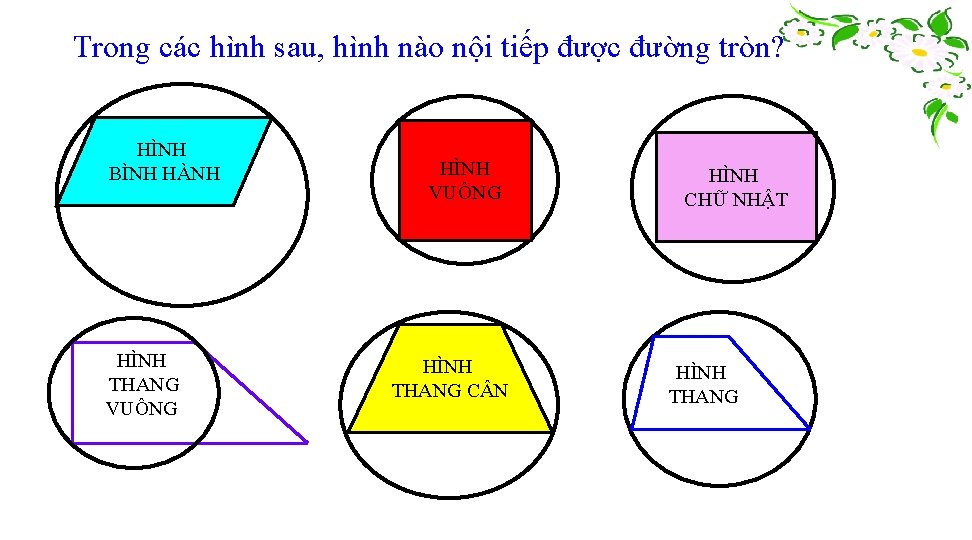
Trong các hình sau, hình nào nội tiếp được đường tròn? HÌNH BÌNH HÀNH HÌNH THANG VUÔNG HÌNH THANG C N HÌNH CHỮ NHẬT HÌNH THANG
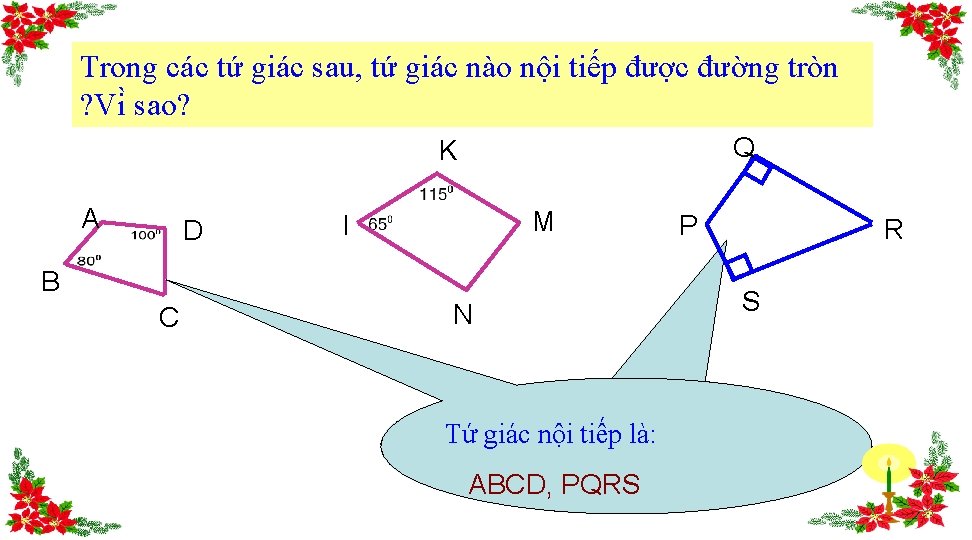
Trong các tứ giác sau, tứ giác nào nội tiếp được đường tròn ? Vi sao? Q K A D M I B C N Tứ giác nội tiếp là: ABCD, PQRS P R S
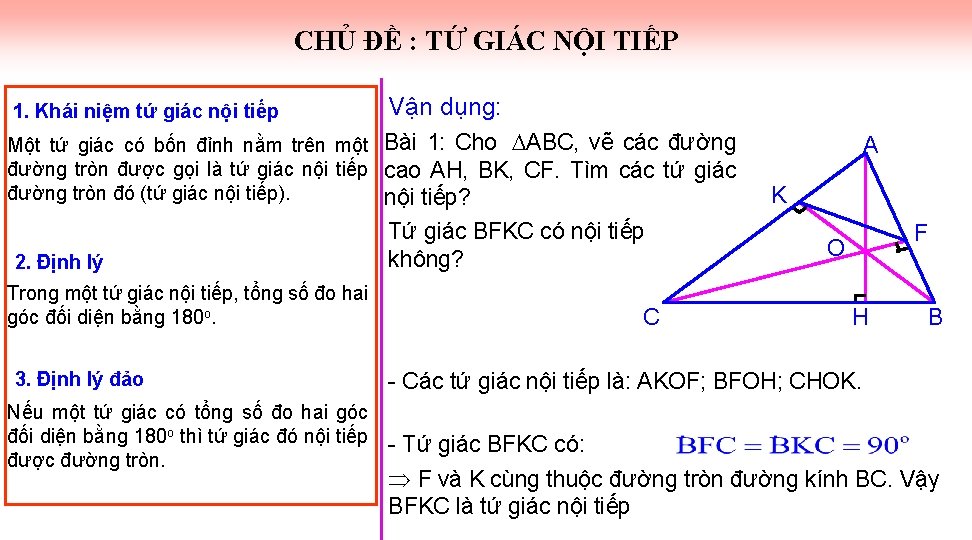
CHỦ ĐỀ : TỨ GIÁC NỘI TIẾP 1. Khái niệm tứ giác nội tiếp Vận dụng: Một tứ giác có bốn đỉnh nằm trên một Bài 1: Cho ABC, vẽ các đường tròn được gọi là tứ giác nội tiếp cao AH, BK, CF. Tìm các tứ giác đường tròn đó (tứ giác nội tiếp). nội tiếp? 2. Định lý Tứ giác BFKC có nội tiếp không? Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180 o. 3. Định lý đảo C A K F O H B - Các tứ giác nội tiếp là: AKOF; BFOH; CHOK. Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 o thì tứ giác đó nội tiếp - Tứ giác BFKC có: được đường tròn. F và K cùng thuộc đường tròn đường kính BC. Vậy BFKC là tứ giác nội tiếp

CHỦ ĐỀ : TỨ GIÁC NỘI TIẾP 1. Khái niệm tứ giác nội tiếp Vận dụng: A Một tứ giác có bốn đỉnh nằm trên một Bài 2: Cho hình vẽ. S là điểm đường tròn được gọi là tứ giác nội tiếp chính giữa cung AB. Chứng minh tứ giác EHCD nội tiếp đường tròn đó (tứ giác nội tiếp). Lời giải: 2. Định lý E B H O D Xét đường tròn (O) có: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180 o. (Góc có đỉnh ở bên trong đường tròn) (Góc nội tiếp đường tròn) 3. Định lý đảo Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 o thì tứ giác đó nội tiếp được đường tròn. S Mà (gt) nên C
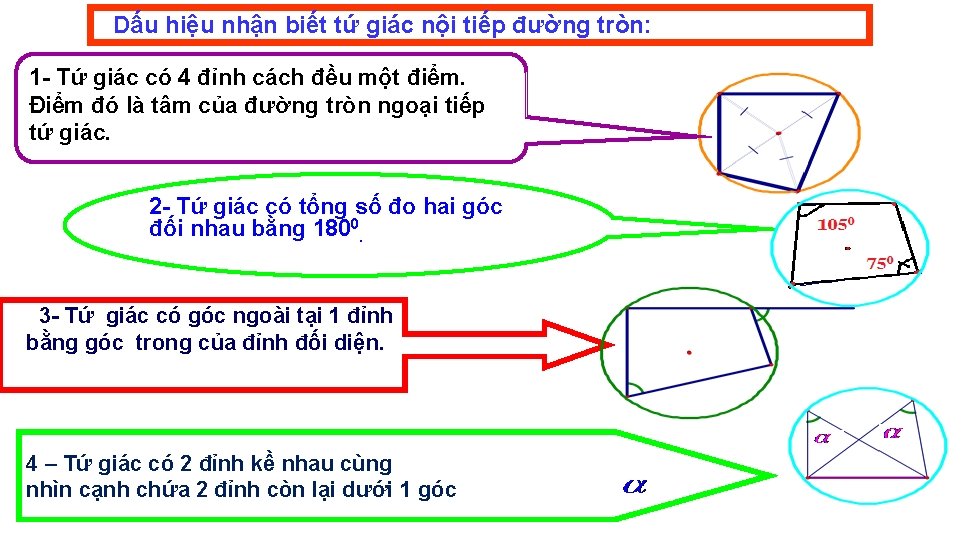
Dấu hiệu nhận biết tứ giác nội tiếp đường tròn: 1 - Tứ giác có 4 đỉnh cách đều một điểm. Điểm đó là tâm của đường tròn ngoại tiếp tứ giác. 2 - Tứ giác có tổng số đo hai góc đối nhau bằng 1800. 3 - Tứ giác có góc ngoài tại 1 đỉnh bằng góc trong của đỉnh đối diện. 4 – Tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới 1 góc
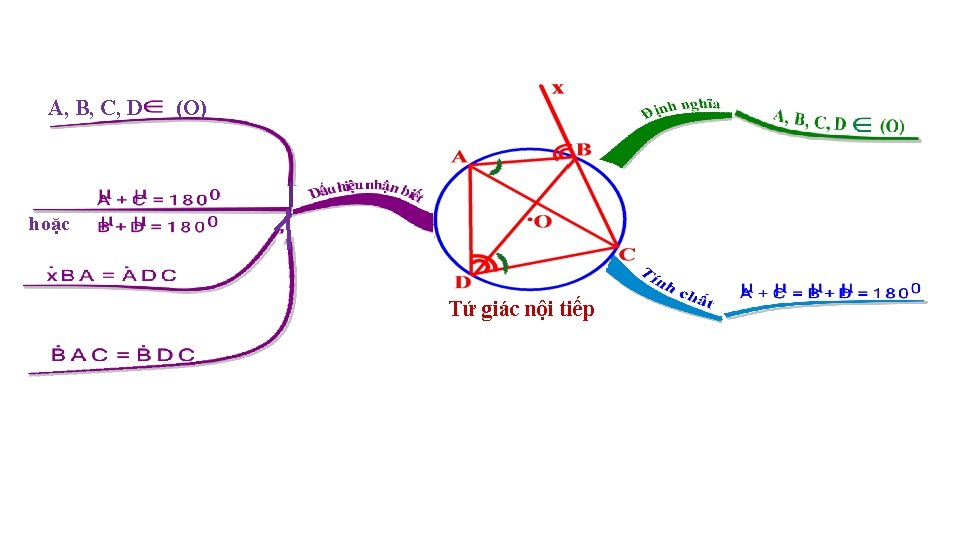
A, B, C, D (O) hoặc Tứ giác nội tiếp

HƯỚNG DẪN HỌC Ở NHÀ Kiến thức cần nhớ: 1. Thế nào là tứ giác nội tiếp 2. Tứ giác nội tiếp có tính chất gì? 3. Nếu cần chứng minh tứ giác nội tiếp ta cần chứng minh điều gì? (Dấu hiệu nhận biết ) Bài tập: Làm bài 55, 56, 58 SGK
- Slides: 20