Bi ging hnh hc lp 12 Khi a

Bài giảng hình học lớp 12 Khối đa diện lồi Khối đa diện đều

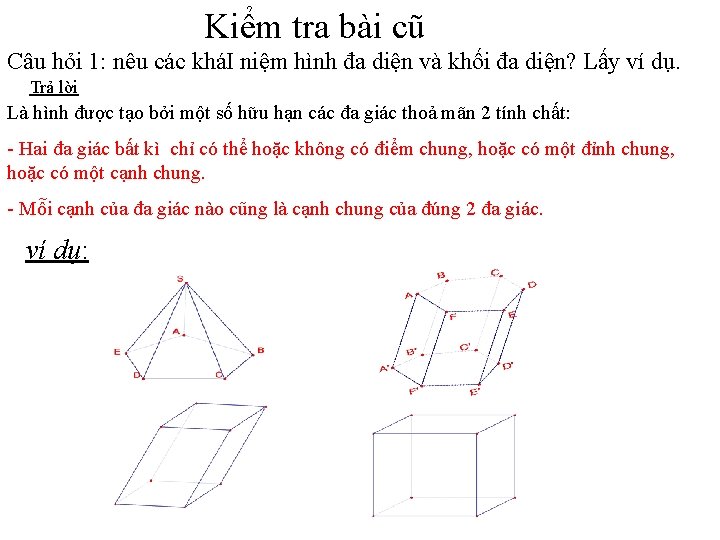
Kiểm tra bài cũ Câu hỏi 1: nêu các kháI niệm hình đa diện và khối đa diện? Lấy ví dụ. Trả lời Là hình được tạo bởi một số hữu hạn các đa giác thoả mãn 2 tính chất: - Hai đa giác bất kì chỉ có thể hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung. - Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 2 đa giác. ví dụ:

BÀI 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU I. Khối đa diện lồi. Định nghĩa: Khối đa diện (H) được gọi là khối đa diện lồi nếu đoan thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Ví dụ: Khối lăng trụ, khối chóp, khối hộp, khối lập phương … là những khối đa diện lồi.

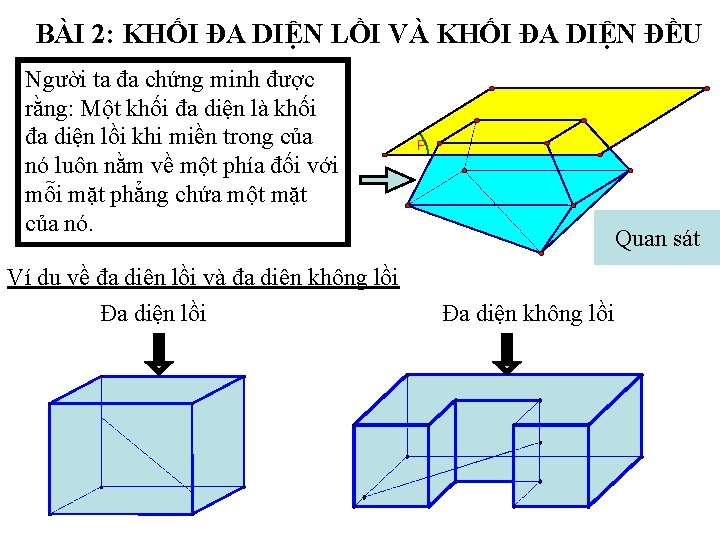
BÀI 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU Người ta đa chứng minh được rằng: Một khối đa diện là khối đa diện lồi khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó. Ví dụ về đa diện lồi và đa diện không lồi Đa diện lồi P Quan sát Đa diện không lồi

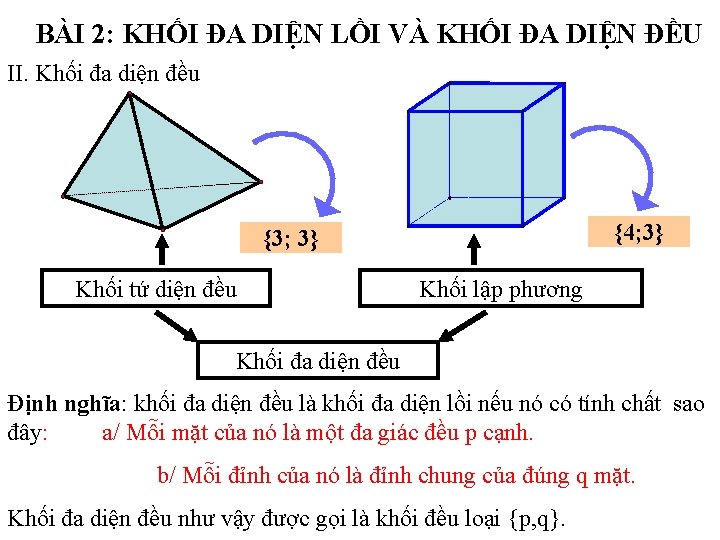
BÀI 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU II. Khối đa diện đều {4; 3} {3; 3} Khối tứ diện đều Khối lập phương Khối đa diện đều Định nghĩa: khối đa diện đều là khối đa diện lồi nếu nó có tính chất sao đây: a/ Mỗi mặt của nó là một đa giác đều p cạnh. b/ Mỗi đỉnh của nó là đỉnh chung của đúng q mặt. Khối đa diện đều như vậy được gọi là khối đều loại {p, q}.

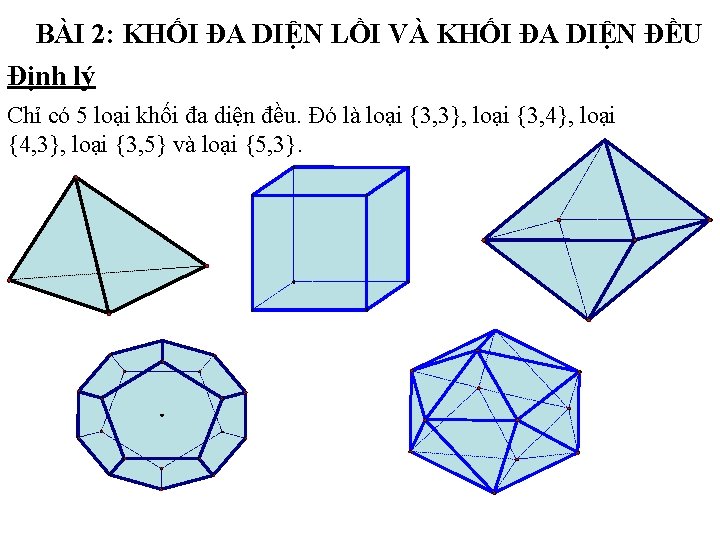
BÀI 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU Định lý Chỉ có 5 loại khối đa diện đều. Đó là loại {3, 3}, loại {3, 4}, loại {4, 3}, loại {3, 5} và loại {5, 3}.

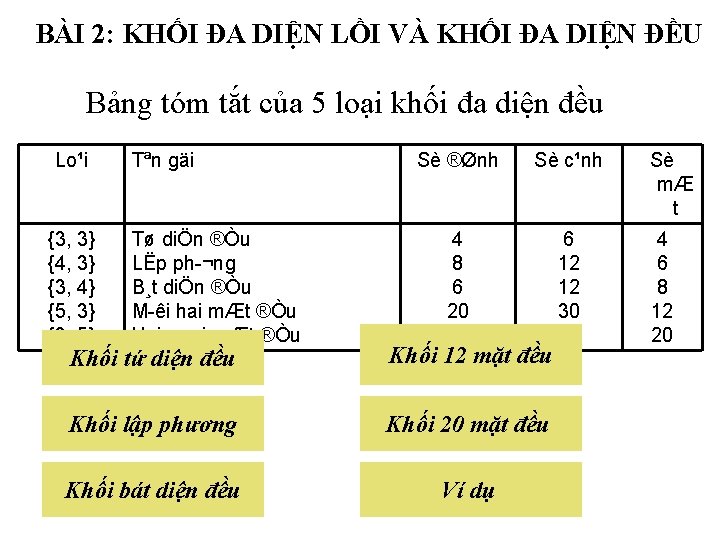
BÀI 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU Bảng tóm tắt của 5 loại khối đa diện đều Lo¹i {3, 3} {4, 3} {3, 4} {5, 3} {3, 5} Tªn gäi Tø diÖn ®Òu LËp ph ¬ng B¸t diÖn ®Òu M êi hai mÆt ®Òu Hai m ¬i mÆt ®Òu Sè ®Ønh Sè c¹nh 4 8 6 20 12 6 12 12 30 30 Khối tứ diện đều Khối 12 mặt đều Khối lập phương Khối 20 mặt đều Khối bát diện đều Ví dụ Sè mÆ t 4 6 8 12 20

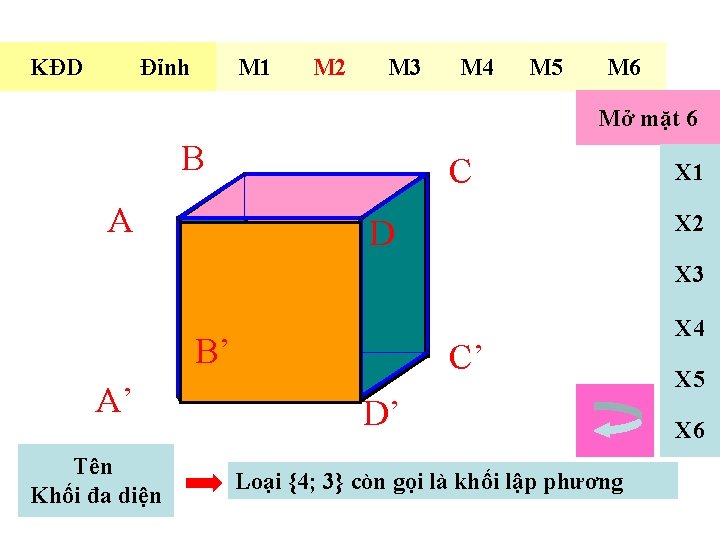
KĐD Đỉnh M 1 M 2 M 3 M 4 M 5 M 6 Mở mặt 6 B A C X 1 X 2 D X 3 B’ A’ Tên Khối đa diện C’ D’ Loại {4; 3} còn gọi là khối lập phương X 4 X 5 X 6

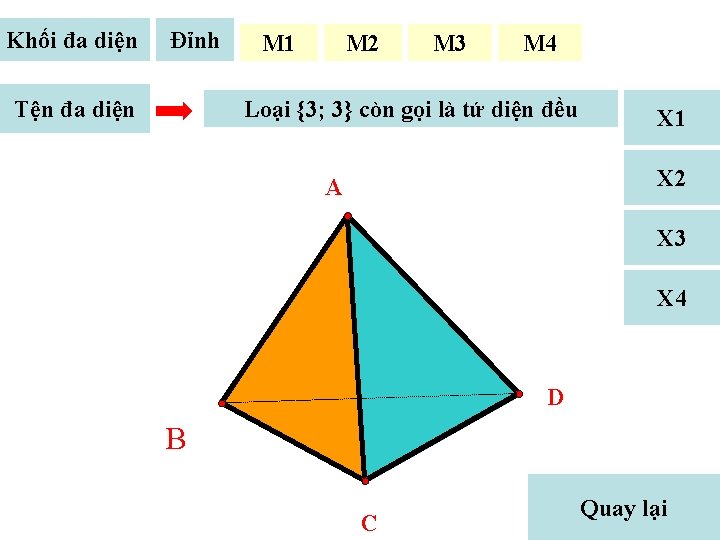
Khối đa diện Đỉnh Tện đa diện M 1 M 2 M 3 M 4 Loại {3; 3} còn gọi là tứ diện đều X 1 X 2 A X 3 X 4 D B C Quay lại

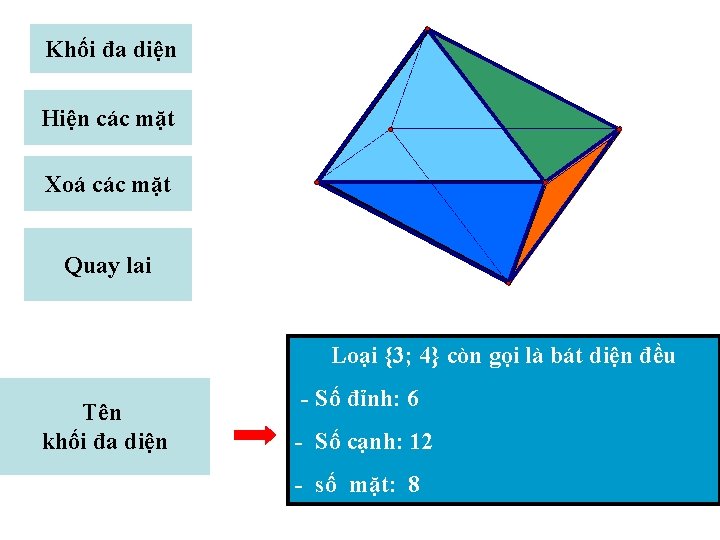
Khối đa diện Hiện các mặt Xoá các mặt Quay lai Loại {3; 4} còn gọi là bát diện đều Tên khối đa diện - Số đỉnh: 6 - Số cạnh: 12 - số mặt: 8

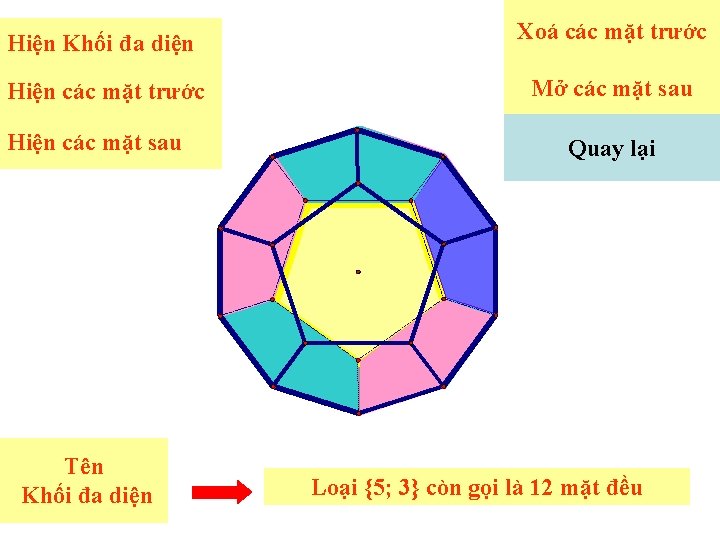
Hiện Khối đa diện Xoá các mặt trước Hiện các mặt trước Mở các mặt sau Hiện các mặt sau Tên Khối đa diện Quay lại Loại {5; 3} còn gọi là 12 mặt đều

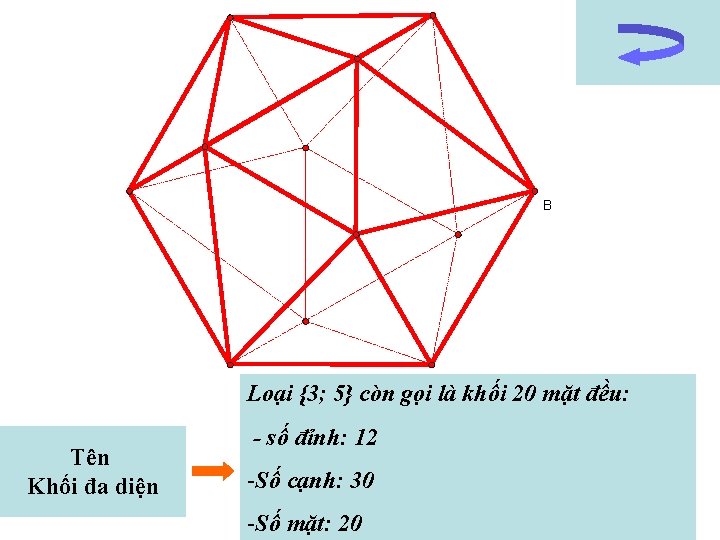
B Loại {3; 5} còn gọi là khối 20 mặt đều: Tên Khối đa diện - số đỉnh: 12 -Số cạnh: 30 -Số mặt: 20

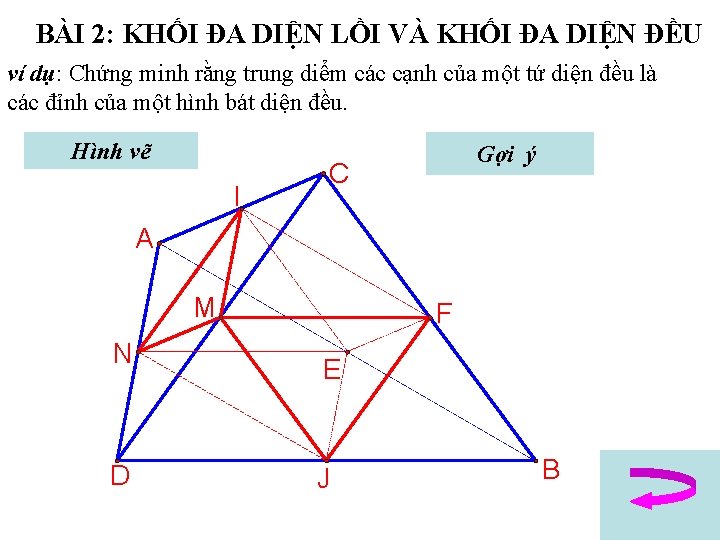
BÀI 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU ví dụ: Chứng minh rằng trung diểm các cạnh của một tứ diện đều là các đỉnh của một hình bát diện đều. Hình vẽ Hide Segments I Gợi ý C A M N D F E J B