bi c 1 Gi d l t y2

bµi cò : 1. Gọi (d) là đt y=2 x và (d’) là đt y =2 x-3. Ta có thể coi (d’) là do tịnh tiến (d): a) Lên trên hay xuống dưới bao nhiêu đơn vị ? d Đặt f(x) = 2 x => 2 x-3 = f(x) - 3=>(d’) là do (d) tịnh tiến xuống dưới 3 đơn vị. d' o b) Sang phải hay sang trái bao nhiêu đơn vị ? Viết 2 x-3 = 2(x-1, 5) = f(x-1, 5)=>(d’) là (d) tịnh tiến sang phải 1, 5 đơn vị. 1, 5 -3

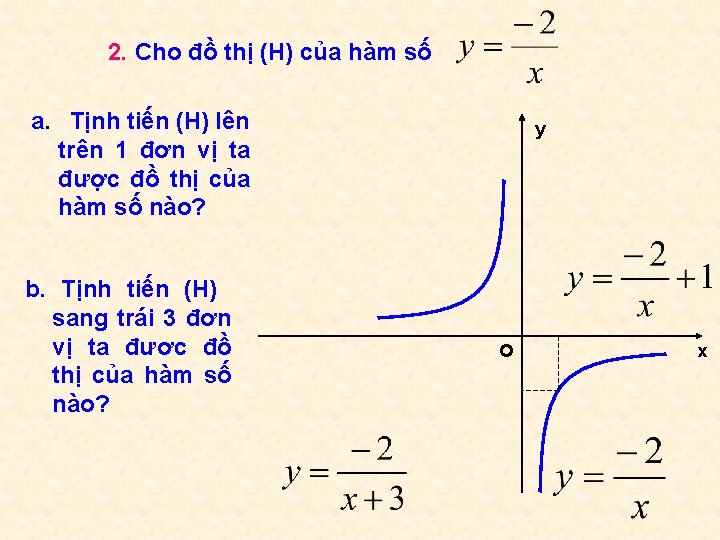
2. Cho đồ thị (H) của hàm số a. Tịnh tiến (H) lên trên 1 đơn vị ta được đồ thị của hàm số nào? b. Tịnh tiến (H) sang trái 3 đơn vị ta đươc đồ thị của hàm số nào? y o x

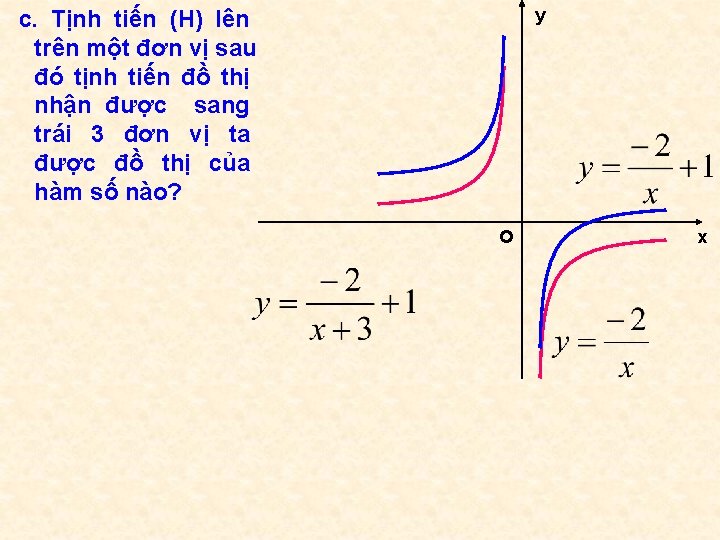
y c. Tịnh tiến (H) lên trên một đơn vị sau đó tịnh tiến đồ thị nhận được sang trái 3 đơn vị ta được đồ thị của hàm số nào? o x

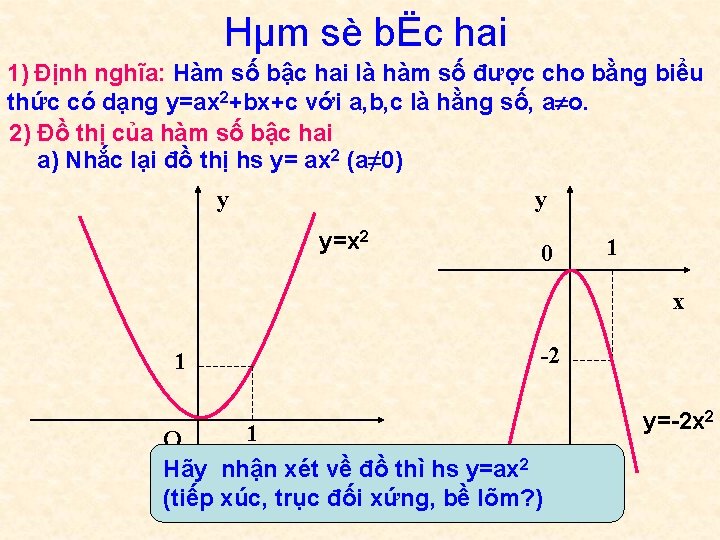
Hµm sè bËc hai 1) Định nghĩa: Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y=ax 2+bx+c với a, b, c là hằng số, a o. 2) Đồ thị của hàm số bậc hai a) Nhắc lại đồ thị hs y= ax 2 (a≠ 0) y y y=x 2 0 1 x 1 -2 1 O x Hãy nhận xét về đồ thì hs y=ax 2 (tiếp xúc, trục đối xứng, bề lõm? ) y=-2 x 2

Đồ thị hs y=ax 2 là một Parabol: • • Tiếp xúc với trục hoành tại gốc tọa độ. Nhận trục tung làm trục đối xứng. Quay bề lõm lên trên nếu a>0. Quay bề lõm xuống dưới nếu a<0.

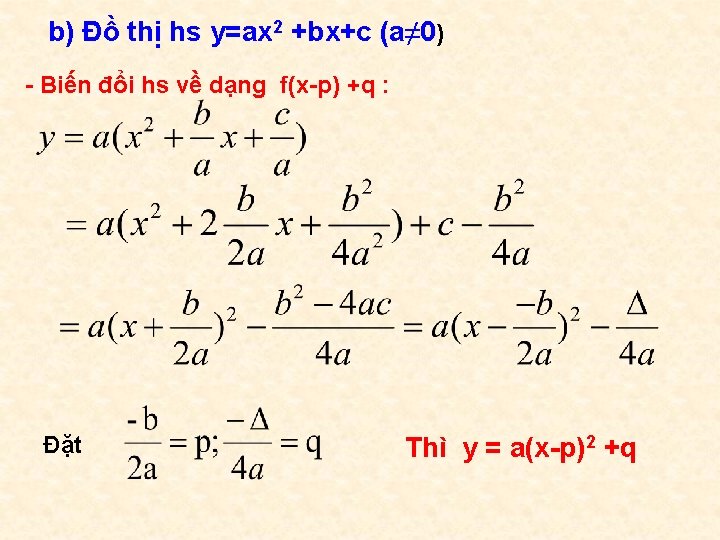
b) Đồ thị hs y=ax 2 +bx+c (a≠ 0) - Biến đổi hs về dạng f(x-p) +q : Đặt Thì y = a(x-p)2 +q

-Vẽ đå thÞ hµm sè y=ax 2+bx+c (a o) Gọi (P 0) là Parbol y =ax 2 1/ Tịnh tiến (P 0) sang phải p đơn vị (p>o) ta được đồ thị hs y = a(x-p)2 (P 1) (P) y (P 0) (P 1) 2/ Tịnh tiến (P 1) lên trên q đơn vị (q>o) ta được đồ thị hs y = a(x-p)2+q (P) q p x

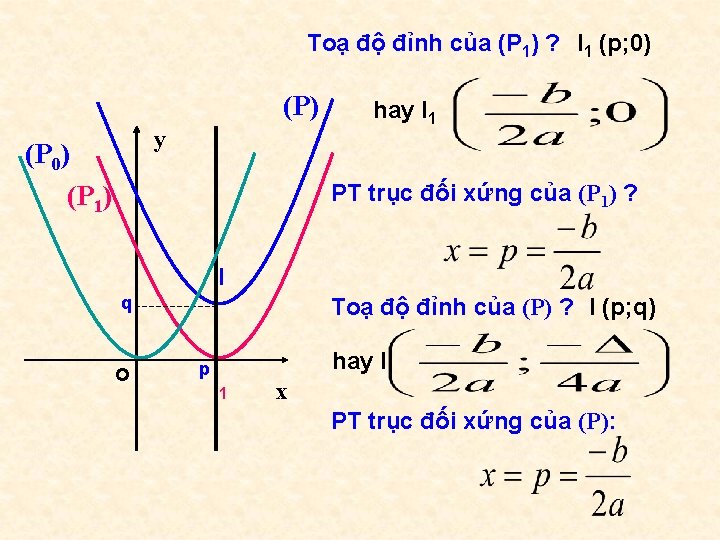
Toạ độ đỉnh của (P 1) ? I 1 (p; 0) (P) y (P 0) (P 1) hay I 1 PT trục đối xứng của (P 1) ? I q o Toạ độ đỉnh của (P) ? I (p; q) p I 1 hay I x PT trục đối xứng của (P):

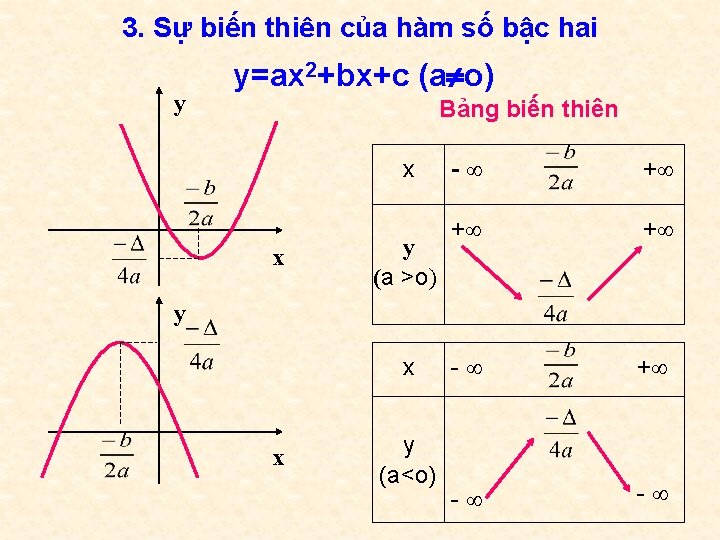
3. Sự biến thiên của hàm số bậc hai y y=ax 2+bx+c (a o) Bảng biến thiên x x y (a >o) - + + + - - y x x y (a<o)

Cổng Ac-xơ

ĐẠI HỌC BÁCH KHOA HÀ NỘI

Cầu treo Cổng vàng

Đèn fa

Cách vẽ Parabol • 1. Tính toạ độ đỉnh: I • 2. Lập bảng biến thiên (Xác định trục đối xứng và hướng bề lõm của Parabol) • 3. Xác định một số điểm thuộc Parabol (giao điểm của Parabol với các trục toạ độ và các điểm đối xứng của chúng qua trục đối xứng). • 4. Dựa vào bảng biến thiên để nối các điểm vừa xác định với nhau.

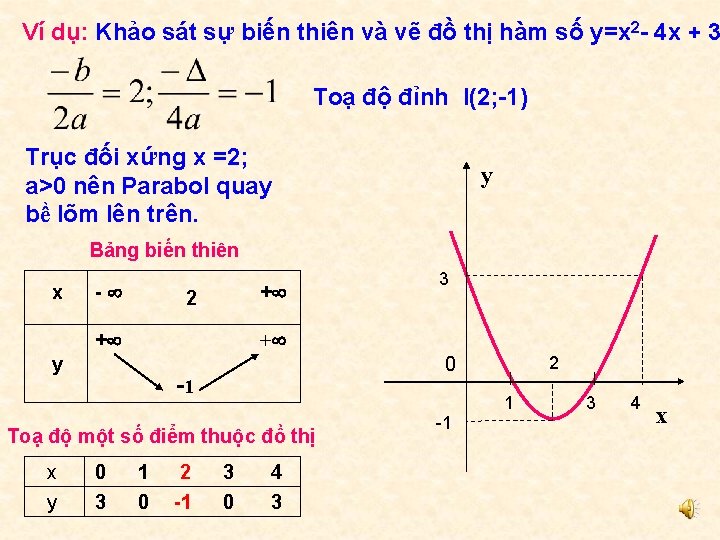
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị hàm số y=x 2 - 4 x + 3 Toạ độ đỉnh I(2; -1) Trục đối xứng x =2; a>0 nên Parabol quay bề lõm lên trên. y Bảng biến thiên x - + 2 + + y 0 -1 Toạ độ một số điểm thuộc đồ thị x y 0 3 3 1 0 2 -1 3 0 4 3 -1 2 1 3 4 x

Ứng dụng: Dựa vào đồ thị sau để giải bài toán: a. Với giá trị nào của x thì : + y > o ? y < o ? + y đạt giá trị nhỏ nhất ? Tính giá trị đó. b. Biện luận theo m số nghiệm của pt: x 2 - 4 x + 3 = m (*) Bài giải y 3 0 -1 m m 1 m 2 3 4 x a. y > o khi x < 1 hoặc x > 3 y < o khi 1< x < 3 GTNH của y bằng -1 khi x = 2 b. Số nghiệm của pt (*) là số giao điểm của Parabol y =x 2 - 4 x+3 (P) với đường thẳng y = m (d) ü m < -1: (d) (P) = pt vô nghiệm ü m = -1: (d) tiếp xúc (P) pt có nghiệm kép. ü m >-1: (d) (P) = 2 điểm pt có hai nghiệm phân biệt

BTVN: 27; 28; 29; 30