BI 1 KHI NIM V KHI A DIN


BÀI 1 KHÁI NIỆM VỀ KHỐI ĐA DIỆN

Câu 1: Định nghĩa nào đúng về hình lăng trụ? A) Hình lăng trụ là hình có hai đáy là 2 đa giác bằng nhau và các mặt bên là các hình bình hành. B) Hình lăng trụ là hình có hai đáy là 2 đa giác song và bằng nhau và các mặt bên là các hình bình hành. C) Hình lăng trụ là hình có hai đáy là 2 đa giác song và bằng nhau và các mặt bên là các hình chữ nhật. D) Hình lăng trụ là hình có hai đáy là 2 đa giác song và các mặt bên là các hình chữ nhật. Đúng rồi Click để tiếp tục Sai rồi Click để tiếp tục Bạn phải trả lời câu hỏi này trước khi tiếp tục Chấp nhận Xóa

Câu 2: Định nghĩa nào đúng về hình chóp? A) Hình chóp là hình có đáy là đa giác và các mặt bên là tam giác chung đỉnh B) Hình chóp là hình có đáy là tam giác và các mặt bên là đa giác chung đỉnh C) Hình chóp là hình có đáy là tứ giác và các mặt bên là tam giác chung đỉnh D) Hình chóp là hình có đáy là đa giác và các mặt bên là đa giác chung đỉnh Đúng rồi Click để tiếp tục Sai rồi Click để tiếp tục Bạn phải trả lời câu hỏi này trước khi tiếp tục Chấp nhận Xóa

I. Khối lăng trụ và khối chóp * Nhắc lại định nghĩa hình lăng trụ và hình chóp : + Hình lăng trụ là hình có hai đáy là hai đa giác song và bằng nhau và các mặt bên là các hình bình hành. + Hình chóp là hình có đáy là đa giác và các mặt bên là tam giác chung đỉnh.

+ Quan sát khối Rubic : Nhận thấy : * Các mặt ngoài của nó tạo thành hình lập phương * Ta nói rằng khối rubic là một khối lập phương
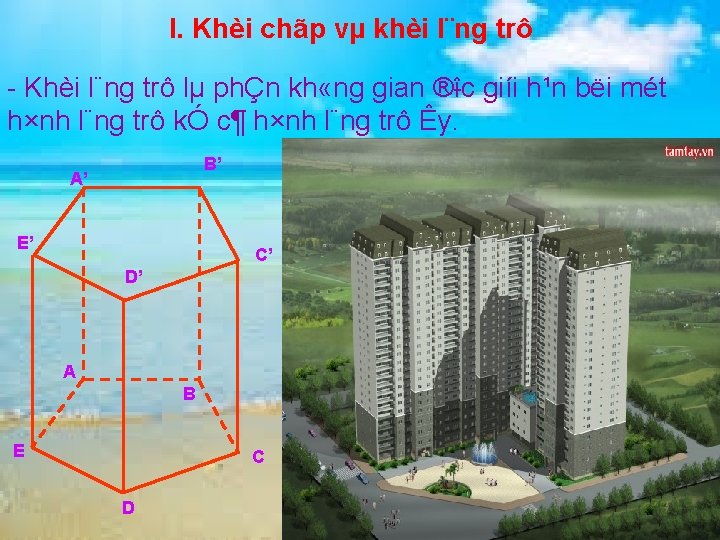
I. Khèi chãp vµ khèi l¨ng trô Khèi l¨ng trô lµ phÇn kh «ng gian ® îc giíi h¹n bëi mét h×nh l¨ng trô kÓ c¶ h×nh l¨ng trô Êy. B’ A’ E’ C’ D’ A B E C D

Khèi chãp lµ phÇn kh «ng gian ® îc giíi h¹n bëi mét h×nh chãp kÓ c¶ h×nh chãp Êy.
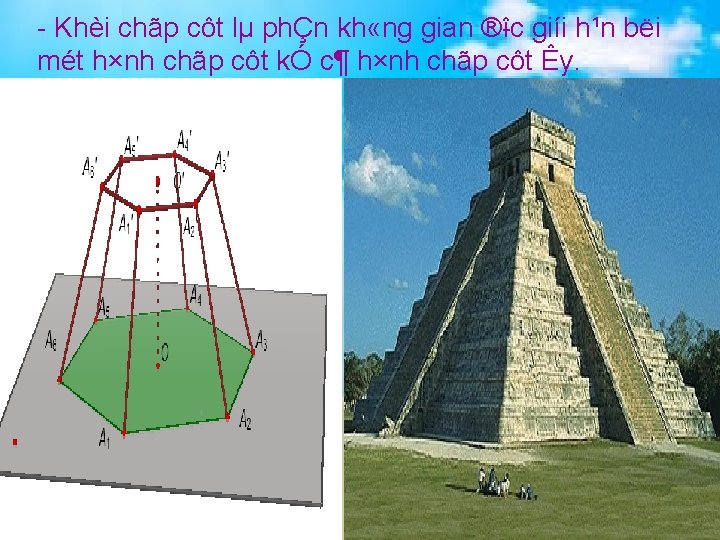
Khèi chãp côt lµ phÇn kh «ng gian ® îc giíi h¹n bëi mét h×nh chãp côt kÓ c¶ h×nh chãp côt Êy.

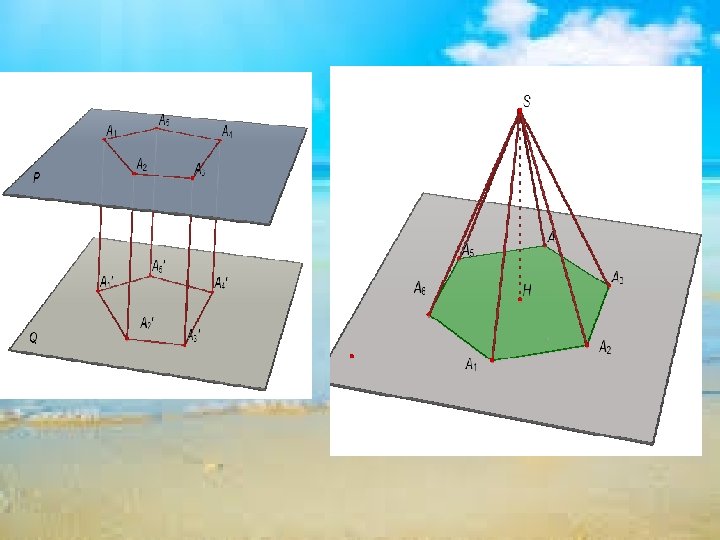
* Tªn cña khèi l¨ng trô hay khèi chãp ® îc ®Æt theo tªn cña h×nh l¨ng trô hay h×nh chãp giíi h¹n nã. * C¸c ®Ønh, c¹nh, mÆt bªn, mÆt ®¸y, c¹nh bªn, c¹nh ®¸y… cña mét h×nh l¨ng trô (h×nh chãp hay h×nh chãp côt) theo thø tù lµ ®Ønh, c¹nh, mÆt bªn, mÆt ®¸y, c¹nh bªn, c¹nh ®¸y… cña khèi l¨ng trô (khèi chãp hay khèi chãp côt) t ¬ngøng. * §iÓm kh «ng thuéc khèi l¨ng trô ® îc gäi lµ ®iÓm ngoµi cña l¨ng trô, ®iÓm thuéc khèi l¨ng trô nh ng kh «ng thuéc h×nh l¨ng trô øng víi khèi l¨ng trô ®ã ® îc gäi lµ ®iÓm trong cña khèi l¨ng trô.
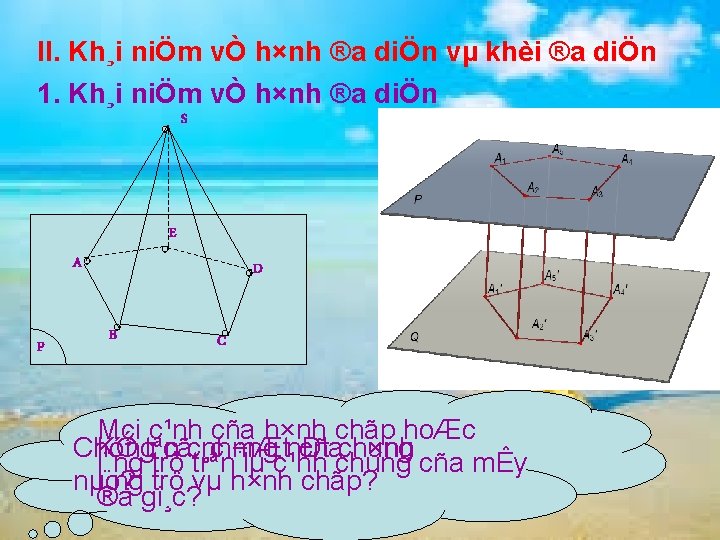
II. Kh¸i niÖm vÒ h×nh ®a diÖn vµ khèi ®a diÖn 1. Kh¸i niÖm vÒ h×nh ®a diÖn S E A P D B C Mçi c¹nh cña h×nh chãp hoÆc Chóng KÓ tªn cãc¸c nh÷ng mÆtnÐt cñachung h×nh l¨ng trô trªn lµ c¹nh chung cña mÊy nµo? l¨ng trô vµ h×nh chãp? ®a gi¸c?

Khái niệm về hình đa diện - Các hình trên đều có chung là những hình không gian được tạo bởi một số hữu hạn đa giác, trong ®ã : + Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung nào hoặc chỉ có một điểm chung hoặc chỉ có một cạnh chung +Mỗi cạnh của đa giác nào cũng là cạnh chung của hai đa giác Hình đa diện (đa diện) là hình được tạo bởi hữu hạn đa giác thoả mãn hai tính chất trên

2. Khái niệm về khối đa diện Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện ®ã.
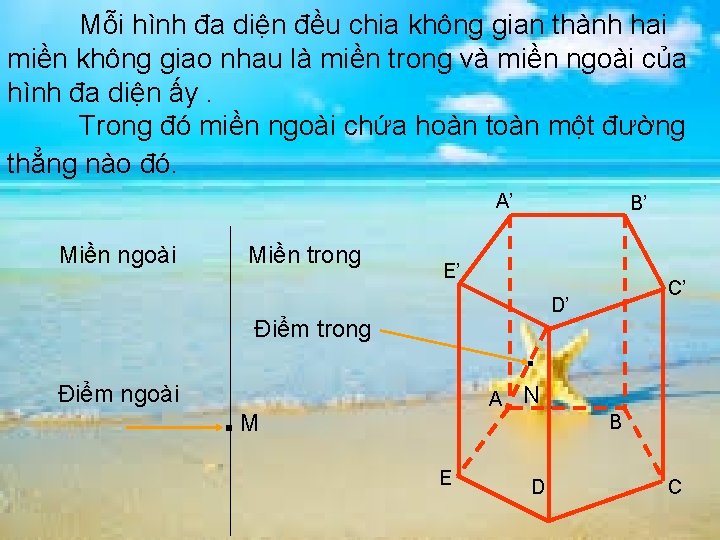
Mỗi hình đa diện đều chia không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện ấy. Trong đó miền ngoài chứa hoàn toàn một đường thẳng nào đó. A’ Miền ngoài Miền trong E’ . Điểm trong Điểm ngoài . B’ A M C’ D’ N B E D C

Hỏi : Các hình sau đây hình nào là khối đa diện, hình nào không phải?
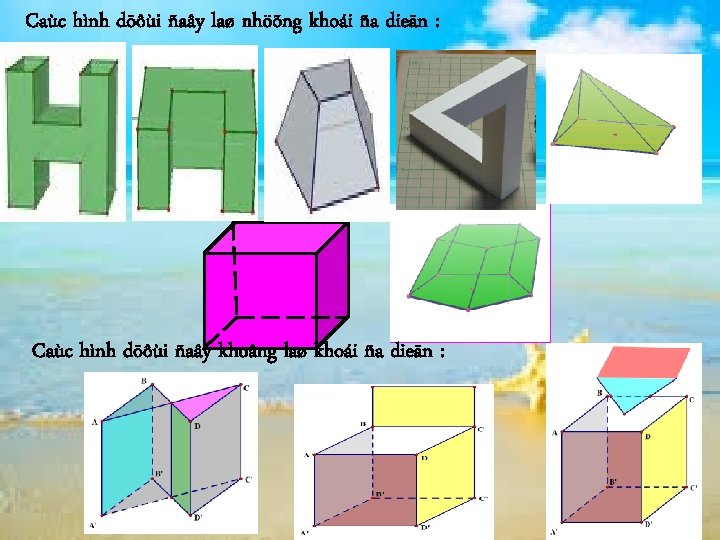
Caùc hình döôùi ñaây laø nhöõng khoái ña dieän : Caùc hình döôùi ñaây khoâng laø khoái ña dieän :

III. Hai đa diện bằng nhau 1. Phép dời hình trong không gian được định nghĩa như trong mặt phẳng. Trong không gian , quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất được gọi là phép biến hình trong không gian. Phép biến hình trong không gian được gọi là phép dời hình trong không gian nếu nó bảo toàn khoảng cách giữa hai điểm tuỳ ý.

Ví dụ : a. Phép tịnh tiến theo véctơ v: là phép biến hình biến mỗi điểm M thành điểm M’ sao cho : M’ V M

b. Phép đối xứng qua mặt phẳng (P): là phép biến hình biến M thành M’ sao cho : + Nếu M thuộc (P) thì M’ trùng với M +Nếu M không thuộc (P) thì MM’ nhận (P) là mặt phẳng trung trực Nếu qua mp(P) hình (H) biến thành chính nó thì (P) gọi là mp đối xứng của hình (H)) M I P M’

c. Phép đối xứng tâm O : là phép biến hình biến M thành M’ sao cho : + Điểm O biến thành chính nó + Nếu M khác O thì MM’ nhận O là trung điểm ( O : gọi là tâm đối xứng ) M’ . O M

d. Phép đối xứng qua đường thẳng (d) : là phép biến hình biến mọi điểm trên (d) thành chính nó, biến mỗi điểm M không thuộc (d) thành M’ sao cho : (d) là đường thẳng trung trực của MM’ Nếu qua (d) hình (H) biến thành chính nó thì (d) gọi là trục đối xứng của hình (H) d M’ M

Nhận xét : + Thực hiện liên tiếp các phép dời hình được một phép dời hình + Phép dời hình biến đa diện (H) thành đa diện (H’) : thì đỉnh, cạnh, mặt của (H) thành đỉnh, cạnh, mặt tương ứng của (H’) 2. Hai hình bằng nhau : Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình nọ thành hình kia

Đặc biệt : Hai hình đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình đa diện nọ thành hình đa diện kia

Ví dụ : Xét phép tịnh tiến theo v biến (H) thành (H’) sau đó thực hiện phép đối xứng tâm (O) hình (H’) biến thành hình (H’’). Do đó có một phép dời hình biến (H) thành (H’’) Tức là hai hình (H) và (H’’) bằng nhau. (H’) v O (H”) (H)

IV. Phân chia và lắp ghép các khối đa diện Nếu khối đa diện (H) là hợp của 2 khối đa diện (H’) và (H’’) sao cho (H’) và (H’’) không có điểm chung điểm trong nào thì có thể chia khối đa diện (H) thành 2 khối đa diện (H’) và (H’’) , hay có thể lắp ghép hai khối đa diện (H’) và (H’’) với nhau để được khối đa diện (H)
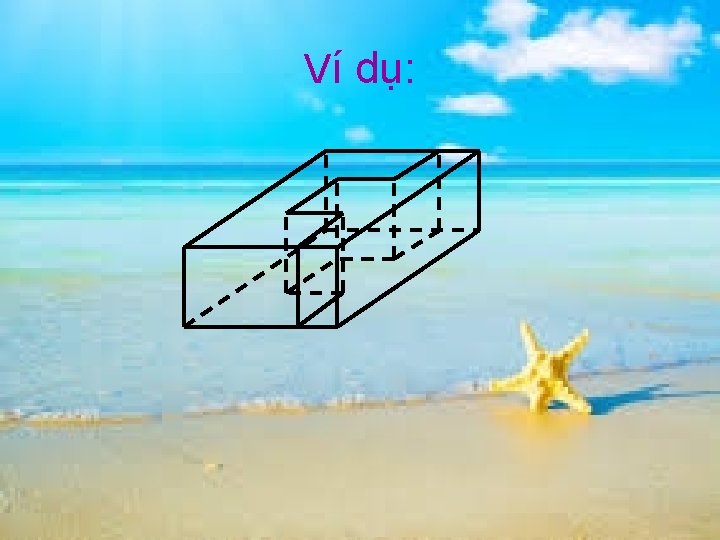
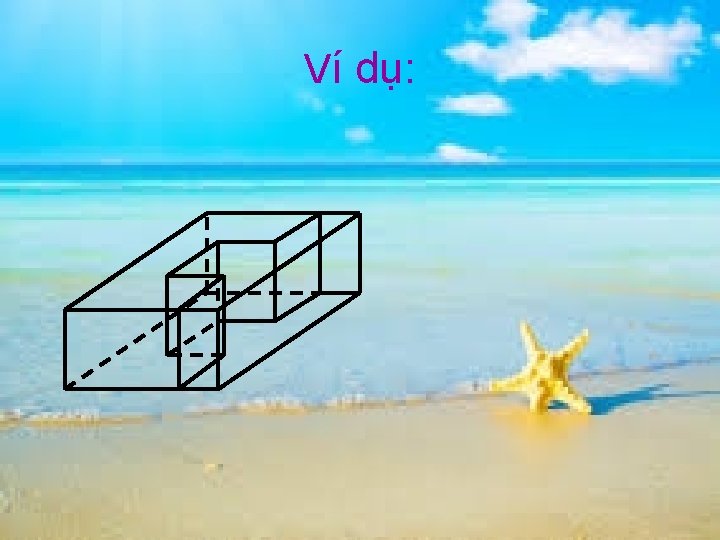
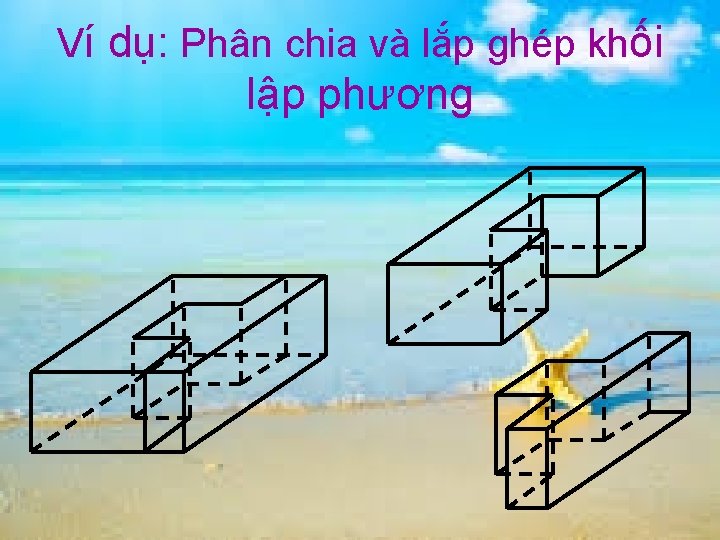
Ví dụ: Phân chia và lắp ghép khối lập phương
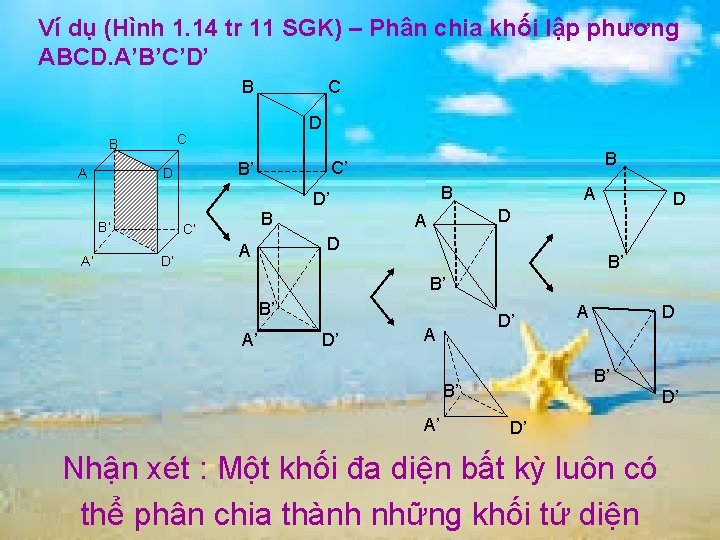
Ví dụ (Hình 1. 14 tr 11 SGK) – Phân chia khối lập phương ABCD. A’B’C’D’ B B C’ D’ B C’ B’ D B’ A’ D C B A C B D’ A D A D B’ B’ B’ A’ D’ D’ A D B’ B’ A’ A D’ D’ Nhận xét : Một khối đa diện bất kỳ luôn có thể phân chia thành những khối tứ diện

Củng cố : • • • Khối chóp , khối lăng trụ. Khối đa diện Hai đa diện bằng nhau Phân chia và lắp ghép khối đa diện Bài tập : Bài 1, bài 2, bài 3, bài 4 (Tr 12) Các em về nhà đọc bài đọc thêm (Tr 12)

Câu 1: Thế nào là khối đa diện? A) Khối đa diện là phần không gian được giới hạn bởi hình chóp, kể cả hình chóp đó B) Khối đa diện là phần không gian được giới hạn bởi hình lăng trụ, kể cả hình lăng trụ đó C) Khối đa diện là tập hợp tất cả các điểm nằm trong hình đa diện D) Khối đa diện là phần không gian được giới hạn bởi hình đa diện, kể cả hình đa diện đó Đúng rồi Click để tiếp tục Sai rồi Click để tiếp tục Bạn phải trả lời câu hỏi này trước khi tiếp tục Chấp nhận Xóa

Câu 2: Cho hình hộp ABCD. A'B'C'D'. Hai lăng trụ ABD. A'B'D' và BCD. B'C'D' bằng nhau, vì sao? A) Có phép đối xứng trục B'D biến lăng trụ ABD. A'B'D' thành lăng trụ BCD. B'C'D' B) Có phép đối xứng tâm O của hình hộp biến lăng trụ ABD. A'B'D' thành lăng trụ BCD. B'C'D' C) Có phép đối xứng trục BD' biến lăng trụ ABD. A'B'D' thành lăng trụ BCD. B'C'D' D) Đáp án khác Đúng rồi Click để tiếp tục Sai rồi Click để tiếp tục Bạn phải trả lời câu hỏi này trước khi tiếp tục Chấp nhận Xóa

Bài học của chúng ta đến đây là kết thúc ! Chúc các thầy, cô và các em mạnh khoẻ, hạnh phúc và thành đạt.
- Slides: 34