BFS and DFS BFS BFS takes a graph

BFS and DFS

BFS • BFS takes a graph given as an adjacency list. • Starting from a specified source vertex s to V , BFS visits every vertex v to V that can be reached from s, and keeps track of the path from s to v with the smallest number of edges. • BFS works on directed or undirected graphs: we describe it for directed graphs.

Procedure-BFS • We start at vertex ‘v’ and make it as visited • All unvisited vertices adjacent to ‘v’ are visited next • Then unvisited vertices adjacent to these vertices are visited next • This process will continue untill all vertices have been visited

Pseudo code Algorithm BFS(v) { Visited v=true; Initialize queue to 0; addqueue (q, v); While not empty queue(q) { deletequeue(q, v); For all vertices ‘w’ adjacent to ‘v’ If(visited(w)!=true) then addqueue(q, w); Visited(w)=true; }

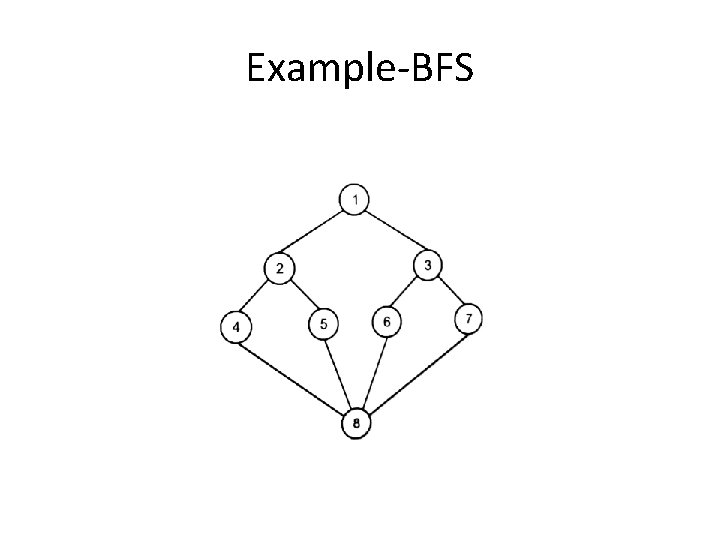
Example-BFS

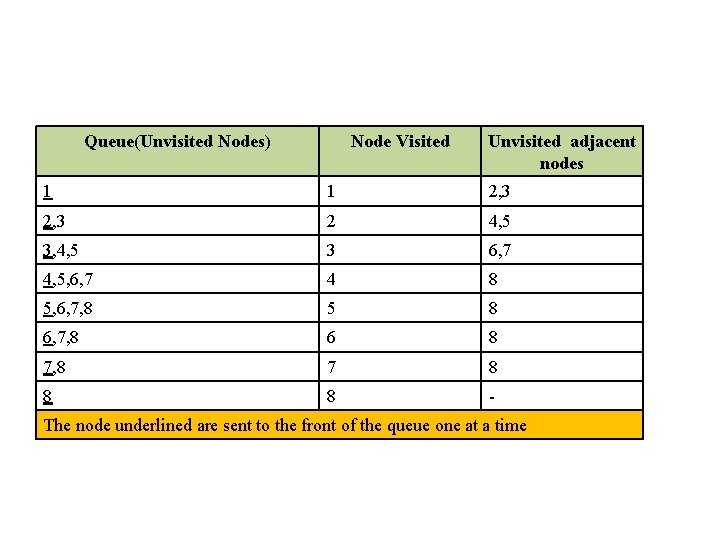
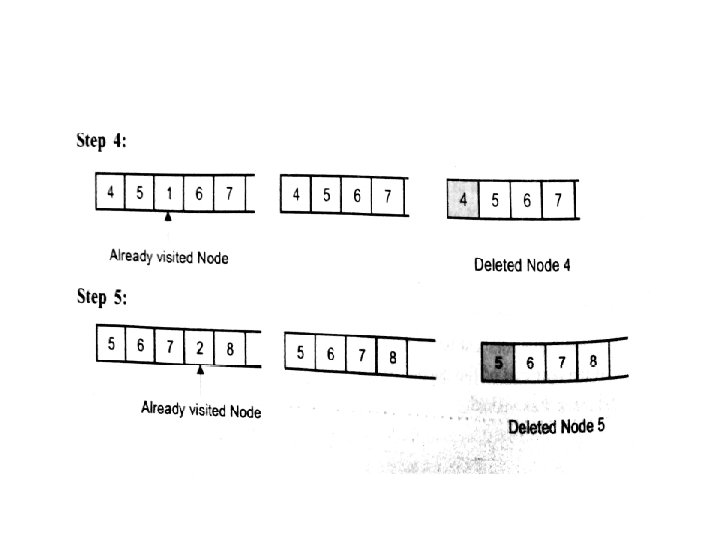
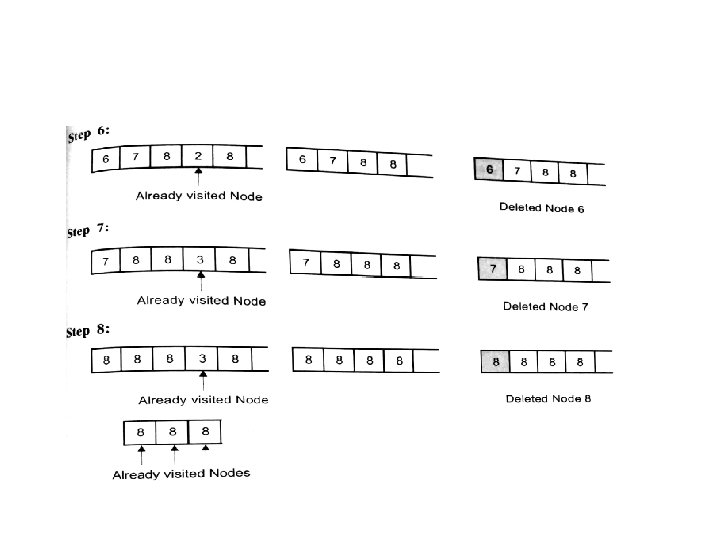
Queue(Unvisited Nodes) Node Visited Unvisited adjacent nodes 1 1 2, 3 2 4, 5 3, 4, 5 3 6, 7 4, 5, 6, 7 4 8 5, 6, 7, 8 5 8 6, 7, 8 6 8 7, 8 7 8 8 8 - The node underlined are sent to the front of the queue one at a time

Diagrammatic Representation

DFS • DFS starts by selecting one vertex V of G as a start vertex; V is marked visited. • Then each unvisited vertex adjacent to V is searched in turn using depth first search recursively. • This process continues until a dead end (i. e)a vertex with no adjacent unvisited vertices is encountered. • At a dead end, the algorithm backup one edge to the vertex it came from and tries to continue visiting unvisited vertices from there.

Procedure-BFS • We start at vertex ‘v’ and make it as visited • All unvisited vertices ‘w’ adjacent to ‘v’ is selected • Call the same algorithm with vertex ‘w’ • This process will continue untill all vertices have been visited

Procedure-DFS • Choose any node in the graph. Designate it as the search node and mark it as visited • Using adjacency matrix of the graph, find a node adjacent to the search node that has not been visited yet. Designate this as the new search node and mark it as visited • Repeat step 2 using the new search node. If no nodes satisfying (2) can be found to the previous search node and continue from there • When a return to the previous search node in (3) is impossible, the search from the originally chosen search node is complete • If the graph still contains unvisited nodes choose any node that has not been visited &repeat step(1) through (4)

Pseudo code Algorithm DFS(Vertex V) { Visited[v]=True; For each W adjacent to V If(!unvisited[W]) DFS(W); }

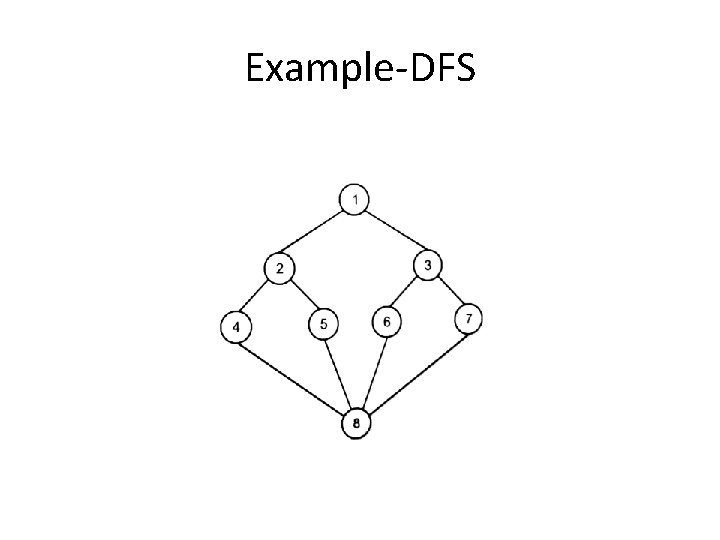
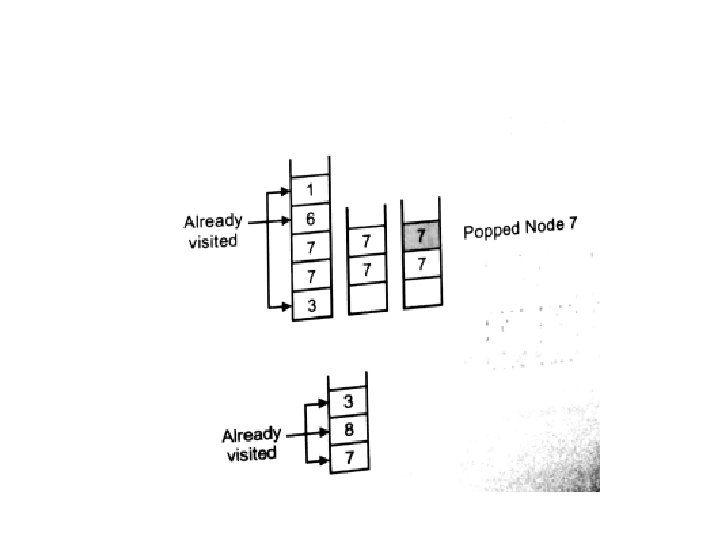
Example-DFS

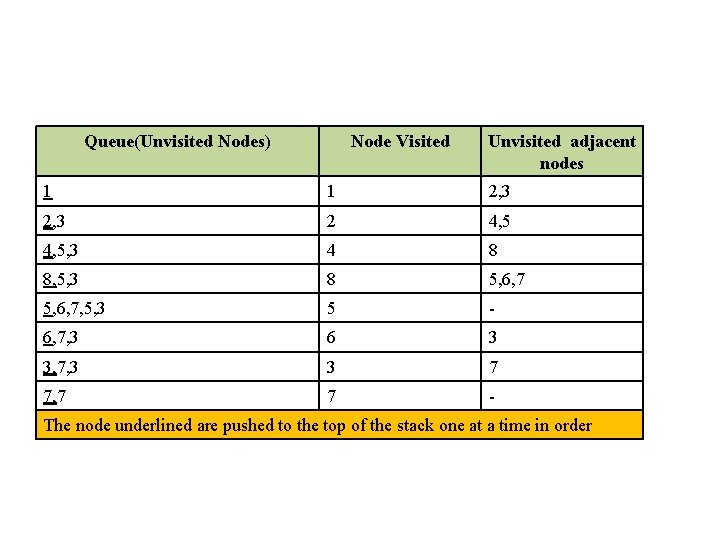
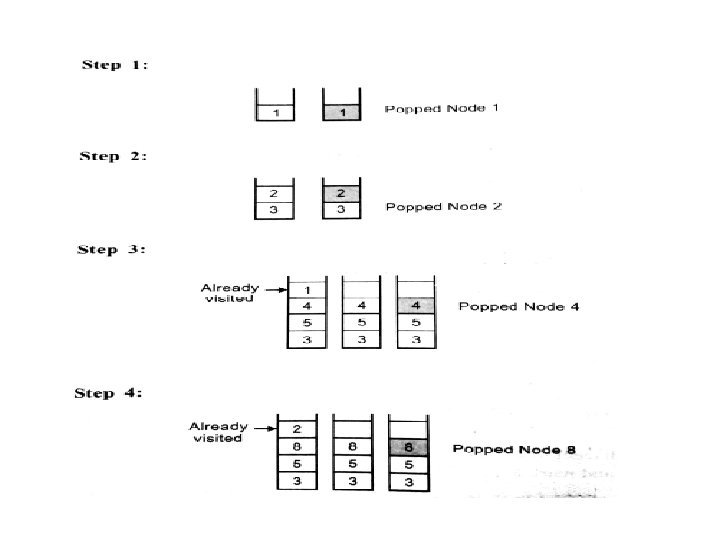
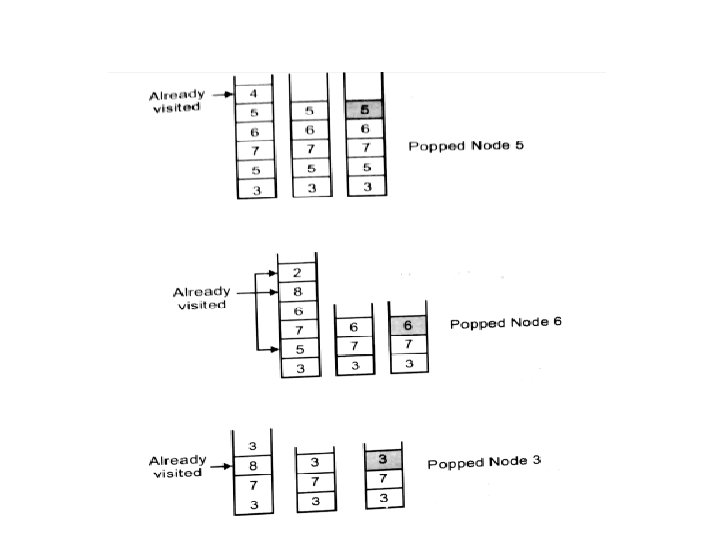
Queue(Unvisited Nodes) Node Visited Unvisited adjacent nodes 1 1 2, 3 2 4, 5, 3 4 8 8, 5, 3 8 5, 6, 7, 5, 3 5 - 6, 7, 3 6 3 3, 7, 3 3 7 7, 7 7 - The node underlined are pushed to the top of the stack one at a time in order