Beyond mean field in the particlevibration scheme Marcello

Beyond mean field in the particle-vibration scheme Marcello Baldo INFN – Catania Dedicated to Eduard, beloved friend Dubna 20 -22 March 2019

WHY BEYOND THE MEAN FIELD ? 1. The energy density functional method is extremely successful in reproducing the nuclear bindings. However the single particle energies show clear discrepancy with the phenomenological data. 2. To introduce many-body correlations that cannot be included in the EDF. 3. To describe fragmentation and width of the single particle states and of e. g. Giant Resonances.

HOW BEYOND THE MEAN FIELD ? Since the effective interaction or EDF should include to a large extent the short range correlations that are present in the nuclear system, what is missing is mainly the long-range correlations. They can be introduced in the particle-vibration coupling scheme, where the collective nuclear excitations involve the whole nucleus and are therefore of long-range character. We introduce explicitly the ‘phonons’ degrees of freedom in the many-body scheme, considered still at microscopic level. Particle and phonon degrees of freedom

OUTLOOK Preliminaries on the mean field The TFFS approach Magic nuclei Semi-magic nuclei The functional derivative approach Comparison between the approaches Conclusion

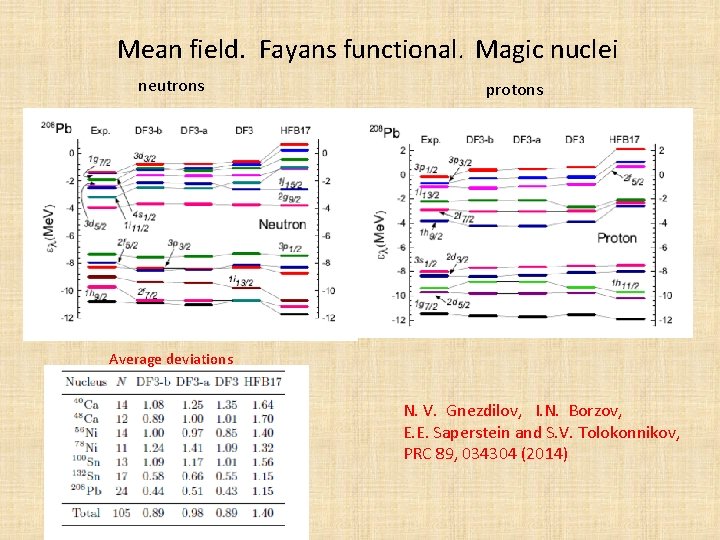
Mean field. Fayans functional. Magic nuclei neutrons protons Average deviations N. V. Gnezdilov, I. N. Borzov, E. E. Saperstein and S. V. Tolokonnikov, PRC 89, 034304 (2014)

Let us consider a generic energy density functional and expand around the minimum in the density matrix Hartree-Fock potential Effective two-body interaction

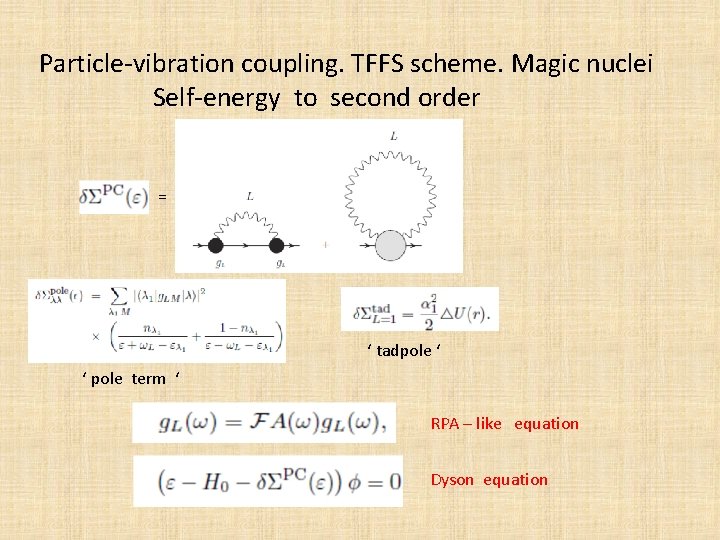
Particle-vibration coupling. TFFS scheme. Magic nuclei Self-energy to second order = ‘ tadpole ‘ ‘ pole term ‘ RPA – like equation Dyson equation

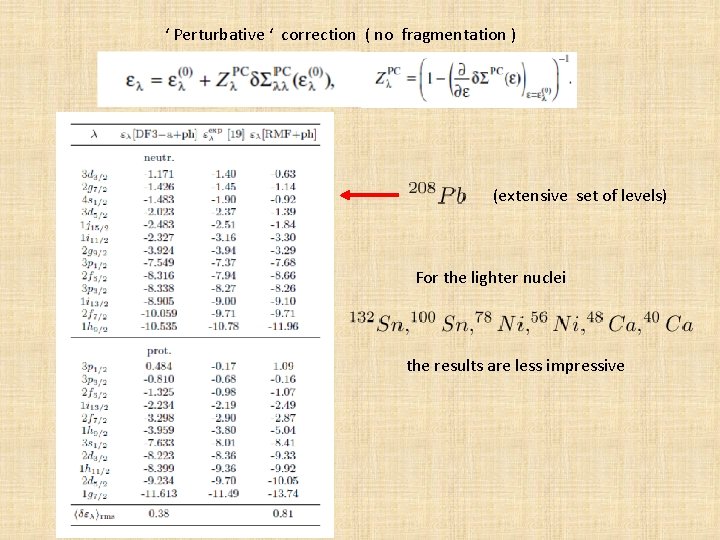
‘ Perturbative ‘ correction ( no fragmentation ) (extensive set of levels) For the lighter nuclei the results are less impressive

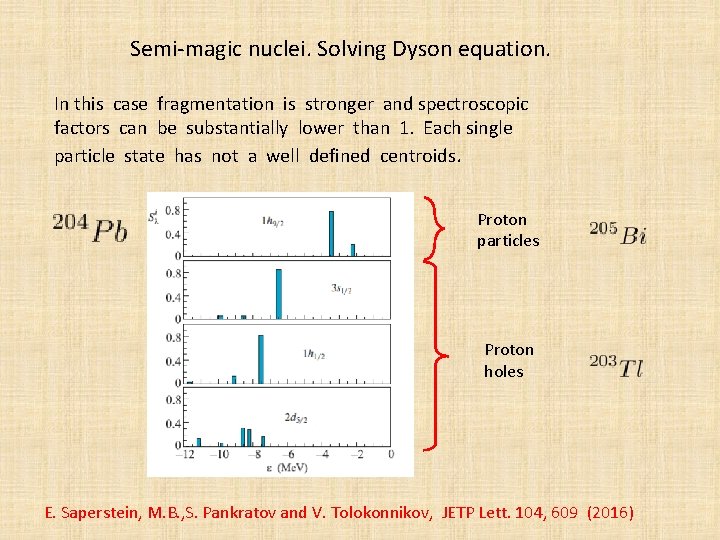
Semi-magic nuclei. Solving Dyson equation. In this case fragmentation is stronger and spectroscopic factors can be substantially lower than 1. Each single particle state has not a well defined centroids. Proton particles Proton holes E. Saperstein, M. B. , S. Pankratov and V. Tolokonnikov, JETP Lett. 104, 609 (2016)

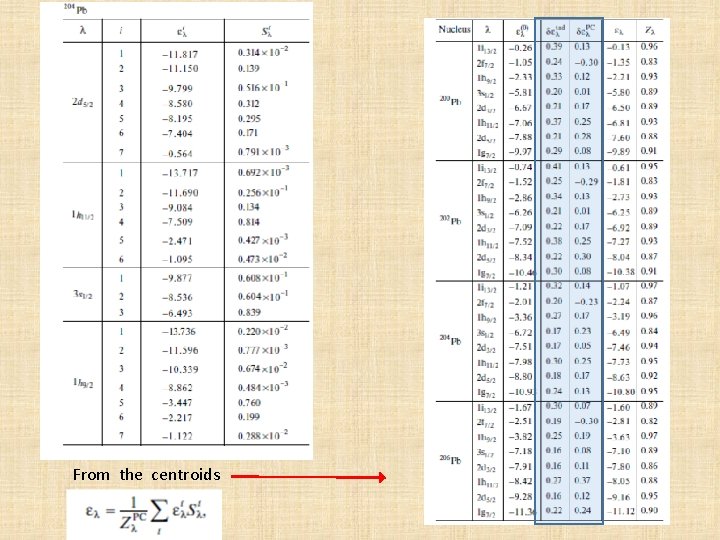
From the centroids

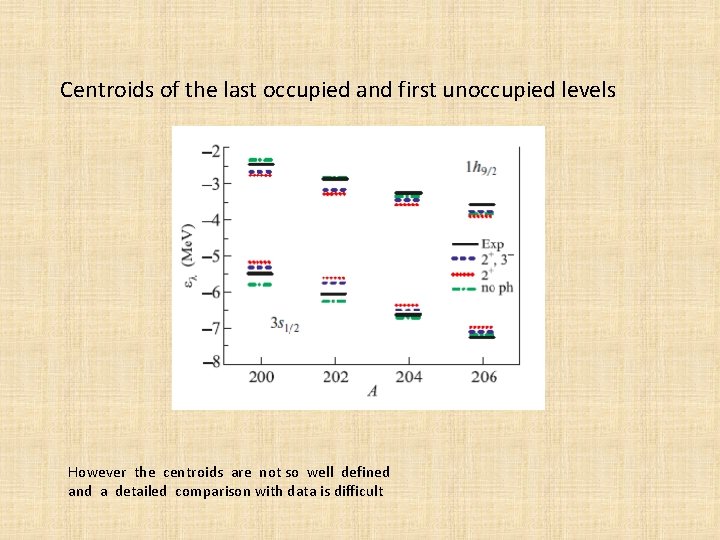
Centroids of the last occupied and first unoccupied levels However the centroids are not so well defined and a detailed comparison with data is difficult

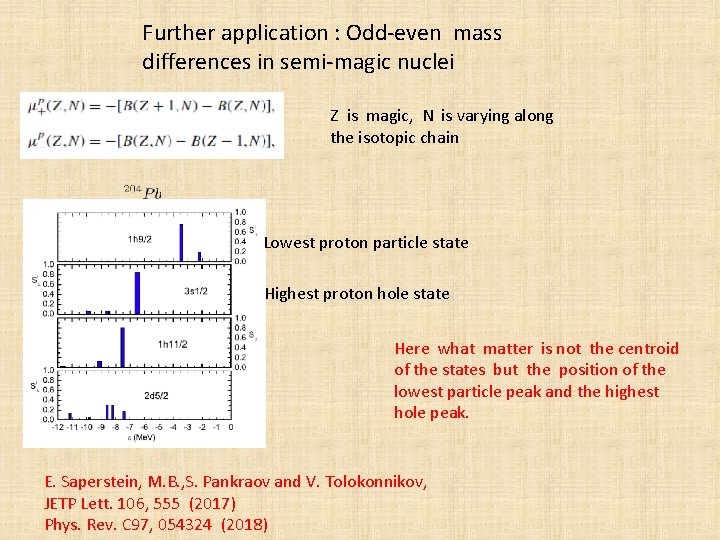
Further application : Odd-even mass differences in semi-magic nuclei Z is magic, N is varying along the isotopic chain Lowest proton particle state Highest proton hole state Here what matter is not the centroid of the states but the position of the lowest particle peak and the highest hole peak. E. Saperstein, M. B. , S. Pankraov and V. Tolokonnikov, JETP Lett. 106, 555 (2017) Phys. Rev. C 97, 054324 (2018)

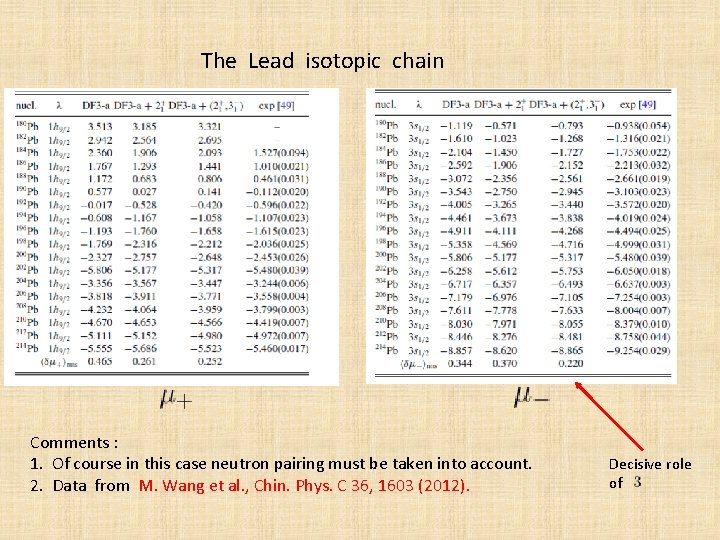
The Lead isotopic chain Comments : 1. Of course in this case neutron pairing must be taken into account. 2. Data from M. Wang et al. , Chin. Phys. C 36, 1603 (2012). Decisive role of

Summary for the TSSF approach 1. For magic heavy nuclei the effect of the particle-phonon coupling improves the energies of the single particle levels 2. For light-medium nuclei there is no improvement. A possible explanation is the approximate treatment of the tadpole term, which is valid for heavy enough nuclei. However, other effects can be missing, see the sequel. 3. For semi-magic nuclei the explicit solution of the Dyson equation is necessary and fragmentation has to be taken in account. Substantial improvement from the particle-phonon coupling. 4. The odd-even double mass differences in semi-magic nuclei can be also improved substantially.

The functional derivative approach In this approach one introduces microscopically the phonon degrees of freedom directly in the equation of motion for the single particle Green’ s function. To this purpose one needs a hamiltonian formalism The normal product is used to avoid contributions of the two-body effective interaction to the Hartree-Fock ground state.

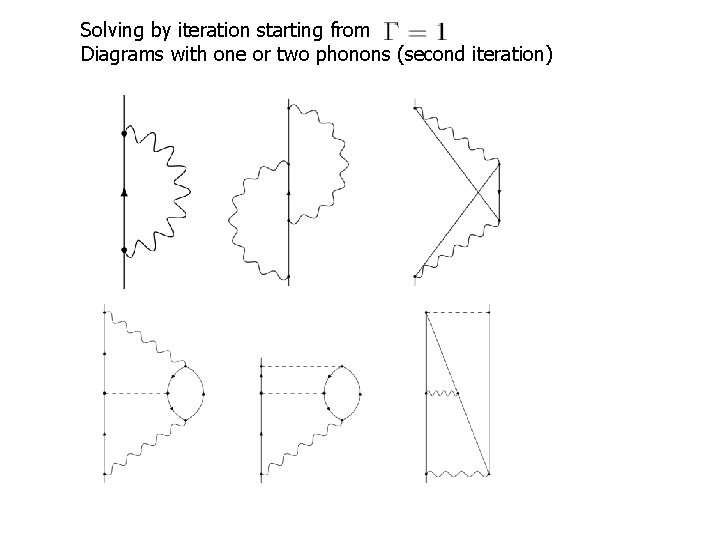
Solving by iteration starting from Diagrams with one or two phonons (second iteration)

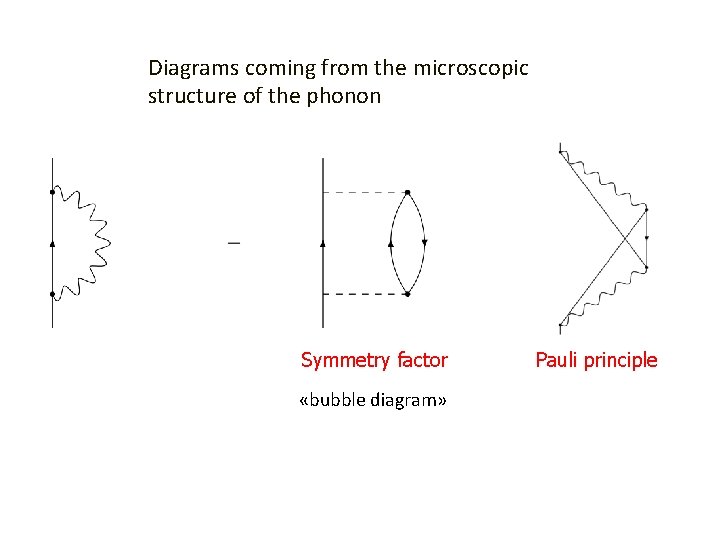
Diagrams coming from the microscopic structure of the phonon Symmetry factor «bubble diagram» Pauli principle

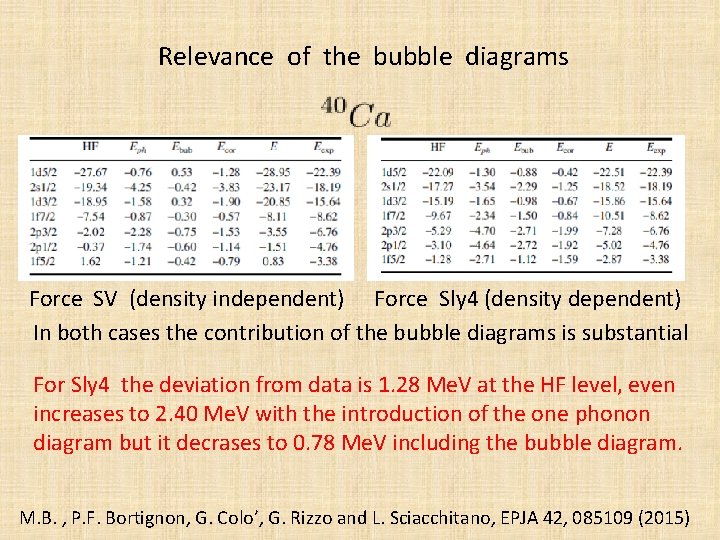
Relevance of the bubble diagrams Force SV (density independent) Force Sly 4 (density dependent) In both cases the contribution of the bubble diagrams is substantial For Sly 4 the deviation from data is 1. 28 Me. V at the HF level, even increases to 2. 40 Me. V with the introduction of the one phonon diagram but it decrases to 0. 78 Me. V including the bubble diagram. M. B. , P. F. Bortignon, G. Colo’, G. Rizzo and L. Sciacchitano, EPJA 42, 085109 (2015)

The tadpole. A comparison. From the functional derivative method one gets the following integral equation for the tadpole U From TFFS one gets a similar result Integral equation for the tadpole S. Kamerdzhiev and S. S. Saperstein EPJA 37, 333 (2008) In this case an additional term is usually included. It comes from the fluctuation of the vertex amplitude, as indicated by the blue circle. In the functional derivative approach it can be obtained from a three-body force, i. e. the third derivative of the functional. M. B. , P. F. Bortignon and E. E. Saperstein, preprint, to be published in EPJA.

Meaning of the tadpole At lowest order one finds (second term only) depletion filling Therefore it is the variation of the static mean field due to the fractional occupation numbers produced by the correlations : Luttinger theorem is therefore satisfied M. B. , P. F. Bortignon and E. E. Saperstein, preprint, to be published in EPJA.

CONCLUSIONS 1. The particle-phonon coupling scheme turns out to be a successful method to go beyond the mean field level, especially for the single particle states in magic and semi-magic nuclei. 2. The functional derivative methods reproduces all terms of the TFFS. 3. In particular the tadpole is related to the variation of the mean field due to the correlations, which imply fractional occupation numbers. Numerical calculations indicate the relevant role of the tadpole. 4. Fragmentation of the single particle states is essential in semi-magic nuclei. 5. In addition to the TFFS terms the functional derivative method introduces other contributions due to the microscopic structure of the phonons. In particular the bubble diagram turns out to be relevant.