Beyond Frequencies Graph Pattern Mining in Multiweighted Graphs

Beyond Frequencies: Graph Pattern Mining in Multiweighted Graphs Giulia Preti Matteo Lissandrini, Davide Mottin, Yannis Velegrakis EDBT 2018, Vienna, Austria

Graphs Social Networks Knowledge Bases 2 EDBT 2018, Vienna, Austria Biological Networks Co-purchase Networks

Graph Pattern Mining 3 EDBT 2018, Vienna, Austria Frequent Pattern

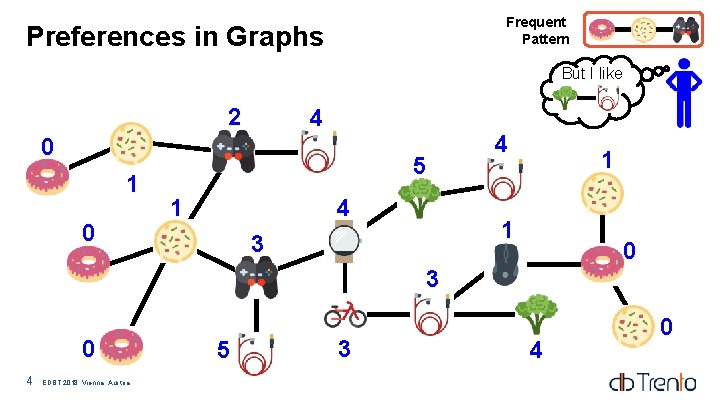
Frequent Pattern Preferences in Graphs But I like 2 4 0 1 0 5 4 1 1 3 0 4 EDBT 2018, Vienna, Austria 5 3 4 0

Related Work Graph Databases Single Graphs Forage [1] Gra. Mi [5] all. Disregard the frequent patterns Sky. Graphweights! [6] skyline patterns structural constraints closed patterns synthetic patterns SPIN [2] Different definition of support! maximal patterns WTMax. Miner [3] maximal weighted frequent patterns user transaction ATW/AW/UBW-g. Span [4] average total weighting affinity weighting utility-based weighting 5 EDBT 2018, Vienna, Austria WIGM [7] weighted graphs Costly to scale! average aggregated weight 1 -extension property

Multiple Users 310 M active users in 2016 6 EDBT 2018, Vienna, Austria

Multiple Users --> Multiple Weights G <V, E, �� > W= {�� 1, �� 2} 25 43 04 51 15 40 How can we find relevant patterns for 310 M users? 15 1 04 4 13 15 33 0 5 31 0 5 7 EDBT 2018, Vienna, Austria 5 5 30 40 0 4

Pattern Mining in Multi-weighted Graphs Which function f ? 8 EDBT 2018, Vienna, Austria

MNI-compatible Functions 9 EDBT 2018, Vienna, Austria

Our Exact Solution 10 EDBT 2018, Vienna, Austria

Computation of the Pattern Score 11 EDBT 2018, Vienna, Austria

What About Multiple Users? 310 M active users in 2016 12 EDBT 2018, Vienna, Austria

Our Approximate Solution Two-step Approach 1. Generate k representative users 1) Create feature vectors 2) Identify similar users 3) Generate maximum-weight vectors 2. Compute k approximate sets of patterns 1) Run Re. Su. M with the representative users Pros Reduced memory consumption Reduced running time 13 EDBT 2018, Vienna, Austria Cons Spurious Patterns

Generate k Representative Users Complete Pattern Sets! 14 EDBT 2018, Vienna, Austria

Bucket-based Strategy 15 EDBT 2018, Vienna, Austria

Quality of the Approximation 16 EDBT 2018, Vienna, Austria

Our MNI-compatible Functions Which isomorphic subgraphs contribute to the pattern score? ALL Subgraphs whose edges have large weights • • You know preferences for almost all the nodes/edges You find only the most relevant patterns ANY Subgraphs with at least one large edge weight • The data is incomplete • You are able to provide some results 17 EDBT 2018, Vienna, Austria

Our MNI-compatible Functions – Cont’ Which isomorphic subgraphs contribute to the pattern score? SUM Subgraphs where the sum of the edge weights is large • • You account for each contribution to value a structure E. g. you consider purchases where the user spent a minimum amount of money AVG Subgraphs with a large average edge weight • You consider patterns with both large-weighted and small-weighted appearances • You return patterns relevant on average 18 EDBT 2018, Vienna, Austria

Experimental Setup 19 EDBT 2018, Vienna, Austria

Frequent vs Relevant Patterns The scoring function affects the patterns returned Frequent patterns upper bound on relevant patterns Relevant patterns reduce information overflow 20 EDBT 2018, Vienna, Austria

Impact of the Scoring Function Performance not worse than FPM 21 EDBT 2018, Vienna, Austria

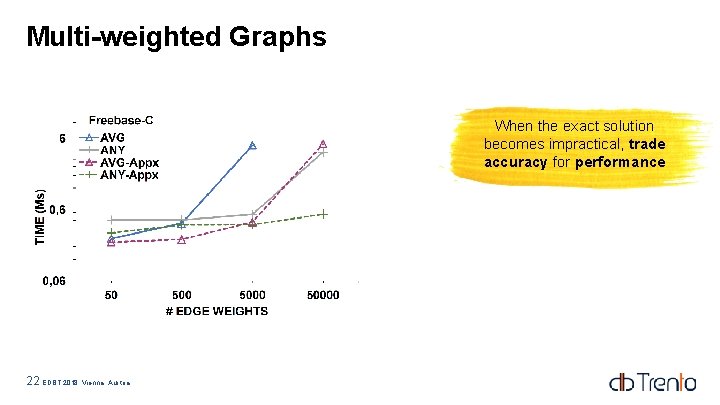
Multi-weighted Graphs When the exact solution becomes impractical, trade accuracy for performance 22 EDBT 2018, Vienna, Austria

Impact of Amount of Weighted Edges Stable performance 23 EDBT 2018, Vienna, Austria

Conclusions We showed that weights are important for graph pattern mining We introduced the problem of pattern mining in large multi-weighted graphs We devised an exact and an approximate solution We proposed four efficient MNI-compatible functions We empirically showed that our approach is scalable and can discover relevant patterns 24 EDBT 2018, Vienna, Austria

Thank you! Questions? gp@disi. unitn. eu 25 EDBT 2018, Vienna, Austria

References [1] F. Pennerath and A. Napoli. Mining frequent most informative subgraphs. In Mining And Learning With Graphs, 2007. [2] Huan, W. Wang, J. Prins, and J. Yang. Spin: mining maximal frequent subgraphs from graph databases. In Proceedings of the 2004 ACM SIGKDD international conference on Knowledge discovery and data mining, pages 581– 586, 2004. [3] R. Geng, X. Dong, P. Zhang, and W. Xu. Wtmaxminer: Efficient mining of maximal frequent patterns based on weighted directed graph traversals. In Cybernetics and Intelligent Systems, 2008 IEEE Conference on, pages 1081– 1086, 2008. [4] C. Jiang, F. Coenen, and M. Zito. Frequent subgraph mining on edge weighted graphs. In Data warehousing and knowledge discovery, pages 77– 88. 2010. [5] M. Elseidy, E. Abdelhamid, S. Skiadopoulos, and P. Kalnis. Grami: Frequent subgraph and pattern mining in a single large graph. Proceedings of the VLDB Endowment, 7(7): 517– 528, 2014. [6] A. N. Papadopoulos, A. Lyritsis, and Y. Manolopoulos. Skygraph: an algorithm for important subgraph discovery in relational graphs. Data Mining and Knowledge Discovery, 17(1): 57– 76, 2008. [7] J. Yang, W. Su, S. Li, and M. M. Dalkilic. Wigm: Discovery of subgraph patterns in a large weighted graph. In SDM, pages 1083– 1094, 2012. [8] Bjorn Bringmann and Siegfried Nijssen. 2008. What is frequent in a single graph? . In PAKDD. 858– 863. 26 EDBT 2018, Vienna, Austria