Beyond CPCTC Lesson 3 4 Medians Every triangle

Beyond CPCTC Lesson 3. 4

Medians: Every triangle has 3 medians A median is a line segment drawn from any vertex to the midpoint of its opposite side. A median bisects the segment.

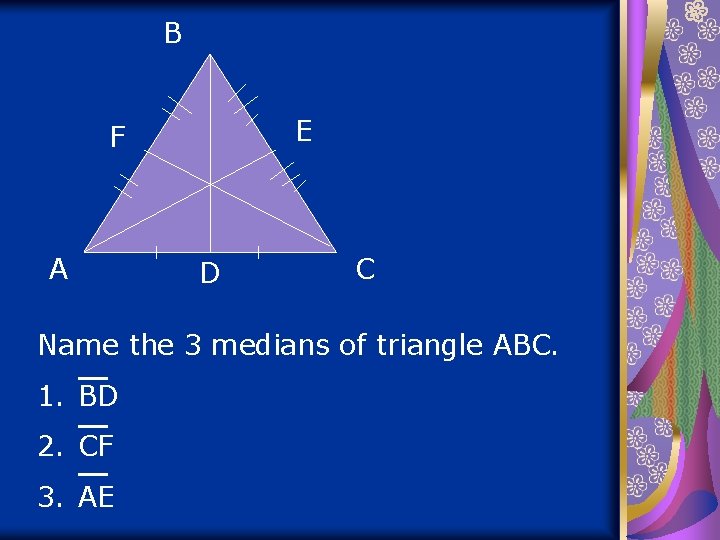
B E F A D C Name the 3 medians of triangle ABC. 1. BD 2. CF 3. AE

Altitudes: Every triangle has 3 altitudes. An altitude is a line segment drawn perpendicular from any vertex to its opposite side. *The altitude could be drawn outside the triangle to be perpendicular. Altitudes form right angles 90˚ You may need to use auxiliary lines (lines added)

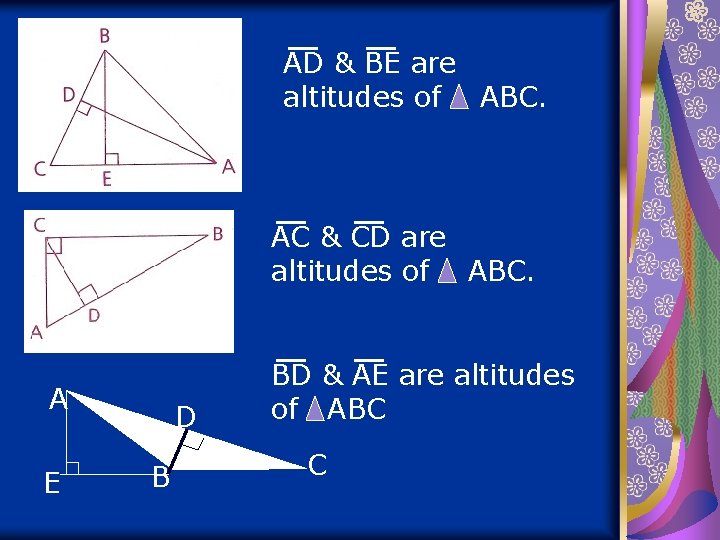
AD & BE are altitudes of ABC. AC & CD are altitudes of ABC. A E D B BD & AE are altitudes of ABC C

Could an altitude also be a median? Yes, for an isosceles triangle when drawn from the vertex.

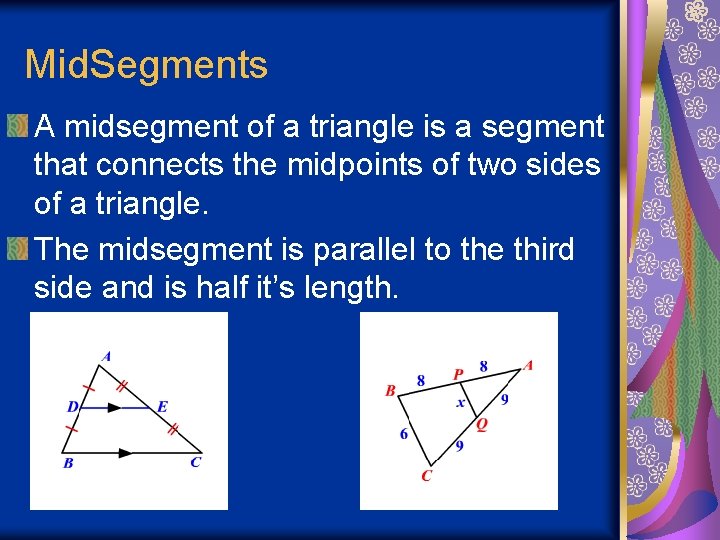
Mid. Segments A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle. The midsegment is parallel to the third side and is half it’s length.

Postulate: Two points determine a line, ray or segment. Determine (one and only one line)

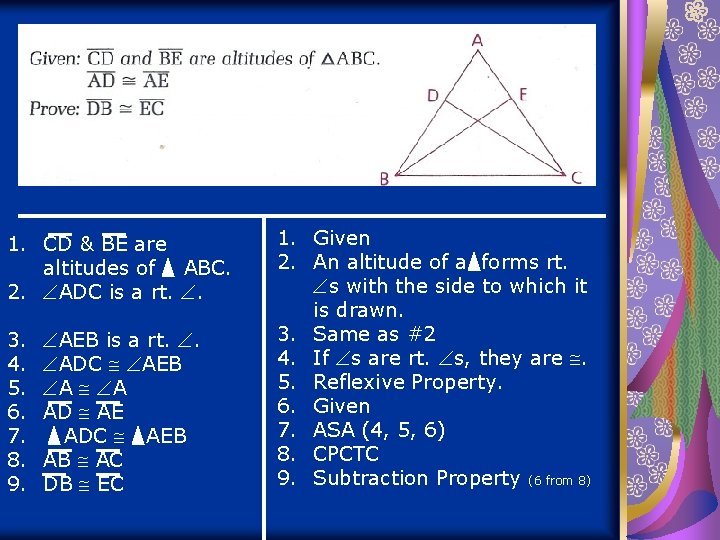
1. CD & BE are altitudes of ABC. 2. ADC is a rt. . 3. 4. 5. 6. 7. 8. 9. AEB is a rt. . ADC AEB A A AD AE ADC AEB AB AC DB EC 1. Given 2. An altitude of a forms rt. s with the side to which it is drawn. 3. Same as #2 4. If s are rt. s, they are . 5. Reflexive Property. 6. Given 7. ASA (4, 5, 6) 8. CPCTC 9. Subtraction Property (6 from 8)