Bevezets a szmtgpi grafikba 1 2 3 Bevezets

Bevezetés a számítógépi grafikába 1. 2. 3. Bevezetés: A Számítógépi grafika tárgya Képek raszteres kódolása Képek geometrikus kódolása, a geometrikus grafika alapjai 4. Koordináta-rendszerek és transzformációk 5. 6. 7. 8. Vetületi ábrázolások A 3 D grafikai alapjai: térbeli alakzatok és színterek képének előállítása Valószerű képek előállítása Egyebek

4. Koordináta-rendszerek és transzformációk 4. 0. Korábban tanultak fölidézése 4. 1. A Descartes-féle derékszögű koordináta-rendszer 4. 2. Homogén koordináták 4. 3. Az egyenes és a sík egyenlete 4. 4. Affin és projektív transzformációk 5. Vetületi ábrázolások 6. A 3 D grafika alapjai http: //digitus. itk. ppke. hu/~krammer/grafika/jegyzet/ http: //krammer. web. elte. hu/eltettk/grafika/jegyzet/

4. 0. Korábban tanultak fölidézése • Ekvivalencia-osztályok • Geometriai vektorok a Descartes-féle koordináta-rendszerben • Lineáris terek (vektor-terek) • Metrikus tér • Az euklideszi tér En • Vektor szorzása mátrixal • Mátrix szorzása mátrixal

Ekvivalencia-osztályok • Ekvivalencia-reláció: olyan reláció a, b H között, amely: reflexív: a ¤ a, szimmetrikus: ha a ¤ b, akkor b ¤ a tranzitív: ha a ¤ b és b ¤ c, akkor a ¤ c • Például: a egyenes párhuzamos b egyenessel • Ekvivalencia-osztály: H 1 H ekvivalencia osztálya a –nak a ¤ reláció szerint : ha a-val együtt minden b ¤ a benne van H 1 -ben és csak azok vannak benne. • Például: az egymással párhuzamos egyenesek halmaza. Például: az egymással arányos számpárok halmaza: { (h*a, h*b); h ≠ 0 }

Geometriai vektorok • Definíció: az irányított szakaszokat vektoroknak nevezzük. (Irányított: egyik végpontját kiválasztjuk kezdőpontnak. ) • Egy vektor állása: egyenesének állása irányítottsága: K->V, vagy V->K iránya: állása és irányítottsága • Egy vektor hossza: a KV távolság; jelölése: |v| V v K

Műveletek geometriai vektorokkal • a = b, ha irányuk és hosszuk megegyezik. Figyelem: nincs helyhez kötve (fizikában néha) • c = a + b : láncszabály, parallelogramma szabály • c = a - b : a közös pontból indított b végéből a végébe. • 0: nullvektor; hossza 0, iránya bármi lehet (!) • l a: állása = a állásával, hossza |l| |a|, irányítottsága megegyezik, vagy ellenkező. • -a: hossza megegyezik, irány ellentétes a-val.

Műveletek geometriai vektorokkal • a b = |a| |b| cos f; szám, 0 f p • a × b = ( |a| |b| sin f ) n 0; 0 f p; (a térben) • a b = 0, ha merőlegesek egymásra, a × b = 0, ha párhuzamosak egymással, különben a × b = n; a síkjukra merőleges vektor (a térben)

Geometriai vektorok a Descartes-féle koordináta-rendszerben • A P pont helyvektora: az OP vektor • Ennek koordinátás alakja a (px, py, pz) számhármas • Műveletek: a számpárok algebrája: (a, b, c) ± (d, e, f) = (a ± d, b ± e, c ± f) (0, 0, 0) a nullelem l (a, b, c) = (l a, l b, l c) (a, b, c) (d, e, f) = (a d + b e + c f); szám (a, b, c) × (d, e, f) = | i j k | = (bf-ce, -af+cd, ae-bd) |abc| |def |

Lineáris terek (vektor-terek) • Matematikai absztrakció • Az L halmazt a K számtest fölötti lineáris térnek nevezzük, ha az a, b, g K és a, b, c L elemekkel: 1. minden a, b elemmel létezik egy (a, b) -> c hozzárendelés, amelyet összeadásnak nevezünk és c = a + b –vel jelölünk, 1. 1. amely kommutatív: a + b = b + a 1. 2. és disztributív: (a + b) + c = a + (b + c) 1. 3. amelyhez létezik nullelem: a + 0 = a minden a L –re 1. 4. minden a L –nek létezik inverze: -a + a = 0

Lineáris terek (vektor-terek) • 2. Minden a K és a L –hez létezik b L : b = a a 2. 1. 1 a = a ; (1 K ) 2. 2. (a b) a = a (b a) • 3. 1. (a + b) a = a a + b a 3. 2. a (a + b) = a a + a b • - A geometriai vektorok halmaza - a valós számpárok (szám n-esek) halmaza - {pk(x); k n}, a legfeljebb n-edfokú polinómok halmaza - {f(x); f(x) : [a, b] - > R, f(x) folytonos} halmaz - stb.

Metrikus tér • Olyan lineáris tér, amelyben értelmezve van bármely két elem távolsága, és erre: d(a, b) 0 d(a, b) = d(b, a) d(a, b) = 0, „acsaha” a=b d(a, b) d(a, c) + d(c, b)

Az euklideszi tér E n • A geometriai vektorok tere: metrikus tér • A valós számpárok (szám n-esek) tere is metrikus tér; d = (x 2 -x 1)2+(y 2 -y 2)2+… • Ezek „izomorfak”; szóhasználatunkban egy vektor lehet ez is – az is. • Izomorfia (egyező szerkezetűség): két tér izomorf, ha van közöttük egy-egyértelmű, művelettartó megfeleltetés

Vektor szorzása mátrixal • Az X pont helyvektora: X = (x, y, z)T nálam oszlopvektor (de a T-t általában elspórolom) • • X’ = A 33 X = ( a 11 a 12 a 13 ) (x) = | a 21 a 22 a 23 | |y| ( a 31 a 32 a 33 ) (z) = ( a 11 x + a 12 y + a 13 z ) = (x’) | a 21 x + a 22 y + a 23 z | = |y’| ( a 31 x + a 32 y + a 33 z ) = (z’)

Mátrix szorzása mátrixal C 33 = A 33 B 33 = ( a 11 a 12 a 13 ) ( b 11 b 12 b 13 ) | a 21 a 22 a 23 | | b 21 b 22 b 23 | ( a 31 a 32 a 33 ) ( b 31 b 32 b 33 ) c 11 = a 11 b 11 + a 12 b 21 + a 13 b 31 c 12 = a 11 b 12 + a 12 b 22 + a 13 b 32 c 13 = a 11 b 13 + a 12 b 23 + a 13 b 33 c 21 = a 21 b 11 + a 22 b 21 + a 23 b 31. . . cik = ai 1 b 1 k + ai 2 b 2 k + ai 3 b 3 k = ai* b*k

4. Koordináta-rendszerek és transzformációk 4. 0. Korábban tanultak fölidézése 4. 1. A Descartes-féle derékszögű koordináta-rendszer 4. 2. Homogén koordináták 4. 3. Az egyenes és a sík egyenlete 4. 4. Affin és projektív transzformációk

4. 1. A Descartes-féle derékszögű koordináta-rendszer • Pontok és vektorok típusának definíciója • A síkbeli polárkoordináta-rendszer • Gömbkoordináta-rendszer, térbeli polár-koordináták • Baricentrikus koordináták

A Descartes-féle, derékszögű koordináta-rendszer • Meghatározza: a kezdőpont (origó), a 3 tengely állása és egy térbeli egységpont • A pontok: P = [x, y, z]T (nálam: oszlopvektor) • Kétféle irányítása lehet (szemléletesen): jobbsodrású (jobbos, jobbkezes): a Z végéből nézve … balsodrású (balos, balkezes)

A síkban: § Meghatározza: a kezdőpont (origó), a 2 tengely állása és egy térbeli egységpont § Pontok: P = [x, y]T (oszlopvektor) § Kétféle irányítás lehet (szemléletesen): jobbsodrású (jobbos, jobbkezes): az órajárással ellentétesen balsodrású (balos, balkezes)

Pontok és vektorok típusának definíciója § a pont és a vektor típus egyaránt számhármas (számpár): type Gxyz = Real; {vagy Double} type Point 2 = record x, y : Gxyz; end; type Vector 2 = record x, y : Gxyz; end; § Vector 2 műveletei: u = v, u ± v, l u, u v, |u| § Point 2 műveletei: P = Q (és több nincs!) § Szigorú típus ellenőrzés és szerep kényszer (cast) s: = Point 2( (Vector 2(P)+Vector 2(Q))/2 ); § Vegyes típusú műveletek: P 2 = P 1 + v; {a P 1 pont eltolása a v vektorral} v = P 2 – P 1, {vektor a P 1 -ből a P 2 -be}

Pontok és vektorok C-ben •

A síkbeli polárkoordináta-rendszer § A kezdőpont, a polár-tengely, a pozitív elfordulás iránya. § P polár-koordinátái: P=(r, f); (0 r), (0 f<2 p). § polár-koordináták Descartes koordináták: x = r*cos f, és y = r*sin f § Descartes koordináták polár-koordináták: r = x 2+y 2 és f = arctan(y/x), ha sem x sem y nem 0, = 0, ha y=0 és x>0 = p, ha y=0 és x<0 = +p/2, ha x=0 és y>0 = -p/2, ha x=0 és y<0 = meghatározatlan, ha x=y=0 (a kezdőpont).

Gömbkoordináta-rendszer, térbeli polár-koordináták § Alapsík, benne PKR és a Z tengely. § gömbkoordináták: P=(r, f, q); (0 r), f: a polárszög (0 f 2 p, az alapsíkban) q azimut, (0 q p) § henger-koordináták: (r, f, z) § polár-koordináták derékszögű koordináták: r=r*sin q= x 2+y 2, (az alapsíkban) x= r *cos f =r*sin q *cos f; y= r *sin f =r*sin q *sin f, z=r*cos f § derékszögű koordináták Polár-koordináták : . . .

Baricentrikus koordináták § a 0, a 1, …, an En ; kifeszítik az (n-1) dimenziós teret § minden x En -hez egyértelműen létezik {l 0, l 1, …ln} valósak: x = l 0 a 0 + l 1 a 1 +…+ lnan; § Ha Sli =1. (lehetnek negatívok is): {li}: az x {ai}-re vonatkozó baricentrikus koordinátái § Tömegpontok súlypontja: li > 0 (térben 4, síkban 3, egyenesen 2 alappont) § Ha x baricentrikus koordinátái pozitívak, akkor x az {ai} alappontok konvex burkán belül van.

4. Koordináta-rendszerek és transzformációk 4. 0. Korábban tanultak fölidézése 4. 1. A Descartes-féle derékszögű koordináta-rendszer 4. 2. Homogén koordináták 4. 3. Az egyenes és a sík egyenlete 4. 4. Affin és projektív transzformációk

4. 2. Homogén koordináták • Az E 2 egy „inhomogenitása” • • • A kibővített euklideszi sík Az euklideszi tér kibővítése Homogén koordináták „Homogén terünk” szerkezete Homogén -> Descartes koordináták A sík homogén koordinátás egyenlete • Miért használunk homogén koordinátákat? • Áttérés a homogén alakra és visszatérés
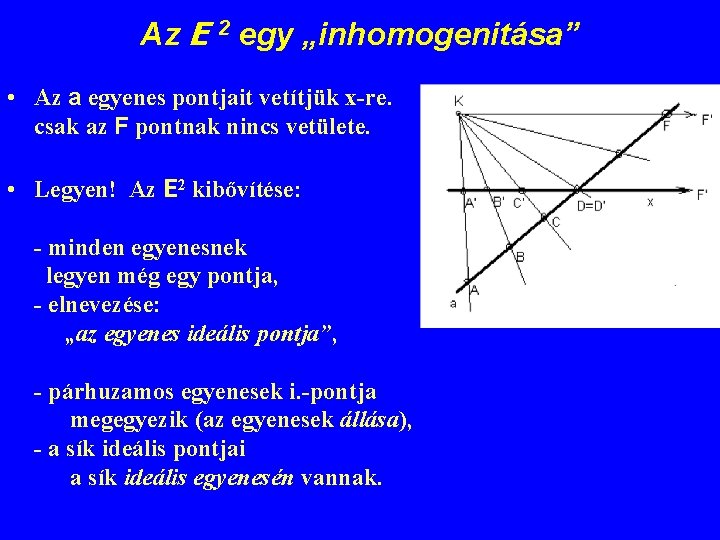
Az E 2 egy „inhomogenitása” • Az a egyenes pontjait vetítjük x-re. csak az F pontnak nincs vetülete. • Legyen! Az E 2 kibővítése: - minden egyenesnek legyen még egy pontja, - elnevezése: „az egyenes ideális pontja”, - párhuzamos egyenesek i. -pontja megegyezik (az egyenesek állása), - a sík ideális pontjai a sík ideális egyenesén vannak.

A kibővített euklideszi sík • Az E 2 projektív lezárása (a „kibővített sík”); projektív sík egy kitüntetett egyenessel. • Én „a homogén sík”-nak nevezem: H 2 = E 2 U I 2. • A projektív síkban: bármely két pont meghatároz egyenest bármely két egyenes meghatároz egy pontot …

Az euklideszi tér kibővítése § A tér minden egyenesének (közönséges pontjain kívül) még egy pontot tulajdonítunk; „az egyenes ideális pontja”, olymódon, hogy: § párhuzamos egyenesek ideális pontja megegyezik; (ezek állása), § egy sík ideális pontjai egyenesen vannak, „a sík ideális egyenese”, § párhuzamos síkok ideális egyenese megegyezik, § a tér ideális egyenesei egy síkban vannak, „a tér ideális síkja”

Homogén koordináták • A tér egy derékszögű koordináta-rendszerében … • KR kezdőpontja közönséges pont • (x, y, z) közönséges pont [x, y, z, 1] homogén koordináták, illetve az ezzel arányos számnégyesek bármelyike: (x, y, z) [x, y, z, 1] h [x, y, z, 1] = = [h x, h y, h z, h]; h 0 • Arányos számnégyesek ekvivalencia-osztálya

„Homogén terünk” szerkezete • Az euklideszi tér izomorf a valós számhármasok terével: E 3 ~= R 3 = {(x, y, z); x, y, z R} • Az egymással arányos valós számnégyesek ekvivalencia-osztályai; adott (x, y, z, w) R 4 esetén: Ax, y, z, w = { [x·h, y·h, z·h, w·h]; h R, h≠ 0} • A homogén tér az ilyenek halmazával izomorf: H 3 ~= {Ax, y, z, w ; x, y, z, w R} {[0, 0, 0, 0]}

Homogén -> Descartes koordináták • Fordítva, a kibővített tér [x 1, x 2, x 3, h] pontjának : – ha h 0, akkor ez közönséges pont és Descartes-koordinátái: [x 1, x 2, x 3, h] [x 1/h, x 2/h, x 3/h, 1] (x 1/h, x 2/h, x 3/h), – ha h=0, de x 1, x 2, x 3 nem mind nulla, akkor [x 1, x 2, x 3, 0] ideális pont, és x 1, x 2, x 3 a rá illeszkedő egyenesek állását (irány-koszinuszait) határozzák meg, – [0, 0, 0, 0] nem pont (számítások eredménye nem lehet).

A sík homogén koordinátás egyenlete • Egy P pont homogén(-koordinátás) alakja (h≠ 0): P = [p 1, p 2, p 3, p 4]T h·[p 1, p 2, p 3, p 4]T; pi nem mind nulla • Egy s sík homogén(-koordinátás) alakja (h≠ 0): s = [s 1, s 2, s 3, s 4] h·[s 1, s 2, s 3, s 4]; si nem mind nulla • Az s sík egyenlete: az s minden P pontjára: s · P = 0, azaz: s 1·p 1+s 2·p 2+s 3·p 3+s 4·p 4 = 0 • Az ideális sík homogén alakja: [0, 0, 0, c ]; c 0 (Minden pontja ideális pont: [x, y, z, 0] )
![Nevezetes pontok homogén koordinátái • Bármilyen c 0 számmal [0, 0, 0, c] az Nevezetes pontok homogén koordinátái • Bármilyen c 0 számmal [0, 0, 0, c] az](http://slidetodoc.com/presentation_image_h/ab34bd243b0176115c2bc86c601f7ef6/image-33.jpg)
Nevezetes pontok homogén koordinátái • Bármilyen c 0 számmal [0, 0, 0, c] az origó homogén alakja, [c, 0, 0, 0] az X tengely ideális pontja, [0, c, 0, 0] az Y tengely ideális pontja, [0, 0, c, 0] a Z tengely ideális pontja, • [0, 0, 0, c] az ideális sík, [c, 0, 0, 0] az YZ (z=0) koordináta-sík; pontjai: [0, x, y, h], [0, c, 0, 0] az XY sík, [0, 0, c, 0] az XY sík homogén alakja.

Miért használunk homogén koordinátákat? • A számításokban föloldják a nem metsző párhuzamosok „kivételes” helyzetét. • A mátrix szorzás egységes formalizmusa (eltolás!), • Transzformációk egymásutánja: mátrixuk szorzata • A középpontos vetítés nem affin transzformáció; 4 x 4 -es mátrix-al és a pontok homogén alakjával adható meg

Áttérés a homogén alakra és visszatérés • Feladataink Descartes-koordinátákkal adjuk meg és az eredményeket ugyanígy várjuk. 1. 2. 3. 4. áttérés homogén koordinátákra: (x, y, z) [x, y, z, 1]. . . A „kényes” műveletek homogén alakban … az eredmények „szűrése” (ideális pontok kizárása) visszatérés (projektív osztás): [x 1, x 2, x 3, x 4] (x 1/x 4 , x 2/x 4, x 3/x 4). így értékeljük az eredményeket. 5.

4. Koordináta-rendszerek és transzformációk 4. 0. Korábban tanultak fölidézése 4. 1. A Descartes-féle derékszögű koordináta-rendszer 4. 2. Homogén koordináták 4. 3. Az egyenes és a sík egyenlete 4. 4. Affin és projektív transzformációk

4. 3. Az egyenes és a sík egyenlete • Az egyenes egyenlete • Félsík megadása (E 2) • Számítási feladatok • A sík egyenlete (a térben) • Számítási feladatok

Az egyenes egyenlete a síkban • Az egyenes homogén, implicit egyenlete (E 2): a·x + b·y + c = 0; a 2+b 2 0; egyenes megadása: (a, b, c); a 2+b 2 0; • Homogén koordinátákkal (H 2): a·x + b·y + c·w = 0; a 2+b 2 0; egyenes megadása: [a, b, c] h·[a, b, c]; a 2+b 2 0; • A homogén egyenlet Hesse-féle normál alakja (E 2): a’·x + b’·y + c’=0; a’ 2+b’ 2=1; (-1 ≤ a’, b’ ≤ +1; )

Az egyenes egyenlete a síkban (2) • Az egyenes „iskolai egyenlete” (E 2): y = M · x + B; csak ha B 0 ! • Két adott pontján át: (x 2 -x 1) · (y-y 1) = (y 2 -y 1) · (x-x 1) • illetve, ha x 1 x 2 : y = ( (y 2 -y 1)/(x 2 -x 1) ) · (x- x 1) + y 1 = M· (x- x 1) + y 1 • Adott pont, adott irány: b’· (y-y 1) = -a’ · (x-x 1); • illetve, ha b’ 0 : y = M · (x- x 1) + y 1 ; M = a’/b’

Az egyenes egyenlete a síkban (3) • Determináns alakban, adott P=(px, py) és Q=(qx, qy) pontokkal (E 2): | x y 1 | = 0 | px py 1 | | qx qy 1 | (az első sora szerint kifejtve …) • Normálvektoros egyenlet: adott R pontja és n normálvektora (E 2); (X - R) · n = 0, azaz: (x-rx)·nx+(y-ry)·ny = 0, azaz: X·n=R·n x·nx+y·ny=rx·nx+ry·ny

Az egyenes paraméteres egyenlete (E 2, E 2) • Adott (a síkban, vagy a térben) P és Q pontja: X = P + t·(Q-P), átrendezve: X = (1 -t)·P + t·Q, azaz: x = px + t·(qx-px) átrendezve: x = (1 -t)·px + t·qx, y = py + t·(qy-py), átrendezve: y = (1 -t)·py + t·qy, z = pz + t·(qz-pz), átrendezve: z = (1 -t)·pz + t·qz. t=0: a P pont, t=1: a Q pont , 0 t 1: a szakasz pontjai, t 0: P oldalán kívül, t 1: Q oldalán kívül egyenlőközű t értékek: egyenlőközű pontok, t és (1 -t): baricentrikus koordináták az egyenesen

Félsík megadása (E 2) • Egyenlőtlenséggel: a·x + b·y + c < 0; a 2+b 2 0; • Határ-egyenesével és egy pont a félsíkban • A határ-egyenes egy pontja és normálvektora (R, n) n R R

A sík implicit, homogén egyenlete • A sík homogén, implicit egyenlete (E 3): a·x+b·y+c·z+d=0; a 2+b 2+c 2 0 Egy sík megadása: [a, b, c, d]; a 2+b 2+c 2 0 • Homogén alakban (H 3): a·x+b·y+c·z+d·z=0; a 2+b 2+c 2 0 Egy sík megadása: [a, b, c, d] h·[a, b, c, d]; a 2+b 2+c 2 0 • A sík Hesse-féle normálegyenlete (E 3): a’·x+b’·y+c’·z+d’=0; a’ 2+b’ 2+c’ 2=1 (-1 ≤ a’, b’, c’ ≤ +1)

A homogén egyenlet determináns alakja (E 3): • Három nem egyenesbe eső adott pont: P = (px, py, , pz, ), Q = (qx, qy, qz, ), R = (rx, ry, rz, ): | | x px qx rx y py qy ry z pz qz rz 1 1 | = 0 | | | A determinánst az első sora szerint kifejtve: ax + by + cz + d = 0

A sík normálvektoros egyenlete (E 3): • A sík adott P pontja és n normálvektora: (X - P)·n = 0, illetve: (x-px) · nx+(y-py) · ny+(z-pz) · nz = 0; X·n = P·n, pz·nz illetve: x·nx+ y·ny+ z·nz = px·nx+ py·ny+

A sík paraméteres egyenlete (E 3): • A síkot kifeszítő u, v vektor párral és P pontjával: X = P + s · u + t · v, és a koordinátákra: • A sík három, nem egyenesbe eső P, Q és R pontjával X = Q + s·(P-Q)+ t·(R-Q), vagy: X = (1 -s-t)·Q + s·P+t·R x = qx + s·(px-qx)+t·(rx-qx), vagy: x = (1 -s-t)·qx +s·px+t·rx y = qy + s·(py-qy)+t·(ry-qy), vagy: y = (1 -s-t)·qy +s·py+t·ry z = qz + s·(pz-qz)+t·(rz-qz), vagy: z = (1 -s-t)·qz +s·pz+t·rz. • ha 0 s, t, 1 -s-t 1 : a háromszög pontjai, ha közülük egy nulla: a háromszög egyik oldala, ha kettő nulla (és a harmadik 1): egyik csúcsa, ha valamelyik negatív, vagy >1: a pont kívül van. • s, t, 1 -s-t : baricentrikus koordináták a síkban

Számítási feladatok – Példa: két egyenes metszéspontja A két egyenes paraméteres egyenletét kielégíti a közös X=(x, y) metszéspont; négy egyenlet, négy ismeretlen: x, y, t, t’ – A térben két egyenes lehet kitérő is! A metszési feladatot, először pl. z = 0 -lal az XY síkra oldjuk meg; vagy jó, vagy nem jó! – Egyenes metszéspontja szakasszal; 0 t 1 – Egyenes döféspontja egy térbeli háromszöggel (E 3) Az egyenes és sík paraméteres egyenlete, 3 ismeretlen; ha a háromszögön belül, akkor 0 s, t, 1 -s-t 1

Jegyzet A 4. Fejezethez: G 4@D-…. rtf, Gi 41 -3 E-…. ppt (ez az előadás) Gi 43 F-Számítási feladatok. ppt
- Slides: 48