Better Than Average Finding Geometric Means Using SAS

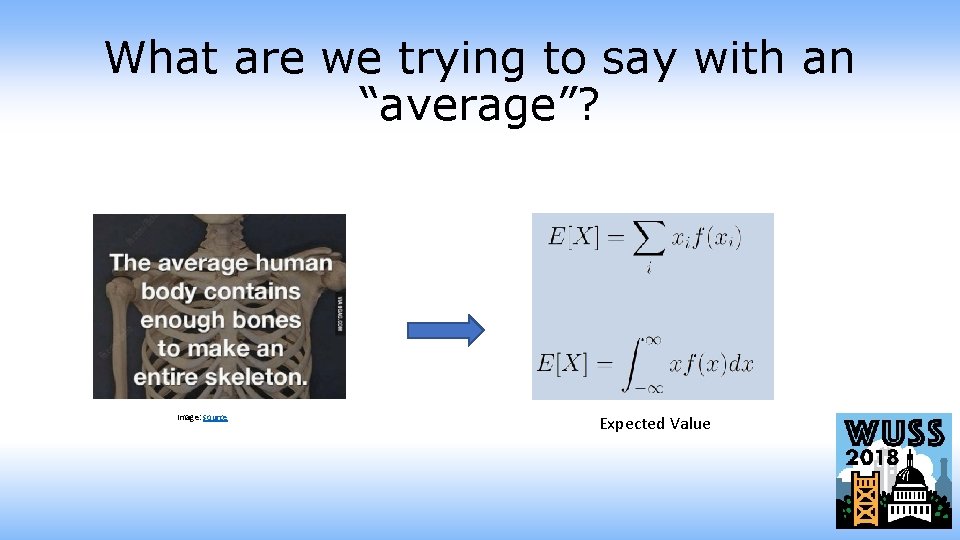
What are we trying to say with an “average”? Image: source Expected Value

Common Types of “Averages” Median: Middle element of ordered data Mode: Value most often seen in a data set § Main advantages: not influenced by extreme values, can be used for any type of distribution § Main disadvantage: Insensitive, gives no information about your distribution Images: source

Common Types of “Averages” Arithmetic Mean: Calculated from the sum of values divided by the number of values in a data set § Main advantages: Easy to understand uses all observations, can give information about your distribution § Main disadvantages: Easily skewed by outliers and inaccurate if working with non-Normal data Image: source

What is a geometric mean? Geometric Mean: Calculated by taking the nth root of the product of n positive observations in a data set § Main advantages: Precise, but not influenced by extreme values § Main disadvantages: More difficult to understand, all values must be non-zero and positive Image: source

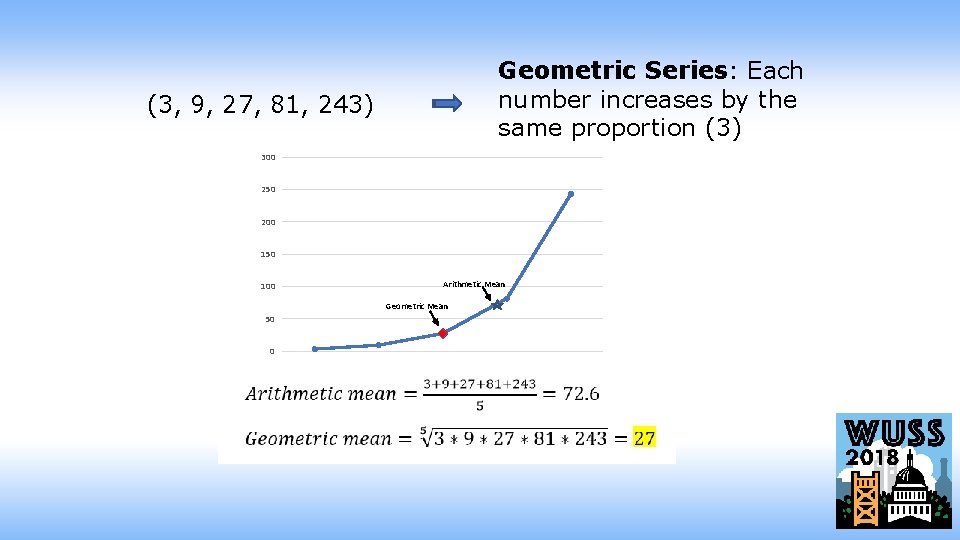
Geometric Series: Each number increases by the same proportion (3) (3, 9, 27, 81, 243) 300 250 200 150 100 Arithmetic Mean Geometric Mean 50 0

When should I use the geometric mean? • Non-Normal/skewed data • Ratios or proportions/scaled data • Small sample sizes Source

Bioassays/dose-response curves Image source Population growth Image source Compounding interest Image source Decay rates Image source Scaled bioequivalence Image source Survival analysis Image source

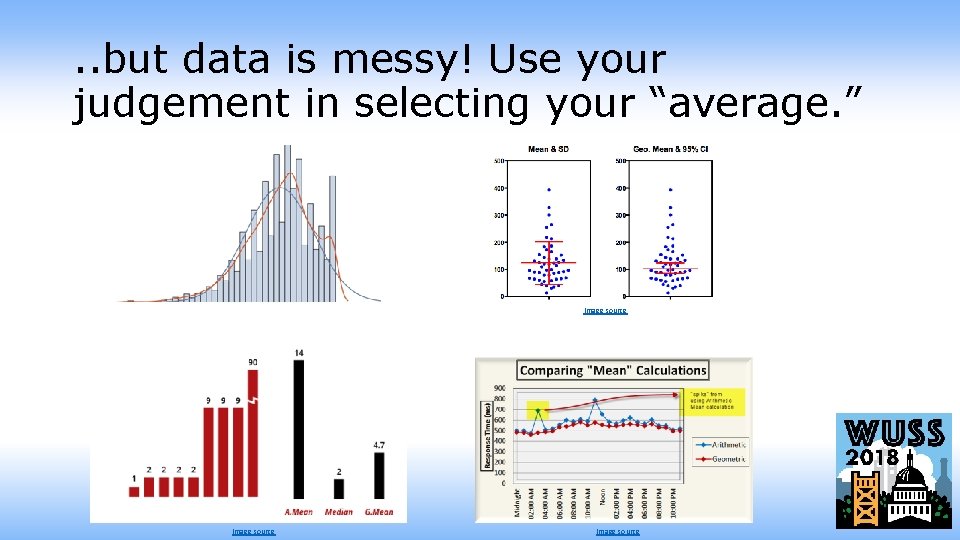
. . but data is messy! Use your judgement in selecting your “average. ” Image source

What if my data contains zeroes? • Adjust your scale so that you add 1 to every number in the data set, and then subtract 1 from the resulting geometric mean. • Ignore zeros or missing data in your calculations. • Convert zeros to a very small number (often called “below the detection limit”) that is less than the next smallest number in the data set.

• If all values are negative, simply convert all values to positive numbers before calculating the geometric mean. Then assign the resulting geometric mean a negative value. • If your data set contains both positive and negative values, you will have to separate them and find the geometric means for each group, and you can then find the weighted average of their individual geometric means to find the total geometric mean for the full data set.

How can I use SAS to compute geometric means? • Geomean() or Geomeanz() functions • PROC SURVEYMEANS • Manual calculations Source

Finding the geometric mean for an observation/row: Geomean() or Geomeanz() Functions Returns the geometric mean of a numeric constant, variable, or expression • If any arguments are negative, result is a missing value • If any arguments are zero, result is zero • Fuzzes the values of arguments that are extremely small and approximately zero—if you do not want this, use the geomeanz() function • Skips missing values

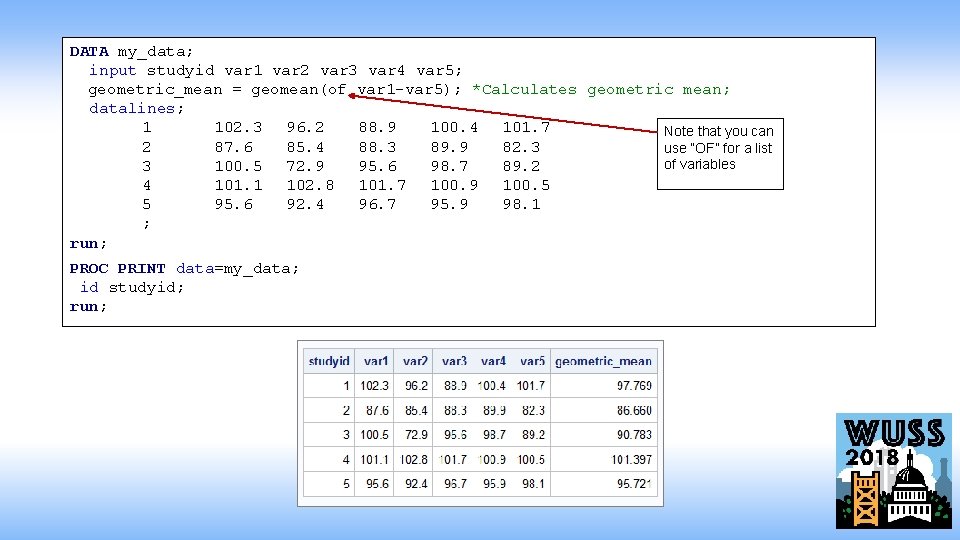
DATA my_data; input studyid var 1 var 2 var 3 var 4 var 5; geometric_mean = geomean(of var 1 -var 5); *Calculates geometric mean; datalines; 1 102. 3 96. 2 88. 9 100. 4 101. 7 Note that you can 2 87. 6 85. 4 88. 3 89. 9 82. 3 use “OF” for a list of variables 3 100. 5 72. 9 95. 6 98. 7 89. 2 4 101. 1 102. 8 101. 7 100. 9 100. 5 5 95. 6 92. 4 96. 7 95. 9 98. 1 ; run; PROC PRINT data=my_data; id studyid; run;

Finding the geometric mean for a population/column: PROC SURVEYMEANS The geomean option within PROC SURVEYMEANS returns the geometric mean of the specified variables. *Values must be non-zero and positive You can also request confidence limits for the geometric mean § GMCLM requests the 2 -sided confidence limits § LGMCLM requests the 1 -sided lower confidence limit § UGMCLM requests the 1 -sided upper confidence limit

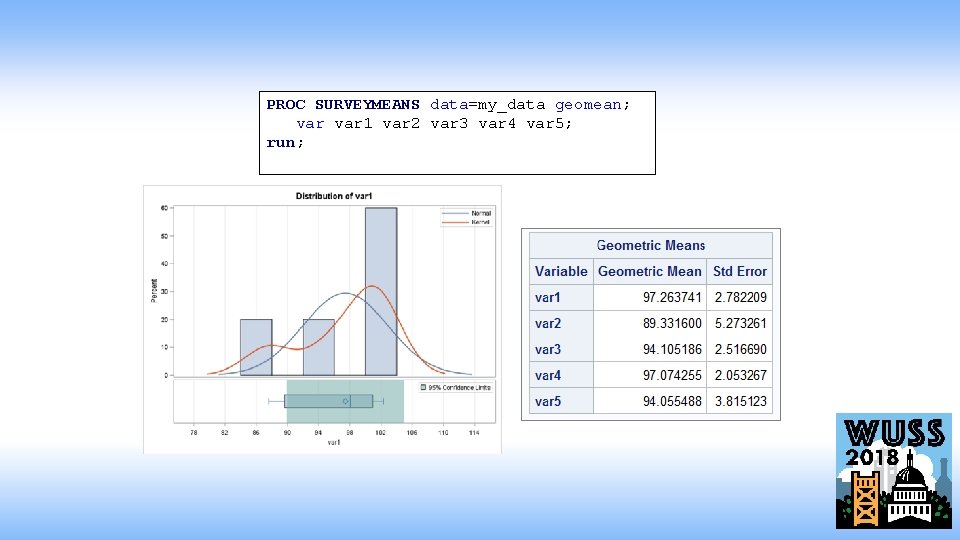
PROC SURVEYMEANS data=my_data geomean; var 1 var 2 var 3 var 4 var 5; run;

Which measure of variation should I use? 1. Standard error: how precise is the calculation of the geometric mean 2. Standard deviation: how spread out is the data around the geometric mean 3. Coefficient of variation: how does the variation for this geometric mean compare with another data set

Geometric Standard Error Output by default in PROC SURVEYMEANS

Geometric Standard Deviation 1. Find the natural log of your variable using the log() function in the DATA step: DATA my_data 2; set my_data; ln_var 1 = log(var 1); *Calculates the natural log of variable 1; run;

Geometric Standard Deviation 2. Use PROC MEANS to find the arithmetic mean and standard deviation of your newly log-transformed variable: PROC MEANS data=my_data 2 mean stddev; *Specifies output; var ln_var 1; output out=meansout mean=a_mean stddev=a_stddev; *Creates new data set; run;

Geometric Standard Deviation 3. Exponentiate the arithmetic mean and standard deviation to find the geometric mean and geometric standard deviation, using the EXP() function in the DATA step: DATA my_data 3; set meansout; geo_mean = exp(a_mean); *Converts to geometric mean; geo_stddev = exp(a_stddev); *Converts to geometric standard deviation; run; PROC PRINT data=my_data 3 noobs; var geo_mean geo_stddev; run;

Applying the Geometric Standard Deviation Geometric Mean ± Geometric Standard Deviation =INCORRECT!

Applying the Geometric Standard Deviation The geometric standard deviation is multiplicative, NOT additive: Lower bound = geometric mean ÷ geometric standard deviation =97. 2637 ÷ 1. 06605 = 91. 2375 Upper bound = geometric mean x geometric standard deviation =97. 2637 x 1. 06605 = 103. 6880 Resulting range for one geometric standard deviation is (91. 24, 103. 69)

Geometric Coefficient of Variation Reduce the geometric standard deviation to the power of the reciprocal of the geometric mean in the DATA step: DATA my_data 4; set my_data 3; geo_cv = geo_stddev**(1/geo_mean); *Calculates geometric CV; run; PROC PRINT data=my_data 4 noobs; var geo_cv; run;

To sum up: Source • Use geometric means for data that is lognormal or uses ratios or proportions • Make sure your values are non-zero and positive • Use your judgement in choosing the mean to express your expected values when working with messy data

Questions?

Contact Information Name: Kimberly Roenfeldt Company: Henry M Jackson Foundation for the Advancement of Military Medicine City/State: San Diego, CA Phone: (619) 767 -4584 Email: kimroenfeldt@gmail. com