Betrachtung der Realitt aus der Sicht der Statistik

Betrachtung der Realität aus der Sicht der Statistik DIE GRUNDLAGEN DER STATISTIK Übersetzung: / Tradotto da: Scuola Secondaria di 1°grado; Argomento: Leggiamo - Basi (30. 14); Pacchetto: S 1. A. 1

INHALT 1) Was untersucht die Statistik? 2) Kollektive Phänomene 3) Merkmale und Ausprägungen 4) Erhebungseinheit und Grundgesamtheit 5) Häufigkeiten (absolute, relative, prozentuelle)… 6) Lagemaße (Modus, Median, Mittelwert) 7) Streuungsmaße (Spannweite)

Was untersucht die Statistik? Die Hauptaufgabe der Statistik besteht darin, das, was in der Masse der Informationen unklar erscheint, verständlich zu machen. Wenn man Informationen zu einem bestimmten Phänomen sammelt, hat man mit sehr vielen unbearbeiteten Daten (Rohdaten) zu tun. Deshalb muss als erstes diese Menge an Rohdaten mit besonders aussagekräftigen Indikatoren zusammengefasst werden. Dazu werden numerische (d. h. mit Zahlen) oder grafische (d. h. bildliche) Methoden verwendet, welche die erhobenen Daten beschreiben können, ohne die gesamte Bedeutung zu verändern.

Kollektive Phänomene Die Statistik beschäftigt sich also mit den Phänomenen, bei denen sehr viele einzelne Ausprägungen (kollektive Phänomene) beobachtet werden müssen, damit man das Phänomen selbst untersuchen kann. Die Statistik fasst diese einzelnen Informationen zusammen. Anders gesagt: Die Statistik versucht, aus einer riesigen Menge an Informationen das Wichtigste herauszufiltern, den Zahlen Gehör zu verschaffen! Ist das aber wirklich nötig? Wäre es nicht besser, alle verfügbaren Informationen einzeln und im Detail anzuschauen?

Braucht es die Statistik? • In einer Mittelschule haben die Lehrer eine Umfrage zu den Reisen und Sommerferien der Schüler gemacht. • Sie haben jeden Schüler gebeten, eine der sechs folgenden Antworten auszuwählen: kein Urlaub, Meer, Berg, Land, Kunststadt, anderes. Meer Kulturstadt Meer Anderes Kulturstadt Berg Kein Urlaub Meer Anderes Kein Urlaub Berg Meer Kein Urlaub Meer Berg Kein Urlaub Meer Land Berg Kein Urlaub Anderes Land Kulturstadt Kein Urlaub Anderes Kulturstadt Berg Kein Urlaub Meer Berg Anderes Meer Kein Urlaub Kulturstadt Wie viele sind das? Was war das beliebteste Ziel? Können wir das in wenigen Sekunden sagen?

Wenn wir alles in eine Tabelle schreiben… Die Daten, die davor nacheinander eingetragen waren, sind jetzt in einer Tabelle zusammengefasst. Insgesamt waren es 50 Schüler. Das bevorzugte Ziel war das Meer! Art des Urlaubs Meer Kein Urlaub Berg Anderes Kulturstadt Land Insgesamt 17 12 7 6 5 3 50

Lasst uns jetzt anfangen! • Bevor wir „lustige“ Sachen mit den Daten machen können, müssen wir die richtigen Bezeichnungen dafür lernen!! • WIR MÜSSEN EIN PAAR BEGRIFFE DER FACHSPRACHE LERNEN Neue Wörter oder „alte“ Wörter mit neuer Bedeutung

MERKMALE UND AUSPRÄGUNGEN MERKMAL oder VARIABLE oder PHÄNOMEN: ist eine interessante Eigenschaft wird erhoben / gemessen / beobachtet AUSPRÄGUNGEN: sind mögliche Werte des Merkmals, sie sind numerisch oder nicht numerisch und müssen: Ø erschöpfend sein: sie müssen alle Wesensarten des betrachteten Merkmals enthalten Ø nicht überschneidend sein: sie sind genau bestimmt oder schließen sich gegenseitig aus. z. B. das von den Lehrern erhobene Merkmal ist die ART DES URLAUBS und die Ausprägungen sind: Kein Urlaub, Meer, Berg, Land, Kulturstadt und anderes

ERHEBUNGSEINHEIT und GRUNDGESAMTHEIT Die ERHEBUNGSEINHEIT ist das Grundelement, an dem die Merkmale beobachtet werden In der Erhebung über die Variable ART DES URLAUBS sind die 50 Schüler die Erhebungseinheiten Es kann „natürlich“ oder konventionell sein z. B. ein Mensch, ein Auto z. B. die Familie Die Erhebungseinheit oder das Grundelement der Erhebung muss immer genau definiert werden. DIE GRUNDGESAMTHEIT ist die Summe aller berücksichtigten Erhebungseinheiten, die in einem oder mehreren Merkmalen übereinstimmen. Mit n wird die Gesamtanzahl der berücksichtigten Erhebungseinheiten bezeichnet.

Und jetzt geht’s mit der Praxis weiter. . .
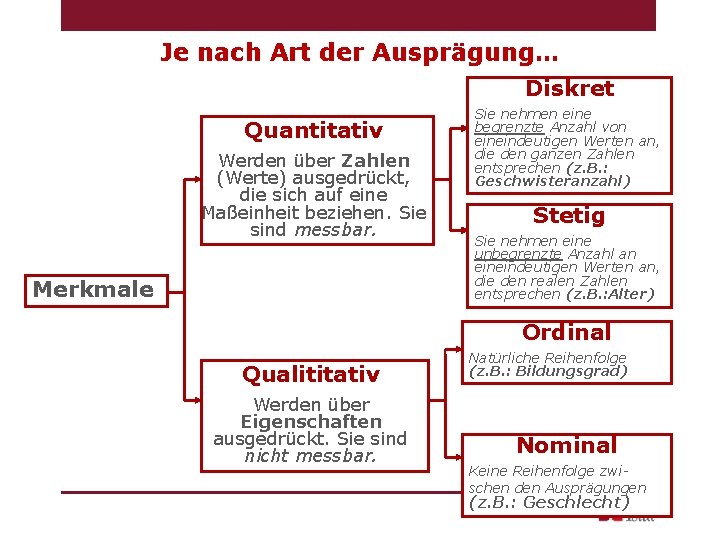
Je nach Art der Ausprägung… Diskret Quantitativ Werden über Zahlen (Werte) ausgedrückt, die sich auf eine Maßeinheit beziehen. Sie sind messbar. Merkmale Sie nehmen eine begrenzte Anzahl von eineindeutigen Werten an, die den ganzen Zahlen entsprechen (z. B. : Geschwisteranzahl) Stetig Sie nehmen eine unbegrenzte Anzahl an eineindeutigen Werten an, die den realen Zahlen entsprechen (z. B. : Alter) Ordinal Qualititativ Werden über Eigenschaften ausgedrückt. Sie sind nicht messbar. Natürliche Reihenfolge (z. B. : Bildungsgrad) Nominal Keine Reihenfolge zwischen den Ausprägungen (z. B. : Geschlecht)

Instrumente der Statistik Mit der Statistik wird eine Menge an Daten einer Erhebung zusammengefasst und in eine Form gebracht, die leicht zu interpretieren ist. Damit wird die Zusammensetzung der Grundgesamtheit in Bezug auf die beobachteten Merkmale hervorgehoben und es werden Hinweise für die weiteren Bearbeitungen entnommen. Über welche Instrumente der Statistik werden wir sprechen? Ø Häufigkeiten Ø Häufigkeitstabellen Ø Einfache charakteristische Konstanten (Lagemaße, Streuungsmaße. . . )

Die Häufigkeiten Die einfachste Messtechnik ist die Zählung, also die Anzahl, wie oft jede Ausprägung eines Merkmals auftritt. Jede Erhebungseinheit - muss klassifiziert werden können erschöpfende Klassen - muss zu einer einzigen Klasse gehören getrennte Klassen Um die Häufigkeiten zu berechnen, benötigt man die einheitliche Verteilung des Merkmals, also die Auflistung der Ausprägungen, die für jede einzelne Erhebungseinheit in der Grundgesamtheit beobachtet wurden Art des Urlaubs Meer Kulturstadt Meer Anderes Kulturstadt Berg Kein Urlaub Anderes Kein Urlaub Meer Ausgehend von den Berg Meer aufgereihten Daten Meer Kein Urlaub zählt man, wie oft jede Kein Urlaub Land Ausprägung. Berg vorkommt Kulturstadt Kein Urlaub und erhält so die Kein Urlaub Meer Häufigkeitstabelle! Meer Kein Urlaub Berg Meer Insgesamt 17 12 Kein Urlaub Meer Berg 7 Kein Urlaub Meer Land Kein Urlaub Anderes Land 6 Anderes Kulturstadt Berg 5 Meer Berg Anderes 3 Meer Kein Urlaub Kulturstadt Anderes Kulturstadt Land Insgesamt 50

Absolute Häufigkeiten Die statistische Tabelle ist eine Übersicht mit zwei Spalten: Ø in der ersten Spalte sind die Ausprägungen (einzeln oder in Klassen zusammengefasst), die das Merkmal annehmen kann, aufgelistet Ø in der zweiten Spalte sind die Häufigkeiten enthalten Der Teil oberhalb der Spalten heißt Tabellenkopf. Tipo di vacanza Ausprägung x 1 mare x 2 nessun viaggio … montagna xj altro … città d'arte xk campagna Insgesamt Totale Absolute Frequenze Häufigkeit assolute 17 n 1 12 n 2 … 7 n 6 j … 5 n 3 k 50 n Die absoluten Häufigkeiten sind die Anzahl, wie oft jede Ausprägung in der beobachteten Grundgesamtheit vorkommt Mit nj werden die Häufigkeiten angegeben und mit xj die Ausprägungen mit dem Index j=1, 2, …, K wobei K die Anzahl der Ausprägungen ist

Relative Häufigkeiten Teilt man die absoluten Häufigkeiten durch n, die Gesamtanzahl der Erhebungseinheiten, erhält man die relativen Häufigkeiten. Art des Urlaubs Meer Kein Urlaub Berg Anderes Kulturstadt Land Insgesamt Absolute Häufigkeit 17 12 7 6 5 3 50 Relative Häufigkeit 0, 34 0, 24 0, 12 0, 10 0, 06 1 Die ABSOLUTEN HÄUFIGKEITEN von zwei Datenverteilungen, auch derselben Art, sind nicht vergleichbar, da sie sich normalerweise auf eine unterschiedliche Gesamtanzahl an Einheiten beziehen.

Wieso werden relative Häufigkeiten berechnet? Da die absoluten Häufigkeiten von n abhängen, haben sie unterschiedliche Bedeutung je nach Gesamtanzahl der Einheiten. Dies ist besonders dann wichtig, wenn Häufigkeitsverteilungen von 2 oder mehr Grundgesamtheiten verglichen werden. Betrachten wir zwei Gruppen, die nach Geschlecht (M Männer und F Frauen) klassifiziert sind. Über die relativen Häufigkeiten können wir erkennen, in welcher Gruppe der Männeranteil höher ist. Gruppe 1 M F Insgesamt Absolute Relative Häufigkeit 2 0, 333 4 0, 667 6 1 Gruppe 2 M F Insgesamt Absolute Häufigkeit 12 46 Relative Häufigkeit 0, 207 0, 793 58 1
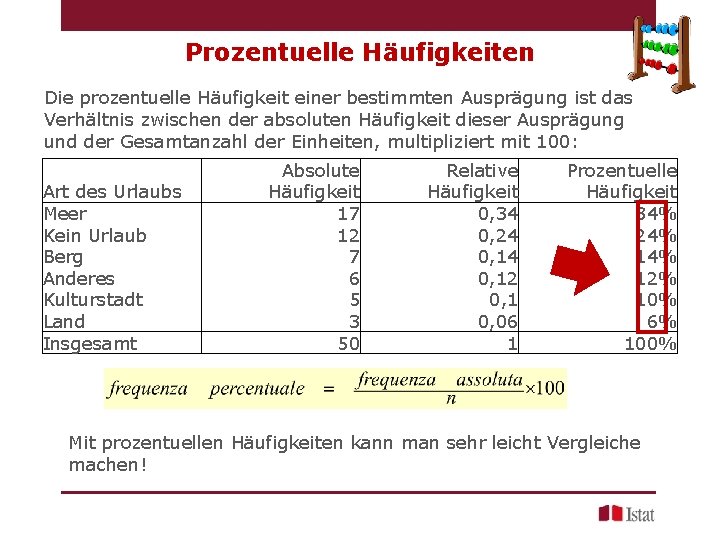
Prozentuelle Häufigkeiten Die prozentuelle Häufigkeit einer bestimmten Ausprägung ist das Verhältnis zwischen der absoluten Häufigkeit dieser Ausprägung und der Gesamtanzahl der Einheiten, multipliziert mit 100: Art des Urlaubs Meer Kein Urlaub Berg Anderes Kulturstadt Land Insgesamt Absolute Häufigkeit 17 12 7 6 5 3 50 Relative Häufigkeit 0, 34 0, 24 0, 12 0, 1 0, 06 1 Prozentuelle Häufigkeit 34% 24% 12% 10% 6% 100% Mit prozentuellen Häufigkeiten kann man sehr leicht Vergleiche machen!

Berechnung der prozentuellen Häufigkeiten! Die Schüler einer Klasse werden mit der qualitativen Variablen HAARFARBE klassifiziert. Hier ist die Häufigkeitstabelle: Haarfarbe (Merkmal) Schwarz Absolute Häufigkeit 10 Braun 6 Rot 1 Blond 5 INSGESAMT Berechnung der prozentuellen Häufigkeiten 22 Haarfarbe Absolute Häufigkeit Prozentuelle Häufigkeit 10 45, 46% Braun 6 27, 27% Rot 1 4, 55% Blond 5 22, 72% 22 100% Schwarz INSGESAMT

Ein Detail zu den AUSPRÄGUNGEN Bei den diskreten Variablen lassen sich die Ausprägungen ziemlich einfach bestimmen, aber bei den STETIGEN Variablen muss man eine DISKRETISIERUNG vornehmen, also KLASSEN der Werte ermitteln, die das Merkmal annimmt, das uns interessiert. GEWICHT (kg) ANZAHL SCHÜLER (Häufigkeit) Darstellung nach Gewichtsklassen GEWICHTSKLASSE ANZAHL SCHÜLER (Häufigkeit) 52 1 54 1 50 – 60 kg 4 55 2 60 – 70 kg 7 61 1 70 – 80 kg 3 63 1 Insgesamt 14 68 2 69 3 71 1 73 1 75 1 INSGESAMT 14

Einige Informationen zu den KLASSEN Bei der KLASSIFIKATION müssen bestimmte Regeln eingehalten werden Ø die Anzahl der Klassen muss ausgewogen sein weder zu viele, noch zu wenige Ø die Klassen müssen normalerweise gleich groß sein Ø offene Klassen sind möglichst zu vermeiden Die Informationen werden in einer Verteilung nach Klassen ungenauer, aber die Darstellung der Verteilung wird einfacher und schneller.

LAGEMASSE Um eine Verteilung mit einem einzigen Wert zusammenzufassen, kann ein Lagemaß verwendet werden. Diese Maße informieren über die Größenordnung, die das Merkmal in der Grundgesamtheit aufweist. Die bekanntesten sind der arithmetische Mittelwert, der Modus und der Median, aber es gibt noch viele andere. Jedes hat seine Eigenheiten…. z. B. Welches ist die durchschnittliche Farbe eurer Haare? Achtung: Nicht alle Merkmale sind gleich und wir müssen deshalb unterschiedlich handeln… (erinnert ihr euch an die qualitativen und quantitativen Merkmale? ? )

MODUS Der MODUS einer Datenverteilung bezeichnet die GRÖSSTE HÄUFIGKEIT. Es handelt sich im Grunde genommen um den häufigsten Begriff. In dieser Tabelle sind die 19 Schüler nach dem Merkmal NOTE klassifiziert. Der Modus ist die häufigste Ausprägung: das ist die Note 6! NOTE Absolute Häufigkeit 5 4 6 8 7 4 8 2 9 1 Insgesamt 19 Er kann für jede Art von Merkmale ermittelt werden, auch für qualitative nominale.

MEDIAN Der MEDIAN ist der Wert, welcher an der MITTLEREN STELLE einer Verteilung von Daten steht, die aufsteigend geordnet sind. In dieser Tabelle sind die 19 Schüler nach dem Merkmal NOTE klassifiziert. Um den Median festzustellen, werden alle Daten aufsteigend angeordnet. Dann wird der ZENTRALE WERT festgestellt: Das ist der Wert in der Mitte, bei dem auf der rechten und NOTE Absolute linken Seite gleich viele Werte stehen. Häufigkeit 5 4 6 8 7 4 8 2 9 1 Insgesamt 19 555566666 6667777889 Wenn es sich um eine gerade Anzahl von Daten handelt, gibt es zwei Werte, die genau in der Mitte stehen. Der Median ist der arithmetische Mittelwert dieser zwei Werte.

ARITHMETISCHER MITTELWERT Der MITTELWERT ist ein analytischer Mittelwert und kann also nur für QUANTITATIVE Merkmale berechnet werden. Man berechnet ihn, indem man alle beobachteten Werte addiert und durch die Gesamtanzahl der Erhebungseinheiten dividiert. Im vorigen Beispiel 55556666 6 6667777889 Es scheint unlogisch, dass eine Dezimalzahl die Zusammen-fassung von diskreten Daten ist. Das lässt sich aber damit erklären, dass der Mittelwert ein stellvertretender Wert für alle beobachteten Werte ist und sich nicht auf eine einzelne Maßeinheit bezieht!

ARITHMETISCHER MITTELWERT Wenn die Daten in einer Tabelle dargestellt werden, ändert sich die Formel. Jeder beobachtete Wert wird mit der jeweiligen absoluten Häufigkeit gewichtet und alles durch n dividiert. NOTE xj 5 6 7 8 9 Insgesamt Absolute Häufigkeit nj xj x n j 4 8 4 2 1 19 20 48 28 16 9 121

STREUUNG Der MITTELWERT REICHT NICHT, um ein Bild von der Verteilung eines Merkmals darzustellen! Man braucht Indikatoren, die VERSCHIEDENHEIT der beobachteten Einheiten, also ihre HETEROGENITÄT, beschreiben. z. B. zwei Verteilungen mit dem gleichen arithmetischen Mittelwert, die sich aber sehr voneinander unterscheiden Diese Indikatoren sind die STREUUNGSMASSE. Die STREUUNG einer Verteilung ist die Tendenz der Einheiten, verschiedene Ausprägungen des Merkmals anzunehmen.
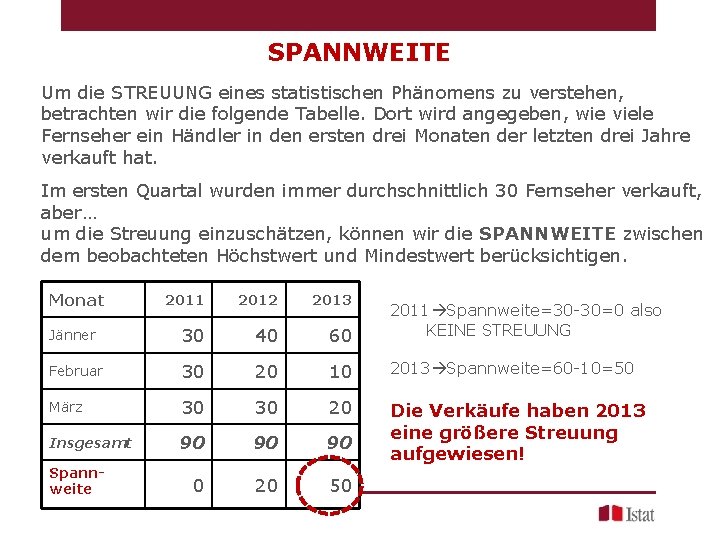
SPANNWEITE Um die STREUUNG eines statistischen Phänomens zu verstehen, betrachten wir die folgende Tabelle. Dort wird angegeben, wie viele Fernseher ein Händler in den ersten drei Monaten der letzten drei Jahre verkauft hat. Im ersten Quartal wurden immer durchschnittlich 30 Fernseher verkauft, aber… um die Streuung einzuschätzen, können wir die SPANNWEITE zwischen dem beobachteten Höchstwert und Mindestwert berücksichtigen. Monat 2011 2012 2013 Jänner 30 40 60 2011 Spannweite=30 -30=0 also KEINE STREUUNG Februar 30 20 10 2013 Spannweite=60 -10=50 März 30 30 20 Insgesamt 90 90 90 Die Verkäufe haben 2013 eine größere Streuung aufgewiesen! 0 20 50 Spannweite

…und jetzt… Gute Arbeit! Übersetzung: / Tradotto da: Rete per la promozione della cultura statistica
- Slides: 28