Berry Phase Effects on Bloch Electrons in Electromagnetic

Berry Phase Effects on Bloch Electrons in Electromagnetic Fields Qian Niu 牛� University of Texas at Austin 北京大学 Collaborators: Y. Gao, Shengyuan Yang, C. P. Chuu, D. Xiao, W. Yao, D. Culcer, J. R. Shi, Y. G. Yao, G. Sundaram, M. C. Chang, T. Jungwirth, J. Sinova, A. H. Mac. Donald H. Weitering, J. Beach, M. Tsoi, J. Erskine Supported by : DOE, NSF, Welch Foundation

Outline • Berry phase and its applications • Berry curvature in momentum space – Anomalous velocity, Anomalous Hall effect – Density of States, Orbital Magnetization – Effective Quantum Mechanics • Second order extension – Positional shift – Magnetoelectric Polarization – Nonlinear anomalous Hall effect

Berry Phase In the adiabatic limit: Geometric phase:

Well defined for a closed path Stokes theorem Berry Curvature

Analogy to Gauge Field Berry curvature Magnetic field Berry connection Vector potential Geometric phase Aharonov-Bohm phase Chern number Dirac monopole

Analogy to Riemann Geometry Berry curvature Gaussian curvature Berry connection Levi-Civita connection Geometric phase Holonomy angle Chern number Genus

Applications • Berry phase interference, energy levels, polarization in crystals • Berry curvature spin dynamics, electron dynamics in Bloch bands • Chern number quantum Hall effect, quantum charge pump ``Berry Phase Effects on Electronic Properties”, by D. Xiao, M. C. Chang, Q. Niu, Review of Modern Physics

Outline • Berry phase and its applications • Berry curvature in momentum space – Anomalous velocity, Anomalous Hall effect – Density of States, Orbital Magnetization – Effective Quantum Mechanics • Second order extension – Positional shift – Magnetoelectric Polarization – Nonlinear anomalous Hall effect

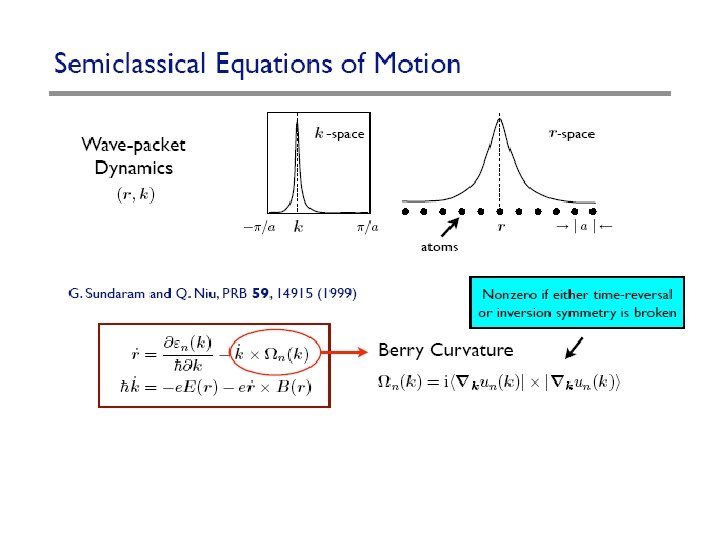
Symmetry properties • time reversal: • space inversion: • both: • violation: ferromagnets, asymmetric crystals

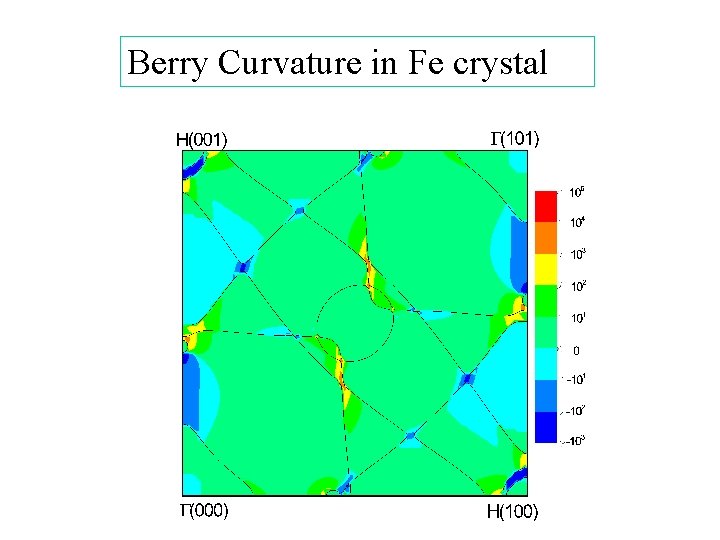
Berry Curvature in Fe crystal

Anomalous Hall effect • velocity • distribution g( ) = f( ) + df( ) • current Intrinsic

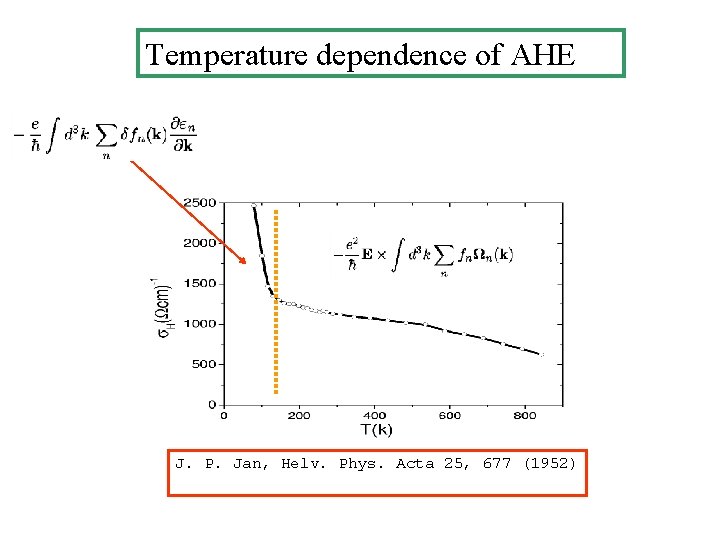
Temperature dependence of AHE J. P. Jan, Helv. Phys. Acta 25, 677 (1952)

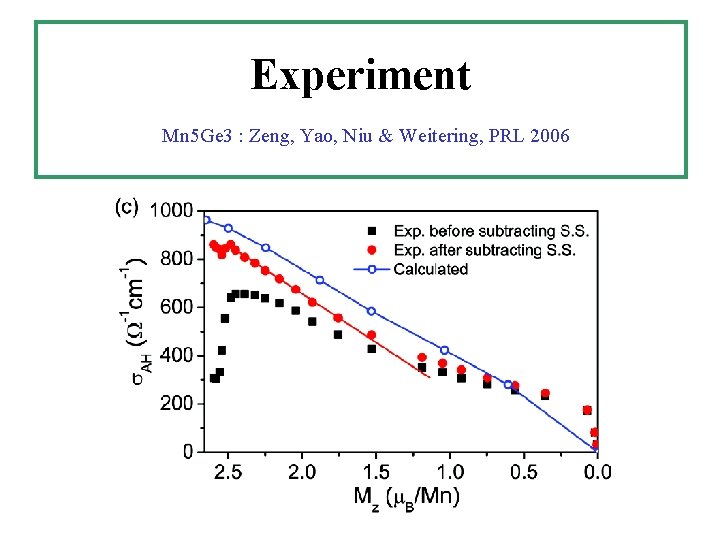
Experiment Mn 5 Ge 3 : Zeng, Yao, Niu & Weitering, PRL 2006

Intrinsic AHE in other ferromagnets • Semiconductors, Mnx. Ga 1 -x. As – Jungwirth, Niu, Mac. Donald , PRL (2002) , J Shi’s group (2008) • Oxides, Sr. Ru. O 3 – Fang et al, Science , (2003). • Transition metals, Fe – Yao et al, PRL (2004), Wang et al, PRB (2006), X. F. Jin’s group (2008) • Spinel, Cu. Cr 2 Se 4 -x. Brx – Lee et al, Science, (2004) • First-Principle Calculations-Review – Gradhand et al (2012)

Some Magneto Effects Density of states and specific heat: Magnetoconductivity:

Orbital magnetization Free energy Xiao, Shi & Niu, PRL 2005 Xiao, et al, PRL 2006 Also see: Thonhauser et al, PRL (2005). Ceresoli et al PRB (2006).

Anomalous Thermoelectric Transport • Berry phase correction • Thermoelectric transport

Thermal Hall Conductivity Phonon Magnon Electron Wiedemann-Franz Law

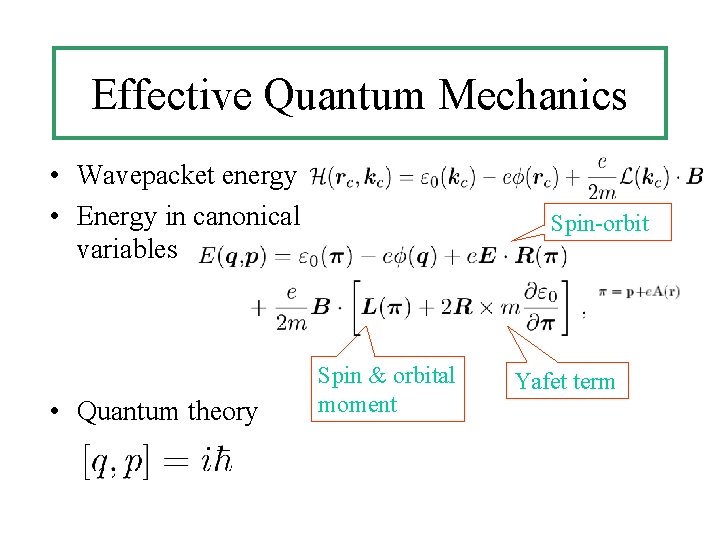
Effective Quantum Mechanics • Wavepacket energy • Energy in canonical variables • Quantum theory Spin-orbit Spin & orbital moment Yafet term

Outline • Berry phase and its applications • Berry curvature in momentum space – Anomalous velocity, Anomalous Hall effect – Density of States, Orbital magnetization – Effective Quantum Mechanics • Second order extension – Positional Shift – Magnetoelectric Polarization – Nonlinear anomalous Hall effect

Why second order? • In many systems, first order response vanishes • May be interested in magnetic susceptibility, electric polarizebility, magneto-electric coupling • Magnetoresistivity • Nonlinear anomalous Hall effects

Positional Shift • Use perturbed band: • Solve from the first order energy correction: • Modification of the Berry connection – the positional shift

Equations of Motion • Effective Lagrangian: • Equations of motion

Magnetoelectric Polarization • Polarization in solids: • Correction under electromagnetic fields: • Magnetoelectric Polarization:

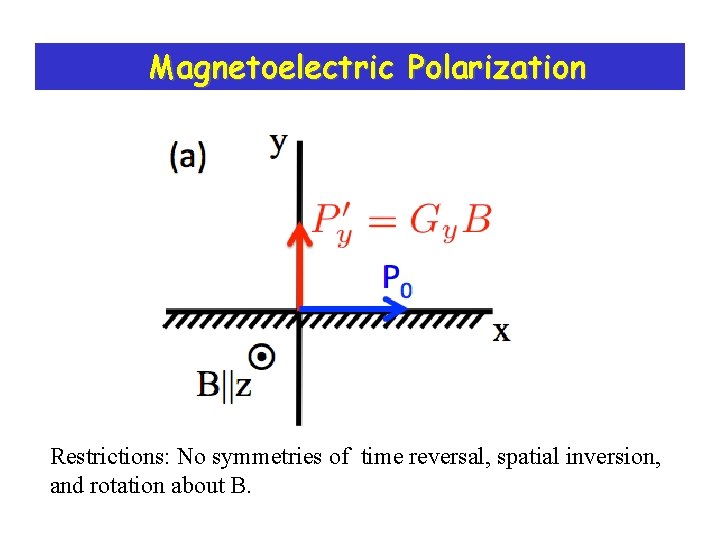
Magnetoelectric Polarization Restrictions: No symmetries of time reversal, spatial inversion, and rotation about B.

Nonlinear anomalous Hall current • Intrinsic current: • Results – only anomalous Hall current:

Electric-field-induced Hall Effect • Electric field induced Hall conductivity (2 -band model):

Magnetic-field induced anomalous Hall • Model Hamiltonian: • Magnetic field induced Hall conductivity: • Compare to ordinary Hall effect

Conclusion • Berry phase is a unifying concept • Berry curvature in momentum space – Anomalous velocities, Anomalous Hall effect – Density of states, Orbital magnetization – Effective quantum Mechanics • Second order extension • • • Positional shift Magnetoelectric polarization Nonlinear anomalous Hall effect