Berry Phase and Anomalous Hall Effect Qian Niu

Berry Phase and Anomalous Hall Effect Qian Niu University of Texas at Austin Supported by DOE-NSET NSF-Focused Research Group NSF-PHY Welch Foundation International Center of Quantum Structures

Outline • • Berry phase—an introduction Semiclassical transport Anomalous Hall effect Summary

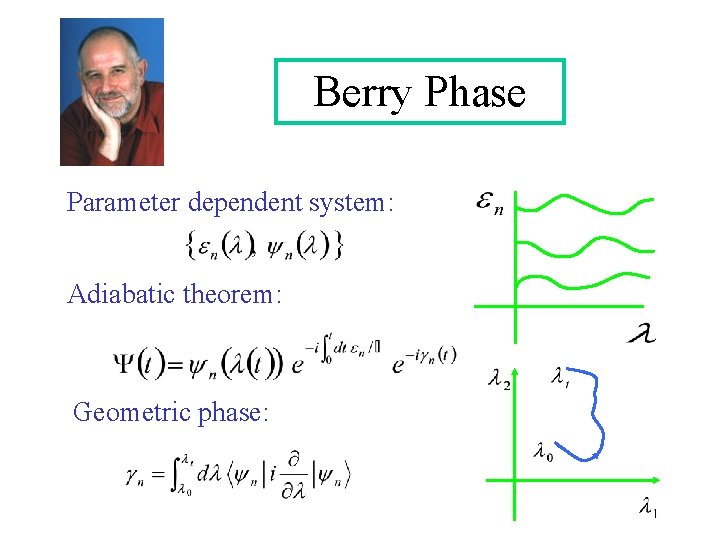
Berry Phase Parameter dependent system: Adiabatic theorem: Geometric phase:

Well defined for a closed path Stokes theorem Berry Curvature

Analogies Berry curvature Magnetic field Berry connection Vector potential Geometric phase Aharonov-Bohm phase Chern number Dirac monopole

Applications • Berry phase interference, energy levels, polarization in crystals • Berry curvature spin dynamics, electron dynamics in Bloch bands • Chern number quantum Hall effect, quantum charge pump

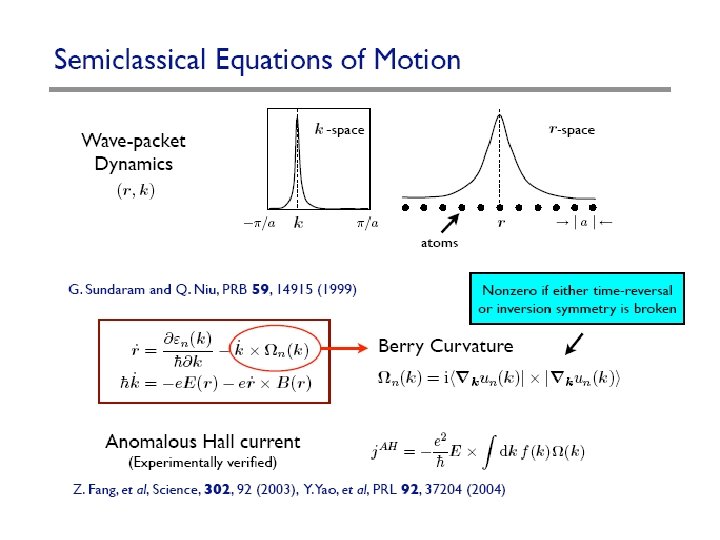
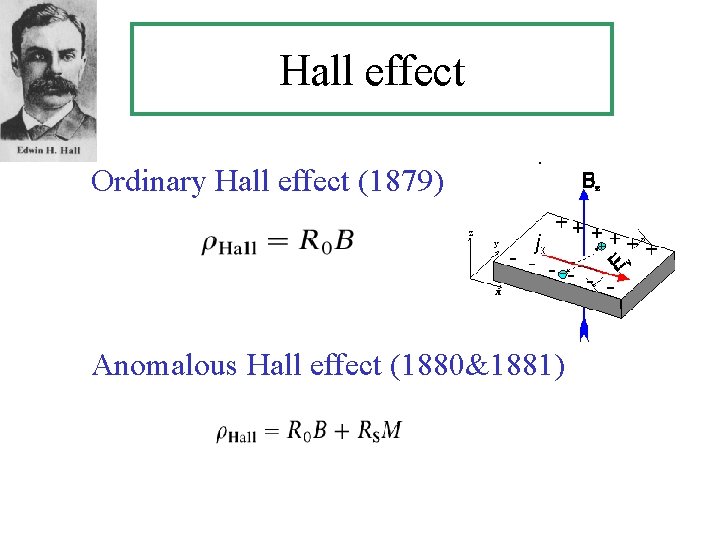
Hall effect Ordinary Hall effect (1879) Anomalous Hall effect (1880&1881)

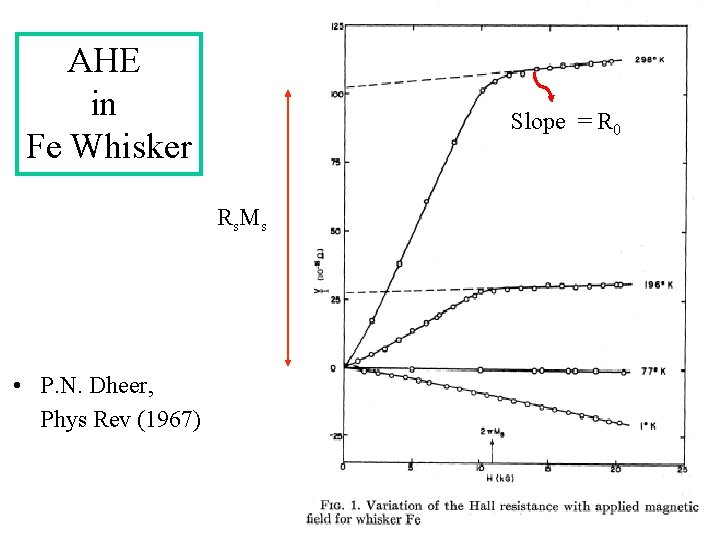
AHE in Fe Whisker Slope = R 0 R s. M s • P. N. Dheer, Phys Rev (1967)

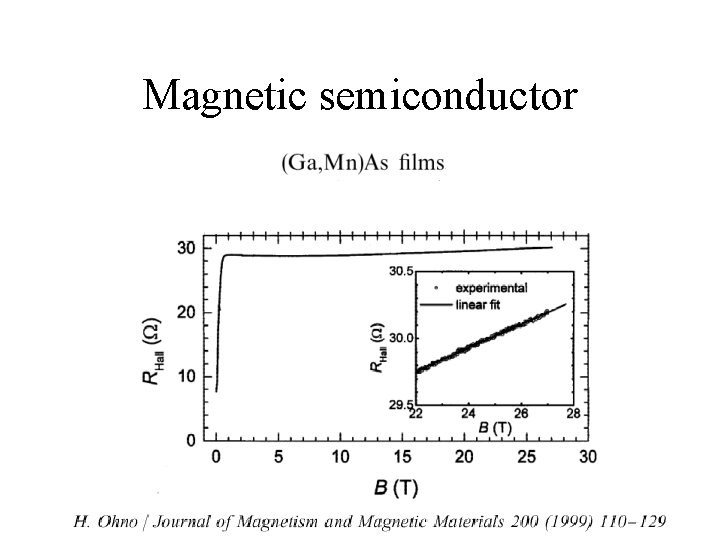
Magnetic semiconductor

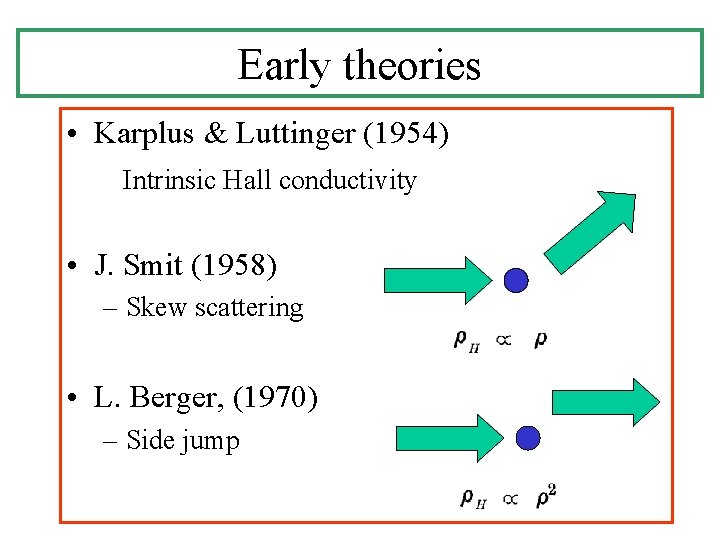
Early theories • Karplus & Luttinger (1954) Intrinsic Hall conductivity • J. Smit (1958) – Skew scattering • L. Berger, (1970) – Side jump

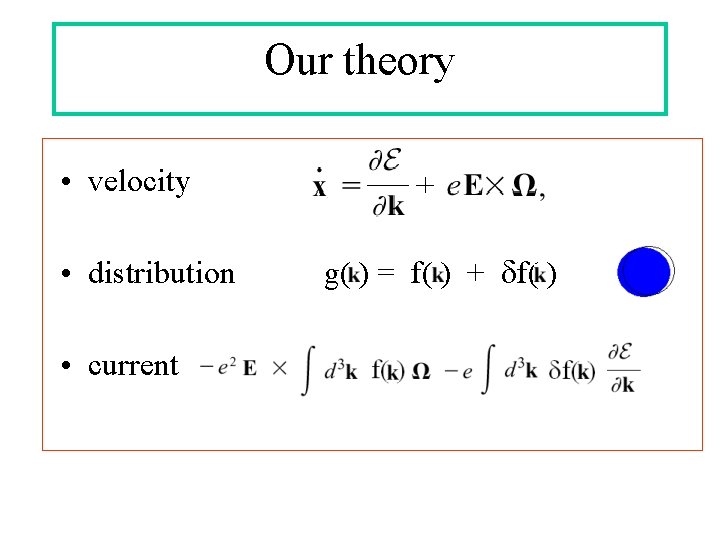
Our theory • velocity • distribution • current g( ) = f( ) + df( )

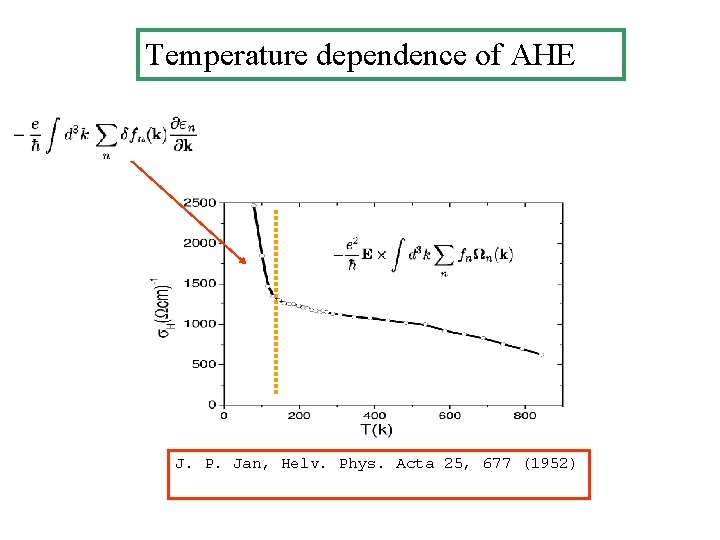
Temperature dependence of AHE J. P. Jan, Helv. Phys. Acta 25, 677 (1952)

Ferromagnetic bcc Fe Yugui. Yao et al: Phys. Rev. Lett. 92, 037204 (2004) Wien 2000: LAPW spin density functional generalized gradient approximation spin-orbit coupling included in the APW sphere.

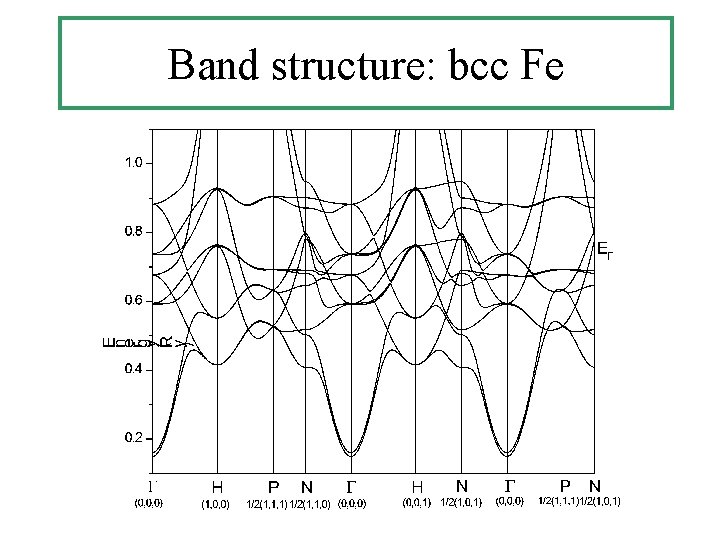
Band structure: bcc Fe

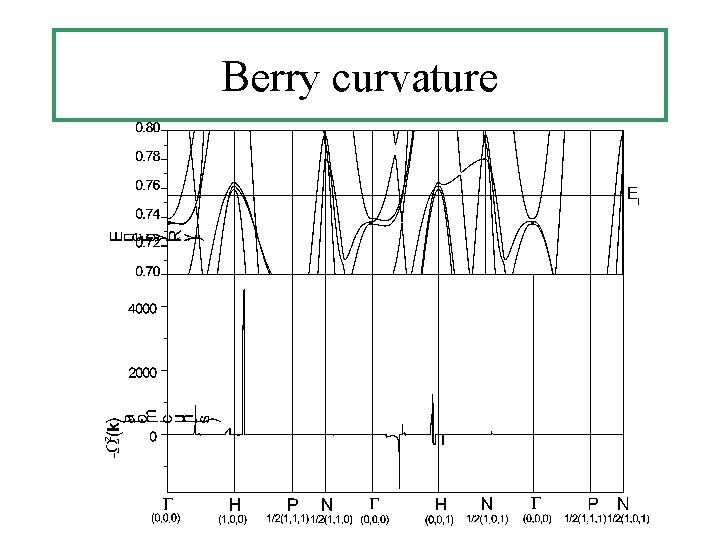
Berry curvature

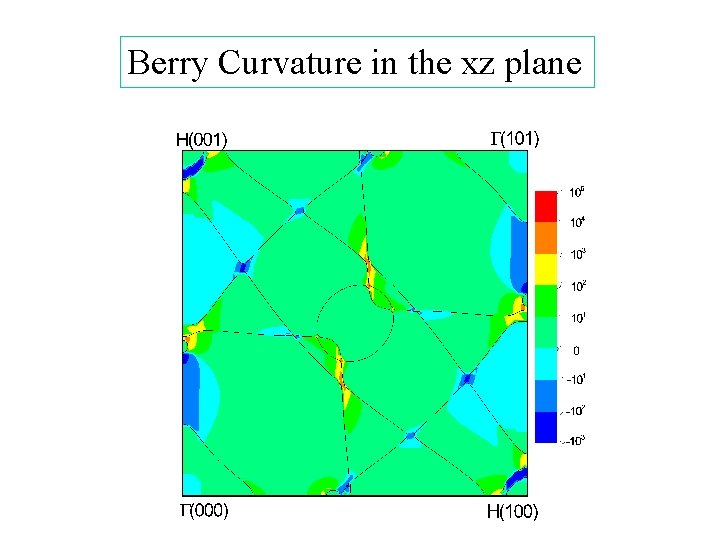
Berry Curvature in the xz plane

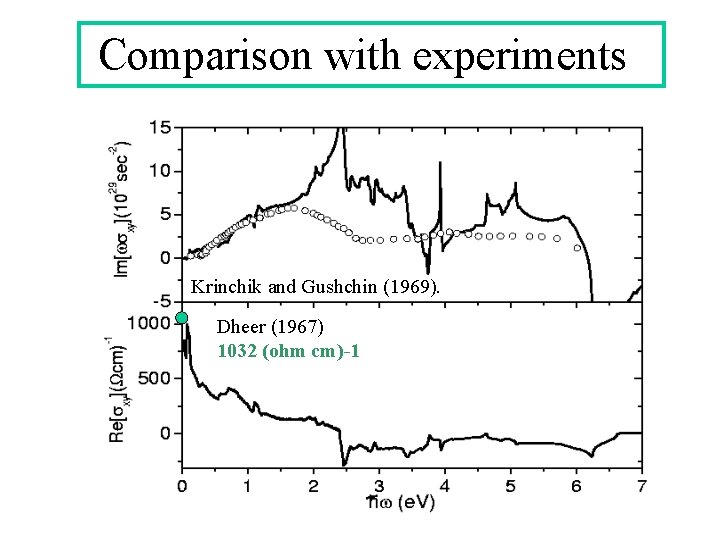
Comparison with experiments Krinchik and Gushchin (1969). Dheer (1967) 1032 (ohm cm)-1

Kubo formula

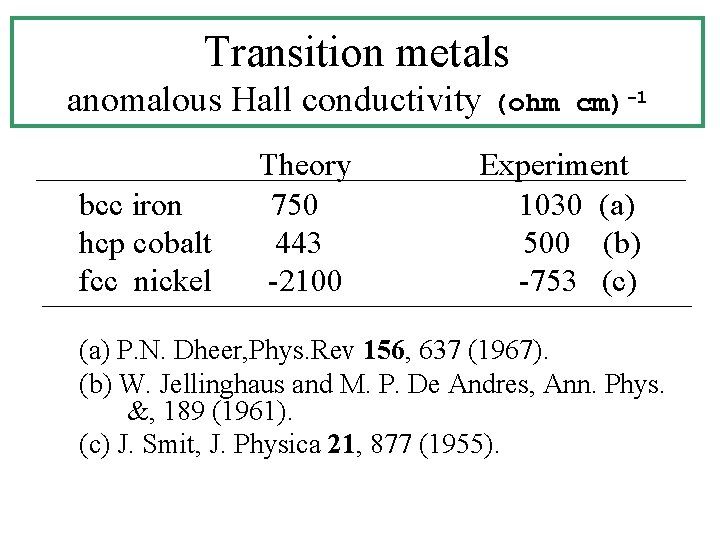
Transition metals anomalous Hall conductivity (ohm bcc iron hcp cobalt fcc nickel Theory 750 443 -2100 cm)-1 Experiment 1030 (a) 500 (b) -753 (c) (a) P. N. Dheer, Phys. Rev 156, 637 (1967). (b) W. Jellinghaus and M. P. De Andres, Ann. Phys. &, 189 (1961). (c) J. Smit, J. Physica 21, 877 (1955).

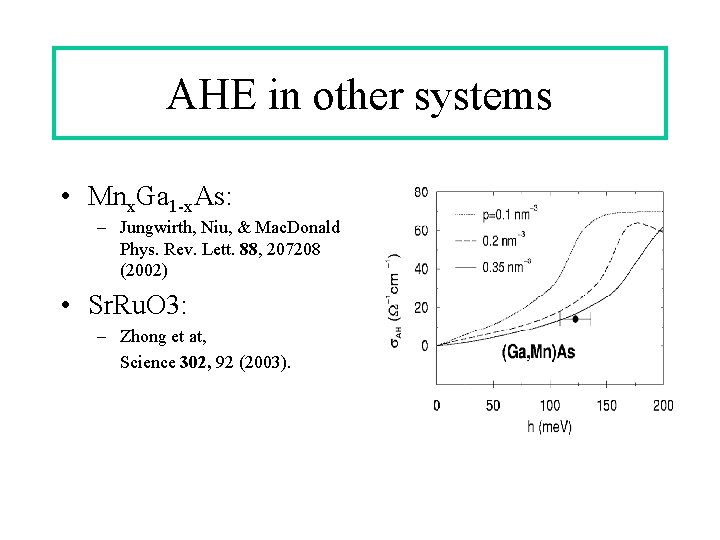
AHE in other systems • Mnx. Ga 1 -x. As: – Jungwirth, Niu, & Mac. Donald Phys. Rev. Lett. 88, 207208 (2002) • Sr. Ru. O 3: – Zhong et at, Science 302, 92 (2003).

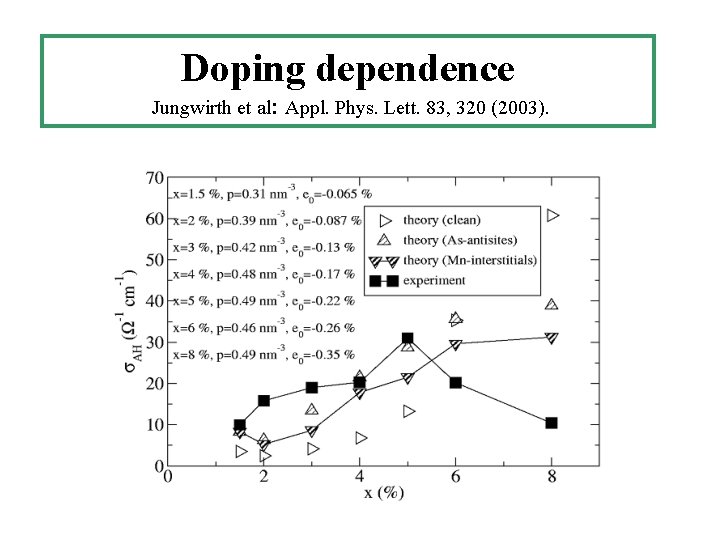
Doping dependence Jungwirth et al: Appl. Phys. Lett. 83, 320 (2003).

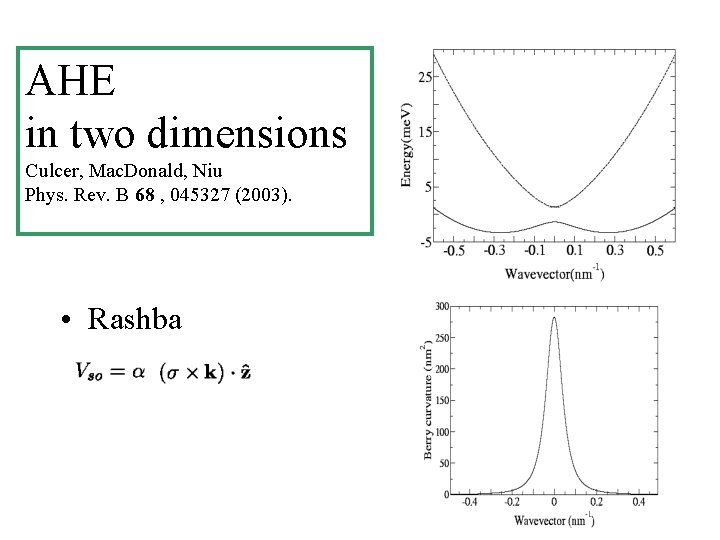
AHE in two dimensions Culcer, Mac. Donald, Niu Phys. Rev. B 68 , 045327 (2003). • Rashba

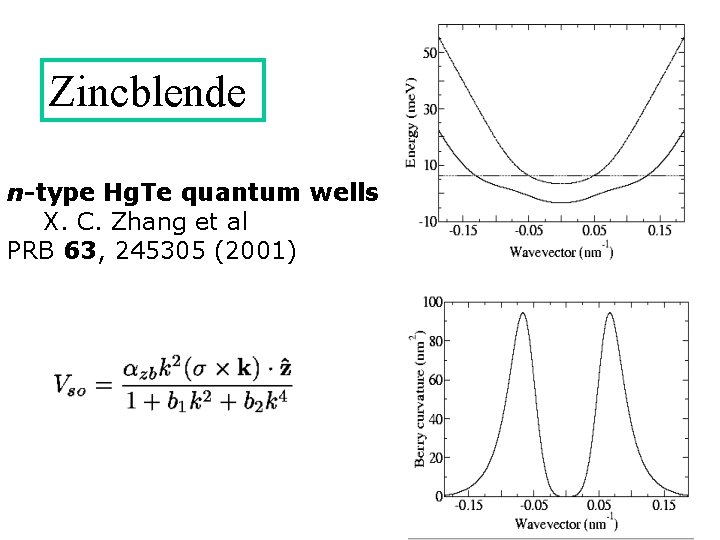
Zincblende n-type Hg. Te quantum wells X. C. Zhang et al PRB 63, 245305 (2001)

Summary Berry phase A unifying concept with many applications Bloch electron dynamics in weak fields Berry phase around the Brillouin zone: ------Polarization Berry curvature: a ‘magnetic field’ in the k space. -----Anomalous Hall effect Phase space density of states is modified. -----Orbital magnetization, etc.