Bernoullis Equation Mechanical Energy Balance Flow Measurements 1

• Bernoulli’s Equation (Mechanical Energy Balance) • Flow Measurements 1

Mechanical Energy Balance From the energy equation, dividing by mass and assuming incompressible flow, then rearranging Let’s define the friction heating per unit mass: 2

Mechanical Energy Balance This is the Mechanical Energy Balance or Bernoulli’s equation By dividing above equation with g we obtain the “head form” of the Mechanical Energy Balance: Ø F/g (sometimes symbolized as h. L) is the friction or head loss 3

Simplifications Assumptions: – Steady, incompressible, frictionless (inviscide) flow – No heat transfer or change in internal energy, no shaft work – Single input-output Bernoulli’s equation may reduced to: In terms of “heads” (units of length) 4

Bernoulli’s Equation - Restrictions • Applicable to large number of practical engineering problems though with several limitations. – – Simple form of equation only valid for incompressible fluids. No account taken of any mechanical devices in system which add/remove energy (e. g. pumps, turbines, etc. ). No account taken of heat transfer into or out of fluid. No account taken of energy lost due to friction. -Total energy of any stream line is constant. -Link between the flow of the velocity and Pressure. -If the Velocity increase, Pressure decrease. 5

Applications of the Bernoulli Theorem 1/5 Flow and the streamline under consideration are • shown in Fig. 5. 4. Using the Bernoulli equation, we can form a relation between point (1) and point (2) as p 1 + ½ V 12 + gz 1 = p 2 + ½ V 22 + g z 2 § 6

Applications of the Bernoulli Theorem 2/5 At point (1), the pressure is atmospheric (p 1 = po), or the gage pressure is zero, and the fluid is almost at rest (V 1 = 0). At point (2), the exit pressure is also atmospheric (p 2 = po), and the fluid moves at a velocity V. By using point (2) as the datum where z 2 = 0 and the elevation of point (1) is h, the above relation can be reduced to p 0 + ½ (0)2 + gh = p 0 + ½ V 2 + g (0) gh = ½ V 2 Hence we can formulate the velocity V to be V 2 = 2 gh 7

Applications of the Bernoulli Theorem 3/5 • Notice that we can also obtain the similar relation by using the relation between point (3) and point (4). • The pressure and the velocity V 2 for point (4) is similar to point (2). However, the pressure for point (3) is the hydrostatic pressure, i. e. • p 3 = p 0 + g (h - ) and the velocity V 3 is also zero due to an assumption of a large tank. Hence, the relation becomes [ p 0 + g (h - )] + ½ (0)2 + g = p 0 + ½ V 2 + g (0) and thus: V 2 = 2 gh gh = ½ V 2 Hence, between 1 & 5 we can formulate the velocity V to be p 1 + ½ V 12 + gz 1 = p 5 + ½ V 5 2 +g z 5 p 0 + ½ (0)2 + g(h+H) = p 0 + ½ V 52 V 5 = 2 g ( h + H ) (h + H) is vertical distance from point 1 to 5 8

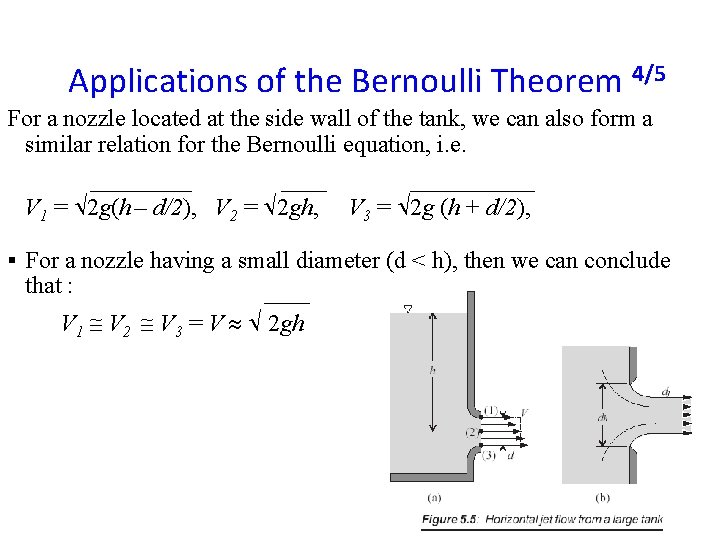
Applications of the Bernoulli Theorem 4/5 For a nozzle located at the side wall of the tank, we can also form a similar relation for the Bernoulli equation, i. e. V 1 = 2 g(h – d/2), V 2 = 2 gh, V 3 = 2 g (h + d/2), § For a nozzle having a small diameter (d < h), then we can conclude that : V 1 V 2 V 3 = V 2 gh 9

Applications of the Bernoulli Theorem 5/5 i. e. , the velocity V is only dependent on the depth of the centre of the nozzle from the free surface h. If the edge of the nozzle is sharp, as illustrated in Fig. 5. 5 b, flow contraction will be occurred to the flow. This phenomenon is known as vena contracta, which is a result of the inability for the fluid to turn at the sharp corner 90°. This effect causes losses to the flow. 10

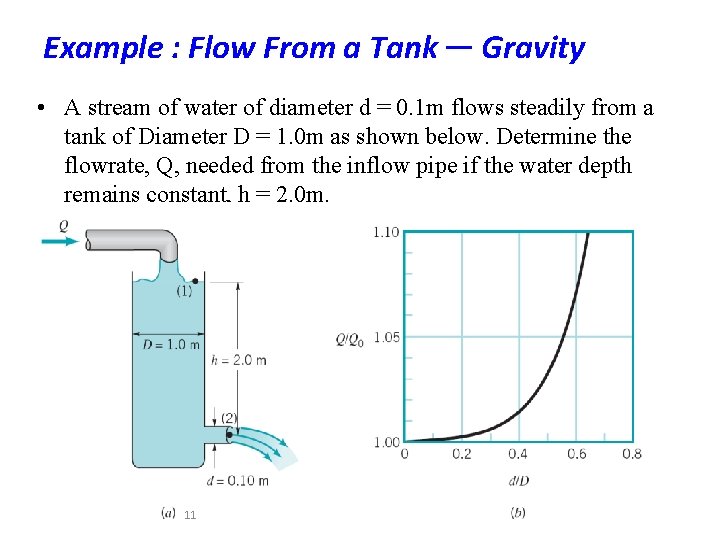
Example : Flow From a Tank－ Gravity • A stream of water of diameter d = 0. 1 m flows steadily from a tank of Diameter D = 1. 0 m as shown below. Determine the flowrate, Q, needed from the inflow pipe if the water depth remains constant, h = 2. 0 m. 11

Solution 1/3 For steady, inviscid, incompressible flow, the Bernoulli equation applied between points (1) and (2) is (1) With the assumptions that p 1 = p 2 = 0, z 1 = h, and z 2 = 0, Eq. 1 becomes (2) Although the water level remains constant (h = constant), there is an average velocity, V 1, across section (1) because of the flow from tank. For the steady incompressible flow, conservation of mass requires Q 1 = Q 2, where Q = AV. Thus, A 1 V 1 =A 2 V 2 , or 12

Solution 2/3 Hence, (3) Equation 1 and 3 can be combined to give Thus, 13

Solution 3/3 In this example we have not neglected the kinetic energy of the water in the tank (V 1≠ 0). If the tank diameter is large compared to the jet diameter (D >> d), Eq. 3 indicates that V 1 << V 2 and the assumption that V 1≒ 0 would be reasonable. The error associated with this assumption can be seen by calculating the ratio of the flowrate assuming V 1 ≠ 0, denoted Q, to that assuming V 1 = 0, denoted Q 0. This ratio, written as is plotted in Fig. E 3. 7 b. With 0 < d/D < 0. 4 it follows that 1 < Q/Q 0 <~ 1. 01, and the Error is assuming V 1 = 0 is less than 1%. Thus, it is often reasonable to assume V 1 = 0. 14

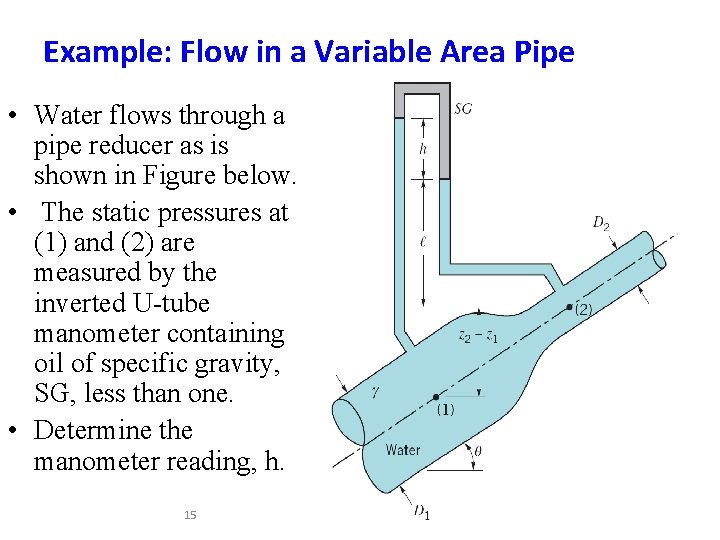
Example: Flow in a Variable Area Pipe • Water flows through a pipe reducer as is shown in Figure below. • The static pressures at (1) and (2) are measured by the inverted U-tube manometer containing oil of specific gravity, SG, less than one. • Determine the manometer reading, h. 15

Solution 1/3 With the assumptions of steady, inviscid, incompressible flow, the Bernoulli equation can be written as The continuity equation provides a second relationship between V 1 and V 2 if we assume the velocity profiles are uniform at those two locations and the fluid incompressible: By combining these two equations we obtain …. (1) 16

Solution 2/3 This pressure difference is measured by the manometer and can be determine by using the pressure-depth ideas. Thus, or …. . (2) Equations 1 and 2 can be combined to give the desired result as follows: or since V 2=Q/A 2 (Ans) 17

Solution 3/3 The difference in elevation, z 1 -z 2, was not needed because the change in elevation term in the Bernoulli equation exactly cancels the elevation term in the manometer equation. However, the pressure difference, p 1 -p 2, depends on the angle θ, because of the elevation, z 1 -z 2, in Eq. 1. Thus, for a given flowrate, the pressure difference, p 1 -p 2, as measured by a pressure gage would vary with θ, but the manometer reading, h, would be independent of θ 18

Applications: Flow Measurement The Bernoulli equation can be applied to several commonly occurring situations in which useful relations involving pressures, velocities and elevations may be obtained. A very important application in engineering is : fluid flow measurement Ø Measurement of velocity : Pitot-static tube Ø Measurement of flow rate: 1 -Venturi meter, 2 - Orifice meter & 19 3 - Rotameter

Flow Measuring Devices Pitot Tube • This is an open-ended tube, bent through 90 o with the nose facing the direction of the oncoming flow. • The fluid is brought to rest at the nose so it measures the fluid’s stagnation or total pressure (po). 20

Stagnation Conditions • Fluid on streamline OX forced to zero velocity at X – this is a stagnation point. • The term stagnation is often used to describe the total pressure conditions as this corresponds to when the dynamic pressure term is zero. • The static pressure at zero-velocity conditions thus relates to 21 the total or stagnation pressure.

Flow Measuring Devices Pitot-Static Tube • Comprises pitot tube surrounded by concentric outer tube with a ring of small holes, carefully positioned to give representative static pressure reading. 22

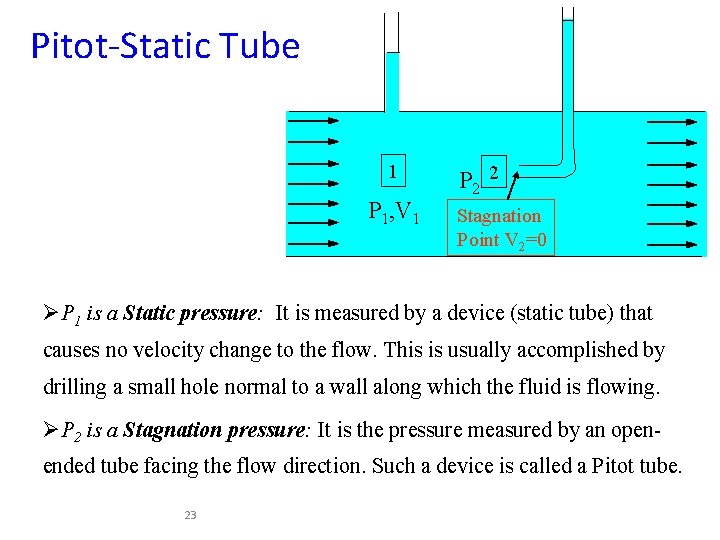
Pitot-Static Tube 1 P 1, V 1 P 2 2 Stagnation Point V 2=0 ØP 1 is a Static pressure: It is measured by a device (static tube) that causes no velocity change to the flow. This is usually accomplished by drilling a small hole normal to a wall along which the fluid is flowing. ØP 2 is a Stagnation pressure: It is the pressure measured by an openended tube facing the flow direction. Such a device is called a Pitot tube. 23

Pitot-Static tube Bernoulli equation between 1 and 2: v. Stagnation Pressure is higher than Static Pressure (Recall that position 2 is a stagnation point: V 2= 0) We can measure pressures P 1 and P 2 using hydrostatics: P 1=Patm + ρgh 1, P 2=Patm + ρgh 2 or using a Pressure Gauge, see next slide 24

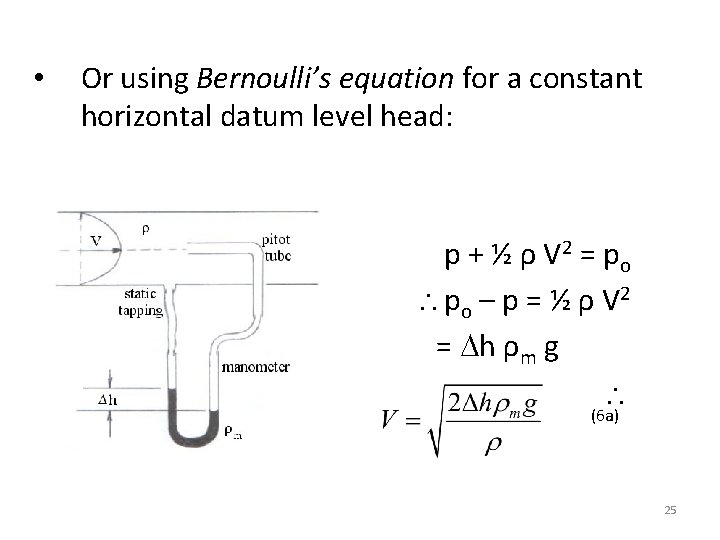
• Or using Bernoulli’s equation for a constant horizontal datum level head: p + ½ ρ V 2 = po – p = ½ ρ V 2 = h ρm g (6 a) 25

Venturi meters, Orifice and Nozzle Basic principle: Increase in velocity causes a decrease in pressure • Fluid is accelerated by forcing it to flow through a constriction, thereby increasing kinetic energy and decreasing pressure energy. • The flow rate is determined by measuring the pressure difference between the meter inlet and a point of reduced pressure. • Desirable characteristics of flow meters: v. Reliable, repeatable calibration v. Introduction of small energy loss into the system v. Inexpensive v. Minimum space requirements 26

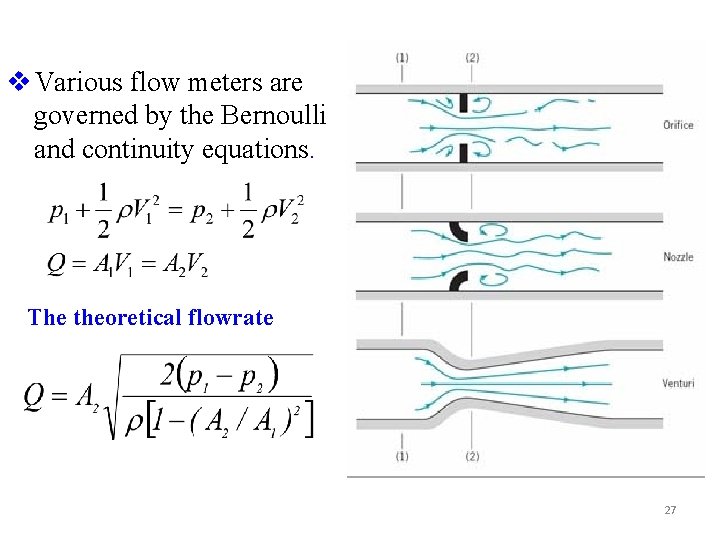
v Various flow meters are governed by the Bernoulli and continuity equations. The theoretical flowrate 27

Flow Measuring Devices Venturi Meter This device consists of a conical contraction, a short cylindrical throat and a conical expansion. The fluid is accelerated by being passed through the converging cone. The velocity at the “throat” is assumed to be constant and an average velocity is used. The venturi tube is a reliable flow measuring device that causes little pressure drop. It is used widely particularly for large liquid and gas flows. P 1 P 2 Where the discharge coefficient, Cd =f(Re), can be found in Figure shown later 28

Flow Measuring Devices Venturi Meter Ignoring friction losses and applying Bernoulli’s equation from (1) to (2). p 1 + ½ ρ V 1 2 = p 2 + ½ ρ V 2 2 Assuming incompressible flow (ρ = constant): p 1 - p 2 = ½ ρ (V 22 - V 12) _______ (eq. 1) Applying continuity equation from (1) to (2): V 2 = (A 1 / A 2) V 1 ______ (eq. 2) 29

Flow Measuring Devices Venturi Meter (Cont. ) Substituting (eq. 2) into (eq. 1): p 1 - p 2 = ½ ρ [(A 1/A 2)2 V 12 – V 12] Rearranging: And (6 b) (6 c) Discharge coefficient (Cd) typically 0. 97. 30

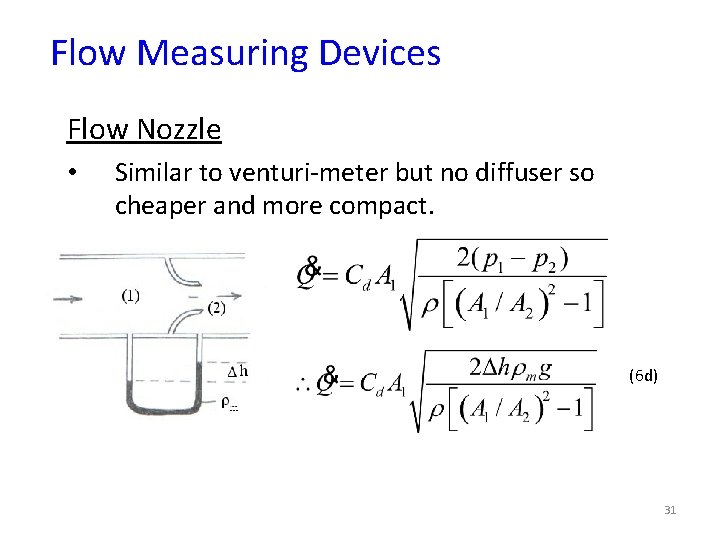
Flow Measuring Devices Flow Nozzle • Similar to venturi-meter but no diffuser so cheaper and more compact. (6 d) 31

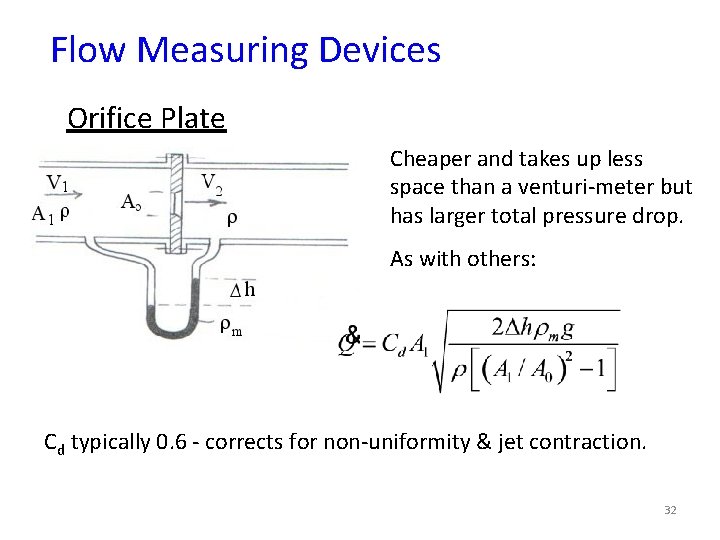
Flow Measuring Devices Orifice Plate Cheaper and takes up less space than a venturi-meter but has larger total pressure drop. As with others: Cd typically 0. 6 - corrects for non-uniformity & jet contraction. 32

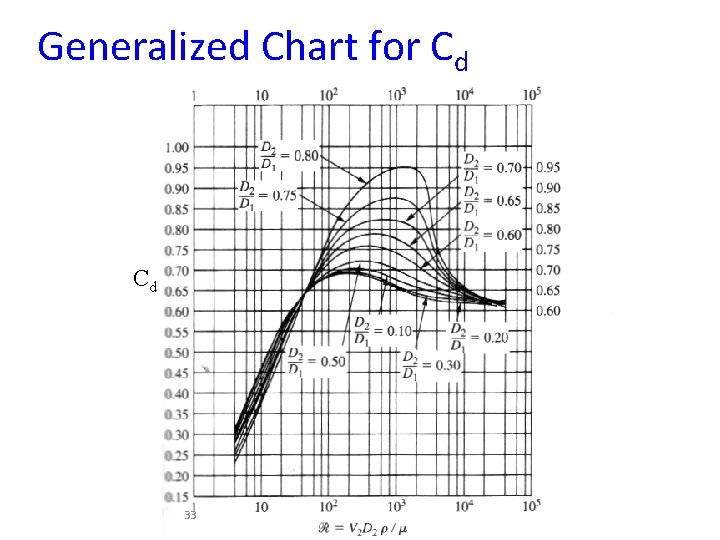
Generalized Chart for Cd Cd 33