Bernoulli Mixture Models for Markov Blanket Filtering and

Bernoulli Mixture Models for Markov Blanket Filtering and Classification Mehreen Saeed Department Computer Science FAST, National University of Computer & Emerging Sciences Lahore Campus, Pakistan Causality challenge workshop IEEE WCCI 2008 June 4, 2008 Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 1

OUTLINE • • • Markov blanket filtering by Koller and Sahami (1996) Mixture models and Bernoulli mixtures Markov blanket filtering using Bernoulli mixtures Results Conclusion Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 2

MARKOV BLANKET FILTERING BY KOLLER AND SAHAMI • Greedy search algorithm for finding the MB of target • Criterion is expected cross entropy • If the above criterion is small then f. G can be used in place of f Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 3

THE ALGORITHM…KOLLER & SAHAMI (1996) 1. 2. Let G = F (entire feature set) Loop a. For each feature Fi G, Let Mi be the features that have highest correlation with Fi F 1 F 2 F 3 … Fd m 11 m 21 m 31 … md 1 m 12 m 22 m 32 … md 2. . . m 1 K m 2 K m 3 K … md. K Mi = Set of features having M 1 M 2 M 3 MK highest correlation with Fi b. Compute G(Fi|Mi) for each i c. Choose the i for which this term is a minimal and define G = G-{Fi} Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 4

BERNOULLI MIXTURES • Model binary data • A single Bernoulli distribution assumes feature independence: • Bernoulli mixtures identify high density data areas on the corners of a hypercube Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 5
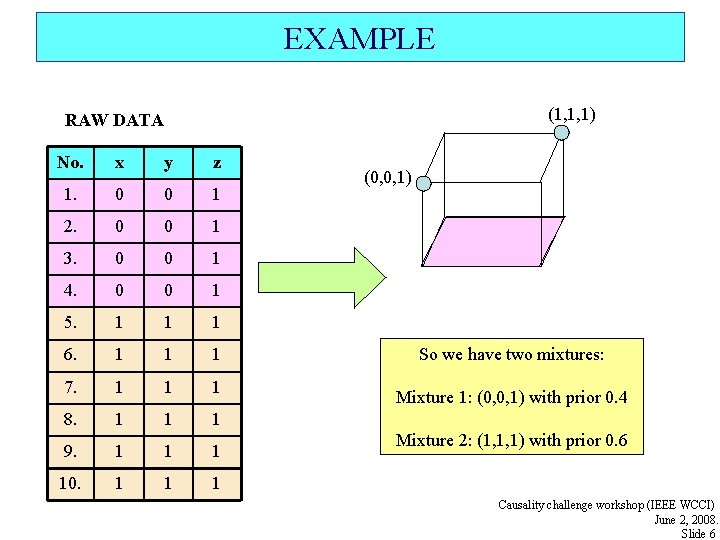
EXAMPLE (1, 1, 1) RAW DATA No. x y z 1. 0 0 1 2. 0 0 1 3. 0 0 1 4. 0 0 1 5. 1 1 1 6. 1 1 1 7. 1 1 1 8. 1 1 1 9. 1 10. 1 1 1 (0, 0, 1) So we have two mixtures: Mixture 1: (0, 0, 1) with prior 0. 4 Mixture 2: (1, 1, 1) with prior 0. 6 Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 6
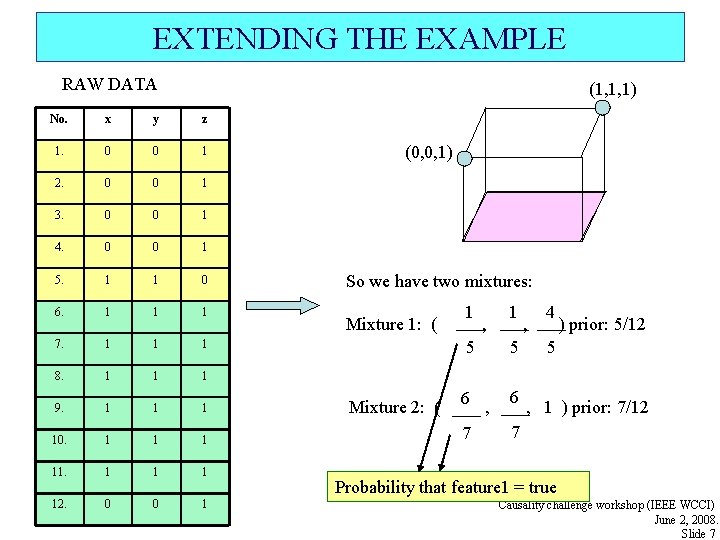
EXTENDING THE EXAMPLE RAW DATA (1, 1, 1) No. x y z 1. 0 0 1 2. 0 0 1 3. 0 0 1 4. 0 0 1 5. 1 1 0 6. 1 1 1 7. 1 1 1 8. 1 1 1 9. 1 10. 1 11. 1 12. 0 0 1 (0, 0, 1) So we have two mixtures: Mixture 1: ( 1 , 5 Mixture 2: ( 6 7 1 5 , 6 , 4 ) prior: 5/12 5 , 1 ) prior: 7/12 7 Probability that feature 1 = true Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 7

BERNOULLI MIXTURES FOR ESTIMATING PROBABILITIES • Feature vector (0. 7, 0. 9, 0. 1) 10% 70% 90% 0 OPTIMISTIC GUESS (1, 1, 0) occurs 70% times 90% 70% 1 PESSIMISTIC GUESS (1, 1, 0) occurs (90 -30 -10 ) 50% times 10% For the current work we used the optimistic guess for feature vector for estimating probabilities Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 8

MODIFY KOLLER & SAHAMI TO USE TRAINING DATA ONLY FOR CALCULATING CROSS ENTROPY • Take all main vectors vi in the mixture models. vi has the features with highest correlation with target 1. 2. 3. 4. 5. Find the probability of vi in +ve class Find the probability of vi in –ve class Calculate P(C|vi) for both +ve and –ve class Similarly calculate P(C|vi , f) Calculate the overall cross entropy DKL(P(C|vi)||P(C|vi, f)) and sum over all feature values and all main vectors. Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 9

GOOD THINGS ABOUT THE ALGO • On SIDO we had 4 Bernoulli mixtures for positive labels and 7 Bernoulli mixtures for negative labels • We used the total 11 mixtures for calculating cross entropy values rather than 12, 678 x 4, 932 matrix • We experimented with large values of K, e. g. , 15, 20, 40… • Not possible with raw data as that can have – Data fragmentation – Computationally very expensive Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 10
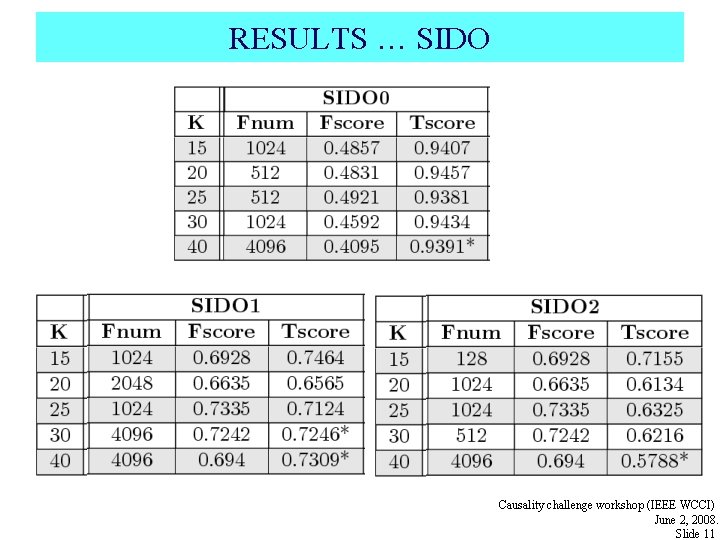
RESULTS … SIDO Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 11
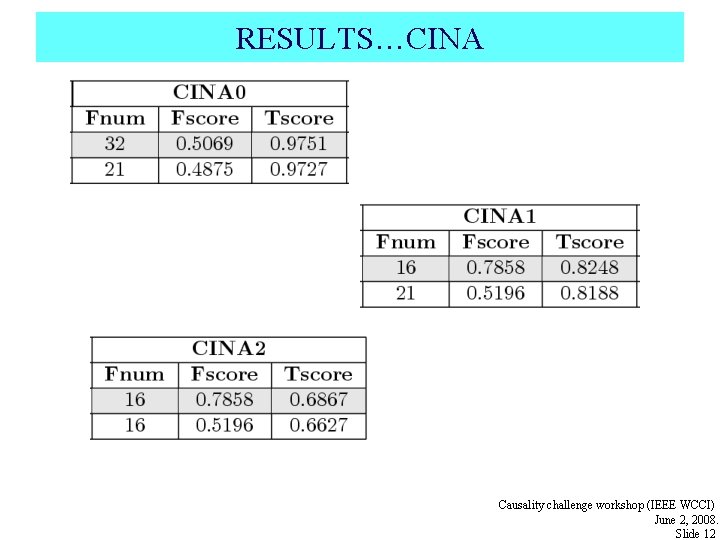
RESULTS…CINA Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 12

ONE LAST NOTE…. ADVISE ON MODEL SELECTION • Don’t ever trust your second thoughts!!! Final entry 1 On second thoughts… Final entry 2 Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 13

CONCLUSIONS • We can use Bernoulli mixtures to get a summary of data • We can discard training data and work with these mixtures • Using Bernoulli mixtures to find cross entropy values is – – – FAST EFFICIENT INTUITIVE SIMPLE EASY to implement Causality challenge workshop (IEEE WCCI) June 2, 2008. Slide 14
- Slides: 14