Benchmarking HFSS and CST eigenmode and CST wake

Benchmarking HFSS and CST eigenmode and CST wake for waveguide damped cavities Alexej Grudiev 6/5/2020

Outline • Motivation • Case 2: Waveguide damped cell with beam pipe • Conclusions • Appendix 1: CST example • Appendix 2: Case 3: Waveguide damped cells with periodic boundary conditions • Appendix 3: Case 1: Pillbox with lossy wall damping

Motivation • Validate HFSS and CST eigenmode solvers for calculation of cavity modes heavily damped by means of waveguides • Example: CLIC accelerating structure, travelling wave periodic structure with few tens of cells like this • There are 4 damping waveguides attached to the cell • The lowest cut off frequency of the damping waveguides (~14 GHz) is above the fundamental accelerating mode frequency 12 GHz, so it is trapped inside • All the HOMs with frequencies above cutoff frequencies of damping waveguide modes are coupled to the waveguides and damped • Damping waveguides are terminated by broadband absorbers which are not considered here but simulated by ideal absorbing boundary condition • This is the subject of the benchmark
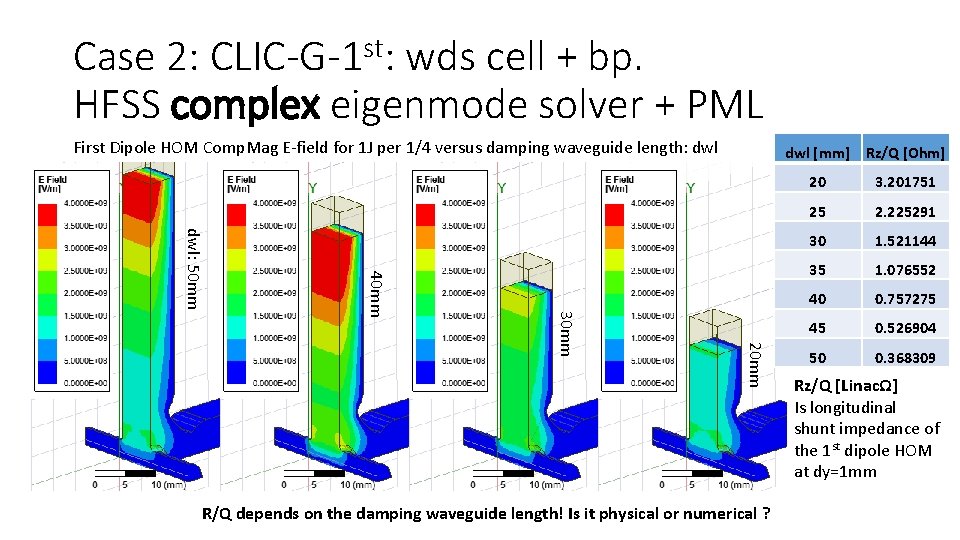
Case 2: CLIC-G-1 st: wds cell + bp. HFSS complex eigenmode solver + PML First Dipole HOM Comp. Mag E-field for 1 J per 1/4 versus damping waveguide length: dwl [mm] Rz/Q [Ohm] 20 mm 30 mm 40 mm dwl: 50 mm R/Q depends on the damping waveguide length! Is it physical or numerical ? 20 3. 201751 25 2. 225291 30 1. 521144 35 1. 076552 40 0. 757275 45 0. 526904 50 0. 368309 Rz/Q [LinacΩ] Is longitudinal shunt impedance of the 1 st dipole HOM at dy=1 mm
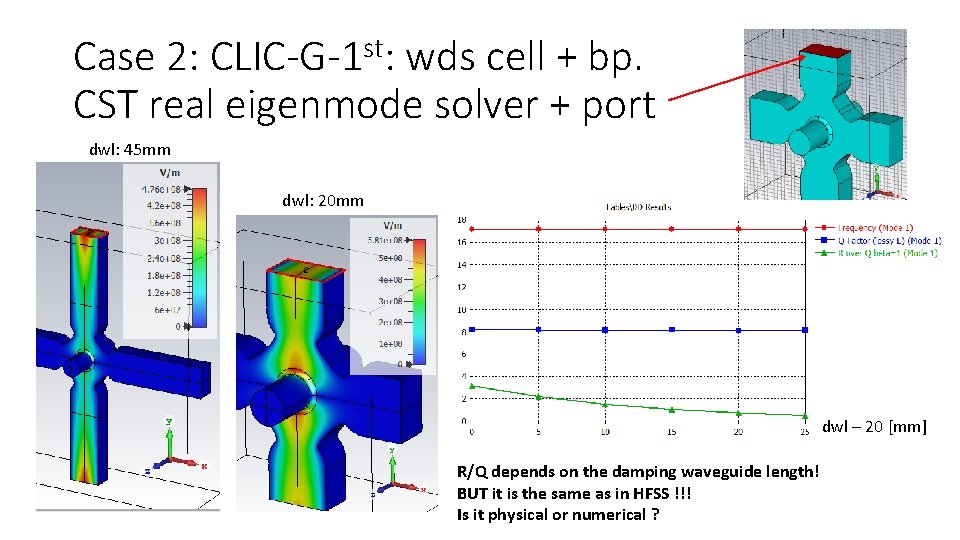
Case 2: CLIC-G-1 st: wds cell + bp. CST real eigenmode solver + port dwl: 45 mm dwl: 20 mm dwl – 20 [mm] R/Q depends on the damping waveguide length! BUT it is the same as in HFSS !!! Is it physical or numerical ?
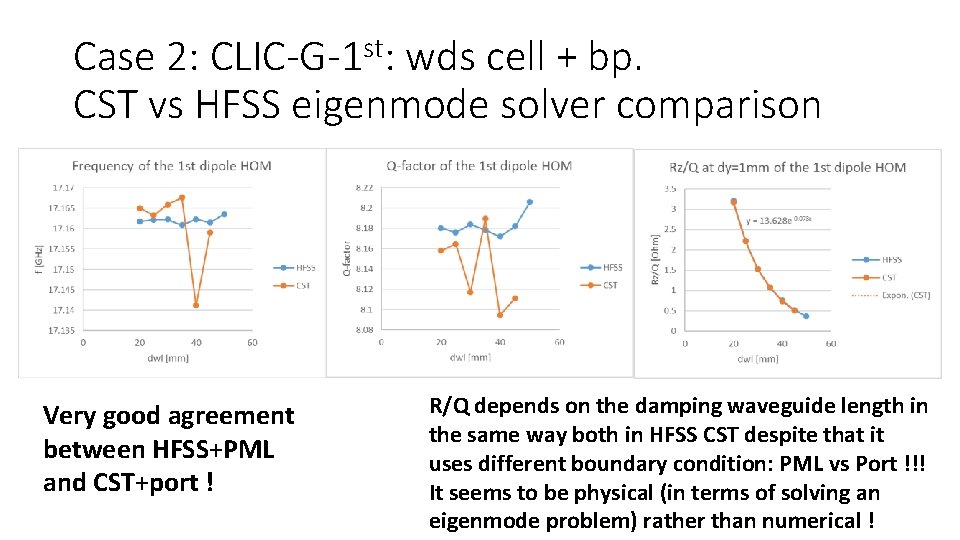
Case 2: CLIC-G-1 st: wds cell + bp. CST vs HFSS eigenmode solver comparison Very good agreement between HFSS+PML and CST+port ! R/Q depends on the damping waveguide length in the same way both in HFSS CST despite that it uses different boundary condition: PML vs Port !!! It seems to be physical (in terms of solving an eigenmode problem) rather than numerical !
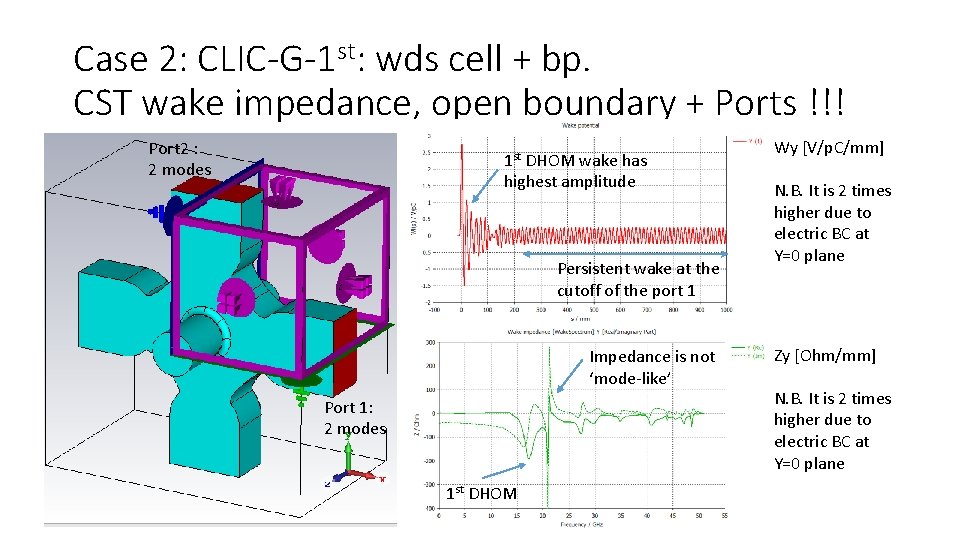
Case 2: CLIC-G-1 st: wds cell + bp. CST wake impedance, open boundary + Ports !!! Port 2 : 2 modes 1 st DHOM wake has highest amplitude Persistent wake at the cutoff of the port 1 Impedance is not ‘mode-like’ Port 1: 2 modes 1 st DHOM Wy [V/p. C/mm] N. B. It is 2 times higher due to electric BC at Y=0 plane Zy [Ohm/mm] N. B. It is 2 times higher due to electric BC at Y=0 plane
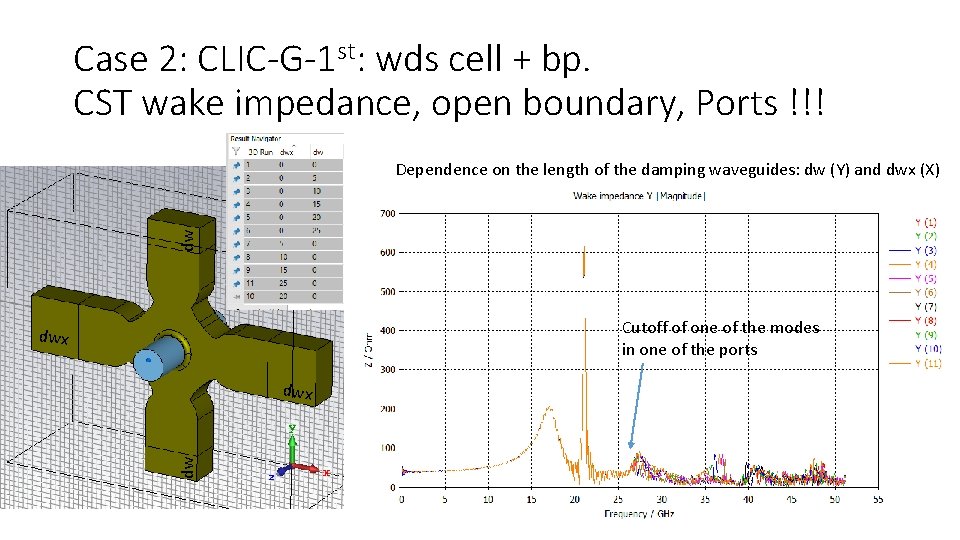
Case 2: CLIC-G-1 st: wds cell + bp. CST wake impedance, open boundary, Ports !!! dw Dependence on the length of the damping waveguides: dw (Y) and dwx (X) Cutoff of one of the modes in one of the ports dwx dw dwx
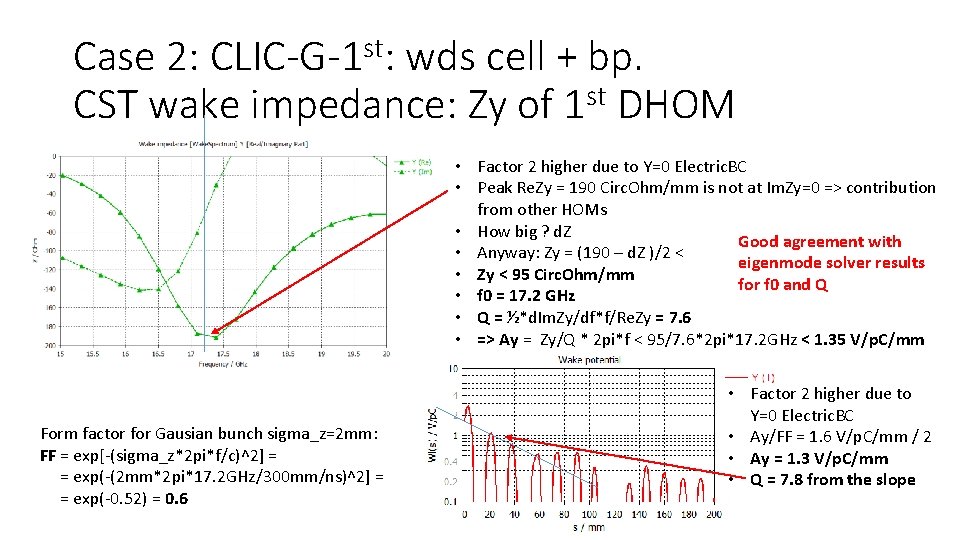
Case 2: CLIC-G-1 st: wds cell + bp. CST wake impedance: Zy of 1 st DHOM • Factor 2 higher due to Y=0 Electric. BC • Peak Re. Zy = 190 Circ. Ohm/mm is not at Im. Zy=0 => contribution from other HOMs • How big ? d. Z Good agreement with • Anyway: Zy = (190 – d. Z )/2 < eigenmode solver results • Zy < 95 Circ. Ohm/mm for f 0 and Q • f 0 = 17. 2 GHz • Q = ½*d. Im. Zy/df*f/Re. Zy = 7. 6 • => Ay = Zy/Q * 2 pi*f < 95/7. 6*2 pi*17. 2 GHz < 1. 35 V/p. C/mm Form factor for Gausian bunch sigma_z=2 mm: FF = exp[-(sigma_z*2 pi*f/c)^2] = = exp(-(2 mm*2 pi*17. 2 GHz/300 mm/ns)^2] = = exp(-0. 52) = 0. 6 • Factor 2 higher due to Y=0 Electric. BC • Ay/FF = 1. 6 V/p. C/mm / 2 • Ay = 1. 3 V/p. C/mm • Q = 7. 8 from the slope

Conclusions Good agreement with all 3 tools Eigenmode solvers cannot give R/Q of waveguide damped cell Wake field solver is needed to get HOM amplitude !!! Frequency and Q-factor can be calculated in eigenmode solver. This is Good enough for the damping design, since amplitude to large extent just a function of aperture which is not affected by damping features. • Damping design must be validated by wakefield solver • • •
Appendix 1: CST example: Loaded Cavity Ext. Q
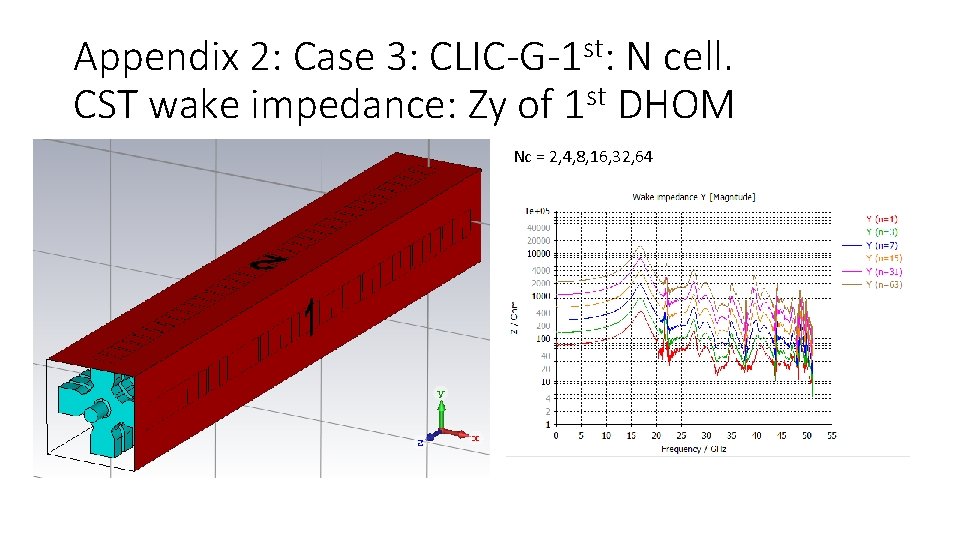
Appendix 2: Case 3: CLIC-G-1 st: N cell. CST wake impedance: Zy of 1 st DHOM Nc = 2, 4, 8, 16, 32, 64
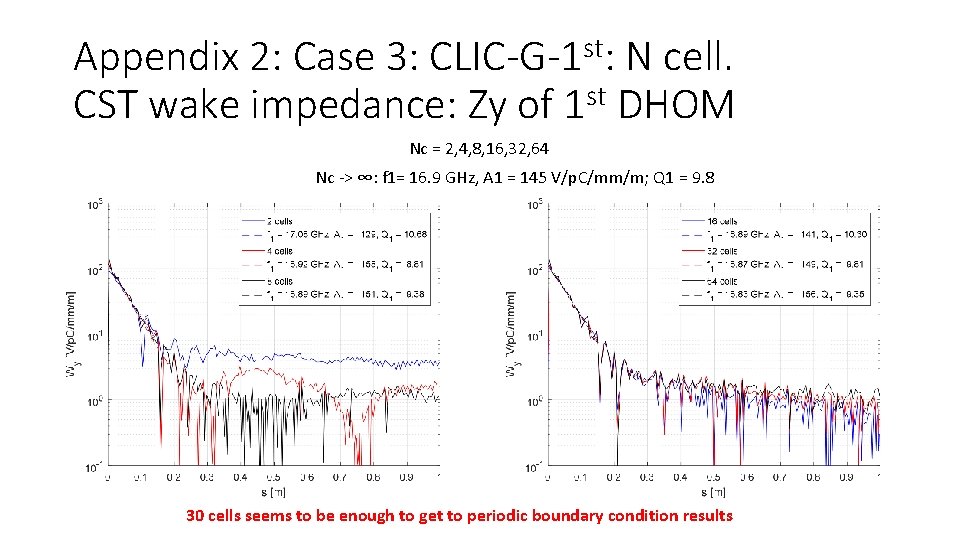
Appendix 2: Case 3: CLIC-G-1 st: N cell. CST wake impedance: Zy of 1 st DHOM Nc = 2, 4, 8, 16, 32, 64 Nc -> ∞: f 1= 16. 9 GHz, A 1 = 145 V/p. C/mm/m; Q 1 = 9. 8 30 cells seems to be enough to get to periodic boundary condition results
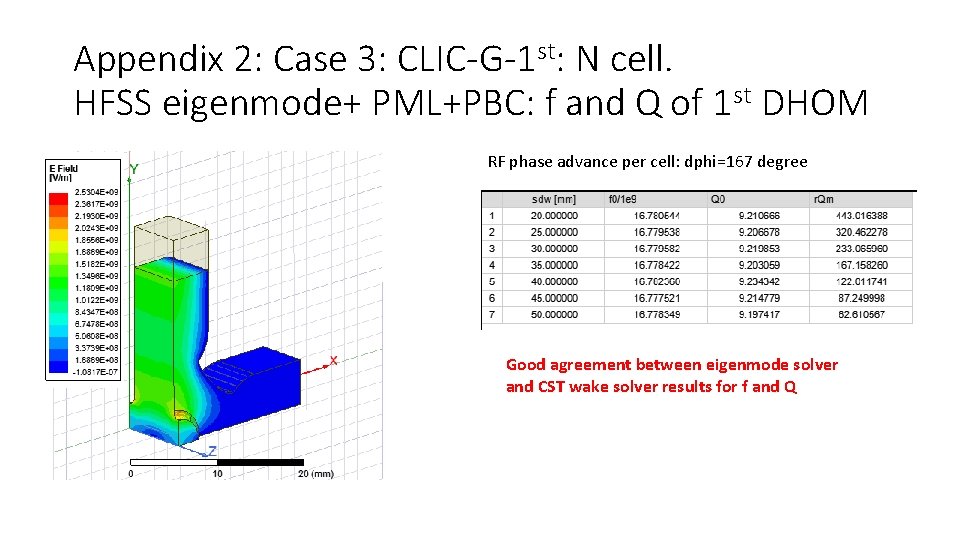
Appendix 2: Case 3: CLIC-G-1 st: N cell. HFSS eigenmode+ PML+PBC: f and Q of 1 st DHOM RF phase advance per cell: dphi=167 degree Good agreement between eigenmode solver and CST wake solver results for f and Q
Appendix 3: Case 1: nds cell + bp + lossy walls. CST real eigenmode solver + perturbation
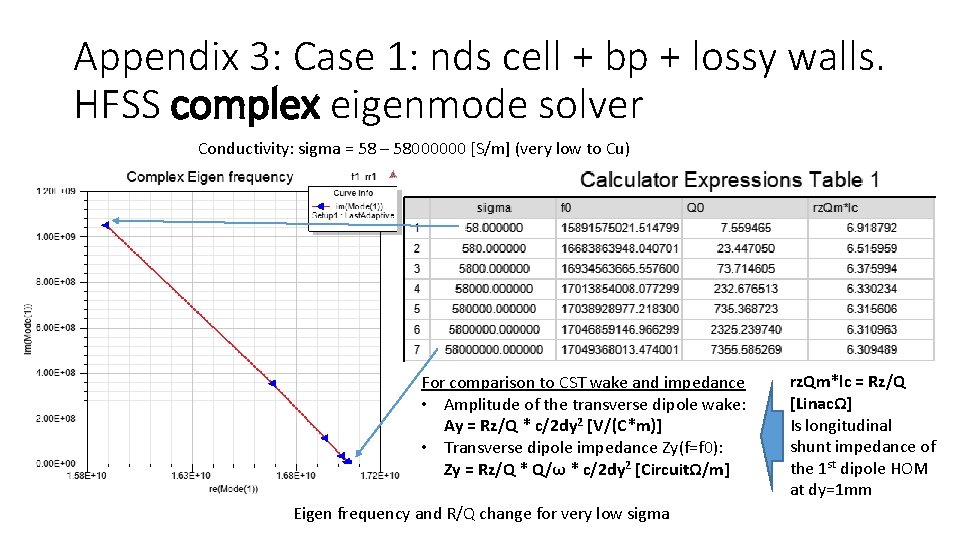
Appendix 3: Case 1: nds cell + bp + lossy walls. HFSS complex eigenmode solver Conductivity: sigma = 58 – 58000000 [S/m] (very low to Cu) For comparison to CST wake and impedance • Amplitude of the transverse dipole wake: Ay = Rz/Q * c/2 dy 2 [V/(C*m)] • Transverse dipole impedance Zy(f=f 0): Zy = Rz/Q * Q/ω * c/2 dy 2 [CircuitΩ/m] Eigen frequency and R/Q change for very low sigma rz. Qm*lc = Rz/Q [LinacΩ] Is longitudinal shunt impedance of the 1 st dipole HOM at dy=1 mm
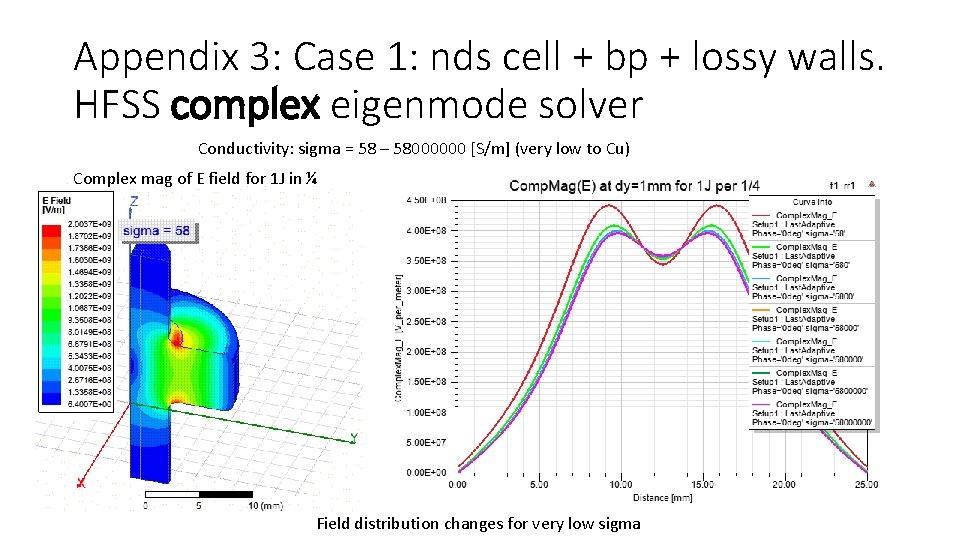
Appendix 3: Case 1: nds cell + bp + lossy walls. HFSS complex eigenmode solver Conductivity: sigma = 58 – 58000000 [S/m] (very low to Cu) Complex mag of E field for 1 J in ¼ Field distribution changes for very low sigma
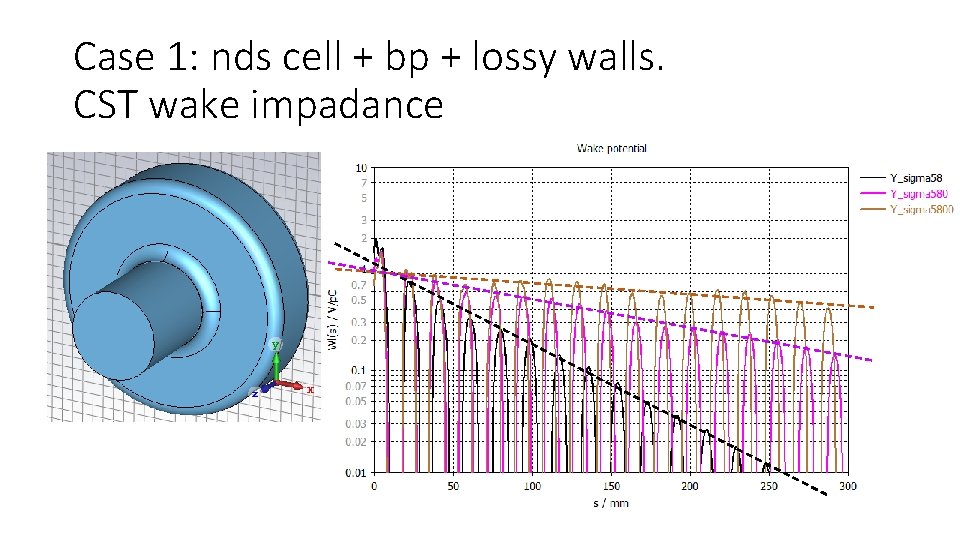
Case 1: nds cell + bp + lossy walls. CST wake impadance
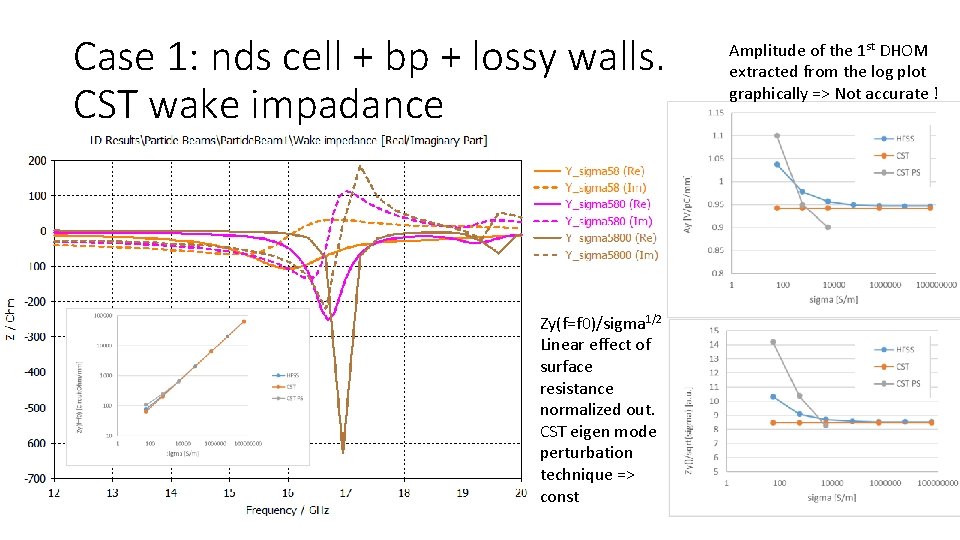
Case 1: nds cell + bp + lossy walls. CST wake impadance Zy(f=f 0)/sigma 1/2 Linear effect of surface resistance normalized out. CST eigen mode perturbation technique => const Amplitude of the 1 st DHOM extracted from the log plot graphically => Not accurate !
- Slides: 19